Файл crc что это
Целостность данных, CRC
Контрольная сумма
И возвращать байт суммы. Создадим и заполним структуру данными и прогоним через эту функцию. В последний байт структуры запишем контрольную сумму:
Теперь можно передать структуру приёмнику! Пример “синтетический”, так как кому и каким способом передавать данные мы не рассматриваем. Хотя, можно отправить по Serial, например с одной Ардуины на другую, как в уроке по парсингу Serial:
Далее на приёмнике примем данные:
Теперь нужно убедиться в том, что данные верны. Для этого прогоним их через ту же суммирующую функцию, но без учёта последнего байта, так как он сам является суммой:
Если значение совпадёт с переданным rxData.hash – данные верны! Дополним предыдущий код:
И по условию можем выполнять какие-то действия, например применить полученные данные к устройству или проигнорировать их. Достоинства контрольной суммы:
Недостатки контрольной суммы:
Низкая надёжность заключается в том, что контрольная сумма не учитывает порядок байтов в посылке, то есть не является уникальным “отпечатком” всех данных. Например, данные повредились так, что из вот такого пакета
Превратились в такой:
CRC (cyclic redundancy code) – циклический избыточный код. Алгоритм тоже выдаёт некое “число” при прохождении через него потока байтов, но учитывает все предыдущие данные при расчёте. Как работает данный алгоритм мы рассматривать не будем, об этом можно почитать на Википедии или здесь. Рассмотрим реализацию CRC 8 бит по стандарту Dallas, он используется в датчиках этой фирмы (например DS18b20 и домофонные ключи iButton). Данная реализация должна работать на всех платформах, так как это чисто C++ без привязки к архитектуре (компилятор сам разберётся):
Финальный пример. Передатчик:
Также коллега поделился реализацией данного алгоритма на ассемблере для AVR, она работает чуть быстрее и весит чуть легче, что может быть критично например для ATtiny:
Функция используется точно так же, как предыдущая.
Методы исправления ошибки в данных CRC
Пользователи регулярно сталкиваются с различными системными сбоями, возникающими по программным или аппаратным причинам. Одной из распространённых проблем является ошибка CRC, сопровождающаяся сообщением с соответствующим текстом «Ошибка данных в CRC». Она свидетельствует о несовпадении контрольных сумм загружаемого файла, что говорит о его изменении или повреждении, и может проявляться при использовании внутренних и внешних накопителей информации. Часто сбой встречается во время записи оптического диска, копирования данных с диска на компьютер, установке игр и приложений или при работе с торрент-клиентами. Момент отслеживания появления сбоя всегда имеет значение, поскольку способ решения проблемы напрямую зависит от того, при каких условиях возникла ошибка CRC.
Что такое CRC
Циклический избыточный код или CRC (англ. Cycle Redundancy Check) является алгоритмом вычисления контрольной суммы файла, используемой для проверки корректности передаваемой информации. То есть в результате обработки информации получается определённое значение, которое обязательно будет разным для файлов, даже на один бит отличающихся между собой. Так, алгоритм, базирующийся на циклическом коде, определяет контрольную сумму и приписывает её к передаваемым данным. В свою очередь принимающая сторона также владеет алгоритмом нахождения контрольной суммы, что даёт возможность системе проверить целостность получаемых данных. Когда эти числа соответствуют, информация передаётся успешно, а при несовпадении значений контрольной суммы возникает ошибка в данных CRC, это означает, что файл, к которому обратилась программа, был изменён или повреждён.
Причины возникновения ошибки CRC
В большинстве случаев проблема носит аппаратный характер, но иногда возникает и по программным причинам. Сообщение «Ошибка данных в CRC» может говорить о неисправности HDD, нарушении файловой системы или наличии битых секторов. Нередко сбой возникает при инициализации жёсткого диска или твердотельного накопителя SSD после подсоединения к компьютеру, несмотря на конструктивные отличия и разницу в способе функционирования, это происходит, поскольку не удаётся правильно прочитать данные. Тогда неполадка может заключаться не только в механических повреждениях, но и в неисправности интерфейсов подключения или плохом контакте. Ошибка в устройствах SSD с интерфейсом PCI-E также случается из-за накопившихся загрязнений на плате. Проблемы с доступом к внешним накопителям нередко связаны с неисправностью портов. Среди программных причин ошибку в данных CRC способны вызывать сбои драйверов устройств. Источником проблемы при установке программного обеспечения посредством торрент-клиента чаще всего является повреждённый архив. Таким образом, можно выделить следующие причины ошибки CRC:
Как исправить ошибку CRC
Факторов, провоцирующих проблему не так уж и мало. Определить источник неприятности чаще всего можно исходя из условий, при которых проявилась ошибка в данных CRC, тогда можно сузить круг возможных причин и понять, как исправить сбой. Все действия, направленные на устранение неисправности будут эффективны в различных ситуациях.
Ошибка в данных CRC при подключении устройства
В случае возникновения проблемы при работе с внешними накопителями прежде, чем лечить устройство посредством специализированных утилит, первым делом следует проверить работу с другими разъёмами. Если порт неисправен, то вопрос может решиться подключением носителя к иному порту на девайсе. Ещё одна причина – плохой контакт, например это часто встречается в адаптере подключения SD карты, а также при использовании устройств HDD или SSD. Флешка, СД карта или другой подключаемый накопитель также могут быть неисправными, для чтения данных с повреждённых устройств используется специальный софт, например, BadCopyPro, но при выходе из строя носителя программные методы бессильны.
Возникновение сбоя при попытке доступа к файлам на HDD
«Ошибка в данных CRC» нередко проявляется по причине нарушения целостности файловой системы или битых секторов на жёстком диске. Поскольку не удаётся правильно прочесть информацию, с этим может быть связан ряд сбоев, включая ситуацию, когда винчестер не инициализируется. Диагностировать HDD можно с помощью встроенных средств Windows или сторонних программ.
Проверка инструментом Chkdsk
В арсенале ОС имеется немало интегрированных служб для решения различных задач. Проверить файловую систему на ошибки, а также обнаружить битые сектора можно с использованием утилиты Check disk, вызываемой из командной строки. Чтобы просканировать жёсткий диск выполняем следующие действия:
В ряде случаев, когда нет доступа ко всему диску или ошибка в данных CRC проявляется при обращении к софту, который раньше работал, сканирование потребуется выполнить в режиме восстановления, для чего потребуется загрузочная флешка или диск с соответствующей ОС Windows. Изменив порядок запуска устройств (выставить в Boot приоритет для съёмного накопителя) и запустившись с загрузочного носителя можно открыть командную строку следующим образом:
Сканирование системной утилитой проверки диска
Можно выполнить проверку на ошибки и другим способом:
При выборе системного диска потребуется запланировать проверку, в таком случае он будет просканирован при следующей загрузке Windows. Для восстановления HDD применяется также сторонний софт, например, HDD Regenerator, Acronis Disk Director, Victoria и прочие. При этом в случае с физическими повреждениями устройства выправить их программно не получится, поэтому лучше заранее скопировать важную информацию с жёсткого диска, возможно, его время уже на исходе.
Проблема при скачивании с CD/DVD носителя
Если ошибка выскакивает при копировании информации с оптического диска на внутренний накопитель, возможно, что диск просто загрязнён или повреждён. Для начала нужно очистить поверхность носителя и попытаться выполнить процедуру снова. Если не помогло, ищем другой источник информации, а при его отсутствии и необходимости восстановления данных с диска можно использовать программу BadCopyPro, которая считывает и возвращает к жизни файлы с испорченных накопителей, если это возможно. К сожалению, при сильно выраженных повреждениях диска скопировать с него файлы не удастся.
Ошибка в данных CRC при записи оптического диска, установке программ или игр
Если проблема возникла в процессе записи образа, скачанного с просторов интернета, на CD/DVD, стоит проверить контрольные суммы записываемых данных перед выполнением процедуры. Для этой цели используется утилита HashTab, после установки которой, в свойствах файла появится новая вкладка «Хеш-суммы файлов», с её помощью вы сможете сравнить значение с исходником. Так, при несовпадении контрольных сумм, следует скачать образ снова.
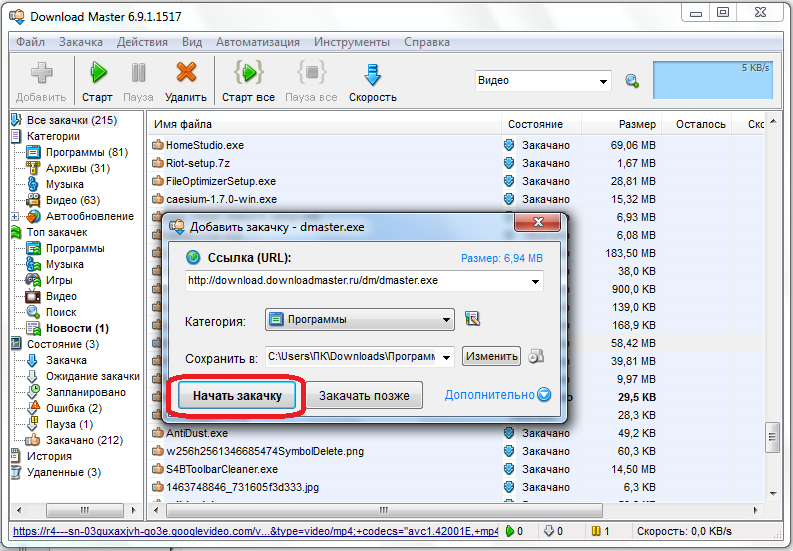
Повторно скачать файл или архив следует также, когда с помощью скачанного дистрибутива программы она не устанавливается на компьютер. Данные могли быть повреждены в процессе загрузки или не были полностью выкачаны. Удобно применять для скачивания uTorrent, поскольку утилита самостоятельно определяет значения контрольных сумм и перекачивает часть информации, загрузившейся с ошибкой. В случае скачивания данных по прямым ссылкам можно использовать Download Master. При этом не исключено, что архив или файл уже был повреждён изначально и в таком виде залит на ресурс, потому нужно попробовать скачать его с альтернативного источника.
Ошибка в uTorrent
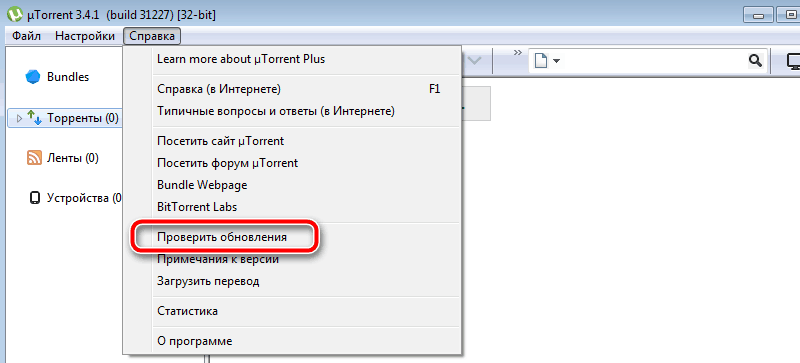
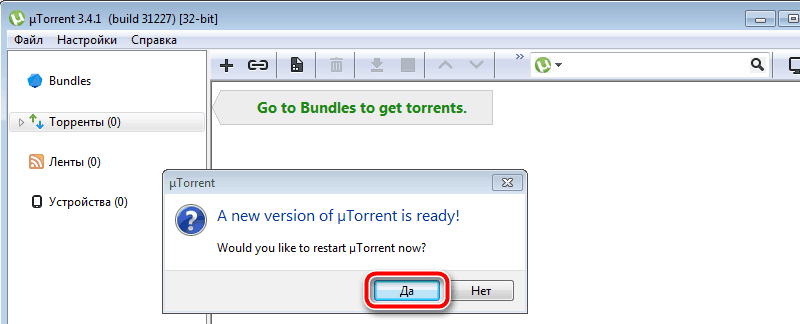
Когда ошибка в данных CRC появляется в программе uTorrent, исправляем её следующими действиями:
Вышеперечисленных способов достаточно, чтобы избавиться от ошибки в данных CRC, возникающей при различных условиях. Так, определив источник появления сбоя, можно целенаправленно устранить проблему. В большинстве случаев исправить ошибку удаётся программными средствами, но, когда речь идёт о физической неисправности накопителя, следует задуматься о его замене.
CRC FAQ. Что, зачем и как
Глава 1. Что такое CRC и зачем он нужен
CRC (cyclic redundancy code) — циклический избыточный код, иногда называемый также контрольным кодом. По своей сути — это просто вычисленное на основе исходного передаваемого сообщения число (или можно сказать код), которое передаётся вместе с самим сообщением (дописывается в конец информационной части) и служит для контроля его безошибочной передачи.
Число это вычисляется по определённым правилам и всегда имеет строго определённое заранее количество разрядов. Очень удобно заранее знать, сколько разрядов занимает контрольное число, потому что иначе станет заранее неизвестной длина сообщения целиком, вместе с CRC, даже при условии, что мы точно знаем длину информационной части. Кроме того, это позволяет заранее выделить для вычисления CRC регистр нужного размера.
Никакой дополнительной информационной нагрузки это число не несёт, поэтому с точки зрения передачи полезной информации оно избыточно. Однако, как я уже сказал, его наличие позволяет диагностировать некоторое количество ошибок, если такие возникают при передаче.
Глава 2. Базовая теория, необходимая для вычисления CRC
По большому счёту, вся теория нахождения CRC базируется на двух вещах.
Первое. Любое сообщение можно представить в виде одного большого двоичного числа и считать что значения разрядов этого числа кодируют коэффициенты некоторого полинома.
Например, возьмём сообщение «15». В шестнадцатиричном виде оно кодируется так: 0x31,0x35. Если перевести эту запись в двоичную форму и записать всё в одну строку, то получим: 00110001 00110101. Если считать, что каждый разряд полученного числа — это коэффициент полинома, то этот полином будет иметь вид:
0*x 15 +0*x 14 +1*x 13 +1*x 12 +0*x 11 +0*x 10 +0*x 9 + 1*x 8 +0*x 7 +0*x 6 +1*x 5 +1*x 4 +0*x 3 +1*x 2 + 0*x 1 +1*x 0
Кратко его можно записать так: x 13 +x 12 +x 8 +x 5 +x 4 +x 2 +1
По большому счёту, мы можем оставить и двоичную запись (чаще всего так и делают, иксы писать неудобно), но будем помнить, что теперь это не просто число, а вектор, составленный из коэффициентов полинома (можно даже продолжать называть такие вектора полиномами). Причём нулевые коэффициенты при старших степенях можно опустить (в дальнейшем вы увидите, что нулевые коэффициенты при старших степенях ни на что не влияют) и написать его в виде 11000100110101.
Второе. Количество разрядов любого двоичного сообщения — это вполне конкретные, конечные числа. Соответственно, множества всех возможных N-разрядных сообщений (где N-любое целое положительное число), составленных по описанному выше способу, — это конечные множества. При использовании особой алгебры такие конечные множества можно считать конечными полями, являющимися расширением простого конечного поля GF(2). Соответственно, любые полиномы, коэффициенты которых составлены из значений разрядов двоичных чисел, можно рассматривать как многочлены над конечным полем.
Подробно многочлены над конечными полями изучаются в отдельном разделе математики, в который мы не будем сильно углубляться в рамках этой статьи. Если кто-то хочет узнать больше — вектор поисков для самостоятельного изучения, я считаю, вполне определён. Нам же интересно, что это за особая алгебра и как это связано с вычислением CRC.
Так вот, отличия этой алгебры от обычной заключаются в следующем:
— операции сложения и вычитания в ней тождественны и выполняются как сложение по модулю 2 (XOR),
— вместо понятий «меньше»/»больше» используются понятия «старше»/»младше». Старшим считается многочлен с большей степенью (наибольшая степень, у которой коэффициент при x равен единице). Например x 3 +1 старше, чем x 2 +x, потому что 3>2.
Нахождение CRC заключается в делении с остатком информационного полинома (тот который составлен из информационного сообщения) на некоторый специальный полином. Делим мы как обычно — столбиком, но вместо операции «вычитания» используем «сложение по модулю 2» и продолжаем деление до тех пор, пока оставшийся в делимом полином не окажется младше полинома делителя. Полученный остаток — это и есть CRC.
Для примера разделим рассмотренный выше полином, составленный из сообщения «15», на полином x 4 +x+1, для чего сначала запишем последний полином со всеми коэффициентами в явном виде (1*x 4 +0*x 3 +0*x 2 +1*x 1 +1*x 0 ), а потом запишем эти коэффициенты в виде вектора (10011). Деление будет выглядеть так, как на рисунке справа.
Нули в самом начале делимого, как я и обещал, нам не пригодились, точно также, как они не пригодились бы нам и при обычном делении.
Идём далее. Что это за специальный полином, на который мы делим наше представленное в виде полинома сообщение?
А это как раз один из основных параметров CRC-алгоритма, называемый также порождающим многочленом или порождающим полиномом. В качестве порождающего многочлена обычно берут какой-либо неприводимый многочлен.
Деление с остатком на полином степени N позволяет получить 2 N различных остатков от деления, причем все эти остатки можно описать N-1 разрядными векторами.
Описанные выше действия — это то, что мы по сути всегда делаем при нахождении CRC. Такое описание алгоритма удобно теоретикам и неудобно инженерам. Поэтому теперь перейдём к частностям, которые приближают нас к практической действительности.
Глава 3. Модификация алгоритма для практического применения.
Посмотрим ещё раз внимательно на наш пример деления столбиком и обратим внимание вот на что — при вычислениях мы фактически всегда оперируем только пятью битами, а могли бы оперировать и четырьмя, поскольку во всех операциях XOR у нас самый старший бит равен единице и он всегда сокращается. То есть, если считать, что вычисления происходят в каком-то выделенном четырёхбитном регистре, то всё деление будет выглядеть так, как будто мы просто на каждом шаге сдвигаем биты в регистре влево, загружая новое значение младшего бита, а старший бит просто выкидываем, если он равен нулю, или, если он равен единице, выполняем XOR регистра и младших четырёх битов порождающего полинома.
То есть теперь можно описать наш алгоритм так: побитно загружаем наше информационное сообщение в регистр нужного размера (на единицу меньше степени порождающего полинома), каждый раз сдвигая регистр влево и помещая новый бит в младший разряд. При этом, если вытесняемый из регистра старший бит равен единице, то выполняем XOR регистра со всеми битами порождающего полинома, кроме старшего. Значение регистра после обработки всего сообщения — это и есть CRC.
На картинке слева тот же самый пример, который мы рассматривали выше, но оформленный в соответствии с новым (инженерным) описанием алгоритма вычисления CRC (хотя по сути, это то же самое деление, что и выше).
Одно отличие в нашем инженерном алгоритме от рассматриваемого выше деления столбиком всё же есть. Отличие это заключается в начальном значении регистра. Мы инициализировали регистр нулями. В итоге наше сообщение стало несколько длиннее первоначального. Как мы знаем, нули в начале сообщения не влияют на результат вычислений, их там можно хоть сколько написать. Но ведь можно инициализировать регистр и не нулями.
Что изменится? Да особенно ничего, просто мы тогда будем искать CRC для несколько модифицированного исходного сообщения (с приписанными в начале битами). Если тот, кто будет определять правильность передачи сообщения, знает об этом и знает какое значение для инициализации регистра нужно выбирать, то он сможет правильно посчитать CRC. Надо сказать, что на практике чаще всего используется инициализация всего регистра нулями или инициализация всего регистра единицами.
Параметры, определяющие формирование битовой последовательности должны описывать:
Наличие последнего параметра связано с тем, что сообщения как правило передаются побайтно и при этом возможны два варианта передачи: старшим битом вперёд (в этом случае биты исходного сообщения располагаются в битовой последовательности, для которой вычисляется CRC, в нормальном порядке) или младшим битом вперёд (в этом случае биты исходного сообщения располагаются в битовой последовательности, для которой вычисляется CRC, в обратном порядке). Причём, иногда переворачивают не только биты в байтах, но и, например, байты в словах. Кстати говоря, во всех примерах, которые приводятся в этой статье, рассматривался только нормальный порядок бит (старшим битом вперёд).
Кроме того, иногда полученный в результате деления остаток дополнительно инвертируют и в качестве CRC используют не сам остаток, а это инвертированное значение.
Помимо описанного в этой статье прямого способа вычисления, существует, так называемый, табличный или быстрый способ расчёта CRC, но об этом как-нибудь в другой раз. А на сегодня, пожалуй, всё.
Как узнать контрольную сумму файла в Windows
При скачивании ISO образов и архивов больших размеров всегда есть вероятность получить «битый» файл. Во времена Dial-UP такое было сплошь и рядом. И хотя сейчас такое случается намного реже, чтобы убедиться, что перед вами «оригинальный» файл придумали контрольные суммы, которые вычисляются на основе содержимого и позволяют заметить несоответствие даже одного байта.
То есть, если вы измените один байт в проверяемом файле, то и контрольная сумма такого файла так же изменится.
Для чего нужны контрольные суммы
У контрольных сумм две задачи:
Зная контрольную сумму оригинала, можно проверить является ли ваша копия подлинной.
Как вычислить контрольную сумму он-лайн
Контрольную сумму можно проверить он-лайн. Но я не буду рекомендовать этот способ, так как если размер вашего файла несколько ГигаБайт, то это займет много времени и всегда есть вероятность ошибки при передаче файла. Кроме того делиться своими файлами со сторонними сервисами не правильно.
Как узнать контрольную сумму файла в Windows
Разумнее вычислить контрольную сумму локально на своем компьютере. Это быстро и конфиденциально. В этой статье я опишу несколько способов получения контрольных сумм, как с помощью сторонних программ, так и непосредственно с помощью самой операционной системы Виндовс.
Файловый менеджер Total Commander
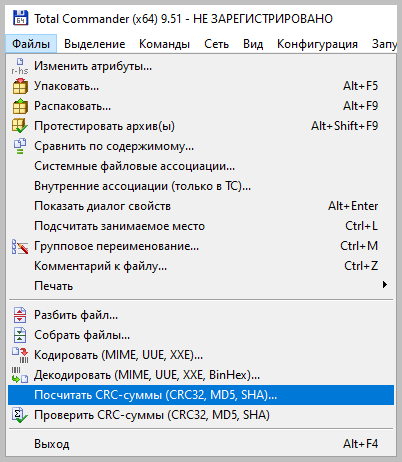
Total Commander — это популярный файловый менеджер, работающий на платформах Microsoft Windows и Android. В нем есть встроенная функция вычисления контрольных сумм.
После чего вы можете выбрать один из алгоритмом вычисления контрольных сумм.
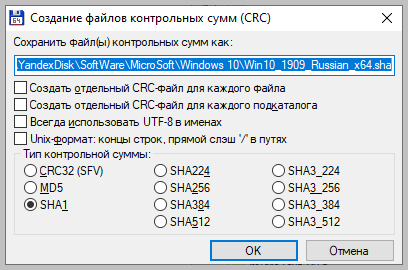
По-умолчанию Total Commander создает файл с именем проверяемого и с расширением по имени выбранного алгоритма расчета контрольной суммы.
Файловый архиватор 7-Zip
7-Zip — свободный, бесплатный файловый архиватор с высокой степенью сжатия данных. Он поддерживает несколько алгоритмов сжатия и множество форматов данных, включая собственный формат 7z c высокоэффективным алгоритмом сжатия LZMA.
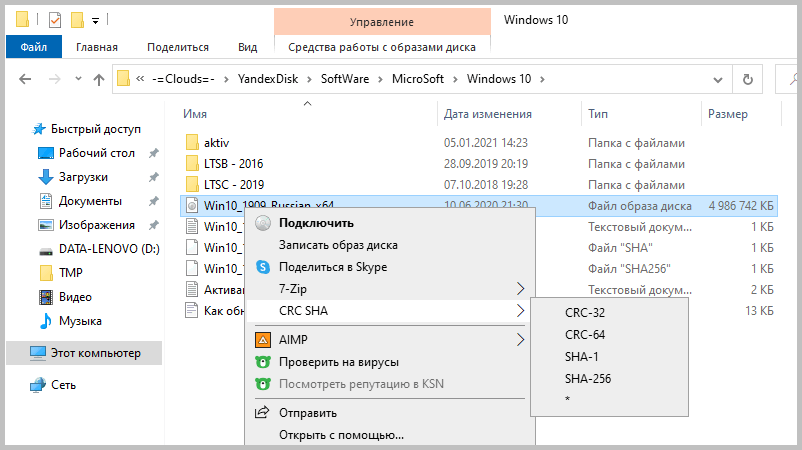
Этот архиватор имеет встроенную функцию вычисления контрольных сумм. Запустить ее можно прямо из контекстного меню Windows:
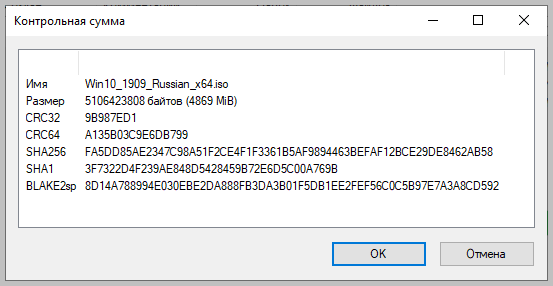
Если выбрать «звездочку», то программа подсчитает сразу несколько контрольных сумм:
Полученные данные можно выделить и скопировать в текстовый документ.
Как подсчитать контрольную сумму файла из консоли Windows
Чтобы посчитать контрольную сумму совсем не обязательно устанавливать специальные программы. И если вы не пользуетесь упомянутыми выше, то можете рассчитать контрольную сумму прямо из командной строки операционной системы.
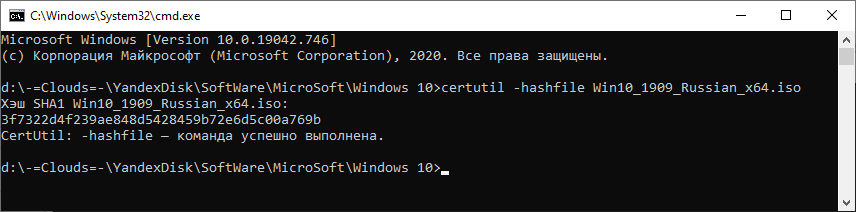
Например, чтобы посчитать контрольную сумму SHA1 с помощью утилиты CertUtil нужно запустить командную строку Windows 10, 8 или Windows 7 и ввести следующую команду:
Вот пример ее работы через несколько минут:
Считаем контрольную сумму в PowerShell
PowerShell — это средство автоматизации от Microsoft, с интерфейсом командной строки и языка сценариев, работает и включена в состав Windows 8 и новее.
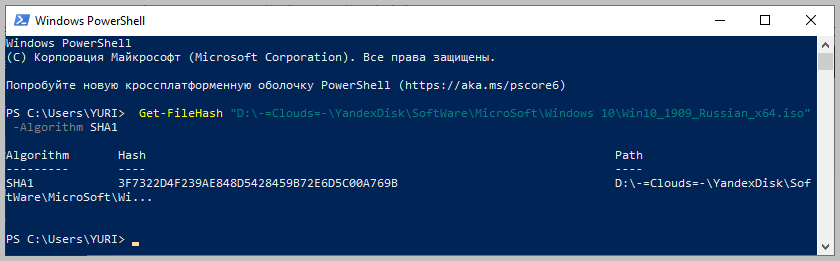
Чтобы вычислить контрольную сумму файла необходимо выполнить команду Get-FileHash указав через пробел имя файла и алгоритм вычисления контрольной суммы:
Обратите внимание, что полный путь и имя файла лучше заключить в двойные кавычки.
По-умолчанию, если не указать тип контрольной суммы, то будет посчитана SHA-256.
Для алгоритмов вычисления контрольной суммы в Windows PowerShell поддерживаются следующие значения:
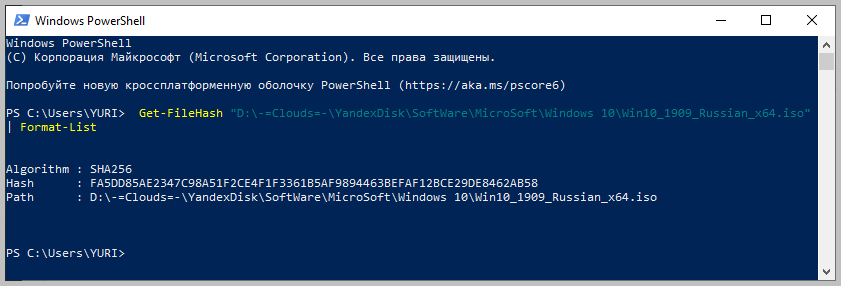
Для оформления вывода в виде списка можно использовать параметр | Format-List. Например:
Тогда результат работы будет выглядеть так:
Подробнее об использовании команды Get-FileHash можно прочитать на официальном сайте Microsoft — https://docs.microsoft.com/ru-ru/powershell/module/microsoft.powershell.utility/get-filehash
Какой алгоритм вычисления контрольных сумм самый правильный
MD5, SHA-1, SHA-256 и прочие – это разные алгоритмы хеш-функции. Хэши являются результатом работы криптографических алгоритмов, и представляют собой строку символов. Часто эти строки имеют фиксированную длину, независимо от размера входных данных.
MD5 самый быстрый, считается устаревшим, а SHA-256 имеет наименьшую вероятность коллизии, когда два разных файла имеют одинаковую контрольную сумму.
Для проверки целостности файла вам следует использовать тот, который предоставляет издатель. Если у вас на выбор есть несколько контрольных сумм, то лучше выбрать в следующей последовательности MD5, SHA-1, SHA-256, последний вариант является более предпочтительным.
Выводы
Если вы сомневаетесь в целостности скаченных файлов из интернета, особенно когда это касается оригинальных образов операционных систем, то проверьте их контрольную сумму. Сделать это можно как с помощью уже имеющихся у вас программ, так и воспользовавшись встроенными средствами операционной системы Windows.