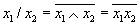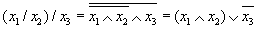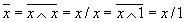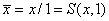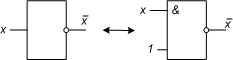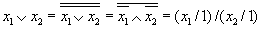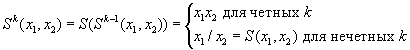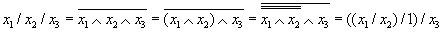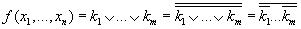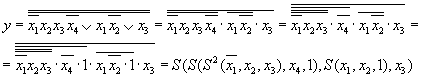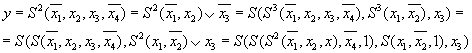что означает бинарная логическая операция штрих шеффера
Штрих Шеффера
Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 г. (в отдельных источниках именуется как Пунктир Чулкова)
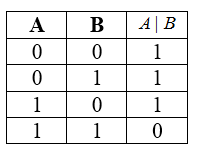
Штрих Шеффера, обычно обозначаемый |, задаётся следующей таблицей истинности:
| X | Y | X|Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Таким образом, высказывание X | Y означает, что X и Y несовместны, т.е. не являются истинными одновременно. От перемены мест операндов результат операции не изменяется.
Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть используя только штрих Шеффера можно построить остальные операции. Например,
— отрицание 
— дизъюнкция 
— конъюнкция 
— константа 1
В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная 155 серия.
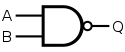
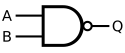
Элемент, реализующий штрих Шеффера обозначается следующим образом (по стандартам ANSI):
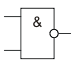
В европейских стандартах принято другое обозначение:
См. также
Литература
Полезное
Смотреть что такое «Штрих Шеффера» в других словарях:
ШЕФФЕРА ШТРИХ — логическая операция, обычно обозначаемая |, к рая задается следующей истинностной таблицей: Таким образом, высказывание означает, что Аи Внесовместны, т. е. не являются истинными одновременно. Через Ш. ш. выражаются все другие логич. операции.… … Математическая энциклопедия
Аксиома Вольфрама — является результатом исследований, осуществленных Стивеном Вольфрамом[1] в поиске кратчайшей аксиомы из одного уравнения, эквивалентной аксиомам булевой алгебры (или логике высказываний). Результатом[2] его поиска стала аксиома с шестью… … Википедия
Булева функция — В данной статье или разделе имеется список источников или внешних ссылок, но источники отдельных утверждений остаются неясными из за отсутствия сносок … Википедия
ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия
Логические операции — логические связки, логические операторы, функции, преобразующие высказывания или пропозициональные формы (т. е. выражения логики предикатов (См. Логика предикатов), содержащие переменные (См. Переменная) и обращающиеся в высказывания при… … Большая советская энциклопедия
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
Стрелка Пирса — Стрелка Пирса бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880 1881 г.г. Стрелка Пирса, обычно обозначаемая ↓, задаётся следующей таблицей истинности:… … Википедия
Логические элементы — Логические элементы устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого «1» и низкого «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике,… … Википедия
Битовая операция — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
Булевы операции — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
Штрих Шеффера
Из Википедии — свободной энциклопедии
Штрих Шеффера, обычно обозначаемый | или ↑, эквивалентен операции И-НЕ [1] и задаётся следующей таблицей истинности:
| X | Y | X | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Таким образом, высказывание X | Y означает, что X и Y несовместны, то есть не являются истинными одновременно. От перемены мест операндов результат операции не изменяется.
Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть, используя только штрих Шеффера, можно построить остальные операции. Например,
В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная 155 серия.
Элемент 2И-НЕ (2-in NAND), реализующий штрих Шеффера, обозначается следующим образом (по стандартам ANSI):
В европейских стандартах принято другое обозначение:
Логические операции и их свойства
Вы будете перенаправлены на Автор24
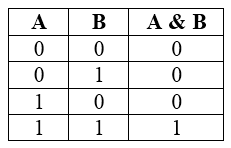
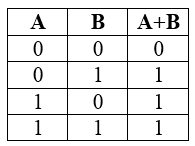
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Таблица истинности для конъюнкции
Дизъюнкция или логическое сложение (в теории множеств это объединение)
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Таблица истинности для дизъюнкции
Готовые работы на аналогичную тему
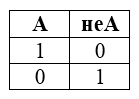
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Таблица истинности для инверсии
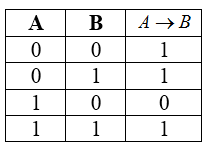
Импликация или логическое следование
Таблица истинности для импликации
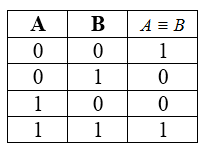
Эквивалентность или логическая равнозначность
Таблица истинности для эквивалентности
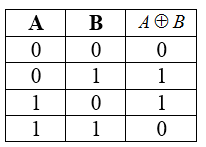
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Таблица истинности для операции сложения по модулю два
Свойства строгой дизъюнкции:
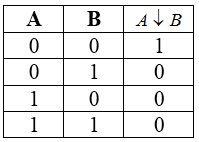
Стрелка Пирса
Таблица истинности для стрелки Пирса
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X \downarrow X = ¬X$— отрицание
$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция
$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция
$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Таблицей истинности для функции штрих Шеффера
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X \mid X = ¬X$ — отрицание
$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция
$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Общие свойства
СОДЕРЖАНИЕ
Определение
Таблица истинности
Логические эквивалентности
История
Чарльз Сандерс Пирс (1880 г.) открыл функциональную полноту NAND или NOR более 30 лет назад, используя термин ampheck (для «разрезания в обе стороны»), но он так и не опубликовал свое открытие.
Характеристики
Другие логические операции в терминах штриха Шеффера
Формальная система на основе мазка Шеффера
Ниже приводится пример формальной системы, полностью основанной на мазке Шеффера, но обладающей функциональной выразительностью логики высказываний :
Символы
Синтаксис
Правило построения I. Для каждого натурального числа n символ p n представляет собой правильно построенную формулу (wff), называемую атомом.
Правило закрытия: любые формулы, которые не могут быть построены с помощью первых двух правил построения, не являются wffs.
Процедура принятия решения для определения того, правильно ли сформирована формула, выглядит следующим образом: «деконструируйте» формулу, применяя Правила построения в обратном порядке, тем самым разбивая формулу на более мелкие подформулы. Затем повторите этот рекурсивный процесс деконструкции для каждой подформулы. В конце концов, формула должна быть сокращена до ее атомов, но если некоторая подформула не может быть сокращена таким образом, то формула не является wff.
Исчисление
Упрощение
Поскольку единственной связкой этой логики является |, символ | можно вообще отбросить, оставив только круглые скобки для группировки букв. Пара круглых скобок всегда должна заключать пару wff s. Примеры теорем в этих упрощенных обозначениях:
Обозначения можно упростить, если
Это следует тем же правилам, что и версия с круглыми скобками, с заменой открывающей скобки чертой Шеффера и удалением (лишней) закрывающей скобки.
Что означает бинарная логическая операция штрих шеффера
8.4.3. РЕАЛИЗАЦИЯ ФУНКЦИЙ В УНИВЕРСАЛЬНЫХ БАЗИСАХ
Логические или комбинационные схемы, являющиеся основой для построения различных вычислительных устройств и компьютеров, обычно строят из логических элементов (ЛЭ), каждый из которых реализует определенную переключательную функцию. При изготовлении ЛЭ, а также при построении БИС выгодно иметь один тип элементов, которые могут быть использованы для построения любой логической схемы. Такой логический элемент должен быть универсальным. Он должен обеспечивать возможность построения схемы для любой переключательной функции.
Подобные ЛЭ, как правило, реализуют переключательные функции, зависящие от небольшого числа аргументов (2-8), поэтому при построении логических схем, описываемых сложными переключательными функциями, приходится использовать суперпозицию переключательных функций, реализуемых ЛЭ. В логической схеме суперпозиции функций соответствует каскадное соединение ЛЭ.
Для упрощения перехода от переключательной функции к реализующей ее логической схеме переключательную функцию удобно записывать в так называемой операторной форме, в которой каждый использованный оператор F(x1. xk) реализует функцию φ(x1. xk) и однозначно соответствует некоторому ЛЭ с входами и одним выходом в логической схеме.
8.4.3.1. Построение логических схем из элементов Шеффера
В качестве первого универсального базиса рассмотрим базис В= – “Штрих Шеффера” (отрицание конъюнкции):
Для перехода к логическойсхеме введем оператор S(x1, x2) = x1 / x2, которому соответствует универсальный элемент Шеффера (рис. 8.36),где “↔“ – символ соответствия:
| S(x1, x2) | ↔ |  |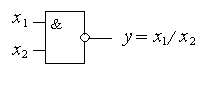
Доказательство.
Приведем к ДНФ обе части равенства:
Полученные в результате преобразований формулы не эквивалентны, что доказывает неассоциативность операции «Штрих Шеффера».
Выразим теперь функции базиса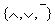 
через функцию » / «.
Инверсия: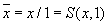 
. В дальнейшем будем использовать второй из рассмотренных способов инвертирования, заменяя все неиспользуемые аргументы константой 1.
Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Шеффера ( рис. 8.37 ):
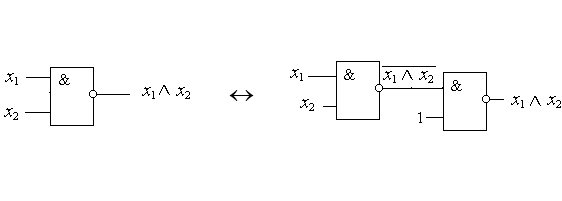
Конъюнкция: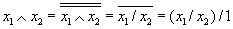
.
Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Шеффера (рис. 8.38):
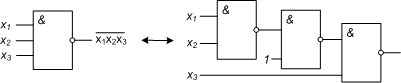
Аналогично можно определить оператор произвольной степени:
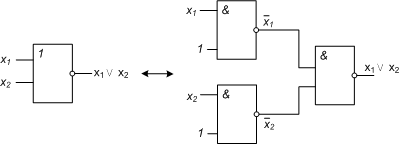
Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Шеффера(рис.8.39).
По аналогии с операциями конъюнкции и дизъюнкции можно рассматривать как обобщение двуместнойоперации «/» многоместную операцию «Штрих Шеффера» и многоместный оператор Шеффера:
где t – местность оператора и соответственно число входов многовходового универсального логического элемента Шеффера. Следует, однако,соблюдатьосторожностьприпопыткепредставить многоместнуюоперацию «Штрих Шеффера» в виде суперпозиции операций Шеффера меньшей местности. Следует помнить, что операция «/» не ассоциативна, поэтому, например, не справедливы равенства:
Эквивалентное преобразование имеет вид:
и может быть проиллюстрировано фрагментами логических схем(рис. 8.40):
Способ 1.
ШАГ 1. Произвольную формулу с помощью эквивалентных преобразований по законам булевой алгебры вначале привести к ДНФ. Затем к ДНФ применять закон двойного отрицания и закон де Моргана для перехода в базис Шеффера:
ШАГ 2. Если какие-либо операции Шеффера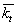 
(отрицание конъюнкции) в полученной записи имеют местность больше t, необходимо выразить их через операции местности. Операции с местностью меньше t следует привести к необходимой местности, заменяя отсутствующие переменные константой 1.
ШАГ 3. Заменить каждую операцию Шеффера местностью t соответствующим оператором Шеффера, построить логическую схему.
Примечание:
Вырожденной (однобуквенной) конъюнкции вида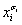 
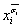
в ДНФ вновой формуле соответствует вырожденная (однобуквенная) операция Шеффера вида 
.
Пример 4.1.
Пусть исходной является формула в ДНФ.
и t = 3
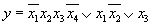
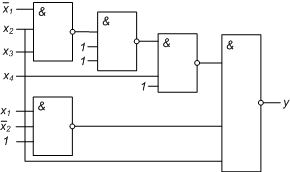
По операторному представлению легко построить логическую схему (рис 8.41 ).
Способ 2.
Произвольная формула над базисом 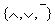приводится к новому виду последовательной заменой операций исходного базиса эквивалентными подформулами в новом базисе в операторной форме. После этого понижаются степени операторов 3 и выше.
Примечание:
Вначале следует использовать операторы Шеффера произвольной местности, а затем привести их к необходимому значению t.
Пример 4.2.
Пусть исходной является формула в ДНФ.
и t = 3
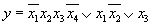
Соответствующая логическая схема аналогична приведенной на рис. 8.41.
Пред.Страница След.Страница Раздел Содержание