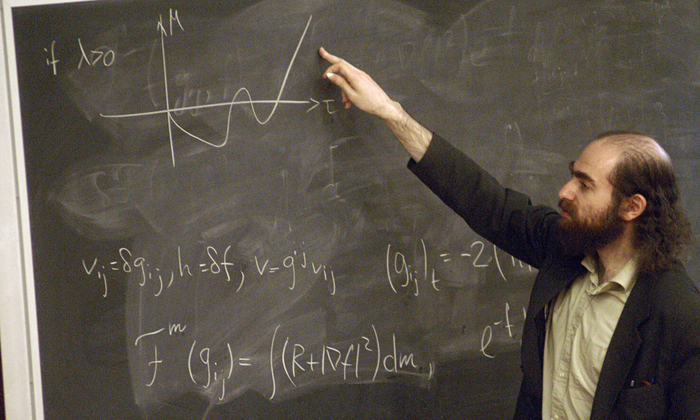что означает гипотеза пуанкаре
Гипотеза Пуанкаре
Гипотеза Пуанкаре — это доказанная гипотеза о том, что если трёхмерная поверхность чем-то похожа на сферу, и если её расправить, она превратится именно в сферу.
Одна из версий официальной формулировки гипотезы Пуанкаре́ звучит так: «Всякое связное, односвязное, компактное трёхмерное многообразие без края гомеоморфно сфере S³».
Гипотеза Пуанкаре была сформулирована в 1904 году известным французским математиком Анри Пуанкаре. В 2002–2003 годах она была доказана русским математиком Григорием Перельманом. После этого Гипотеза Пуанкаре стала именоваться теоремой Пуанкаре — Перельман.
Топология — простыми словами это «геометрия резинового листа» или «резиновая геометрия» т.к. объекты растягиваются и сжимаются как резина и их невозможно сломать; топология изучает свойства пространств, которые неизменны под давлением любой непрерывной деформации. Гипотеза Пуанкаре связана с топологией.
Доказательство
Простыми словами: Перельман доказал при помощи потока Риччи, что при эволюции любая замкнутая кривая на плоскости ведёт себя одинаково и превращается в окружность.
В своих статьях, где Перельман опубликовал идеи доказательства, он также доказал гипотезу о геометризации Уильяма Тёрстона, частным случаем которой является гипотеза Пуанкаре.
Гипотеза геометризации Уильяма Тёрстона гласит, что каждое трёхмерное многообразие локально изометрично только одному из восьми различных типов (изометрично — в науке это то, что относится к равенству меры или этим характеризуется).
Доказательство Перельмана было основано на теории потока Риччи и использовало результаты Чигера, Громова и самого Перельмана о метрических пространствах.
Метрическое пространство — это набор, где есть функция измерения расстояния между точками и который называется метрикой.
Что доказательство гипотезы дало науке?
В плане астрономии эта теорема предполагает, что если наша Вселенная имеет характеристики односвязного компактного многообразия без края, следовательно, она является трёхмерной сферой. Однако ранее считалось, что Вселенная является бесконечной (т.е. имеет форму евклидового трёхмерного пространства).
Теорема Перельмана — Пуанкаре также имеет огромное значение для математики, особенно способ её доказательства. Эта теорема считается математической формулой Вселенной. Она описывает наш мир, который является гладким трёхмерным многообразием.
Что доказывает теорема Пуанкаре о возвращении
Все началось еще в конце XIX века, когда ученый из Франции, Анри Пуанкаре, изучал различные части систем, которые могут быть полностью проанализированы. Как обычно, звучит это не так сложно, но именно его труды легли в основу большой задачи и стали одной из загадок, которую ученые современности называют ”Задачами тысячелетия”. Думаю вы легко согласитесь, что если подождать достаточное количество времени, то планеты в небе выстроятся в нужную вам линию. Так же будет и с частицами газа или жидкости, которые могут сколько угодно менять свое положение, но теоретически в один из моментов времени выстроятся относительно друг друга так, как они располагались в момент начала измерений. На словах все просто — рано или поздно это случится, иначе быть не может. Вот только на деле доказать это довольно сложно. Именно над этим и работал Анри Пуанкаре больше века назад. Позже его теории были доказаны, но от этого не стали менее интересными.
Теорий, гипотез, теорем и просто рассуждений очень много. Все их надо доказывать.
Кто такой Анри Пуанкаре
Жюль Анри Пуанкаре (фр. Jules Henri Poincaré) родился 29 апреля 1854 в Нанси, Франция, а умер 17 июля 1912 в Париже, Франция. Он был французским ученым, в сферу интересов которого входили самые разные науки. Среди них были: математика, механика, физика, астрономия и философия.
Кроме того, что он занимался исследованиями, Анри Пуанкаре в разные годы также был главой Парижской академии наук, членом Французской академии и ещё более 30 академий мира, в том числе иностранным членом-корреспондентом Петербургской академии наук.
Физики зафиксировали квантовый шум в лаборатории LIGO – что нужно знать?
Чуть ли не единогласно историки называют Анри Пуанкаре одним из величайших математиков всех времён. Его ставили в один ряд с Гильбертом, последним математиком-универсалом, учёным, способным охватить все математические результаты своего времени.
Анри Пуанкаре сделал для математики настолько много, что некотрые его труды до сих пор приносят нам пользу.
Перу Анри Пуанкаре принадлежат более 500 статей и книг. Все это говорит о нем, как о гении, который даже спустя более 100 лет после своей смерти может изменить мир будущего своими теориями, формулами, рассуждениями и прочими научными трудами.
Что такое теорема возвращения Пуанкаре
Теорема Пуанкаре о возвращении — одна из базовых теорий эргодической теории. Её суть в том, что при сохраняющем меру отображении пространства на себя почти каждая точка вернётся в свою начальную окрестность. На это потребуется огромное, но конечное количество времени.
С одной стороны, все логично, но есть у данной теории и немного непонятное следствие. Например, у нас есть сосуд, который разделен перегородкой на два отсека. В одном находится газ, а во втором ничего. Если убрать перегородку, то газ заполнит собой весь сосуд. Если верить теории повторения, то рано или поздно все частицы газа должны выстроиться в изначальной последовательности в половине сосуда.
Немного развязывает руки то, что время, которое на это потребуется, может быть очень большим. Но такое следствие не совсем корректно, так как изменились условия наблюдения. Зато, если говорить о том, что перегородку мы убирать не будем, объем газа не изменится и ему не придется нарушать законы физики, произвольно меняя свою плотность, и частицы газа рано или поздно действительно займут те места, в которых они были на момент начала наблюдений.
Есть такие загадки науки, которые были понятны гению, но после него никто так и не может этого доказать. Хотя, все понимают, что автор был прав.
Теория Пуанкаре в квантовой системе
Если мы говорим о том, что в традиционной системе повторения возможны и даже неизбежны, то можно предположить, что в квантовой системе, в которой возможны несколько состояний, все немного иначе. Оказывается, это не так, и труды Пуанкаре могут быть применены и к квантовым системам. Однако правила будут немного иными.
Проблема применения заключаются в том, что состояние квантовой системы, которая состоит из большого количества частиц, не может быть измерено с большой точностью, не говоря уже об идеальном измерении. Более того, можно сказать, что частицы в таких системах можно рассматривать в качестве полностью независимых объектов. Учитывая запутанности, не сложно понять, что при анализе таких систем придется столкнуться с большим количеством сложностей.
Несмотря на это, ученые не были бы учеными, если бы не попытались продемонстрировать эффект повторения Пуанкаре в том числе и в квантовых системах. Сделать это у них получилось. Вот только пока это возможно только для систем с очень небольшим числом частиц. Их состояние нужно измерить как можно точнее и обязательно учесть его.
Сказать, что сделать это сложно — ничего не сказать. Главная сложность в том, что время, которое потребуется системе для возвращения в исходное состояние, будет очень сильно возрастать даже при незначительном увеличении количества частиц. Именно поэтому некоторые ученые анализируют не систему в целом, а ее отдельные частицы. Они пытаются понять, возможно ли возвращение к первоначальному значению некоторых участков этой системы.
Для этого они изучают и анализируют поведение ультрахолодного газа. Он состоит из тысяч атомов и удерживается на месте при помощи электромагнитных полей. Описать характеристики подобного квантового газа можно несколькими величинами. Они говорят о том, насколько тесно могут быть связаны частицы с помощью эффектов квантовой механики. В обычной жизни это не так важно и может даже показаться чем-то ненужным, но в квантовой механике это имеет решающее значение.
В итоге, если понять, как такие величины характеризуют систему в целом, можно будет говорить о возможности квантового возвращения. Получив такие знания, можно более смело говорить о том, что мы знаем, что такое газ, какие процессы в нем происходят и даже прогнозировать последствия воздействия на него.
Квантовые системы сильно отличаются от всего, что мы можем себе представить.
В последнее время ученые смогли доказать, что квантовые состояния могут возвращаться, но некоторые поправки в концепцию повторения внести все же стоит. Не стоит пытаться измерить всю квантовую систему в целом, ведь эта задача близка к невозможности. Куда правильнее будет сосредоточиться на некоторых ее элементах, которые можно измерить и предсказать поведение системы в целом.
Если сказать более смело, то такие исследования и наработки в сфере самых разных наук приближают создание настоящего квантового компьютера, а не тех тестовых систем, которые существуют сейчас. Если дело продвинется, то нас ждет большое будущее. А сначала казалось, что это просто измерение чего-то непонятного. Не так ли?
Проблемы 2000 года: гипотеза Пуанкаре
Проблема, о которой пойдет речь сегодня, выбивается из ряда других проблем 2000 года: лишь она одна считается уже решенной.
Введение
Анри Пуанкаре
За свою жизнь Анри Пуанкаре успел поработать во многих областях науки: комплексном анализе, небесной механике, алгебраической геометрии, теории чисел и, конечно, топологии, в которой он и сформулировал носящую его имя гипотезу. Не все знают, что Пуанкаре стоял у истоков теории относительности: долгое время он сотрудничал с Хендриком Лоренцом (кстати, преобразования Лоренца получили имя великого голландца именно с легкой руки Пуанкаре) и еще в 1898 году, задолго до Эйнштейна, в работе «Измерение времени» сформулировал принцип относительности, а затем даже ввел четырехмерное пространство-время, теорию которого в сотрудничестве с Эйнштейном позднее разработал Герман Минковский. Примечательно, что сам Эйнштейн очень долго отрицал всякое знакомство с трудами Пуанкаре и не ссылался на него вплоть до начала двадцатых годов (!), однако впоследствии все же признал заслуги французского математика.
Пончики, бублики и прочие сласти
Григорий Перельман и гипотеза Пуанкаре
Григорий Яковлевич Перельман родился и вырос в Ленинграде, учился в знаменитой 239-й школе. В 1982 году выиграл Международную математическую олимпиаду, набрав максимально возможное количество баллов. Степень кандидата наук получил в СПбГУ, затем некоторое время работал в Петербургском отделении математического института РАН; в конце восьмидесятых уехал в США, где работал до середины девяностых, а затем вернулся в Россию; сейчас снова работает в ПОМИ.
Текущее положение дел таково: множество экспертов тщательнейшим образом проверили детали доказательства. Опубликованы много сотен страниц пояснений и комментариев к двум препринтам Перельмана[См., например, http://www.math.lsa.umich.edu/research/ricciflow/perelman.html]. Пока ошибок не найдено, и большинство экспертов склоняются к мысли, что задача действительно решена. Что же касается обязательных публикаций, то представители Clay Mathematics Institute уже выступили с заявлением о том, что могут пересмотреть условия присуждения приза.
Ошибка на ошибке: история вопроса
Однако в его рассуждения вкралась ошибка, которую он сам и нашел, к 1904 году разработав важнейшее понятие фундаментальной группы и построив на его базе контрпример к собственной теореме. Тогда же он наконец-то поставил вопрос правильно.
Алгоритмическая версия
Спустя двадцать лет алгоритм распознавания 3-сферы (за экспоненциальное время) был построен[Abigail Thompson. Thin position and the recognition problem for S3. Math. Res. Lett., 1(5):613–630, 1994.]. Общая же проблема алгоритмического распознавания поверхностей размерности 3 открыта, она активно изучается и сегодня. Для более высоких размерностей давно известна ее неразрешимость, для размерности 2 она была решена еще раньше, а вот в нашем родном трехмерье все почему-то невероятно сложно устроено.
Миллион долларов за дырку от бублика Российский математик решил проблему Пуанкаре, но премию получать не спешит
Ученые считают, что 38-летний российский математик Григорий Перельман предложил верное решение проблемы Пуанкаре. Об этом на научном фестивале в Эксетере (Великобритания) заявил профессор математики Стэнфордского университета Кит Девлин.
Ученые всего мира узнали о достижениях Перельмана из двух препринтов (статей, предваряющих полноценную научную публикацию), размещенных автором в ноябре 2002-го и марте 2003 года на сайте архива предварительных работ Лос-Аламосской научной лаборатории.
Согласно правилам, принятым Научным консультативным советом института Клэя, новая гипотеза должна быть опубликована в специализированном журнале, имеющем «международную репутацию». Кроме того, по правилам Института, решение о выплате приза принимает, в конечном счёте, «математическое сообщество»: доказательство не должно быть опровергнуто в течение двух лет после публикации. Проверкой каждого доказательства занимаются математики в разных странах мира.
Проблема Пуанкаре
Родился 13 июня 1966 года в Ленинграде, в семье служащих. Окончил знаменитую среднюю школу № 239 с углубленным изучением математики. В 1982 году в составе команды советских школьников участвовал в Международной математической олимпиаде, проходившей в Будапеште. Был без экзаменов зачислен на матмех Ленинградского государственного университета. Побеждал на факультетских, городских и всесоюзных студенческих математических олимпиадах. Получал Ленинскую стипендию. Окончив университет, Перельман поступил в аспирантуру при Санкт-Петербургском отделении Математического института им.В.А.Стеклова. Кандидат физико-математических наук. Работает в лаборатории математической физики.
Проблема Пуанкаре утверждает то же самое для трехмерных многообразий (для двухмерных многообразий, таких как сфера, это положение было доказано еще в XIX веке). Как заметил французский математик, одно из важнейших свойств двухмерной сферы состоит в том, что любая замкнутая петля (например, лассо), лежащая на ней, может быть стянута в одну точку, не покидая при этом поверхности. Для тора это справедливо не всегда: петля, проходящая через его отверстие, стянется в точку либо при разломе тора, либо при разрыве самой петли. В 1904 году Пуанкаре высказал предположение, что если петля может стягиваться в точку на замкнутой трехмерной поверхности, то такая поверхность гомеоморфна трехмерной сфере. Доказательство этой гипотезы оказалось чрезвычайно сложной задачей.
Задача, подобная проблеме Пуанкаре, для размерностей 5 и выше была решена в 1960 году Стивеном Смэйлом (Stephen Smale), Джоном Стэллингсом (John Stallings) и Эндрю Уоллесом (Andrew Wallace). Подходы, использованные этими учеными, оказались, однако, неприменимы к четырехмерным многообразиям. Для них проблема Пуанкаре была доказана лишь в 1981 году Майклом Фридманом (Michael Freedman). Трехмерный же случай оказался самым сложным; его решение и предлагает Григорий Перельман.
Необходимо отметить, что у Перельмана есть соперник. В апреле 2002 года профессор математики британского университета Саутгемптон Мартин Данвуди предложил свой метод решения проблемы Пуанкаре и теперь ожидает вердикт от института Клэя.
Специалисты считают, что решение проблемы Пуанкаре позволит сделать серьезный шаг в математическом описании физических процессов в сложных трехмерных объектах и даст новый импульс развитию компьютерной топологии. Метод, который предлагает Григорий Перельман, приведет к открытию нового направления в геометрии и топологии. Петербургский математик вполне может претендовать на премию Филдса (аналог Нобелевской премии, которую по математике не присуждают).
Между тем, некоторые находят поведение Григория Перельмана странным. Вот что пишет британская газета «Гардиан»: «Скорее всего, подход Перельмана к разгадке проблемы Пуанкаре верный. Но не все так просто. Перельман не предоставляет доказательств того, что работа издана в качестве полноценной научной публикации (препринты таковой не считаются). А это необходимо, если человек хочет получить награду от института Клэя. Кроме того, он вообще не проявляет интереса к деньгам».
Список тысячелетия
ЖЮЛЬ АНРИ ПУАНКАРЕ. Фото с сайта www.ibmh.msk.su
1. Проблема Кука (сформулирована в 1971 году)
Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей. Это говорит о том, что решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения.
ДЭВИД ГИЛБЕРТ. Фото с сайта www.krugosvet.ru
Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки. Эта проблема также является одной из нерешенных задач из области логики и информатики. Ее решение могло бы революционным образом изменить основы криптографии, используемой при передаче и хранении данных.
2. Гипотеза Римана (сформулирована в 1859 году)
Некоторые целые числа не могут быть выражены как произведение двух меньших целых чисел, например 2, 3, 5, 7 и так далее. Такие числа называются простыми и играют важную роль в чистой математике и ее приложениях. Распределение простых чисел среди ряда всех натуральных чисел не подчиняется никакой закономерности. Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
3. Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)
4. Гипотеза Ходжа (сформулирована в 1941 году)
В ХХ веке математики открыли мощный метод исследования формы сложных объектов. Основная идея заключается в том, чтобы использовать вместо самого объекта простые «кирпичики», которые склеиваются между собой и образуют его подобие. Гипотеза Ходжа связана с некоторыми предположениями относительно свойств таких «кирпичиков» и объектов.
 |
| ПРОФЕССОР МАРТИН ДАНВУДИ, ТАКЖЕ ПРЕДЛОЖИВШИЙ РЕШЕНИЕ ПРОБЛЕМЫ ПУАНКАРЕ. Фото с сайта www.maths.soton.ac.uk |
6. Проблема Пуанкаре (сформулирована в 1904 году)
Доступно о гипотезе Пуанкаре и доказательстве Перельмана
Лига математиков
382 поста 1.8K подписчиков
Гипотеза Пуанкаре — доказанная математическая гипотеза о том, что всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере.
видел 15 минутный ролик где всё просто и доступно. Тут же и говорить толком не умеют.
внимательно посмотрел, послушал (нет)
А Гамильтон с Перельманом не могли просто понаблюдать за мыльными пузырями, например? Они ведь ведут себя именно так :)))
Ох уж этот неформальный математический стиль
Теорема Пуанкаре простыми словами
Доказательство этой гипотезы российским математиком Григорием Перельманом привело к некоторым очень интересным выводам с точки зрения нашего понимания мира.
Жюль Анри Пуанкаре (1854-1912) возглавлял Парижскую академию наук и был избран в научные академии 30 стран мира. Он имел масштаб Леонардо: его интересы охватывали физику, механику, астрономию, философию. Математики же всего мира до сих пор говорят, что только два человека в истории по-настоящему знали эту науку: немец Давид Гилберт (1862-1943) и Пуанкаре. В 1904 году учёный опубликовал работу, содержавшую среди прочего предположение, получившее название теорема Пуанкаре. Поиск доказательства истинности этого утверждения занял около века.
Математический гений Пуанкаре впечатляет количеством разделов науки, где им были разработаны теоретические основы различных процессов и явлений. Во времена, когда ученые совершали прорывы в новые миры космоса и в глубины атома, было не обойтись без единой основы общей теории мироздания. Такой базой стали ранее неизвестные отрасли математики. Пуанкаре искал новый взгляд на небесную механику, он создал качественную теорию дифференциальных уравнений, теорию автоморфных функций. Исследования ученого стали основой специальной теории относительности Эйнштейна. Теорема Пуанкаре о возвращении говорила среди прочего о том, что понять свойства глобальных объектов или явлений можно исследуя составляющие их частицы и элементы. Это дало мощный толчок научным поискам в физике, химии, астрономии и т.д.
Одна из семи задач тысячелетия
• Равенство классов P и NP (о соответствии алгоритмов решения задачи и методов проверки их правильности).
• Гипотеза Ходжа (о связи объектов и их подобия, составленного для их изучения из «кирпичиков» с определенными свойствами).
• Гипотеза Пуанкаре (всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере).
• Гипотеза Римана (о закономерности размещения простых чисел).
• Теория Янга — Миллса (уравнения из области элементарных частиц, описывающие различные виды взаимодействий).
• Существование и гладкость решений уравнений Навье — Стокса (описывают турбулентность течений воздуха и жидкостей).
• Гипотеза Бёрча — Свиннертон-Дайера (об уравнениях, описывающих эллиптические кривые).
Каждая эта проблема имела очень долгую историю, поиски их решения приводили к возникновению целых новых научных направлений, но единственно правильные ответы на поставленные вопросы не находились. Понимающие люди говорили, что деньги фонда Клэя в безопасности, но так было лишь до 2002 года – появился тот, кто доказал теорему Пуанкаре. Правда, деньги он не взял.
Гипотеза, для которой найдено подтверждение, становится теоремой, имеющей корректное доказательство. Именно это произошло с высказанным Пуанкаре предположением о свойствах трехмерных сфер. В более общем виде этот постулат говорил о гомеоморфности всякого многообразия размерности n и сферы размерности n как необходимом условии их гомотопической эквивалентности. Знаменитая теперь теорема Пуанкаре относится к варианту, когда n=3. Именно в трехмерном пространстве математиков ждали затруднения, для других случаев доказательства были найдены быстрее. Чтобы хоть немного постичь смысл теоремы Пуанкаре, не обойтись без знакомства с основными понятиями топологии.
Топология, говоря о гомеоморфизме, определяет его как взаимно-однозначное соответствие между точками одной и другой фигуры, в некотором смысле неотличимость. Неподготовленному сложно даётся теорема Пуанкаре. Для чайников можно привести самый популярный пример гомеоморфных фигур – шар и куб, также гомеоморфны бублик и кружка, но не кружка и куб. Фигуры гомеоморфны, если одну фигуру можно получить произвольной деформацией из другой, причем это преобразование ограничено некоторыми свойствами поверхности фигуры: её нельзя рвать, прокалывать, разрезать. Если куб раздуть, он легко может стать шаром, если шар примять встречными движениями, можно получить кубик. Наличие дырки у бублика и дырки, образованной ручкой у кружки, делает их гомеоморфными, та же дырка делает невозможным превращение кружки в шар или куб.
Дырка – важное понятие, определяющее свойства объекта, но категория совершенно не математическая. Было введено понятие связности. Его содержат многие топологические постулаты, в том числе и теорема Пуанкаре. Простыми словами можно говорить так: если поверхность шара обернуть петлей из резиновой ленты, она, сжимаясь, соскользнёт. Этого не произойдет, если имеется отверстие, как у тора-бублика, сквозь которое можно продеть эту ленту. Таким образом определяется главный признак сходства или отличия объектов.
Долгий путь к истине
Прошло более полувека, прежде чем появилось решение теоремы Пуанкаре для больших чем 3 размерностей. Стивен Смэйл (род. 1930), Джон Роберт Стэллингс (1935-2008), Эрик Кристофер Зиман (род. 1925) нашли решение для n, равного 5, 6 и равного или больше 7. Только в 1982 году Майкл Фридман (род. 1951) был удостоен высшей математической награды – Филдсовской премии – за доказательство теоремы Пуанкаре для более сложного случая: когда n=4.
Трудное время 90-х заставило молодого ученого уехать на работу в США. Те, кто знал его тогда, отмечали его аскетизм в быту, увлечённость работой, прекрасную подготовку и высокую эрудицию, которые и стали залогом того, что Перельман доказал теорему Пуанкаре. Вплотную он занялся этой проблемой после возвращения в Санкт-Петербург в 1996 году, но начал думать над ней еще в США.
Григорий Яковлевич отмечает, что его всегда увлекали сложные проблемы, такие как теорема Пуанкаре. Доказательство Перельман стал искать в направлении, вынесенном из беседы с профессором Колумбийского университета Ричардом Гамильтоном (род. 1943). Во время пребывания в США он специально ездил из другого города на лекции этого неординарного ученого. Перельман отмечает прекрасное доброжелательное отношение профессора к молодому математику из России. В их разговоре Гамильтон упомянул о потоках Риччи – системе дифференциальных уравнений – как способе решения теорем геометризации.
Впоследствии Перельман пытался связаться с Гамильтоном и обсудить ход работы над задачей, но не получил ответа. Долгое время после возвращения на родину Григорий Яковлевич провел наедине с труднейшей задачей, которой была теорема Пуанкаре. Доказательство Перельмана – итог огромных усилий и самоотречения. Гамильтон пришел в тупик, когда увидел, что при преобразованиях кривых под действием потоков Риччи образуются сингулярные (обращающиеся в бесконечность) зоны, которые не предусматривала теорема Пуанкаре. Простыми словами, Перельману удалось нейтрализовать образование таких зон, и многообразие благополучно превратилось в сферу.
Односвязное 3-мерное многообразие наделяется геометрией, вводятся метрические элементы с расстоянием и углами. Легче понять это на одномерных многообразиях. Гладкая замкнутая кривая на эвклидовой плоскости наделяется в каждой точке касательным вектором единичной длины. При обходе кривой вектор поворачивается с определенной угловой скоростью, которая определяет кривизну. Где линия изогнута сильнее, кривизна больше. Кривизна положительна, если вектор скорости повернут в сторону внутренней части плоскости, которую делит наша линия, и отрицательна, если повернут вовне. В местах перегиба кривизна равна 0.
Он взошел на свой Эверест, каким признается математиками теорема Пуанкаре. Доказательство Перельман выложил в Интернет в виде трех небольших статей. Они немедленно вызвали ажиотаж, хотя русский математик не пошел положенной дорогой – публикация в специализированном журнале в сопровождении профессиональных рецензий. Григорий Яковлевич в течение месяца разъяснял в университетах США суть своего открытия, но число до конца понявших ход его мысли увеличивалось очень медленно. Лишь через четыре года появилось заключение самых больших авторитетов: доказательства русского математика корректны, первая из проблем тысячелетия решена.
Ему пришлось пережить ажиотаж и хамство в соцсетях, молчание тех, кого он уважал, и крики других, учивших его жизни. Энергичные китайцы сначала оценили его вклад в решение проблемы в 25 %, себе и другим насчитав 80! Потом вроде бы пришло мировое признание, но выдержать такое дано не каждому.
Григорий Перельман: многомерная фигура
Про одного из самых выдающихся математиков современности. Григорий Перельман.
В основе курса СССР на точные науки, подготовившего почву для достижений ядерной физики, космонавтики и спортивных шахмат, лежала сильная математическая традиция. Оформившись в 1930-х, она подарила миру таких ученых, как Андрей Колмогоров, Александр Гельфонд, Павел Александров и многих других, которые преуспели в традиционных (алгебра, теория чисел) и новых направлениях математики (топология, теория вероятностей, математическая статистика). По масштабам интересов и интеллектуальных ресурсов сравниться с советской могли разве что американская и китайская школы. Но сравнением они не ограничивались: на макроуровне царица наук развивалась в противоречивой обстановке дружелюбной подозрительности. Важную роль такие взаимовлияния сыграли и в профессиональной жизни Григория Перельмана – признанного математического гения, окончательно доказавшего гипотезу Пуанкаре и решившего таким образом одну из семи «задач тысячелетия».
Сurriculum vitæ. Первые страницы
Григорий Яковлевич Перельман родился 13 июня 1966 года в Ленинграде в семье инженера-электрика и учительницы математики, а спустя десять лет у него появилась сестра – в будущем тоже кандидат (точнее, PhD) математических наук. Помимо любви к классической музыке, привитой матерью, Григорий с детства проявлял интерес к точным наукам: в пятом классе он начал посещать математический центр при Дворце пионеров, а после восьмого перешел в школу № 239 с углубленным изучением математики, которую окончил без золотой медали только из-за недостатка баллов по нормативам ГТО. В 1982 году он в составе школьной команды получил золотую медаль на 23-й Международной математической олимпиаде в Будапеште и вскоре был зачислен на математико-механический факультет Ленинградского государственного университета без сдачи экзаменов.
В вузе за примерную учебу Перельман получал Ленинскую стипендию. Окончив университет с отличием, он поступил в аспирантуру на базе Ленинградского отделения Математического института имени В. А. Стеклова РАН. В 1990 году под научным руководством академика Александра Даниловича Александрова (основоположника так называемой геометрии Александрова – раздела метрической геометрии) Перельман защитил кандидатскую диссертацию на тему «Седловые поверхности в евклидовых пространствах». Затем в должности старшего научного сотрудника продолжил работать в лаборатории математической физики института Стеклова, успешно развивая теорию пространств Александрова.
В начале 1990-х Перельману довелось поработать в нескольких уважаемых исследовательских учреждениях США: в Университете штата Нью-Йорк в Стоуни-Брук, Курантовском институте математических наук и Калифорнийском университете в Беркли.
Поворотной для молодого математика стала встреча с Ричардом Гамильтоном, область научных интересов которого простиралась в плоскости дифференциальной геометрии – нового направления, широко используемого в общей теории относительности. В своих работах по топологии многообразий американский ученый впервые использовал систему дифференциальных уравнений под названием поток Риччи – нелинейный аналог уравнения теплопроводности, который описывает не распределение температуры, а деформацию хаусдорфова пространства, локально эквивалентного евклидовому.
Благодаря этой системе уравнений Гамильтону удалось наметить решение одной из семи «задач тысячелетия» – по сути, разработать подход к доказательству гипотезы Пуанкаре.
Благосклонность зарубежного коллеги и столь фундаментальная проблема произвели на Перельмана большое впечатление. В то время он продолжал сглаживать углы пространств Александрова – технические трудности казались непреодолимыми, и ученый вновь и вновь возвращался к идее потока Риччи. По словам советского математика Михаила Громова, сосредоточившись на этих задачах, Перельман стал еще более аскетичным, что вызывало тревогу у его близких.
В 1994 году он получил приглашение прочесть лекцию на Международном конгрессе математиков в Цюрихе, а сразу несколько научных организаций, в том числе Принстонский и Тель-Авивский университеты, предложили ему место в штате. В ответ на просьбу Стэнфордского университета предоставить резюме и рекомендации ученый заметил: «Если они знают мои работы, им не нужно мое CV. Если же они нуждаются в моем CV, они не знают мои работы». Несмотря на такое обилие заманчивых предложений, в 1995 году он принял решение вернуться в «родной» институт Стеклова.
В 1996-м Европейское математическое общество присудило Перельману его первую международную премию, которую по каким-то причинам он отказался получать.
Помимо непритязательности в быту, пристрастия к музыке (Перельман играет на скрипке) и строгой приверженности научной этике, ученого уже тогда отличал интерес к параллельному решению сложных задач. В 1994 году он доказал гипотезу о душе. В дифференциальной геометрии под «душой» (S) подразумевают компактное тотально выпуклое тотально геодезическое подмногообразие риманова многообразия (M, g). В простейшем случае, то есть в случае евклидова пространства Rn (n отражает мерность), душой будет любая точка этого пространства.
Перельман доказал, что душа полного связного риманова многообразия с секционной кривизной K ≥ 0, секционная кривизна одной из точек в котором строго положительна во всех направлениях, является точкой, а само многообразие диффеоморфно Rn. Математиков потрясло редкостное изящество доказательства Перельмана: выкладки заняли всего две страницы, в то время как «доперельмановские» попытки решения излагались в длинных статьях и оставались незавершенными.
Доказательство гипотезы Пуанкаре, или Благодатное слияние кухни с операционной
На рубеже 19–20 веков гениальный французский математик Анри Пуанкаре увлеченно закладывал фундамент топологии – науки о свойствах пространств, которые остаются неизменными при непрерывных деформациях. В 1900 году ученый предположил, что трехмерное многообразие, все группы гомологий которого как у сферы, гомеоморфно сфере (топологически ей эквивалентно). В общем же случае, для многообразий любой мерности, гипотеза звучит примерно так: всякое односвязное замкнутое n-мерное многообразие гомеоморфно n-мерной сфере. Здесь необходимо хоть немного расшифровать термины, которыми так свободно оперировал Пуанкаре.
Электронная модель преобразования Пуанкаре – Перельмана / ©Wikipedia
Двумерное многообразие – это плоскость: например, поверхность сферы или тора («бублика»). Трехмерное многообразие представить сложнее: в качестве одной из его моделей рассматривают додекаэдр, противоположные грани которого особым образом «склеены» друг с другом – отождествлены. Именно для случая трехмерного многообразия гипотеза Пуанкаре оставалась крепким орешком на протяжении целого века. Что касается гомеоморфизма, то любые замкнутые, без дыр, поверхности гомеоморфны, то есть могут непрерывно и однозначно преобразовываться (отображаться) друг в друга и деформироваться в сферу, а вот с тором, например, такое без разрыва поверхности не пройдет, поэтому он негомеоморфен сфере, зато гомеоморфен… кружке – той самой, из кухонного шкафчика. Гомология – понятие, позволяющее строить специфические алгебраические объекты (группы, кольца) для изучения топологических пространств – считается, что общеалгебраические структуры устроены проще, чем топологические. Вот простейшие примеры гомологии: замкнутая линия на поверхности гомологична нулю, если она служит границей какого-то участка этой поверхности; гомологичной нулю является любая замкнутая линия на сфере, у тора же такая линия может и не быть гомологичной нулю.
Группы – разнообразные множества, удовлетворяющие особым условиям, – оказались крайне полезными для описания топологических инвариантов – характеристик пространства, не меняющихся при его деформациях. Очень востребованы, в частности, группы гомологий и фундаментальные группы. Группа гомологии ставится в соответствие топологическому пространству для алгебраического исследования его свойств. Фундаментальная группа – это множество закрепленных (начинающихся и заканчивающихся) в отмеченной точке отображений отрезка в пространство (петель), измеряющих количество «дырок» в этом пространстве («дырки» возникают из-за невозможности непрерывно деформировать отрезок в точку). Такая группа представляет собой один из топологических инвариантов: гомеоморфные пространства имеют одну и ту же фундаментальную группу.
Проективный образ квазизамкнутого мира квантового вакуума с многосвязной топологией Пуанкаре – Перельмана
В первоначальном варианте гипотеза Пуанкаре для трехмерных многообразий оставалась «разрешимой»: она позволяла ослабить условие на фундаментальную группу до условия на группу гомологий. Однако вскоре Пуанкаре исключил это допущение, продемонстрировав пример нестандартной трехмерной гомологической сферы с конечной фундаментальной группой – «сферу Пуанкаре». Такой объект мог быть получен, например, склеиванием каждой грани додекаэдра с противоположной, повернутой на угол π/5 по часовой стрелке. Уникальность сферы Пуанкаре заключается в том, что она гомологична трехмерной сфере, но при этом отличаться от нее в евклидовом пространстве.
В окончательной формулировке гипотеза Пуанкаре звучала следующим образом: всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере. Доказательство этой гипотезы сулило новые возможности для моделирования многомерных пространств. В частности, полученные с помощью космического зонда WMAP данные позволяли рассматривать додекаэдрическое пространство Пуанкаре как возможную математическую модель формы Вселенной.
И вот, в 2002–2003 годах (к тому моменту тематическая переписка Перельмана с Гамильтоном уже сошла на нет) пользователь с ником Grisha Perelman с интервалом в несколько месяцев разместил на сервере препринтов arXiv.org три статьи (1, 2, 3), содержащие решение задачи, еще более общей, чем гипотеза Пуанкаре, – гипотезы геометризации Терстона. И первая же публикация стала международной научной сенсацией, хотя из-за антипатии автора к бюрократии ни одна из статей так и не попала на страницы рецензируемых журналов. Выкладки Перельмана были настолько лаконичны и в то же время сложны, что во всеобщий восторг просто не могло не вкрасться недоверие, поэтому с 2004 по 2006 годы проверку работ Перельмана проводили сразу три группы ученых из США и Китая.
Чтобы деформировать риманову метрику на односвязном трехмерном многообразии до гладкой метрики целевого многообразия, Перельман ввел новый метод изучения потока Риччи, который вполне справедливо назвали теорией Гамильтона – Перельмана. Изюминка метода заключалась в том, чтобы при подходе к сингулярности, возникающей при деформации метрики, остановить применяемый к многообразию поток и вырезать «шею» (открытую область, диффеоморфную прямому произведению) или выбросить малую связную компоненту, «заклеив» две полученные «дырки» шарами. По мере повторения этой хирургической операции выбрасывается все, при этом каждый кусок диффеоморфен сферической пространственной форме, а итоговое многообразие является сферой.
В итоге Перельману удалось не только доказать гипотезу Пуанкаре, но и полностью классифицировать компактные трехмерные многообразия. Вероятно, этого никогда бы не случилось, если бы в длинном списке отличительных черт Перельмана не значилась непоколебимая настойчивость. Бывший учитель математики, кандидат физико-математических наук Сергей Рушкин вспоминал: «Гриша начал очень много работать в девятом классе, и у него оказалось очень ценное для занятий математикой качество: способность к очень длительной концентрации внимания без особых успехов внутри задачи.
Все-таки человеку нужна психологическая подпитка, нужны психологические успехи, чтобы заниматься чем-то дальше. Фактически гипотеза Пуанкаре – это почти девять лет без знания того, решится задача или не решится. Понимаете, там даже невозможны были частичные результаты. Не доказалась теорема в полном объеме – иной раз можно опубликовать даже двадцатистраничную статью по тому, что все-таки получилось. А там – или пан, или пропал». Вечность в кармане
В 2003 году Григорий Перельман принял приглашение прочесть о своих работах серию публичных лекций и докладов в США. Но его не понимали ни студенты, ни коллеги. В течение нескольких месяцев математик терпеливо объяснял, в том числе и в личных беседах, свои методы и идеи. Во время «американского турне» Перельман рассчитывал и на плодотворный разговор с Гамильтоном, но он так и не состоялся. Вернувшись в Россию, ученый продолжил отвечать на сыпавшиеся от математиков вопросы по электронной почте. В 2005 году, устав от атмосферы публичности, интриг и бесконечных объяснений, связанных с затянувшейся проверкой его выкладок, Перельман уволился из института и фактически оборвал профессиональные связи.
В 2006 году все три группы экспертов признали доказательство гипотезы Пуанкаре состоявшимся, на что китайские математики во главе с Яу Шинтуном, чья фамилия красуется в названии целого класса многообразий (пространств Калаби–Яу), ответили попыткой оспорить приоритет Перельмана. Правда, выбранный для этого инструментарий оказался неудачным: он сильно походил на плагиат. Оригинальная статья учеников Яу, Цао Хуайдуна и Чжу Сипина, занявшая весь июньский номер The Asian Journal of Mathematics, аннотировалась как окончательное доказательство гипотезы Пуанкаре с применением теории Гамильтона – Перельмана. Если верить журналистским расследованиям, то еще перед публикацией этой статьи, открыто курируемой Яу, последний потребовал у 31 математика из редколлегии журнала в кратчайшие сроки прокомментировать ее, однако саму статью тогда почему-то не предоставил.
Яу Шинтун не просто отлично знал Гамильтона, но и сотрудничал с ним, и заявление Перельмана об успешном решении задачи стало для обоих ученых сюрпризом: после долгих лет работы над ней они рассчитывали, несмотря на временную заминку, прийти к финишу первыми. Впоследствии Яу подчеркивал, что препринты Перельмана выглядели неряшливо и невнятно из-за отсутствия подробных расчетов (автор приводил их по мере необходимости в ответ на запросы независимых экспертов), и это мешало ему и всем остальным понять доказательство в полной мере.
Мир суперновой физики пространства-времени в теореме Пуанкаре – Перельмана
Попытка умалить заслуги Перельмана – а Яу даже любезно подсчитал их в процентном выражении – не удалась, и вскоре китайские ученые подкорректировали заглавие и аннотацию своей статьи. Теперь ее нужно было воспринимать не как свидетельство «венценосного достижения» китайских математиков, а как «самостоятельную и подробную экспозицию» доказательства гипотезы Пуанкаре, произведенного Гамильтоном и Перельманом – без посягательств на чей-то приоритет. Перельман прокомментировал действия Яу так: «Я не могу сказать, что я возмущен, остальные поступают еще хуже…» И правда, китайского математического гения можно понять: ревностную поддержку статьи своих учеников Яу позже объяснял желанием представить окончательное доказательство в удобоваримом, каждому понятном виде и закрепить в истории заслуги соотечественников в решении этой задачи тысячелетия – а ведь их и на самом деле отрицать нельзя…
Тем временем, в августе 2006 года, Перельману присудили Филдсовскую премию «за вклад в геометрию и его революционные идеи в изучении геометрической и аналитической структуры потока Риччи». Но, как и десять лет назад, от награды Перельман отказался, а заодно и сообщил о нежелании далее пребывать в статусе профессионального ученого. В декабре того же года журнал Science впервые признал математическую работу – работу Перельмана – «Прорывом года». Тогда же СМИ разразились серией статей, освещающих это достижение, правда, с упором на сопровождавший его конфликт. Для защиты своей позиции Яу обратился к адвокатам и пригрозил судом «опорочившим его имя» журналистам, однако угрозу так и не осуществил.
В 2007 году Перельман занял девятое место в рейтинге «Сто ныне живущих гениев», опубликованном в The Daily Telegraph. А спустя три года Математический институт Клэя присудил за решение задачи тысячелетия «Премию тысячелетия» – впервые в истории. Поначалу премию в один миллион долларов Перельман проигнорировал, а затем официально отверг: «Если говорить совсем коротко, то главная причина – это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой».
Инфляционная экспансия в представлении многообразия Пуанкаре – Перельмана
В 2011 году «Премию тысячелетия», от которой отказался Перельман, Институт Клэя решил направить на оплату труда молодых, подающих надежды математиков, для которых в парижском Институте Анри Пуанкаре учредили специальную временную должность. Тогда же Ричарду Гамильтону присудили Премию Шао по математике за создание программы решения гипотезы Пуанкаре. Премиальный миллион долларов в тот год пришлось разделить поровну между Гамильтоном и вторым математическим лауреатом, Деметриосом Христодулу.
Доброе отношение к Гамильтону Перельман сохранил, несмотря на несостоявшийся диалог и очевидную неудовлетворенность старшего коллеги финалом этой научной истории. А это многое говорит о человеке. По слухам, Григорий Яковлевич продолжает жить в Санкт-Петербурге, периодически посещая Швецию, где сотрудничает с местной компанией, занимающейся научными разработками. Ну а шесть задач тысячелетия все еще ждут своего гения.