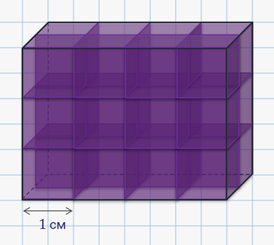
что означает измерить объем фигуры

ВОПРОСЫ

1. Какими свойствами обладает объем фигуры?

1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.

2. Какой куб называют единичным?

3. Приведите примеры единиц измерения объема.

4. Что означает измерить объем фигуры?

5. Чему равен объем прямоугольного параллелепипеда с измерениями а, b, c?

6. По какой формуле вычисляется объем куба?

7. Как вычислить объем прямоугольного параллелепипеда, зная его площадь основания и высоту?

РЕШАЕМ УСТНО

1. Заполните пропуски в цепочки вычислений:

2. Сколько необходимо использовать кубиков с ребром 1 см, сложить кубик с ребром 2 см?

Нужно взять 8 кубиков с ребром 1 см.

3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?

УПРАЖНЕНИЯ

617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?

618. Фигуры, изображенные на рисунке 179, сложены из кубиков, ребра которых равны 1 см. Найдите объем каждой фигуры.

619. Вычислите объем прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.

620. Чему равен объем куба, ребро которого равно 6 см?

621. Чему равен объем прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?

622. Выразите:
1) в кубических миллиметрах: 7 см3, 38 см3; 12 см3 243 мм3; 42 см3 68 мм3; 54 см3 4 мм3; 1 дм3 20 мм3; 18 дм3 172 см3; 35 дм3 67 см3 96 мм3;
2) в кубических дециметрах: 4 м3; 264 м3; 10 м3 857 дм3; 28 м3 2 дм3; 44 000 см3; 5 430 000 см3.

623. Выразите в кубических сантиметрах: 8 дм3; 62 дм3; 378 000 мм3; 520 000 мм3; 78 дм3 325 см3; 56 дм3 14 см3; 8 м3 4 дм3 6 см3.

625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объем данного параллелепипеда.

629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объем равен 960 м3, а площадь пола равна 192 м2. Найдите высоту спортивного зала.

630. Найдите объем фигуры, изображенной на рисунке 180 (размеры даны в сантиметрах).

631. Найдите объем фигуры, изображенной на рисунке 181 (размеры даны в сантиметрах).

632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если 1 см3 цинка составляет 7 г.

633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм3 земли?

634. Куб и прямоугольный параллелепипед имеют равные объемы. Найдите площади поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.

635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объем первого куба больше объема второго?

638. В бассейн, площадь которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?

639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объем оставшейся части.

640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ

642. Из двух населенных пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?

643. Найдите значение выражения:

ЗАДАЧА ОТ МУДРОЙ СОВЫ

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Перечень вопросов, рассматриваемых на уроке:

Объём прямоугольного параллелепипеда.

Формула объёма прямоугольного параллелепипеда.

Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.

Основные свойства объёма:

— равные тела имеют равные объёмы;

— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.

Теоретический материал для самостоятельного изучения

С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.

Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.

Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см 3 ). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ) и тому подобное.

Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.

Объём обозначается заглавной латинской буквой V.

Рассмотрим свойства объёмов.

Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.

Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Следствие из основных свойств объёмов.

Объём куба с ребром 1/n равен 1/n 3

Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см 3 ). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём прямоугольного параллелепипеда

Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.

По доказанному в первом случае, левая часть неравенства представляет собой объём V_n прямоугольного параллелепипеда P_n с измерениями a_n, b_n, c_n, а правая часть – это объём V_n’ прямоугольного параллелепипеда P_n’ с измерениями a_n’, b_n’, c_n’. Так как параллелепипед P содержит в себе параллелепипед P_n, а сам содержится в параллелепипеде P_n’, то объём V параллелепипеда P заключён между V_n, = a_nb_nc_n и V_n’= a_n’b_n’c_n’. Будем неограниченно увеличивать n. Тогда 1/10 n будет становиться сколь угодно малым, и поэтому произведение a_n’b_n’c_n’ будет сколь угодно мало отличаться от числа, выраженного произведением a_nb_nc_n. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением a_nb_nc_n, а значит, они равны.V = abc, что и требовалось доказать.

Примеры и разбор решения заданий тренировочного модуля.

№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.

Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:

V = 15 ∙ 20 ∙ 25 = 7500 см 3

№2.

AD = 960 : 8 : 20 = 6 см

Найдём АС, воспользовавшись теоремой Пифагора:

Источник

Измерение площади и объёма

Урок 11. Наглядная геометрия 5–6 классы ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Измерение площади и объёма»

Понятие площади нам хорошо известно из повседневной жизни. Каждый понимает смысл понятий площадь комнаты, площадь садового участка, площадь озера.

При этом на практике людям часто приходится выяснять, например, какое из двух полей больше, для того чтобы узнать, для засева какого из них требуется больше зерна. При решении этого вопроса мы не учитываем, какую форму имеют поля. Нас интересует, какое из них занимает больше места, то есть имеет большую площадь.

С геометрической точки зрения поле представляет собой фигуру, которая занимает некоторую часть плоскости. Именно для плоских фигур мы выясняем, какая из них занимает больше места на плоскости. Величину той части плоскости, которую занимает плоская фигура, называют площадью фигуры.

Теперь давайте вспомним, что означает измерить отрезок.

Итак, измерить отрезок означает подсчитать, сколько единичных отрезков в нём укладывается.

Для измерения площади фигуры поступают таким же образом. То есть выбирают единицу измерения площади и находят число, которое показывает, сколько раз выбранная единица содержится в измеряемой фигуре.

Обратите внимание и на другие единицы измерения площади.

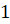
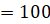
А вот для измерения больших площадей ввели несколько единиц измерения. 1 гектар – это квадрат, сторона которого равна 100 м. 1 ар – это квадрат, сторона которого равна 10 м. га а.

Вы, наверное, слышали, как говорят «участок величиной 5 соток», «поле площадью 30 гектаров».

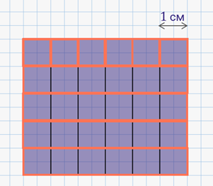
Измерить площадь фигуры означает подсчитать, сколько единичных квадратов в ней укладывается.

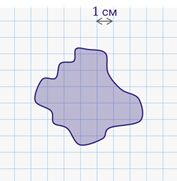
Несложно найти площадь фигуры, которая состоит из квадратных метров, квадратных сантиметров и так далее. А как быть с площадью произвольной фигуры?

Давайте возьмём лист клетчатой бумаги и нарисуем на нём какую-нибудь фигуру.

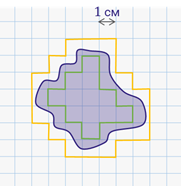
Видим, что ровно 12 целых клеток содержится внутри нашей фигуры. А самое меньшее число клеток, которые покрывают фигуру, равно 36.

Величина 12 см 2 есть площадь фигуры, измеренная с недостатком. Величина 36 см 2 есть площадь фигуры с избытком.

В данной ситуации в качестве значения площади возьмём полусумму измерений с недостатком и избытком. Итак, 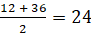. То есть 24 см 2 – приближённое значение площади.

Если продолжить этот процесс, то можно найти площадь данной фигуры ещё точнее.

Со словом «объём» мы часто встречаемся в обыденной жизни. Например, мы можем говорить: «объём жидкости в сосуде», «объём информации», «объём выполненных работ».

С геометрической точки зрения объёмом называют величину той части пространства, которую занимает пространственная фигура.

Все остальные единицы измерения объёма получаются из единиц измерения длины таким же образом.

Часто 1 дм 3 называют литром. В повседневной жизни мы чаще всего измеряем объём жидкости в литрах.

Переход от одних единиц измерения к другим осуществляется так же, как и при измерении площади.

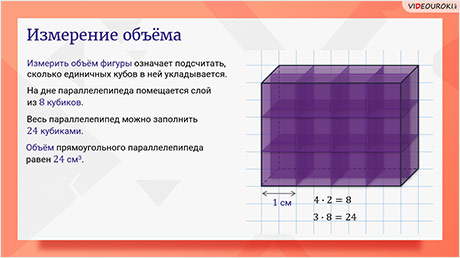
Измерить объём фигуры означает подсчитать, сколько единичных кубов в ней укладывается. Например, найдём объём прямоугольного параллелепипеда. Начнём укладывать кубики с ребром 1 см на дно прямоугольного параллелепипеда. Итак, сначала положим ряд кубиков вдоль длинной стены. У нас поместилось 4 таких кубика. Затем вдоль этого ряда уложим ещё 1 ряд из 4 кубиков.

Получается, что на дне параллелепипеда помещается слой из 8 кубиков.

При решении задач на измерение объёма совсем не обязательно разбивать пространство на кубические единицы, а затем мельчить на меньшие кубики (как мы это делали при нахождении площади произвольной фигуры).

Мы можем поступить следующим образом. Сосуд в виде единичного куба заполним какой-нибудь жидкостью, например, водой. Тогда получившееся количество воды будет соответствовать объёму одной кубической единицы.

Разливая это количество воды в разные по форме сосуды, мы будем получать единичные объёмы различной формы. Именно так мы часто поступаем во многих практических ситуациях. В хозяйстве с помощью бутылок разных объёмов мы можем измерить объёмы различных сосудов с достаточной нам точностью.

В геометрии, кроме измерения длин, площадей и объёмов, надо уметь измерять углы. И мы на одном из предыдущих занятий научились это делать с помощью транспортира. Вы знаете, что единица измерения угла – градус.

Давайте возьмём круг и разделим его на 360 частей. Угол, образованный двумя соседними лучами, равен .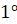

Но есть и более мелкие единицы измерения угла. Минута – одна шестидесятая часть градуса. Минуты обозначают одним штрихом сверху ().

Есть и ещё более мелкая единица измерения угла. Секунда – одна шестидесятая часть минуты. Секунды обозначают двумя верхними штрихами ().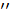

Например, запись 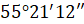читается так: 55 градусов 21 минута 12 секунд.

Дольные единицы углов называют так же, как и единицы времени.

В повседневной жизни человеку постоянно приходится измерять множество различных величин: время, скорость, расстояние, массу, громкость звука и так далее.

При этом иногда нам удобнее с помощью некоторой единицы измерить не соответствующую ей величину. Так, например, говоря о расстоянии между школой и домом, мы чаще всего называем время, за которое доходим из школы домой (или наоборот).

Отметим, что часто при измерении каких-либо величин человеку приходится проявлять изобретательность. Например, нельзя взять и измерить радиус земного шара.

Источник