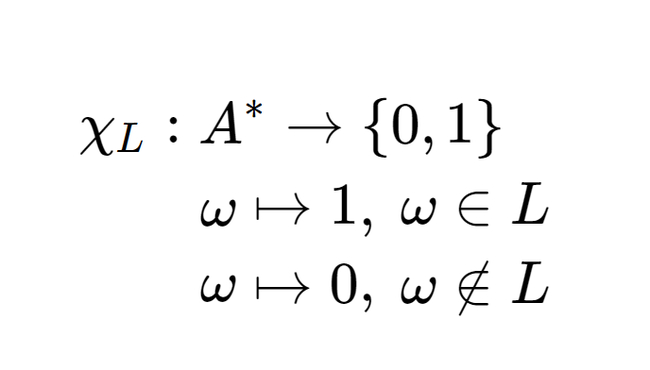что означает математический склад ума
Все об аналитическом складе ума: ТОП-7 упражнений для развития
Если человек совершает свои поступки, руководствуясь логикой и разумными выводами, после глубокого осмысления, анализа событий, можно сказать, что у него аналитический склад ума. Не всякий индивидуум поступает в соответствии с разумными доводами. Некоторые делают то, что им хочется, следуя всплескам своих эмоций и переживаний.
Аналитический склад ума: что это значит
Аналитические способности называют еще математическими и техническими. Они свидетельствуют о том, что субъект умеет продумывать и мыслить логично, выстраивая разумную последовательную цепочку. Люди, умеющие собирать факторы, анализировать их, выстраивать в определенную закономерность отличаются аналитическим способом мышления. Это приводит их к успешным и адекватным итогам.
Фактически почти все способны думать логично. Но не каждый умеет выстраивать правильные цепочки, анализировать и приходить к нужным результатам.
Как определить технический склад ума
Математический склад ума практики психологи определяют необычным способом. Испытатель предлагает сжать обе руки в замок и оставить в такой позиции.
Исследователи считают, что правое полушарие мозга работает в области:
Левое полушарие работает в другом режиме:
У каждого человека работают оба полушария. Но все же одно всегда несколько преобладает. Согласно теории, если большой палец правой руки оказывается в замке сплетенных рук сверху, это значит у вас больше работает левое полушарие. То есть логика у вас сильнее интуиции, склад ума технический.
Если бы у испытуемого человека большой палец левой руки оказался сверху сплетенного замка, это означало бы что работает больше правое полушарие, отвечающее за образность и творческое начало.
Еще один легкий способ определить, какое полушарие у вас лучше работает. Для этого надо представить, что вы прицеливаетесь, чтобы выстрелить из воображаемого пистолета. Обратите внимание, какой глаз прищурен? Если открытым остался правый глаз, он ведущий, значит у вас лучше работает левое аналитическое полушарие. Если открытым остался левый глаз, рабочее правое творческое полушарие.
Но не стоит думать, что все люди делятся строго по работе полушарий. У многих одинаково развиты способности в математике и литературе. Особенно это заметно в России. Жители других стран, которые слишком зацикливаются на узкой специализации человека, постоянно удивляются тому, что россияне все умеют.
Такое разностороннее развитие людей очевидно связано с суровым климатом, в котором они живут. Для простого выживания человеку в жестких условиях надо много уметь и знать.
Как развить математический склад ума
Развивать логическое мышление у детей легко. Для этого достаточно старательно выполнять все домашние задания, в которых много математических задачек. Алгебра, физика, химия показывают примеры построения логических цепочек и уравнений.
Если ребенок любит гимнастику для ума, можно с ним играть в шахматы. Более легкий вариант – шашки и уголки. Складывать пазлы в живописные картинки сегодня любят даже взрослые и студенты.
Отгадывать ребусы и головоломки, заполнять квадратики в кроссвордах и сканвордах очень полезно для развития разума.
Развивается математический образ мышления, когда человек учится танцевать или занимается спортивной, художественной гимнастикой. Для выполнения сложных упражнений с множеством трудных, технически продуманных элементов, пригодится аналитический склад ума. При этом, для красивого выполнения бального, классического, спортивного танца нужно и творческое начало. Поэтому люди сложных технических видов спорта образованные, разносторонние, интеллигентные личности.
Человек с математическим складом ума производит посадки домашнего огорода так, чтобы на маленькой площади могло вырасти много разных растений. Например, между рядами кукурузы удобно посадить вьющуюся фасоль. Ее ветки будут опираться на стебли кукурузы, не потребуется втыкать в землю дополнительные столбики. Фасоль удобно посадить и возле забора. Научная организация трудовой деятельности, смекалка и сообразительность помогают любому специалисту.
Идеальные профессии
Любой индивидуум с первых дней жизни бывает наделен уникальными формами тела, мозга, конечностей, органов осязания. Эти, данные от рождения качества, развиваясь, образуют у людей разные психические и физические склонности.
Склонности делятся на общие и специализированные. Очень важно выбирать специальность, подходящую к индивидуальным качествам человека.
Физические способности нужны в тех профессиях, где нужна выносливость, сила, ловкость:
Нельзя сказать, что эти специальности не требуют мышления. Массажисту надо помнить множество разных приемов и способов массажа для разных частей тела. Пожарный должен знать устройство всех механизмов и строений, в которых приходится тушить пожар. Полицейским надо понимать логику преступников, чтобы их быстрее задерживать.
Развитый ум и интеллект, хорошая эрудиция, разностороннее образование нужны в следующих специальностях:
Степень умственного развития определяется не только генетическими особенностями. Жизненный опыт, полученные знания, эрудиция, сильно влияют на развитие ума. Склад ума – это уникальный метод обработки получаемой информации. Он развивается на протяжении жизни.
Изучив собственный склад ума легко предположить успех в выбранной профессии.
К примеру, коммуникативные способности важны в специальностях, связанных с обслуживанием, учебой, воспитательным процессом, решением организационных вопросов.
Специальности, требующие умения адекватно разговаривать, сохранять спокойствие в любых ситуациях:
Чтобы во время учебы выбрать будущую профессию для себя, надо стараться одинаково учить любые уроки. Тогда вы почувствуете, какие предметы даются легче, какие труднее. Конечно, есть ученики, талантливые по всем предметам, но основная масса успешнее осваивает лишь часть.
Тем, кто лучше усваивает историю, обществоведение можно посоветовать стать юристом. Им легко будет запомнить все нюансы уголовного дела.
Если вам легко даются ботаника, биология, химия, анатомия, из вас может получиться хороший врач.
Тем, кто легко решает алгебраические уравнения, задачки по физике, лучше стать инженером. Математический склад ума пригодится для решения технических вопросов. Хороший программист, конструктор, настройщик и ремонтник приборов очень нужны в век расцвета цифровых технологий.
Аналитический склад ума
Фразы «математический склад ума» и «гуманитарный склад ума» — не глупый набор слов. Эти понятия имеют под собой определенные основания. Ученые заметили, что полушария человеческого мозга развиваются по-разному. Левое несет ответственность за анализирование, техническое мышление, логику. А правое – за эмоциональность, образность мышления, творчество.
Действительно несчастными являются те личности, у которых одно полушарие целиком превалирует над вторым. Если аналитический склад ума доведен до максимума, то такой человек оказывается асоциальным, нечувствительным, полностью погруженным в науку. Но и личности с доминированием образного мышления нелегко: человек постоянно строит воздушные замки, фантазирует, он легко поддается влиянию. Но у большей части людей оба полушария развиты почти одинаково, с маленьким «перевесом» в одну из сторон.
Что значит аналитический склад ума?
Чтобы объяснить, что значит понятие «аналитический склад ума», требуется вспомнить о разных назначениях полушарий мозга. Если у индивида преобладает работа левой половины мозга, то у него аналитический ум, здесь разум превалирует над эмоциями.
Трудом, который требует анализа, способен заниматься каждый, кто умеет сопоставить данные, сделать вывод. Подобный склад мышления – это работа с программами на ПК, документами, а не с людьми. Сегодня немало тренинговых центров создают программы, помогающие развивать мышление аналитика.
К другим особенностям аналитиков стоит отнести то, что они сначала размышляют, а потом приступают к действию. Но им трудно разобраться в ситуации, если требуется воображение. К тому же, люди с умением анализировать только с виду кажутся бесчеловечными и холодными. Это только внешняя оболочка, для них главную роль играют факты. Нередко логика и аналитика переплетается с творческим восприятием мира, креативностью. В этом случае у человека возникает талант к чему-либо. Это редкое сочетание.
Аналитический склад ума. Плюсы и минусы
Аналитический склад ума имеет собственные плюсы и минусы. Нельзя говорить, что какой-то определенный вид мышления лучше. Во всем есть преимущества и недостатки. Необходимо правильно их оценивать, чтобы превращать минус в положительное качество. Люди не могут сами выбирать тип мысли, но способны скорректировать его.
Тем, кто обладает доминирующим аналитическим мышлением, требуется новая информация, анализирование данных постоянно. Человек разбирается в проблеме долго, а на итоговое решение времени почти нет. В ситуации, когда нужно быстрое реагирование, аналитики впадают в ступор. Подобные люди не любят перемены, живут по установленным распорядкам.
Как развивать аналитический склад ума
Если у вас преобладает образное мышление, то вам интересно узнать, как развивать аналитический склад ума. Существуют разнообразные упражнения. Начинать их стоит с мелких нагрузок: сканвордов, ребусов, задач на логику. Действенные тренинги – игры в слова. Неплохо способствует развитию аналитического мышления чтение качественных детективов. Ведь по мере прочтения человек размышляет над основным вопросом книги, ищет злодеев.
Отличное развитие умения анализировать – шашки и шахматы. Кроме того, созданы специфические программы, помогающие развивать навык анализа фактов. Всевозможные программы по географии, истории дарят много новой информации. Думая над различными ситуациями и событиями, человек проводит анализ информации, предполагает варианты развития, схемы.
Кроме того, в ходе работы над собой стоит помнить, что аналитика и логика неразделимы. Потому, если вы часто решаете логические задачки, то учитесь перестраивать мышление. Мы получаем базовые аналитические навыки в школе на уроках математики. Но с течением времени часто люди уделяют меньше внимания развитию, считая, что в работе это не требуется.
У людей аналитическое мышление формируется по-своему, с различным результатом и скоростью. В особенности стремительно умение анализировать совершенствуется при изучении программирования, работе с техническими приборами и механизмами, огромным количеством данных.
Итак, некоторые шаги для развития умения мыслить логично. Придумывайте ситуации. Эта техника отличается доступностью и простотой, потому что вам нужно немного времени и ваш мозг. Суть лежит в придумывании ситуаций, установке целей и формировке действенных выходов и решений. К примеру, вы решили полететь в космос. Для этого вам необходимо стать участником космической программы, или купить билет в качестве космического туриста. Если у вас имеются неполадки со здоровьем, вам много лет, а физическая форма хромает – то выход заключается только в приобретении места в шатле.
Развивая подобную мысль, трудясь над созданием решений, проводя анализ данных, вы занимаетесь развитием аналитического образа мысли. Если вам не охота тратить время зря, то планируйте бизнес, приобретение машины или дома. Проводите анализ ситуации, думайте, что вам потребуется для реализации.
Создано немало игр и специальных тренажеров для развития логики и умения анализировать. Встречаются задачи, которые направлены на поиски оптимальных решений, восстановления цельной картины на основе нескольких деталей.
Пища для мозга
В ходе развития аналитического мышления важно обратить внимание и на питание. Существует пища для мозга, которая помогает работе главного органа организма, стимулирует его работу. Тем более, что умственный труд всегда требует немало затрат энергии, а эти затраты важно восполнять правильно. Мозгу требуется много глюкозы. К другим продуктам, которые улучшают работу мозга, относятся:
разные виды орехов;
шоколад, но только горький;
сухофрукты;
ягоды (черника, клюква);
лимон;
свекла;
шпинат;
рыбы из семейства лососевых;
белокочанная капуста.
Кроме того, для нормальной работы организма, и мозга в том числе, требуются минералы и витамины. В первую очередь, нам нужны: бор, кальций, магний, цинк, железо. Важно следить за питанием, соблюдать баланс. Это поможет мозгу правильно работать и воспринимать информацию. Замените сахар полноценными углеводами, употребляйте больше белка, как можно меньше жиров.
Кому важны аналитические способности
Чтобы понять, кому важны аналитические способности, достаточно просмотреть объявления на сайтах по поиску работы от работодателей. В них указаны основные требования к кандидатам. Почти все компании желают видеть работника, который обладает умением организовывать свое время, гибкостью мышления, аналитическим складом ума.
Аналитики ценятся в следующих профессиях:
Эксперты по отбору кандидатов отмечают, что аналитическое мышление непременный атрибут людей, которые каждый день обрабатывают огромные объемы данных. Их роль – делать прогнозы, проводить анализ, рассматривать разные ситуации и варианты.
Подобный склад ума подразумевает под собой работу с немалым объемом бумаг (накладные, договора, отчеты) или программами на ПК. Редко аналитики работают с людьми.
Если вы не уверены в том, какой у вас склад ума, то в Сети есть немало специальных тестов. После их прохождения вы увидите собственный результат и поймете, в какую сторону требуется развиваться.
3 признака, что вы станете хорошим программистом
Эксперты компаний Acronis, КРОК, Mercaux Inc., «СТРИМ», ICL Services и Bell Integrator рассказали, по каким признакам определяется «предрасположенность» к программированию. Что же делает вас потенциальным разработчиком?
У Вас математический склад ума
«По своей сути программирование очень похоже на „инженерные специальности“, человек с „математическим складом ума“ может с одинаковым успехом заниматься проектированием колесных машин либо написанием кода. Если из этого исходить, то один из главных признаков того, что у человека есть талант к программированию — это наличие аналитического склада ума, то есть склонности к изучению, анализу и выстраиванию в „законченные формы“ любой информации, которую он получает»
— говорит Антон Енакиев, Вице-президент Acronis по разработке.
«Нужно дружить с математикой, как говорил один русский ученый, „она ум в порядок приводит“»
— соглашается Сергей Стрелков, руководитель направления собственных разработок компании КРОК.
Любимый вопрос новичков или «насколько программисту нужно знать математику?»
«„Математический склад ума“ в контексте программирования вовсе не синонимичен типичному представлению об „ученом-математике“, которых обычно изображают в фильмах. Программист — это не Рассел Кроу в роли нобелевского лауреата Джона Нэша, погруженный в цифры и постоянную аналитику. В 90-95% своей работы программисты используют только базовый математический аппарат, и лишь в 5-10% задач необходимы глубокие знания математики. Поэтому, мне кажется, что нет особого требования к наличию чересчур глубоких познаний в теории графов или теории вероятности для программиста, но это всегда будет считаться плюсом»
— считает Антон Енакиев, Вице-президент Acronis по разработке.
Какая именно нужна математика рассказывает Алексей Светлов, руководитель отдела разработки технического департамента ООО «Стрим»:
«Основа программирования — дискретная математика. И хороший программист должен любить и понимать этот предмет. Это база для развития. Математика дисциплинирует человека и учит искать рациональный выход из любого положения. Иначе любая нестандартная ситуация поставит программиста в тупик и он, не найдя ответа на всех известных ресурсах, сложит руки и распишется в своей беспомощности».
«Можно не знать досконально теорию вероятностей и высшую математику, но линейная алгебра должна быть неотъемлемой частью мышления в решении большинства задач или „записана на подкорке мозга“ (как говорят некоторые учителя) — это врожденная грамотность, но в математическом смысле»
— считает Воротников Денис, ведущий веб-программист Mercaux Inc.
«Хороший программист должен быть ленивым, — так говорил один наш преподаватель в университете. И это правда! Потому что, чем меньше программного кода выполняет поставленную задачу, тем обычно гениальнее он написан. А ленивому программисту лень писать много кода — он будет искать способ, как сделать меньше работы с тем же результатом»
— объясняет Алексей Светлов, руководитель отдела разработки технического департамента ООО «Стрим».
Вы любите решать нестандартные задачи
«Не стоит забывать и о том, что программирование в большой мере творческая профессия. Несмотря на всю четкость алгоритмов и следованию гайдлайнам (правила программирования на каком-либо языке), специалисту этой профессии очень часто приходится придумывать гармоничные решения для реализации нестандартных задач. Стоит учесть, что речь идет о специалистах, разрабатывающих современные программные продукты для широкого круга пользователей, потому как в некоторых областях есть специфика, которая требует четкого следования определенным правилам и где нет места творческому подходу — например, низкоуровневое программирование на языках, близких к базовым»
— объясняет Воротников Денис, ведущий веб-программист Mercaux Inc.
Альтернативный экспресс-тест на склонность к программированию
А вы сможете создать алгоритм приготовления яичницы, не только в «идеальных» условиях, но и придумать несколько успешных альтернативных вариантов, а также создать алгоритм приготовления при исключительных, ошибочных исходных условиях?
«Если человек сможет расписать по шагам как приготовить яичницу, указав не только happy путь, а так же exceptional и alternative, тогда точно сможет стать программистом»
— утверждает Николай Каштанов, ИТ-эксперт ICL Services по предоставлению сервиса.
Если говорить о личностных качествах, то Федор Зубарев, руководитель программ компании Bell Integrator считает, что чаще всего эти два типа людей потенциально могут стать хорошими программистами:
«1-й: дотошные, пунктуальные, иногда занудные. Люди, готовые разбираться с любой мелочью, вникающие во все детали.
2-й: люди творческие, немного неаккуратные в различных, в том числе и в бытовых, вопросах. Образование — профильное или чисто математическое»
Узнаете себя в одном из типов?
Разумеется, главный тест — это ваше искреннее желание обучаться и увлеченность программированием. Только это позволит достичь результата, какими бы впечатляющими не были ваши «исходные» задатки.
«Уверен, что добиться успеха в том или ином виде деятельности можно только упорным трудом, который всегда приносит должное вознаграждение. Разработка софта — не исключение. Если такая работа продолжает радовать, если хочется еще что-то поделать „для себя“ — поисследовать, изучить что-то новое — признаки таланта налицо.»
— убежден Сергей Стрелков, руководитель направления собственных разработок компании КРОК.
Поэтому не забывайте, что при умножении любого числа на ноль, мы получаем ноль — то есть, какими бы феноменальными ни были ваши задатки, без усердной работы результата не будет. Талант необходимо развивать.
ну, на одну треть я программист, жаль только что на вторую.
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
— выводит 1, только если w входит в язык L;
— для любого w в языке L существует такое c, что V(w,c) = 1.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
— функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
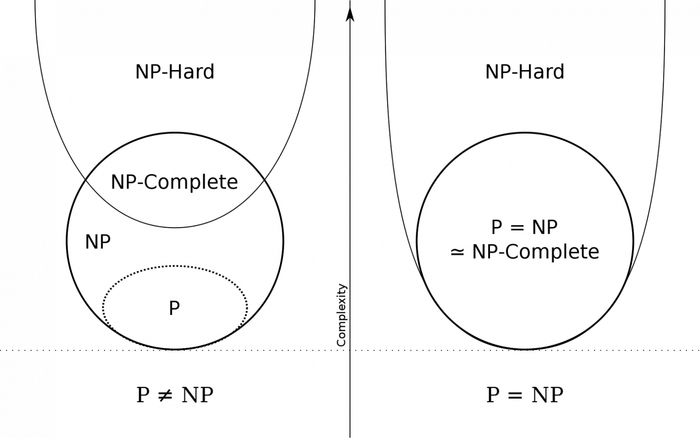
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.