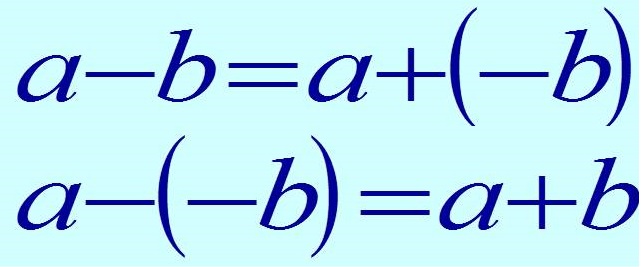что означает вычитание отрицательных чисел
Сложение и вычитание отрицательных и положительных чисел — правило, формулы и примеры
Впервые знакомство с отрицательными числами происходит в школьном курсе в 6 классе, иногда раньше. Число со знаком «+» называется положительным, противоположное — отрицательным.
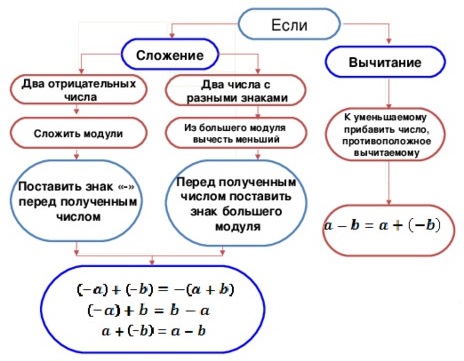
Правило сложения отрицательных чисел и чисел с разными знаками
Для суммирования двух отрицательных чисел, необходимо:
суммировать их модули;
перед полученной суммой поставить знак «минус».
В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.

Сложение рациональных или дробных чисел выполняется аналогичным способом:
К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».
Для суммирования натуральных чисел со знаками «+» и «-», надо:
из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.
Как вычитать отрицательные и положительные числа
Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
Наглядно данное действие лучше представить в виде формулы:
То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.
15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;
Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».
Заключение
Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.
Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.
Рассмотрим еще одно задание.
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150 1 Сложить их модули, а перед результатом поставить знак «плюс»
Правило сложения отрицательных чисел и чисел с разными знаками
Для суммирования двух отрицательных чисел, необходимо:
суммировать их модули;
перед полученной суммой поставить знак «минус».
В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.
Сложение рациональных или дробных чисел выполняется аналогичным способом:
К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».
Для суммирования натуральных чисел со знаками «+» и «-», надо:
из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.
Как вычитать отрицательные и положительные числа
Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
Наглядно данное действие лучше представить в виде формулы:
То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.
Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».
Заключение
Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.
Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.
Вычитание отрицательных чисел – правило (6 класс, математика)
Вычитание отрицательных чисел сложный в психологическом плане процесс: ведь требуется уменьшать изначально маленькое число, примерно такие же проблемы могут возникать при рассмотрении действий с десятичными и обычными дробями. При этом никаких сложных нюансов в этом вопросе нет. Чтобы избежать ошибок рассмотрим вычитание отрицательных чисел во всех подробностях.
Вычитание
Что такое вычитание? Фактически это уменьшение некоторого числа. Причем не всегда уменьшение оканчивается на отметке нуля. То есть, может получиться и отрицательное число, и ноль. Не стоит пугаться этого.
В начальной школе детям прививают мысль о том, что отрицательный результат заведомо неправильный. Это, само собой, миф. Но этот миф въедается в подкорку мозга и затрудняет дальнейшее изучение курса математики 5 и 6 класса. Поэтому от ощущений неправильности при получении отрицательных результатов нужно избавляться путем решения большого количества примеров с самыми разными результатами.
В математике принято говорить, что вычитание есть процесс переноса числа влево по числовой прямой. Левее может оказаться любое значение: положительное, отрицательное, ноль, целое или дробное. Единственный результат, который получиться не может, это иррациональное число. Причем последнее при условии вычитания рациональных чисел.
Отрицательные числа
Теперь обратим внимание на отрицательные числа. Отрицательным числом считается любое число меньше нуля. Причем в примерах на вычитание речь, чаще всего, идет о рациональных числах.
Если перед вами вычитание корней, то придется пользоваться приближенными вычислениями. С этим ничего не поделать: крайне редко получается выполнить вычисление в точности.
На практике это иногда необходимо, но при записи единицу просто не пишут. Так и получается знак минус при отрицательном числе.
По этому принципу работает правило знаков, которое гласит:
Кажется, что речь идет только об умножении, но деле это не совсем так:
-6-(-18)=-6-1*(-1)*18=-6+18=12 – вот так это правило выглядит в развернутой форме применительно к операциям вычитания.
Вычитание отрицательных чисел
В вычитании отрицательных чисел ничего сложного нет: правила те же, что и для вычитания положительных или любых других рациональных чисел. Нужно только правильно пользоваться правилом знаков.
Именно для того, чтобы не допускать ошибок при использовании этого правила на практике, рассмотрим все возможные ситуации вычитания отрицательных чисел.
-5-18=-1*(5+18)=-1*23=-23 – то есть, выносится общий множитель, числа складываются по модулю, а потом знак минуса возвращается. При решении число 1 принято не прописывать для сокращения записи
Вообще-то вычитание это часть операции, которую называют математической или арифметической суммой.
Что мы узнали?
Мы поговорили об отрицательных числах. Еще раз повторили основные правила вычитания и в отдельности привели правила вычитания отрицательных чисел. Для того, чтобы не допускать ошибок в дальнейшем рассмотрели все случаи подобного вычитания.
Математика
Урок 4: Вычитание отрицательных чисел
Вычитание
В 7 веке индийский математик и астроном Брахмагупта известной касты брахманов (просвещенных), которая сохранилась и до наших времен, изложил правила сложения и вычитания чисел с разными знаками. Он назвал положительные числа «доход», а отрицательные – «расход».
Брахмагупта излагал свои правила так:
Если говорить современным математическим языком, то первое правило можно прочесть так: имущество – это положительное число, поэтому сумма двух положительных чисел есть число положительное.
Долг — это отрицательное число. Поэтому второе правило можно сформулировать так: «Сумма двух отрицательных чисел есть число отрицательное».
И сформулируем третье правило: «Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший, и перед полученной разностью поставить знак числа, модуль которого больше».
Правило можно дополнить, указав, что же получается: имущество или долг. Если имущество больше долга, то получится имущество. Если имущество меньше долга, то получится долг.
Таким образом, вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому.
Например, 8-3 = 11 и потому 11-8 = 3, а также 11+(-8) = 3.
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.
Разность двух чисел положительна, если уменьшаемое больше вычитаемого, и отрицательна, если уменьшаемое меньше вычитаемого. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.
Пример 1. Чему равна длина отрезка АВ, если А(-5) и В(6)?
Значит, длина отрезка АВ равна 11 единичным отрезкам.
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
Пример 2. Найдем длину отрезка АВ, если А(1), В(4).
Пример 3. Найдем длину отрезка АС, если А(-2) и С(4).