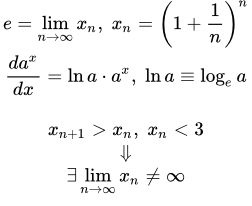Экспонента число чему равно

Что такое Экспонента

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Источник

Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е»‎ ‎– это число Эйлера, которое представляет собой постоянную (

2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.

Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).

Экспонента в жизни. Экспоненциальный рост

Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.

Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.

Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.

Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.

Чем экспоненциальный рост отличается от линейного?

Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.

В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.

При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.

Источник

Число Эйлера (e)

Число e (или, как его еще называют, число Эйлера) – это основание натурального логарифма; математическая константа, являющаяся иррациональным числом.

Способы определения числа e (формула):

1. Через предел:

Второй замечательный предел:

Альтернативный вариант (следует из формулы Муавра – Стирлинга):

2. Как сумма ряда:

Свойства числа e

1. Предел обратного числа e

2. Производные

Производной экспоненциальной функции является экспоненциальная функция:

Производной натуральной логарифмической функции является обратная функция:

3. Интегралы

Неопределенный интеграл натуральной логарифмической функции log_e x:

Определенный интеграл от 1 до e обратной функции 1/x равен 1:

Логарифмы с основанием e

Натуральный логарифм числа x определяется как базовый логарифм x с основанием e:

Экспоненциальная функция

Это показательная функция, которая определяется следующим образом:

Формула Эйлера

Комплексное число e iθ равняется:

Источник

Число е

Как легко запомнить год рождения Льва Толстого? Вспоминаем первые десять цифр числа е = 2,718281828… Там год его рождения повторяется дважды. 1828 1828. Видимо, специально, чтобы каждый знал, когда родился Великий русский писатель!

Ну а если вы вдруг позабыли, чему равны углы в прямоугольном равнобедренном треугольнике, не проблема. Сразу после дважды Толстого в числе е идет 459045.

Для забывчивых юристов далее спрятался номер статьи из ук Рф «Незаконное осуществление медицинской деятельности или фармацевтической деятельности», в общем, 235 статья.

Сколько градусов в окружности? Смотрим после 235 статьи и видим 360.

Так можно продолжать до бесконечности. Почему? Потому что число е, как и число Пи, иррациональное. Бесконечная, не периодическая, десятичная дробь. Так что в числе е есть не только год рождения Толстого, но и день месяц, и вся война и мир в цифровом виде.

Что же такое число е и откуда оно взялось?

Кто-то спросит: «Что же это за число такое удивительное?» И здесь всего три слова: “второй замечательный предел”. На языке математики это выглядит следующим образом:

Появление числа е связывают с Якобом Бернулли, который еще в 17 веке задался вопросом: какова же максимальная величина процентного дохода при постоянной капитализации вклада?

Якоб Бернулли (1654-1705)

Чтобы было понятно о чем идет речь, давайте представим, что у меня есть рубль. Я кладу его в банк под 100% годовых. То есть, через год у меня уже не рубль, а два.

Но что если рост происходит не мгновенно в конце года, а частями? Ну скажем, каждые полгода по 50%. Да, наш рубль так же превратится в два, но на 50 копеек, которые набежали за первые полгода, за вторую половину года набежит уже свой процент. И мы получим еще 25 копеек дополнительно. И в итоге мы имеем уже 2 рубля 25 копеек.

Если рост вклада будет происходить каждые четыре месяца, то есть 3 раза в год, дополнительный процент к нашим двум рублям, составит уже 37 копеек.

При ежемесячном росте только на процентах у нас набежит примерно 61 копейка.

И здесь возникает вопрос: а что если рост будет происходить непрерывно? Как в природе. К примеру, дети не вырастают на 15 сантиметров в свой день рождения. Нет. Они растут в течении всего года. Каждый день, каждый час, каждую секунду… Что если так же будет расти наш вклад, и вместе с ним будут увеличиваться начисления по проценту?

Существует ли какой то предел при непрерывном росте, который позволит понять, на какую максимальную прибыль мы можем рассчитывать?

Сам Бернулли определил, что это где-то между 2,5 и 3.

Леонард Эйлер (1707 – 1783)

Более точно этот предел вычислил Леонард Эйлер, а полученное число, к которому этот предел стремится, назвал числом е.

По одной из версий е — это первая буква в фамилии ученого (Euler). Но это не точно. Вполне возможно, что е это просто первая буква в слове«экспоненциальный» (exponential). Что тоже кажется тоже вполне разумным, так как экспонента, наверно, первая ассоциация при упоминании числа е. По крайней мере, у меня.

Экспонента

Для тех, кто не знает, экспонента — это функция:

И она, пожалуй, вызывает куда больший интерес, чем само число е. Хотя бы потому, что производная от этой функции равна самой этой функции.

А если еще вспомнить, что интегрирование — это обратный процесс к дифференцированию, не нужно иметь семь пядей во лбу, чтоб догадаться, что интеграл от e^x так же будет равен e^x.

Но не будем сильно углубляться в математику, а чтобы понять как этим всем пользоваться, ответим на несколько простых вопросов:

Что если мы вкладываем не один рубль, а два?

Число е показывает максимально возможное значение роста единичного вклада при непрерывной капитализации. То есть, если перевести на человеческий язык, с одного рубля при 100% годовых максимум за год набежит е рублей. Если изначальный вклад будет в двое больше, то максимум который мы можем получить через год тоже будет вдвое больше. 2е. Ну или 1000е если положить 1000 рублей.

— то что было.

— то что будет.

Что будет через 2-3 года?

Здесь тоже нет ничего сложного, эти 2-3 года уйдут в степень над числом (t — время).

Мы говорили, что набегает у нас с единичного вклада, соответственно, в начале следующего года у нас на счету уже рублей. Соответственно, вклад в начале второго года у нас уже не единичный. А как мы считаем рост, если вклад не единичный? Умножаем на величину этого вклада. То есть на . В конце второго года у нас на счету или рублей, через 3 года … И так далее.

Ну, а если мы имеем дело не со 100%, а скажем 10%?

Проценты в виде постоянной роста () также идут в степень. при 100% соответственно, при 10%.

Почему так происходит? Если не углубляться в математику, то можно сказать, что рост за год при 10% годовых будет такой же, как при 100% годовых за года. Ну а время у нас уходит в степень.

Все сказанное можно обобщить и представить в виде формулы:

Причем использовать эту формулу вы можете не только в области финансов. С ее помощью можно спрогнозировать рост населения в нашей необъятной Родине, рассчитать сколько радиоактивного радия останется в Вашем шкафу через год, если предварительно положить туда 10 грамм. Даже можно с легкостью определить когда от этого радия останется ровно половина.

Закон радиоактивного распада

По поводу десяти грамм радия в шкафу я конечно пошутил, но, так или иначе, закон радиоактивного распада можно представить в виде следующего уравнения:

Если решите считать радиоактивные атомы не в штуках, а в привычных килограммах и граммах.

Где — изначальная масса радиоактивного вещества, — то что останется спустя время . На, а — это постоянная распада (статистическая вероятность распада атома за единицу времени). Обратите внимание на минус в степени над числом . Минус будет говорить нам о том что количество радиоактивного вещества будет убывать.

Хотя чаще всего в учебниках вы можете встретить другое уравнение:

Здесь — это так называемый период полураспада, время за которое распадается половина радиоактивного вещества.

Половина это когда . А если вспомнить что такое натуральный логарифм () и зачем он нам нужен, то можно из первого уравнения выразить период полураспада через радиоактивную постоянную:

В общем можете вооружиться ручкой, бумагой и на досуге из этого:

Ну а если из всего сказанного вы не поняли ровным счетом ничего. И как говорил Виктор Степанович Черномырдин: «Всё это так прямолинейно и перпендикулярно, что мне неприятно». Не расстраивайтесь, по крайней мере, теперь Вы знаете как легко запомнить в каком году родился Лев Николаевич Толстой.

Источник

Число e – его смысл и доказательство сходимости последовательности

Определение числа e

Этот предел является частным случаем второго замечательного предела. Число e иногда называют числом Эйлера или числом Непера. Это самое используемое число в математическом анализе. Оно примерно равно
.
Число e можно представить в виде ряда:
.

Далее приводится объяснение, почему оно так популярно в математике, и дается доказательство существования конечного предела (1).

Смысл числа e

Таким образом, смысл применения числа e заключается в том, что через него выражается производная показательной функции, и без него просто нельзя обойтись.

Доказательство сходимости последовательности

Здесь мы покажем, что последовательность с общим членом
(2)
имеет конечный предел. Для этого мы применим теорему Вейерштрасса о пределе монотонной последовательности. Тогда нам нужно доказать, что
1) последовательность (2) монотонна;
2) последовательность (2) ограничена.

Доказательство можно выполнять различными способами.

Применение бинома Ньютона

Отсюда получаем ограниченность :
.

Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.

Применение неравенства Бернулли

Итак, мы показали, что последовательность монотонна и ограничена. Тогда по теореме Вейерштрасса, она имеет конечный предел.

Использование вспомогательной последовательности

Для исследования сходимости исходной последовательности, иногда бывает удобно взять вспомогательную последовательность, которую легче исследовать. При этом предел исходной последовательности должен выражаться через предел вспомогательной.

Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.

Элементы исходной последовательности выражаются через :
.
Далее замечаем, что
.
Применяем теорему о пределе частного числовой последовательности:
.
Поскольку последовательность имеет конечный предел, то и исходная последовательность имеет конечный предел.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник