Экстремум функции что это
Что такое экстремумы функции: критические точки максимума и минимума
Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
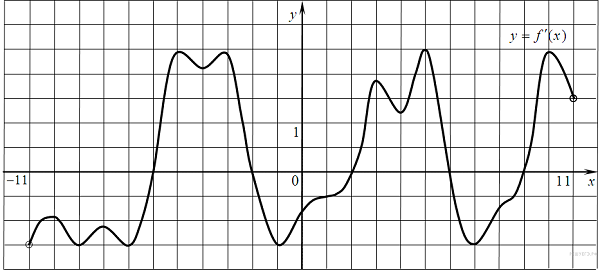
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения. В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством
Острый экстремум
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
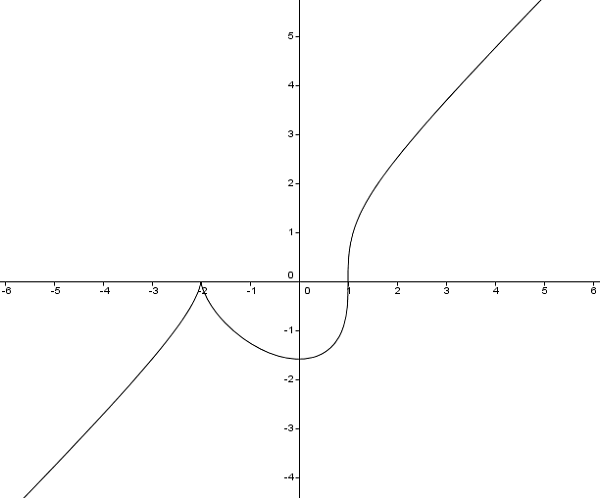
Экстремальное значение функции
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
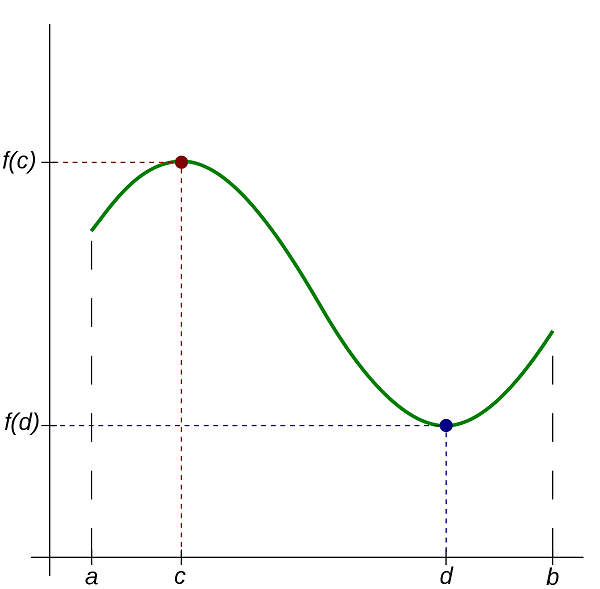
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
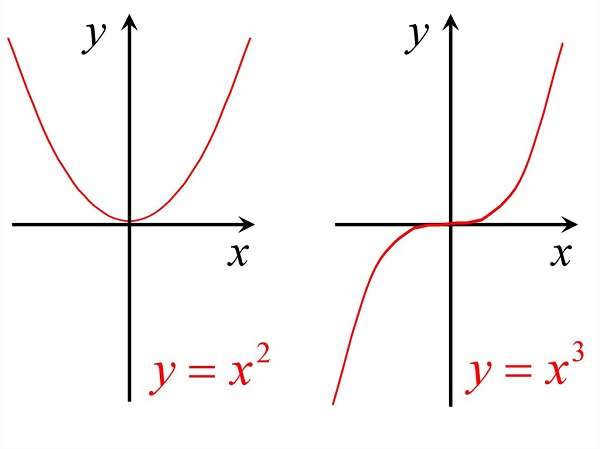
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
| Полное исследование значения | Построение графика значения |
| 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3. Процесс определения изменений положения на графике. 4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5. Создание сводной таблицы исследования с точки зрения определения ее координат. 6. Нахождение промежутков возрастания и убывания крайних и острых точек. 7. Определение выпуклости и вогнутости кривой. 8. Построение графика с учетом исследования позволяет найти минимум либо максимум. | Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике. Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума. Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума. Экстремум функционалаДля того чтобы отыскать вышеозначенное значение, необходимо придерживаться следующих правил: Используются также такие понятия, как слабый минимум и сильный минимум. Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Экстремумы функции. 10 класс. Исследование функции. Экстремумы функции bezbotvy ВыводПосле прочтения и осознания данной статьи любой новичок в математике имеет возможность понять возможности острых экстремумов в том виде, в каком они используются в образовательном процессе. Вышеперечисленные моменты позволяют разобраться в крайних точках без помощи репетиторов. Алгебра и начала математического анализа. 11 классКонспект урокаАлгебра и начала математического анализа, 11 класс Урок № 16. Экстремумы функции. Перечень вопросов, рассматриваемых в теме 1) Определение точек максимума и минимума функции 2) Определение точки экстремума функции 3) Условия достаточные для нахождения точек экстремума функции Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, Максимум функции. Значение функции в точке максимума называют максимумом функции Минимум функции. Значение функции в точке минимума называют минимумом функции Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке). Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство Точки экстремума функции. Точки минимума и максимума называют точками экстремума. Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, Алгоритм исследования функции на монотонность и экстремумы: 1) Найти область определения функции D(f) 3) Найти стационарные (f'(x) = 0) и критические (f'(x) не существует) точки функции y = f(x). 4) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся 5) Сделать выводы о монотонности функции и точках ее Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011. Теоретический материал для самостоятельного изучения Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА. Точки максимума и минимума – точки экстремума. Функция может иметь неограниченное количество экстремумов. Критическая точка – это точка, производная в которой равна 0 или не существует. Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной. Алгоритм нахождения максимума/минимума функции на отрезке: Примеры и разбор решения заданий тренировочного модуля Решение: Найдем производную заданной функции: у’=2x-8 Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4) Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4) №2. Найдите точку минимума функции у= 2х-ln(х+3)+9 Решение: Найдем производную заданной функции: Найдем нули производной: Определим знаки производной функции и изобразим на рисунке поведение функции: Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени. V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 м\c №4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна. Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3 Возрастание и убывание функции на интервале, экстремумыЧтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала. Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной. Возрастание и убывание функции на интервалеТочки экстремума, экстремумы функцииОкрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже. Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже. Достаточные условия возрастания и убывания функцииЧтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак. Первое достаточное условие экстремумаИначе говоря, получим их условия постановки знака: Алгоритм для нахождения точек экстремумаЧтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения: Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции. Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума. Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида: После чего необходимо найти производную: Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что: Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю: Изображение на прямой имеет вид Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что Перейдем к вычислению минимумов: Произведем вычисления максимумов функции. Получим, что Второй признак экстремума функцииДля начала находим область определения. Получаем, что Необходимо продифференцировать функцию, после чего получим Третье достаточное условие экстремумаИсходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции. Возрастание, убывание и экстремумы функцииА сегодня в воздухе витает дух редкого единодушия, и я прямо чувствую, что все присутствующие горят желанием научиться исследовать функцию с помощью производной. Поэтому на экранах ваших мониторов незамедлительно появляется разумная добрая вечная терминология. Зачем? Одна из причин самая что ни на есть практическая: чтобы было понятно, что от вас вообще требуется в той или иной задаче! Монотонность функции. Точки экстремума и экстремумы функцииРассмотрим некоторую функцию На всякий случай сразу избавимся от возможных иллюзий, особенно это касается тех читателей, кто недавно ознакомился с интервалами знакопостоянства функции. Сейчас нас НЕ ИНТЕРЕСУЕТ, как расположен график функции относительно оси Функция возрастает на интервале, если для любых двух точек этого интервала, связанных отношением Аналогично, функция убывает на интервале, если для любых двух точек данного интервала, таких, что Если функция возрастает или убывает на интервале, то её называют строго монотонной на данном интервале. Что такое монотонность? Понимайте в буквальном смысле – однообразие. Также можно определить неубывающую функцию (смягчённое условие Теория рассматривает и другие подходы к определению возрастания/убывания функции, в том числе на полуинтервалах, отрезках, но чтобы не выливать на вашу голову масло-масло-масляное, договоримся оперировать открытыми интервалами с категоричными определениями – это чётче, и для решения многих практических задач вполне достаточно. Таким образом, в моих статьях за формулировкой «монотонность функции» почти всегда будут скрываться интервалы строгой монотонности (строгого возрастания или строгого убывания функции). Окрестность точки. Слова, после которых студенты разбегаются, кто куда может, и в ужасе прячутся по углам. …Хотя после поста Пределы по Коши уже, наверное, не прячутся, а лишь слегка вздрагивают =) Не беспокойтесь, сейчас не будет доказательств теорем математического анализа – окрестности мне потребовались, чтобы строже сформулировать определения точек экстремума. Вспоминаем: Окрестностью точки называют интервал, который содержит данную точку, при этом для удобства интервал часто полагают симметричным. Например, точка Точка Точка Примечание: требование симметричности окрестности вовсе не обязательно. Кроме того, важен сам факт существования окрестности (хоть малюсенькой, хоть микроскопической), удовлетворяющей указанным условиям Точки Как понимать слово «экстремум»? Да так же непосредственно, как и монотонность. Экстремальные точки американских горок. Как и в случае с монотонностью, в теории имеют место и даже больше распространены нестрогие постулаты (под которые, естественно, подпадают рассмотренные строгие случаи!): Точка Заметьте, что согласно последним двум определениям, любая точка функции-константы (либо «ровного участка» какой-нибудь функции) считается как точкой максимума, так и точкой минимума! Функция Да, кстати, о королевских особах: Общее название – экстремумы функции. Пожалуйста, будьте аккуратны в словах! Точки экстремума – это «иксовые» значения. ! Примечание: иногда перечисленными терминами называют точки «икс-игрек», лежащие непосредственно на САМОМ ГРАФИКЕ функции. Сколько может быть экстремумов у функции? Ни одного, 1, 2, 3, … и т.д. до бесконечности. Например, у синуса бесконечно много минимумов и максимумов. ВАЖНО! Термин «максимум функции» не тождественен термину «максимальное значение функции». Легко заметить, что значение Чайникам на первых порах рекомендую создать и осмыслить небольшой терминологический конспект, чтобы не путать Иран с Ираком. Подытожим наш небольшой экскурс в теорию контрольным выстрелом: что подразумевает задание «найдите промежутки монотонности и точки экстремума функции»? Формулировка побуждает найти: – интервалы возрастания/убывания функции (намного реже фигурирует неубывание, невозрастание); – точки максимума и/или точки минимума (если таковые существуют). Ну и от незачёта подальше лучше найти сами минимумы/максимумы 😉 Как всё это определить? С помощью производной функции! Как найти интервалы возрастания, убывания, |
 из этого промежутка выполняется неравенство
из этого промежутка выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции. .
. .
. из этого промежутка выполняется неравенство
из этого промежутка выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.













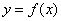 . Упрощённо полагаем, что она непрерывна на всей числовой прямой:
. Упрощённо полагаем, что она непрерывна на всей числовой прямой: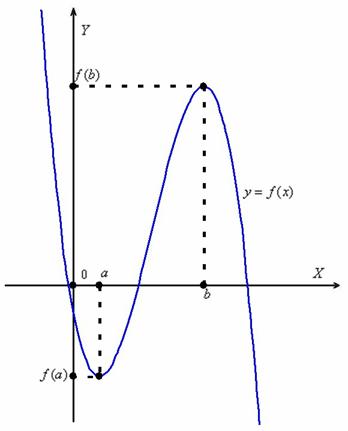
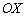 (выше, ниже, где пересекает ось). Для убедительности мысленно сотрите оси и оставьте один график. Потому что интерес именно в нём.
(выше, ниже, где пересекает ось). Для убедительности мысленно сотрите оси и оставьте один график. Потому что интерес именно в нём.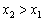 , справедливо неравенство
, справедливо неравенство 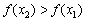 . То есть, бОльшему значению аргумента соответствует бОльшее значение функции, и её график идёт «снизу вверх». Демонстрационная функция
. То есть, бОльшему значению аргумента соответствует бОльшее значение функции, и её график идёт «снизу вверх». Демонстрационная функция 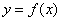 растёт на интервале
растёт на интервале 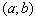 .
.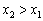 , справедливо неравенство
, справедливо неравенство 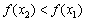 . То есть, бОльшему значению аргумента соответствует мЕньшее значение функции, и её график идёт «сверху вниз». Наша функция
. То есть, бОльшему значению аргумента соответствует мЕньшее значение функции, и её график идёт «сверху вниз». Наша функция 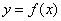 убывает на интервалах
убывает на интервалах 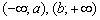 .
.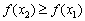 в первом определении) и невозрастающую функцию (смягчённое условие
в первом определении) и невозрастающую функцию (смягчённое условие 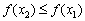 во 2-м определении). Неубывающую или невозрастающую функцию на интервале называют монотонной функцией на данном интервале (строгая монотонность – частный случай «просто» монотонности).
во 2-м определении). Неубывающую или невозрастающую функцию на интервале называют монотонной функцией на данном интервале (строгая монотонность – частный случай «просто» монотонности).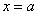 и её стандартная
и её стандартная 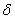 — окрестность:
— окрестность: 
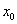 называется точкой строгого максимума, если существует её
называется точкой строгого максимума, если существует её 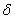 -окрестность, для всех значений
-окрестность, для всех значений 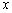 которой за исключением самой точки
которой за исключением самой точки 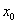 выполнено неравенство
выполнено неравенство 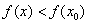 . В нашем конкретном примере это точка
. В нашем конкретном примере это точка 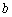 .
.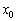 называется точкой строгого минимума, если существует её
называется точкой строгого минимума, если существует её 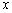 которой за исключением самой точки
которой за исключением самой точки 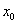 выполнено неравенство
выполнено неравенство 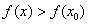 . На чертеже – точка «а».
. На чертеже – точка «а».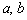 называют точками строго экстремума или просто точками экстремума функции. То есть это обобщенный термин точек максимума и точек минимума.
называют точками строго экстремума или просто точками экстремума функции. То есть это обобщенный термин точек максимума и точек минимума.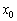 называется точкой максимума, если существует её окрестность, такая, что для всех значений
называется точкой максимума, если существует её окрестность, такая, что для всех значений 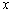 данной окрестности выполнено неравенство
данной окрестности выполнено неравенство 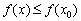 .
. 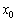 называется точкой минимума, если существует её окрестность, такая, что для всех значений
называется точкой минимума, если существует её окрестность, такая, что для всех значений 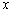 данной окрестности выполнено неравенство
данной окрестности выполнено неравенство 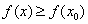 .
.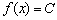 , к слову, одновременно является и невозрастающей и неубывающей, то есть монотонной. Однако оставим сии рассуждения теоретикам, поскольку на практике мы почти всегда созерцаем традиционные «холмы» и «впадины» (см. чертёж) с уникальным «царём горы»
, к слову, одновременно является и невозрастающей и неубывающей, то есть монотонной. Однако оставим сии рассуждения теоретикам, поскольку на практике мы почти всегда созерцаем традиционные «холмы» и «впадины» (см. чертёж) с уникальным «царём горы» 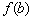 или «принцессой болота»
или «принцессой болота» 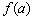 . Как разновидность, встречается остриё, направленное вверх либо вниз, например, минимум функции
. Как разновидность, встречается остриё, направленное вверх либо вниз, например, минимум функции 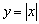 в точке
в точке 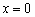 .
.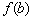 называют максимумом функции;
называют максимумом функции; 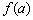 называют минимумом функции.
называют минимумом функции.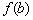 максимально лишь в локальной окрестности, а слева вверху есть и «покруче товарищи». Аналогично, «минимум функции» – не то же самое, что «минимальное значение функции», и на чертеже мы видим, что значение
максимально лишь в локальной окрестности, а слева вверху есть и «покруче товарищи». Аналогично, «минимум функции» – не то же самое, что «минимальное значение функции», и на чертеже мы видим, что значение 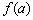 минимально только на определённом участке. В этой связи точки экстремума также называют точками локального экстремума, а экстремумы – локальными экстремумами. Ходят-бродят неподалёку и глобальные собратья. Так, любая парабола имеет в своей вершине глобальный минимум или глобальный максимум. Далее я не буду различать типы экстремумов, и пояснение озвучено больше в общеобразовательных целях – добавочные прилагательные «локальный»/«глобальный» не должны заставать врасплох.
минимально только на определённом участке. В этой связи точки экстремума также называют точками локального экстремума, а экстремумы – локальными экстремумами. Ходят-бродят неподалёку и глобальные собратья. Так, любая парабола имеет в своей вершине глобальный минимум или глобальный максимум. Далее я не буду различать типы экстремумов, и пояснение озвучено больше в общеобразовательных целях – добавочные прилагательные «локальный»/«глобальный» не должны заставать врасплох.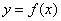 . Тогда:
. Тогда: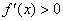 на интервале, то функция
на интервале, то функция 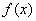 возрастает на данном интервале;
возрастает на данном интервале;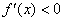 на интервале, то функция
на интервале, то функция 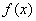 убывает на данном интервале.
убывает на данном интервале.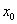 принадлежит области определения функции
принадлежит области определения функции 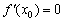 либо значения
либо значения 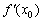 не существует. Критическая точка может быть точкой экстремума. А может и не быть. Очень скоро мы рассмотрим необходимые и достаточные условия существования экстремума.
не существует. Критическая точка может быть точкой экстремума. А может и не быть. Очень скоро мы рассмотрим необходимые и достаточные условия существования экстремума.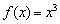 неотрицательна:
неотрицательна: 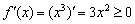 для любого «икс».
для любого «икс». 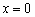 скорость изменения функции равна нулю, о чём в рупор кричит производная:
скорость изменения функции равна нулю, о чём в рупор кричит производная: 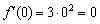 . И вот вам, кстати, сразу пример, когда в критической точке нет максимума или минимума функции.
. И вот вам, кстати, сразу пример, когда в критической точке нет максимума или минимума функции.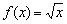 обитает на промежутке
обитает на промежутке 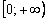 , а её производная неравенством
, а её производная неравенством 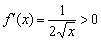 однозначно показывает, что «корень из икс» строго растёт на интервале
однозначно показывает, что «корень из икс» строго растёт на интервале 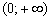 В критической точке
В критической точке 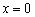 функция определена, но не дифференцируема.
функция определена, но не дифференцируема. 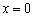 не является точкой минимума функции
не является точкой минимума функции 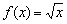 (хотя «по понятиям» это вроде бы так). Дело в том, что определения точек максимума и минимума предполагают существование функции
(хотя «по понятиям» это вроде бы так). Дело в том, что определения точек максимума и минимума предполагают существование функции 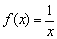 идёт «сверху вниз», то есть данная функция убывает на всей области определения. Что и показывает её производная:
идёт «сверху вниз», то есть данная функция убывает на всей области определения. Что и показывает её производная: 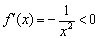 для любого «икс» кроме нуля.
для любого «икс» кроме нуля. 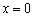 вообще не считается критической, так как функция
вообще не считается критической, так как функция 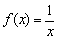 банально в ней не определена.
банально в ней не определена.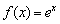 растёт на всей числовой прямой (для любого значения «икс» справедливо строгое неравенство
растёт на всей числовой прямой (для любого значения «икс» справедливо строгое неравенство 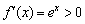 ). Исследуя же производную
). Исследуя же производную 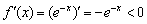 , легко сделать вывод, что функция
, легко сделать вывод, что функция 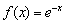 наоборот – убывает на
наоборот – убывает на 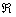 .
.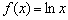
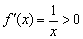 на интервале
на интервале 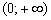 .
.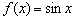 и её производной
и её производной 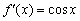 . Там, где график косинуса находится над осью
. Там, где график косинуса находится над осью 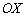 , синус растёт. Обратно – где график
, синус растёт. Обратно – где график 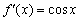 расположен ниже оси абсцисс, синус убывает. А в тех точках, где косинус пересекает ось (
расположен ниже оси абсцисс, синус убывает. А в тех точках, где косинус пересекает ось (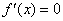 ), синусоида
), синусоида 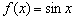 достигает минимума или максимума.
достигает минимума или максимума.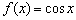 и его производной
и его производной 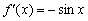 (второй кадр запечатлён в статье Геометрические преобразования графиков).
(второй кадр запечатлён в статье Геометрические преобразования графиков).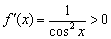 несёт бодрую весть о том, что функция
несёт бодрую весть о том, что функция 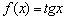 возрастает на всей области определения.
возрастает на всей области определения.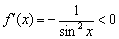 ситуация ровно противоположная.
ситуация ровно противоположная.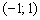 растёт – производная здесь положительна:
растёт – производная здесь положительна: 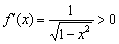 .
. 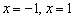 функция
функция 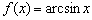 определена, но не дифференцируема. Однако в критической точке
определена, но не дифференцируема. Однако в критической точке 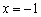 существует правосторонняя производная и правостороння касательная, а на другом краю – их левосторонние визави.
существует правосторонняя производная и правостороння касательная, а на другом краю – их левосторонние визави.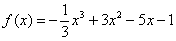
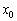 есть экстремум, то
есть экстремум, то 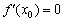 ещё не следует, что функция достигает максимума или минимума в точке
ещё не следует, что функция достигает максимума или минимума в точке 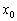 . Классический пример уже засветился выше – это кубическая парабола
. Классический пример уже засветился выше – это кубическая парабола 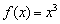 и её критическая точка
и её критическая точка 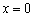 .
.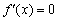 :
: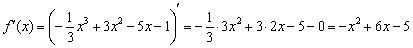
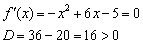
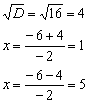
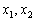 , однако в ходе полного исследования функции удобнее обойтись без подстрочных индексов, так как они вносят лишние оговорки и путаницу
, однако в ходе полного исследования функции удобнее обойтись без подстрочных индексов, так как они вносят лишние оговорки и путаницу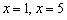 – критические точки
– критические точки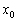 . Тогда:
. Тогда: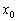 производная меняет знак с «минуса» на «плюс», то в данной точке функция достигает минимума.
производная меняет знак с «минуса» на «плюс», то в данной точке функция достигает минимума.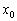 развернулся в противоположную сторону. Минимум.
развернулся в противоположную сторону. Минимум.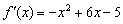 , ветви которой направлены вниз, и многим читателям уже понятны знаки производной, но ради повторения снова пройдёмся по всем этапам метода интервалов. Отложим на числовой прямой найденные критические точки:
, ветви которой направлены вниз, и многим читателям уже понятны знаки производной, но ради повторения снова пройдёмся по всем этапам метода интервалов. Отложим на числовой прямой найденные критические точки: 
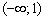 и находим значение производной в данной точке. Удобнее всего выбрать
и находим значение производной в данной точке. Удобнее всего выбрать 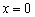 :
: 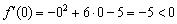 , значит, производная отрицательна на всём интервале
, значит, производная отрицательна на всём интервале 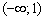 .
.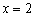 , принадлежащую интервалу
, принадлежащую интервалу 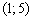 , и проводим аналогичное действие:
, и проводим аналогичное действие: 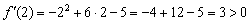 , следовательно,
, следовательно, 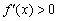 на всём интервале
на всём интервале 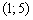 .
.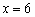 последнего интервала:
последнего интервала: 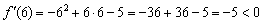 , поэтому
, поэтому 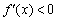 в любой точке интервала
в любой точке интервала 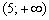 .
.
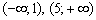 производная отрицательна, значит, САМА ФУНКЦИЯ
производная отрицательна, значит, САМА ФУНКЦИЯ 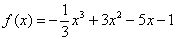 на данных интервалах убывает, и её график идёт «сверху вниз». На среднем интервале
на данных интервалах убывает, и её график идёт «сверху вниз». На среднем интервале 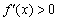 , значит, функция возрастает на
, значит, функция возрастает на 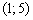 , и её график идёт «снизу вверх».
, и её график идёт «снизу вверх».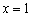 производная меняет знак с «–» на «+», следовательно, в этой точке функция достигает минимума:
производная меняет знак с «–» на «+», следовательно, в этой точке функция достигает минимума: 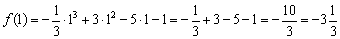
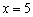 производная меняет знак с «+» на «–», и функция достигает максимума в данной точке:
производная меняет знак с «+» на «–», и функция достигает максимума в данной точке: 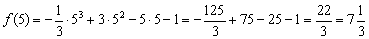
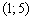 и убывает на интервалах
и убывает на интервалах 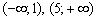 . В точке
. В точке 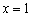 функция достигает минимума:
функция достигает минимума: 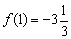 , а в точке
, а в точке 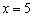 – максимума:
– максимума: 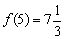
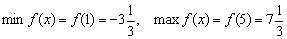 . Под значками
. Под значками 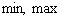 обычно понимают минимальное и максимальное значение, а это, как пояснялось выше, далеко не то же самое, что минимум и максимум.
обычно понимают минимальное и максимальное значение, а это, как пояснялось выше, далеко не то же самое, что минимум и максимум.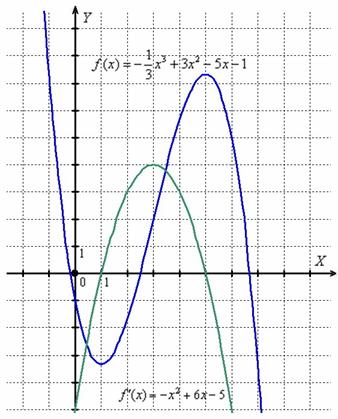
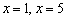 (в которых парабола пересекает ось абсцисс). Затем методом интервалов было установлено, где
(в которых парабола пересекает ось абсцисс). Затем методом интервалов было установлено, где 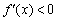 (парабола ниже оси) и
(парабола ниже оси) и 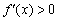 (парабола выше оси). Таким образом, с помощью производной мы узнали интервалы возрастания/убывания и экстремумы «синей» функции.
(парабола выше оси). Таким образом, с помощью производной мы узнали интервалы возрастания/убывания и экстремумы «синей» функции.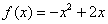 : «…берём первую производную и приравниваем ее к нулю:
: «…берём первую производную и приравниваем ее к нулю: 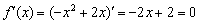 …Итак, решение нашего уравнения:
…Итак, решение нашего уравнения: 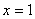 – именно в этой точке и находится вершина параболы…». Теперь, думаю, всем понятно, почему вершина параболы находится именно в этой точке =) Вообще, следовало бы начать с похожего примера и здесь, но он уж слишком прост (даже для чайника). К тому же, аналог есть в самом конце урока о производной функции. Поэтому повысим степень:
– именно в этой точке и находится вершина параболы…». Теперь, думаю, всем понятно, почему вершина параболы находится именно в этой точке =) Вообще, следовало бы начать с похожего примера и здесь, но он уж слишком прост (даже для чайника). К тому же, аналог есть в самом конце урока о производной функции. Поэтому повысим степень: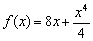
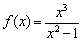
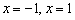 .
.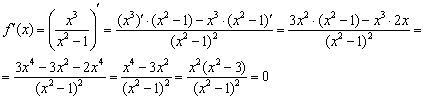
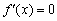 . Дробь равна нулю, когда её числитель равен нулю:
. Дробь равна нулю, когда её числитель равен нулю: 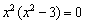
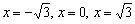

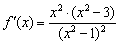 и определить её знак. Выгоднее даже не считать, а «прикинуть» устно. Возьмём, например, точку
и определить её знак. Выгоднее даже не считать, а «прикинуть» устно. Возьмём, например, точку 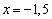 , принадлежащую интервалу
, принадлежащую интервалу 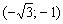 , и выполним подстановку:
, и выполним подстановку: 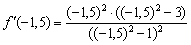 .
. 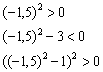
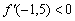 , а значит, производная отрицательна и на всём интервале
, а значит, производная отрицательна и на всём интервале 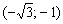 .
.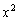 и знаменатель
и знаменатель 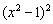 строго положительны для любой точки любого интервала, что существенно облегчает задачу.
строго положительны для любой точки любого интервала, что существенно облегчает задачу.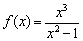 возрастает на
возрастает на 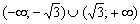 и убывает на
и убывает на 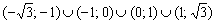 . Однотипные интервалы удобно скреплять значком объединения
. Однотипные интервалы удобно скреплять значком объединения 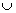 .
.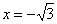 функция достигает максимума:
функция достигает максимума: 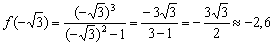
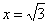 функция достигает минимума:
функция достигает минимума: 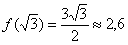
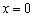 производная не меняет знак, поэтому у функции там НЕТ ЭКСТРЕМУМА – она как убывала, так и осталась убывающей.
производная не меняет знак, поэтому у функции там НЕТ ЭКСТРЕМУМА – она как убывала, так и осталась убывающей.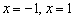 не считаются критическими – в них функция не определена. Соответственно, здесь экстремумов не может быть в принципе (даже если производная меняет знак).
не считаются критическими – в них функция не определена. Соответственно, здесь экстремумов не может быть в принципе (даже если производная меняет знак).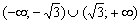 и убывает на
и убывает на 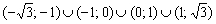 В точке
В точке 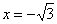 достигается максимум функции:
достигается максимум функции: 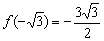 , а в точке
, а в точке 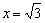 – минимум:
– минимум: 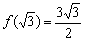 .
.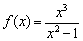 есть две вертикальные асимптоты
есть две вертикальные асимптоты 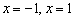 и наклонная асимптота
и наклонная асимптота 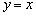 . Вот наш герой:
. Вот наш герой: 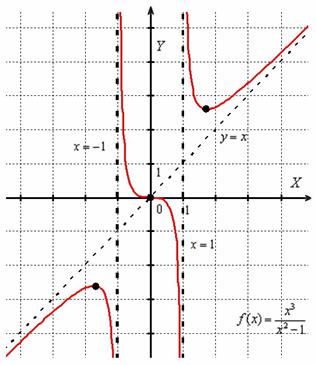
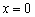 экстремума нет, но существует перегиб графика (что, как правило, и бывает в похожих случаях).
экстремума нет, но существует перегиб графика (что, как правило, и бывает в похожих случаях).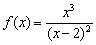
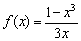
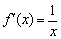 определена на интервале
определена на интервале 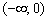 , но сам логарифм – нет. Интервалы, которые не входят в область определения функции, НЕЛЬЗЯ рассматривать и у производной!
, но сам логарифм – нет. Интервалы, которые не входят в область определения функции, НЕЛЬЗЯ рассматривать и у производной!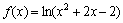
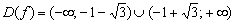 , знание которой КРИТИЧЕСКИ ВАЖНО учитывать в нашей задаче:
, знание которой КРИТИЧЕСКИ ВАЖНО учитывать в нашей задаче: 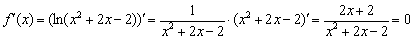
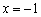 и крайние точки области определения:
и крайние точки области определения: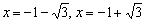 .
.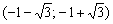 . Более того, точка
. Более того, точка 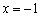 (не критическая. ;)) вошла в этот нехороший интервал! Что делать? Мама всегда права, поэтому определяем знаки производной только на интервалах области определения функции:
(не критическая. ;)) вошла в этот нехороший интервал! Что делать? Мама всегда права, поэтому определяем знаки производной только на интервалах области определения функции: 
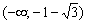 и возрастает на интервале
и возрастает на интервале 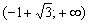 . Точки экстремума (и, понятно, экстремумы) ОТСУТСТВУЮТ. Значение
. Точки экстремума (и, понятно, экстремумы) ОТСУТСТВУЮТ. Значение 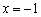 осталось не при делах, так как на интервале
осталось не при делах, так как на интервале 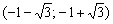 попросту нет графика функции
попросту нет графика функции 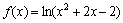 .
.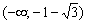 и возрастает на
и возрастает на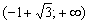 , экстремумы отсутствуют.
, экстремумы отсутствуют.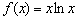
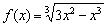
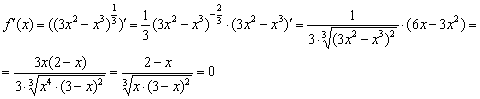
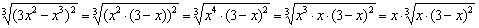 , затем сокращаем числитель и знаменатель на «икс».
, затем сокращаем числитель и знаменатель на «икс».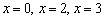 – критические точки. Почему значения
– критические точки. Почему значения 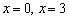 , обращающие знаменатель производной в ноль, следует отнести к критическим точкам? А дело в том, что САМА-ТО ФУНКЦИЯ в них определена! Ситуация необычна, но клубок распутывается по стандартной схеме.
, обращающие знаменатель производной в ноль, следует отнести к критическим точкам? А дело в том, что САМА-ТО ФУНКЦИЯ в них определена! Ситуация необычна, но клубок распутывается по стандартной схеме.
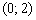 и убывает на
и убывает на 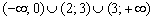 .
.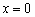 функция достигает минимума:
функция достигает минимума: 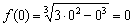 .
. 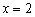 функция достигает максимума:
функция достигает максимума: 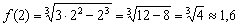 .
. 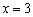 нет экстремума.
нет экстремума.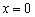 – точка минимума,
– точка минимума, 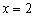 – точка максимума
– точка максимума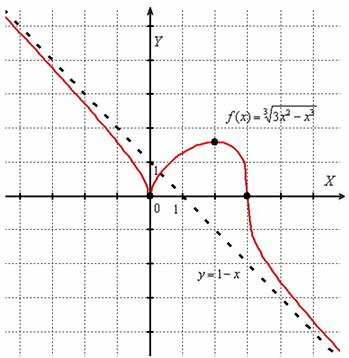
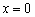 – классическое остриё, направленное вниз, при
– классическое остриё, направленное вниз, при 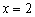 – «нормальный» максимум. В точках
– «нормальный» максимум. В точках 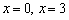 функция не дифференцируема, однако в них существуют бесконечные производные и вертикальные касательные (см. теорию производной).
функция не дифференцируема, однако в них существуют бесконечные производные и вертикальные касательные (см. теорию производной).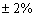 . Я проводил статистическое исследование.
. Я проводил статистическое исследование.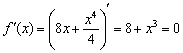
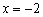 – критическая точка.
– критическая точка. 
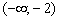 и возрастает на интервале
и возрастает на интервале 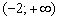 . В точке
. В точке 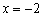 функция достигает минимума:
функция достигает минимума: 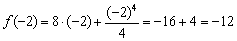
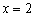 .
. 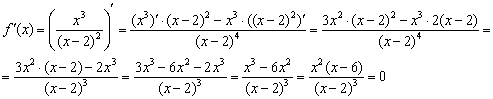
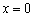 ,
, 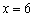 – критические точки.
– критические точки. 
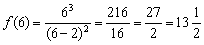 .
. 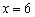 функция достигает минимума:
функция достигает минимума: 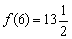
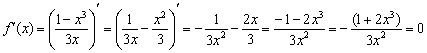
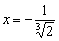 – критическая точка.
– критическая точка. 
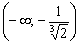 и убывает на
и убывает на 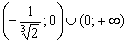 . В точке
. В точке 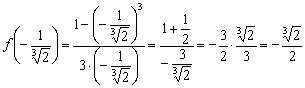
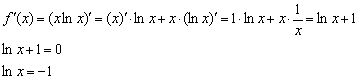
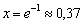 – критическая точка.
– критическая точка. 
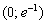 и возрастает на интервале
и возрастает на интервале 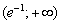 В точке
В точке 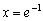 функция достигает минимума:
функция достигает минимума: 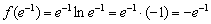
 Zaochnik.com – профессиональная помощь студентам
Zaochnik.com – профессиональная помощь студентам