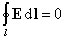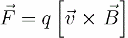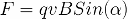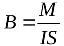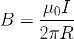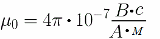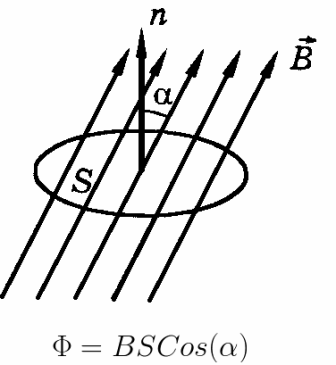
Вектор электрической индукции

Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :

Вектор электрического смещения в СНС определяется как:

Вектор индукции

Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:

Связь вектора напряженности и вектора электрического смещения

При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:

Где ε – диэлектическая проницаемость среды.

Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:

Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:

Формула тангенциальной составляющей:

Поле вектора D → изображается при помощи линий электрического смещения.

Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:

Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:

Запись результирующего поля с диэлектриком примет вид:

Формула плотности связанных зарядов:

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

Ответ: вектор электрической индукции не изменяется.

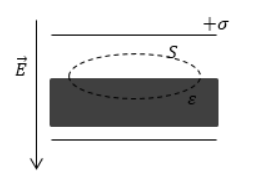
Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.

Рисунок 1 . Замкнутая поверхность

Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :

Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

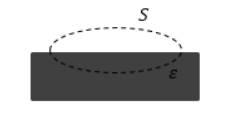
Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:

Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.

Источник

Электрическая индукция

Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами, так что вектор напряженности E, характеризующий результирующее поле в диэлектрике, является суммой двух величин, напряженности поля, создаваемого свободными зарядами Е_своб, и поля, создаваемого связанными зарядами Е_связ

. (3.6)

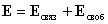
Важно понимать, что вектор поляризации Р обусловлен именно этим результирующим полем Е, то есть вектор поляризации зависит от поля, часть которого он сам же и создает. Это затрудняет его нахождение, поэтому вводят еще одну характеристику электрического поля внутри диэлектрика, которая характеризует поле одних лишь свободных зарядов.

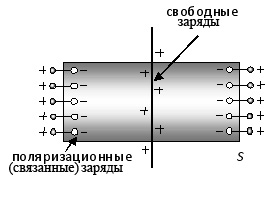
Рассмотрим ситуацию, когда электрическое поле в диэлектрике создается, к примеру, равномерно заряженной плоскостью, помещенной внутрь диэлектрика (Рис.3.6).

Для определения результирующего поля Е воспользуемся теоремой Гаусса. В качестве произвольной поверх­но­сти выберем, как в рассмотренной ранее задаче о поле заряженной плоскости, цилиндр длиной , ось ко­то­рого перпендикулярна плоскости, а основания равноудалены от нее. Теперь внутрь поверхности попадут не только свободные заряды, находящиеся на плос­ко­сти, но и связанные заряды, появля­ю­щиеся вследствие поляризации ди­элек­трической среды (на рис. 3.6 показаны диполи, «разрезанные» поверхностью на две части – отрицательные связанные заряды этих диполей оказались внутри поверхности ). Поэтому теорему Гаусса в этом случае правильно будет записать в следующем виде:

(3.7)

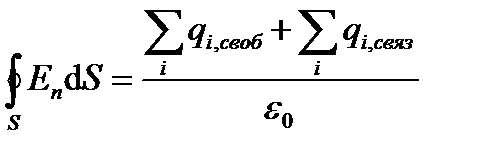
Суммы свободных и связанных зарядов в правой части уравнения можно выразить через плотности σ и σ` для свободных и связанных зарядов

(3.8)

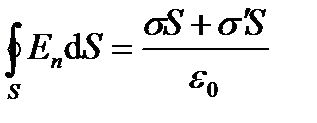
Умножим обе части этого равенства на ε_0. Кроме того, перенесем слагаемое σ`S в левую часть уравнения и внесем его под знак интеграла. Получим

(3.9)

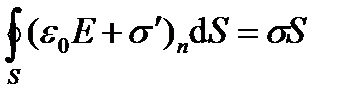
Учтем также, что как показано выше (3.3) σ` = Р. Получим

(3.10)

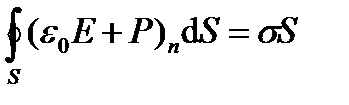
Это выражение следует трактовать так: поток некоторой векторной величины ε₀Е+Р через замкнутую поверхность S равен сумме свободных зарядов (σS), заключенных внутри этой поверхности. Эту векторную величину (ε₀Е+Р), характеризующую электрическое поле, называют электрической индукцией(D) или электрическим смещением. Итак

D = ε₀Е+Р (3.11)

Вектор электрической индукции характеризует электрическое поле только свободных зарядов (или определяется только свободными зарядами). При одном и том же распределении свободных зарядов этот вектор будет одним и тем же, независимо от среды, в которой находятся эти заряды. Вектор электрической индукции начинается и заканчивается только на свободных зарядах, поэтому линии электрической индукции не имеет разрывов на поверхностях разделяющих различные диэлектрические среды.

Единица электрического смещения — Кулон на метр в квадрате (Кл/м 2 ).

Выражение (3.10) фактически является теоремой Гаусса для вектора электрической индукции: поток вектора электрической индукции через замкнутую поверхность равен сумме свободных зарядов, заключенных внутри этой поверхности.

Подставим полученное ранее выражение (3.2) для вектора поляризации 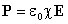в формулу (3.11)). Получим

D = ε₀(1+χ)E (3.12)

Безразмерную величину 1+χ мы уже встречали ранее (3.6). Ее называют диэлектрической проницаемостью среды ε. Таким образом

D = ε₀εE (3.13)

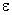
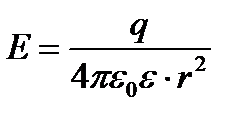
В отличие от электрической индукции напряженность электрического поля характеризует как свободные, так и связанные заряды, поэтому вектор напряженности терпит разрывы на границах областей, где присутствуют связанные заряды, например на границе раздела двух диэлектриков с различными . Часть линий напряженности Е прерывается на связанных зарядах, образующихся на границе раздела среды (см. рис. ). Поэтому напряженность поля в среде оказывается меньше, чем вне ее. Диэлектрическая проницаемость ε показывает, во сколько раз напряженность поля в среде меньше, чем в вакууме.

, (3.14)

а поле плоскости, равномерно заряженной с поверхностной плотностью σ равно

(3.15)

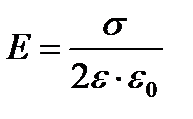
Граничные условия

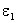
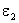
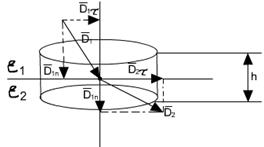
Рассмотрим поведение векторов E и D на границе раздела двух однородных изотропных диэлектриков с проницаемостями и при отсутствии на границе свободных зарядов.

Граничные условия для нормальных составляющих векторов D и E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы (рис. 3.7).

Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность

.

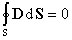
Выделяя потоки через основания и боковую поверхность цилиндра

, (3.16)

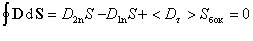
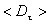
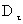
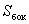
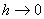
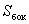
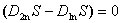
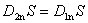
где — значение касательной составляющей усредненное по боковой поверхности . Переходя к пределу при (при этом также стремится к нулю), получаем , или окончательно для нормальных составляющих вектора электрической индукции , то есть

Для нормальных составляющих вектора напряженности поля, учитывая (3.13) получим

. (3.18)

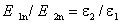
Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора E_n терпит разрыв, а нормальная составляющая вектора D_n непрерывна.

Граничные условия для касательных составляющих векторов D и E следуют из соотношения, описывающего циркуляцию вектора напряженности электрического поля. Построим вблизи границы раздела прямоугольный замкнутый контур длины l и высоты h (рис. 3.8).

Согласно теореме о циркуляции вектора Е электростатического поля

Обходя контур по часовой стрелке, представим циркуляцию вектора E в следующем виде:

(3.19)

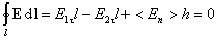
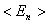
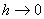
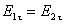
где — среднее значение E_n на боковых сторонах прямоугольника. Переходя к пределу при , получим для касательных составляющих E

. (3.20)

Для касательных составляющих вектора электрической индукции граничное условие имеет вид

(3.21)

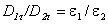
Таким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора E_τ непрерывна, а касательная составляющая вектора D_τ терпит разрыв.

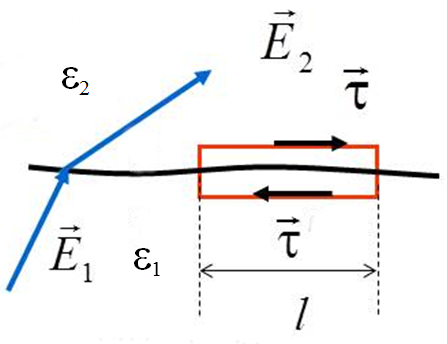
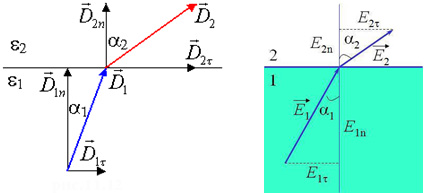
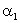
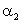
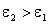
Преломление линий электрического поля. Из граничных условий для соответствующих составляющих векторов E и D следует, что при переходе через границу раздела двух диэлектрических сред линии этих векторов преломляются (рис. 3.9). Разложим векторы E₁ и E₂ у границы раздела на нормальные и тангенциальные составляющие и определим связь между углами и при условии . Легко убедиться, что как для напряженности поля, так и для индукции справедлив один и тот же закон преломления линий напряженности и линий смещения

Действительно, согласно рис.2.8 tgα₁/ tgα₂=D_1nD_2τ/D_1τD_2n. Воспользовавшись граничными условиями (3.17) и (3.21) придем к формуле (3.22). Аналогично можно убедиться в справедливости этой формулы и для вектора Е(рис. 2.9).

Из (3.22) следует, что при переходе в среду с большим значением ε угол α, образуемый линиями напряженности (смещения) с нормалью, увеличивается (рис.3.10).

Источник

Индукция (в физике)

D = E + 4p P

(4p ‒ постоянный коэффициент); в системе СИ

D = e 0 E + P,

В изотропном веществе, не обладающем сегнетоэлектрическими свойствами (см. Сегнетоэлектричество ), при слабых полях вектор поляризации прямо пропорционален напряжённости поля. В системе Гаусса

Подставляя выражение (3) в (1), получим:

D = (1 + 4pc е ) Е = e Е.

Р = c e e 0 E

Н = В ‒ 4p I,

В = Н + 4p I.

Намагниченность представляет собой магнитный момент единицы объёма и характеризует магнитное состояние вещества. В изотропной среде при слабых полях намагниченность прямо пропорциональна Н :

В = (1 + 4pc m ) H = m Н

В системе СИ эти формулы записываются следующим образом:

Лит.: Калашников С. Г., Электричество, М., 1970 (Общий курс физики, т. 2), гл. 5 и 11; Фриш С. Э. и Тиморева А. В., Курс общей физики, т. 2, М., 1953, гл. 15, 18.

Полезное

Смотреть что такое «Индукция (в физике)» в других словарях:

Индукция в физике — слово индукция употребляется в физике для обозначения явлений возбуждения в телах магнитного или электрического состояния, а также возникновения в них электрических токов под влиянием других тел, находящихся на расстоянии от первых и… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ИНДУКЦИЯ — ИНДУКЦИЯ, в физике, процесс электризации или намагничивания. В случае ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ электрический ток вызывается при помещении ПРОВОДНИКА в переменное МАГНИТНОЕ ПОЛЕ. Величина тока пропорциональна скорости изменения МАГНИТНОГО ПОТОКА … Научно-технический энциклопедический словарь

ИНДУКЦИЯ — (лат. inductio, от in в, и duco веду). 1) возбуждение электричества в проволоке посредством приближения её к электризованному телу. 2) метод мышления, иначе наз. наведение, при котором из частных положений выводят общее заключение. Словарь… … Словарь иностранных слов русского языка

Индукция — В Викисловаре есть статья «индукция» Индукция (из лат. inductio «выведение, наведен … Википедия

Индукция — (от лат. inductio наведение, выведение, возбуждение) 1) философский и вообще общенаучный метод движения знания от отдельного, особенного к всеобщему, закономерному; 2) логическое умозаключение от фактов к некоторой гипотезе (общему утверждению);… … Начала современного естествознания

Индукция — I ж. 1. Логическое умозаключение от частного к общему, от единичного наблюдения к обобщению, от фактов к некоторой гипотезе. Ant: дедукция 2. Способ математических доказательств и определений, основанный на переходе от утверждения, верного для… … Современный толковый словарь русского языка Ефремовой

Индукция — I ж. 1. Логическое умозаключение от частного к общему, от единичного наблюдения к обобщению, от фактов к некоторой гипотезе. Ant: дедукция 2. Способ математических доказательств и определений, основанный на переходе от утверждения, верного для… … Современный толковый словарь русского языка Ефремовой

Электростатическая индукция — Эксперимент с электроскопом показывающий возникновение индуцированного заряда … Википедия

Магнитная индукция — Не следует путать с явлением электромагнитной индукции. Магнитная индукция Размерность MT−2I−1 Единицы измерения СИ … Википедия

НЕПОЛНАЯ ИНДУКЦИЯ — (п р о б л е м а т и ч е с к а я, обобщающая, расширяющая и н д у к ц и я) – осн. вид индуктивных умозаключений. Важнейшая особенность Н. и. в том, что заключение в ней всегда содержит бóльшую информацию, чем посылки, именно поэтому ее нередко… … Философская энциклопедия

Источник

Что такое магнитная индукция

В этой статье мы постараемся разобраться в том, что такое магнитная индукция, как она связана с магнитным полем, какое отношение имеет магнитная индукция к току, и как действует на ток. Вспомним основные правила, определяющие направление индукционных линий, а также отметим некоторые формулы, которые помогут в решении задач магнитостатики.

Силовой характеристикой магнитного поля в выбранной точке пространства является магнитная индукция В. Эта векторная величина определяет силу, с которой магнитное поле действует на движущуюся в нем заряженную частицу. Если заряд частицы равен q, ее скорость равна v, а индукция магнитного поля в данной точке пространства равна В, то на частицу в данной точке со стороны магнитного поля действует сила, равная:

Таким образом, В — это вектор, величина и направление которого таковы, что сила Лоренца, действующая на движущийся заряд со стороны магнитного поля равна:

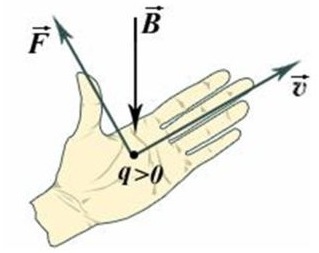
Здесь альфа — это угол между вектором скорости и вектором магнитной индукции. Вектор силы Лоренца F перпендикулярен вектору скорости и вектору магнитной индукции. Его направление для случая движения положительно заряженной частицы в однородном магнитном поле определяется правилом левой руки:

«Если левую руку расположить так, чтобы вектор магнитной индукции входил в ладонь, а четыре вытянутых пальца были направлены по направлению движения положительно заряженной частицы, то отогнутый на 90 градусов большой палец покажет направление силы Лоренца».

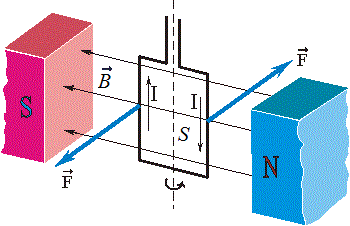
Поскольку ток в проводнике является движением заряженных частиц, то магнитную индукцию можно определить и как отношение максимального механического момента, действующего со стороны однородного магнитного поля на рамку с током, к произведению силы тока в рамке на площадь рамки:

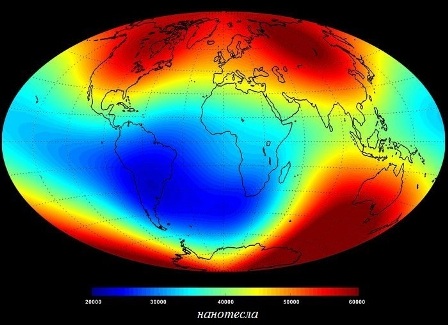
Кстати, индукция магнитного поля Земли на широте 50° в среднем составляет 0,00005 Тл, а на экваторе — 0,000031 Тл. Вектор магнитной индукции всегда направлен по касательной к магнитной силовой линии.

Сам термин индукция происходит от латинского «индукцио», что означает «наведение» (например, навести на мысль – то есть вызвать мысль). Синонимы: наведение, возникновение, образование. Не путать с явлением электромагнитной индукции.

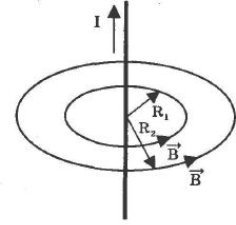
Проводник с током имеет вокруг себя магнитное поле. Открыл магнитное поле электрического тока в 1820 году датский физик Ханс Кристиан Эрстед. Для определения направления силовых линий индукции магнитного поля В электрического тока I, текущего по прямолинейному проводнику, пользуются правилом правого винта или буравчика:

«Направление вращения рукоятки буравчика показывает направление линий магнитной индукции В, а поступательное движение буравчика тогда соответствует направлению тока в проводнике.»

При этом величина магнитной индукции B на расстоянии R от проводника с током I может быть найдена про формуле

где магнитная постоянная:

Если линии напряженности электростатического поля Е начинаясь на положительных зарядах, заканчиваются на отрицательных, то линии магнитной индукции B замкнуты всегда. В отличие от электрических зарядов, магнитных зарядов, которые бы создавали полюса подобно электрическим зарядам, в природе не обнаружено.

Теперь несколько слов о постоянных магнитах. Еще в начале 19 века, французский исследователь и физик-естествоиспытатель Андре-Мари Ампер выдвинул гипотезу о молекулярных токах. Согласно Амперу, движения электронов вокруг атомных ядер порождают элементарные токи, которые в свою очередь создают вокруг себя элементарные магнитные поля. И если кусок ферромагнетика поместить во внешнее магнитное поле, то эти микроскопические магнитики сориентируются во внешнем поле, и кусок ферромагнетика станет магнитом.

Вещества с большим значением остаточной намагниченности, такие как сплав неодим-железо-бор, позволяют сегодня получать мощные постоянные магниты. Неодимовые магниты теряют не более 1-2 % своей намагниченности за 10 лет. Но их можно легко размагнитить, нагрев до температуры +70°C и более.

Надеемся, что данная статья помогла Вам получить общее представление о том, что такое магнитная индукция и откуда на возникает.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник