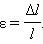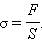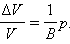Энергия деформации в чем измеряется

Энергия деформации в чем измеряется

Рассмотрим теперь общий случай определения потенциальной энергии деформации произвольно нагруженного упругого тела. Сначала будем считать, что на элемент тела действуют только нормальные напряжения (рис. 9.3). По граням элемента приложены напряжения . Изменения этих величин, вызванные приращением координат в пределах элемента, можно не учитывать, так как соблюдаются уравнения равновесия.

Работа внутренних сил упругости в результате деформации будет такой:

где .

Потенциальная энергия деформации равна

а удельная потенциальная энергия деформации —

В частном случае одпооспого растяжения получаются прежние зависимостн.

Перейдем к определению удельной потенциальной энергии при деформациях сдвига. На рис. 9.4 изображен элемент тела, испытывающий дефомацию сдвига в плоскости ху.

Рис. 9.3. Определение потенциальной энергии деформации при трехосном растяжении (сжатии)

Рис. 9.4. Определение на тенциальной энергии деформации при сдвиге

Первоначально прямой угол между осями х и у после деформации изменяется на величину

Работа внутренних сил упругости, характеризующихся касательными усилиями на гранях элемента, можег быть выражена таким образом:

Множитель 1/2, как и раньше, связан со статическим приложением усилий от нуля до максимальной величины к упругому телу. Вследствие свойства парности касательных напряжений

и с помощью соотношения (12) находим

Удельная потенциальная энергия, деформации при сдвиге в плоскости ху равна

Существенно, что удлинение ребер элемента не влияет на энергию: деформации сдвига, гак как касательные напряжения не производят работы при деформациях . Соотношения, подобные (13), справедливы при сдвиге в других плоскостях.

Объединяя результаты для растяжения и сдвига, получим общую формулу для удельной потенциальной энергии деформации:

В более кратком виде формулу (14) можно записать так:

где — векторы напряжений и деформаций; т — знак транспонирования.

Другие формулы, для удельной потенциальной энергии деформации получаются из основной зависимости (14) при учете соотношений упругости (разд. 18).

Если не принимать во внимание температурную деформацию, то для изотропного тела,

Внося соотношения (16) в формулы (14), получим после несложных преобразований

При выводе была учтена зависимость между модулем упругости Е и модулем сдвига

Формулу (17) можно записать в более кратком виде, если представить соотношения упругости в матричной форме (разд. 18):

Тогда получим следующий результат:

Последняя зависимость справедлива и для анизотропного тела, что отражается только в структуре матрицы.

Представим теперь удельную потенциальную энергию деформации как квадратичную функцию деформаций.

Для изотропного упругого тела, пренебрегая температурными деформациями, будем иметь (разд. 18)

где — средняя деформация.

Из соотношения (14) получаем

или в другой форме

Дадим матричную запись уравнений (21) и (22). Так как

где — матрица коэффициентов жесткости, то из соотношения (15) получаем

Последнее равенство справедливо и для анизотропного тела, если соответствующим образом выбрать матрицу коэффициентов жесткости.

Отметим еще две группы соотношений, представляющие интерес в теоретическом плане. Они получаются непосредственным дифференцированием равенств (17) и (22):

Источник

Энергия деформации в чем измеряется

В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания (см. §3.1). Силы взаимодействия между частицами обусловливают механические свойства твердых тел.

Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.

Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 3.7.1.

Отношение абсолютного удлинения к первоначальной длине образца называется относительным удлинением или относительной деформацией :

Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то при деформации растяжения и – при сжатии. Отношение модуля внешней силы к площади сечения тела называется механическим напряжением :

За единицу механического напряжения в СИ принят паскаль (). Механическое напряжение измеряется в единицах давления.

Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).

На рис. 3.7.1 (3) показана деформация всестороннего сжатия твердого тела, погруженного в жидкость. В этом случае механическое напряжение совпадает с давлением в жидкости. Относительная деформация определяется как отношение изменения объема к первоначальному объему тела. При малых деформациях

Величина модуля всестороннего сжатия определяет скорость звука в данном веществе (см. §2.7).

Источник

Энергия деформации в чем измеряется

Постановка задачи.

Кроме рассмотренных способов вычисления прогибов и углов поворота сечений балок существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.

При статическом растяжении или сжатии упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза полностью переходит в потенциальную энергию деформации стержня. Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится.

Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.

Мы условились называть «статической» такую нагрузку, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения, этих частей, т. е. их скорость остается постоянной и ускорение отсутствует.

При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой. При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере.

Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу. Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.

Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы. Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.

Обозначим величину накопленной потенциальной энергии деформации через U, а уменьшение потенциальной энергии внешних нагрузок . Тогда величина измеряется положительной работой этих нагрузок , с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, междучастичных сил А, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.

Закон сохранения энергии при деформациях упругих систем принимает вид:

заменяя в этой формуле величины и U численно равными им значениями работ и —А, получаем иную формулировку этого закона:

или

Эта формулировка закона сохранения энергии совпадает с так зазываемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю.

Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии.

Таким образом, потенциальная энергия деформации численно равна работе внешних сил , проделанной ими этой деформации:

Вычисление потенциальной энергии.

При вычислении потенциальной энергии будем предполагать, что деформации не только материала, но и всей конструкции, следуя закону Гука, пропорциональны нагрузкам, т. е. линейно с ними связаны и растут постепенно вместе с ними.

Известно, что при статическом растяжении или сжатии стержня силами Р величина работы , а следовательно, и величина энергии U равняется:

Так же как и при кручении, может быть вычислена потенциальная энергия при чистом изгибе.

Концевые сечения балки под действием изгибающих моментов(Рис.1) повернутся на угол , где — центральный угол изогнувшейся по дуге радиусом р оси балки.

Рис.1. Модель расчета потенциальной энергии при чистом изгибе.

так как из общей теории изгиба а

Из полученных выражений следует, что потенциальная энергия деформации равна половине произведения силы или пары сил на перемещение по ее направлению того сечения, где эта сила приложена. Условимся называть термином «обобщенная сила» всякую нагрузку, вызывающую соответствующее нагрузке перемещение, т. е. и сосредоточенную силу, и пару сил, и т. п.; перемещение же, соответствующее этой силе, будем называть «обобщенной координатой».

«Соответствие» заключается в том, что речь идет о перемещении того сечения, где приложена рассматриваемая сила, причем о таком перемещении, что произведение его на эту силу дает нам величину работы; для сосредоточенной силы это будет линейное перемещение по направлению действия силы — прогиб, удлинение; для пары сил — это угол поворота сечения по направлению действия пары.

Иначе: потенциальная энергия деформации численно равна половине произведения обобщенной силы на соответствующую ей координату.

,

где Р—обобщенная сила, — обобщенная координата.

Полученные соотношения также показывают, что потенциальная энергия является функцией второй степени от независимых внешних сил, так как в эти формулы не входят реакции, зависящие от приложенных к элементу сил и связанные с ними уравнениями равновесия. Из тех же формул видно, что величина потенциальной энергии деформации является функцией второй степени от «обобщенных координат» системы и вполне ими определяется. Таким образом, порядок приложения нагрузок в этом отношении безразличен, важна лишь окончательная форма деформированного элемента. Поэтому, хотя результаты этого параграфа получены в предположении, что нагрузка возрастает статически, при сохранении равновесия в течение всего процесса нагружения, однако выведенные формулы сохраняют силу и при любом способе приложения нагрузок, лишь бы значения сил и деформаций были связаны линейной зависимостью и относились к тому моменту, когда установится равновесие конструкции.

Известно также, что в общем случае изгиба изгибающий момент М(х) является величиной переменной. В любом сечении ему будет сопутствовать поперечная сила Q(х). Поэтому рассматривать следует уже,не всю балку в целом, а лишь бесконечно малый элемент балки длиной dx.

Рис.2. Энергетическая модель поперечного изгиба

Под действием изгибающих усилий сечения элемента (рис.2, а) поворачиваются и образуют между собой угол (Рис.2, б). Касательные же усилия стремятся вызвать (Рис.2, в) перекос элемента; таким образом перемещения от нормальных напряжений идут перпендикулярно к направлению касательных напряжений, и наоборот.

Это позволяет независимо вычислять работу изгибающих и касательных усилий.

Обычно работа касательных усилий оказывается малой по сравнению с работой нормальных, поэтому мы пока ею будем пренебрегать. Элементарная работа нормальных усилий (как и в случае чистого изгиба) равна:

Рис.3. Расчетная схема примера расчета потенциальной энергии при поперечном изгибе.

Вся потенциальная энергия изгиба получится суммированием по длине балки

Знак предела интегрирования условно указывает, что интегрирование должно охватить всю балку; в тех случаях, когда для М(х) мы имеем несколько участков, то интеграл приходится разбивать на сумму интегралов.

Вычислим потенциальную энергию балки на двух опорах, нагруженной силой Р (Рис.3). Эпюра моментов имеет два участка; поэтому

Источник

Лекционный материал по теме №5

Описание

В лекции рассматриваются следующие темы:

Упругие параметры физических тел. Понятия о напряжениях и деформациях. Объемные деформации горных пород. Модуль сжатия и модуль сдвига. Модуль Юнга и коэффициент Пуассона. Коэффициенты Ламе. Закон Гука. Способы и единицы измерения упругих модулей горных пород (статические и динамические методы). Динамические характеристики упругих сред. Анизотропия параметров упругости. Скорости упругих волн и упругие модули химических элементов и минералов. Скорости упругих волн в магматических и метаморфических породах. Скорости упругих волн в пористых осадочных породах. Модели распространения упругих волн в осадочных породах. Зависимость скоростей от давления и температуры. Модели многофазных сред поглощения упругих волн.

Оглавление

1. Упругие параметры физических тел

Упругость – свойство вещества оказывать влияющей на него силе механическое сопротивление и принимать после её спада исходную форму. Противоположность упругости называется пластичность.

Упругость тел – одна из основных физических констант, связанная с внутренним строением вещества.

Упругость характеризует свойство веществ сопротивляться изменению их объема и формы (твердые тела) или только объема (жидкости, газы) под воздействием механических напряжений, что обуславливается возрастанием внутренней энергии веществ.

При упругих деформациях вещество восстанавливает свои первоначальные объем и форму после прекращения действия сил, вызывающих их деформацию. В простейших случаях малых деформаций зависимость линейная – и действует закон Гука, на котором основана теория упругости. Согласно этой теории малые деформации пропорциональны приложенной нагрузке:

(5.1, 5.2 )

где Δl/l и Δd/d –относительная продольная и поперечная деформация; F— приложенная к телу нагрузка в кг, S – площадь поперечного сечения тела в м 2 ; F/S – напряжение.

1.1. Модуль Юнга и коэффициент Пуасона

Количественными характеристиками упругих свойств являются модули упругости.

1) модуль Юнга E (модуль продольной упругости) – это отношение нормального напряжения к относительному удлинению, вызванному этим напряжением в направлении его действия. Модуль Юнга характеризует способность тел сопротивляться деформации растяжения или сжатия:

(5.3)

2) коэффициент Пуассона σ_П (коэффициент поперечного сжатия) – отношение поперечного сжатия тела при одноосном растяжении к продольному удлинению. Коэффициент Пуассона равен абсолютному значению отношения относительной поперечной деформации тела к относительной продольной деформации:

(5.4, 5.5)

В твердых породах коэффициент Пуассона изменяется от 0,1- до 0,4. Чем больше значение коэффициента Пуассона, тем больше порода может деформироваться. Более однородные по минеральному составу породы характеризуются более низкими значениями коэффициента Пуассона.

1.2. константа Ламе и модуль сдвига

(5.6)

где K модуль объемного сжатия.

4 ) модуль сдвига G. Модуль сдвига определяет способность тел сопротивляться изменению формы при сохранении их объема:

, (5.7)

где r – касательное напряжение; α – угол сдвига.

Модуль сдвига численно равен другой константе Ламе:

(5.8)

1.3. Скорости упругих волн

В телах под действием механических напряжений возникают деформации и генерируются разные по природе упругие колебания (волны) продольные p и поперечные s. Продольные волны являются результатом деформации типа сжатия – растяжения, поперечные – сдвига. В свободных газах и жидкостях возникают только продольные волны и отсутствуют поперечные.

Скорость упругих волн равна отношению длины пути соответствующей волны к времени пробега этого пути:

(5.9, 5.10)

Для геофизиков большое значение имеют скорости, которые связаны с модулями упругости и плотностью.

Скорость продольных упругих волн или упругих колебаний, возникающих вследствие деформаций растяжение-сжатие в любой среде:

(5.11)

Скорость поперечных волн или упругих колебаний, возникающих вследствие деформаций сдвига в твердой среде:

(5.12)

Скорости v_p и v_s в принципе независимые величины. Связь между ними осуществляется через коэффициент Пуассона:

(5.13)

При сейсморазведочных работах вычисляют ряд скоростных параметров разреза: граничную, пластовую, среднюю, эффективную и лучевую скорости.

2. Динамические характеристики упругих сред

Распространение упругих колебаний сопровождается затуханием их амплитуды по мере удаления от источника. Амплитуда A гармонической волны с частотой w убывает с расстоянием l в однородной поглощающей среде по закону:

, (5.14)

3. Скорости уругих волн и упругие характеристики химических элементов и минералов

По упругим характеристикам химические элементы весьма неоднородны. В упругой характеристике элементов играют роль их электронная оболочка, которая является упругой средой, и ядра атомов, обладающие различной массой. Упругие модули в элементах изменяются в зависимости от величины атомного радиуса элемента и его атомной массы.

Значения E, G, K, n получены для важнейших породообразующих минералов осадочных, магматических и метаморфических пород, а также для рудных минералов и чистых самородных металлов.

По модулям E, G и K минералы подразделяются на четыре группы:

Данные о скорости распространения продольных упругих волн в элементах были получены экспериментально или рассчитаны по модулям упругости.

Наблюдается корреляция с плотностью и атомными радиусами в пределах периода. Скорость увеличивается в элементах первой половины каждого периода и уменьшается в элементах второй половины каждого периода. Наибольшая зависимость скорости от атомного радиуса установлена у sp—элементов с большим размерами атомов. Зависимость скорости у sp-элементов от атомной массы – незначительна. Для d—элементов скорость в основном определяется атомной массой вещества. Скорость уменьшается при увеличении массы вещества. Это справедливо и для скоростей продольных волн и для скоростей поперечных волн. Поскольку они связаны соотношением .

Упругие свойства минералов определяются характеристиками их внутреннего строения. Наиболее информативной характеристикой является плотность упаковки атомов ω в единице объема вещества. Параметр ω обратно пропорционален атомному радиусу. Чем больше плотность упаковки, тем меньше атомный радиус. Значение параметра вычисляется по формуле (Н.З.Евзикова, Ю.В.Казицин, В.А. Рудник):

. (5.15)

Скорость упругих волн увеличивается с ростом плотности упаковки и уменьшается с ростом средней атомной массы, являющейся мерой инерционности вещества.

Скорость продольных волн в минералах изменяется от 2000 до 18000 м/с, поперечных от 1100 до 10000 м/с. Низкие скорости характерны для самородных металлов (золото, платина), высокие – для алюмосиликатных и окисных безжелезистых минералов (топаз, шпинель, корунд), наибольшая скорость упругих волн установлена в алмазе.

Характер изменения скорости упругих волн в элементах, минералах и горных породах имеет два типа связи между скоростью продольных волн и плотностью твердых образований:

; .

Уравнение связи между σ и v_P в образованиях первого типа имеет вид:

, (5.16)

Ко второму типу относятся тяжелые металлы, сульфиды, окисные рудные минералы и самородные металлы, состоящие преимущественно из элементов со структурой типа d. В этих элементах и минералах существенное слияние на физические параметры оказывает атомная масса. Модуль Юнга и модуль сдвига, скорость упругих волн уменьшается с ростом плотности. В минералах второго типа наблюдается некоторое уменьшение плотности упаковки атомов в веществе и значительное увеличение их средней атомной массы (от 20 до 200 а.е.м).

Таким образом, наиболее информативными характеристиками для определения упругих свойств элементов являются плотность упаковки и атомная масса. В общем виде зависимость скорости упругих волн может быть представлена выражением:

(5.17).

4. Скорости упругих волн в магматических и метаморфических породах

Упругие характеристики магматических и метаморфических пород определяются в значительной мере:

Основными химическими компонентами горных пород являются окислы кремния, калия, натрия, алюминия, кальция, магния и железа. Наименьшей скоростью упругих волн характеризуются породы, обогащение такими легкими окислами, как окислы кремния, калия, натрия. С уменьшением их содержания в породах возрастает содержание окислов кальция, магния, железа. Для ассоциаций горных пород, сложенных малоупругими минералами кислого состава (кварц, калиевой полевой шпат, альбит, олигоклаз) характерны минимальные скорости упругих волн. Максимальными скоростями обладают горные породы, представленные высокоупругими минералами основного состава (лабрадор, амфибол, пироксен, оливин). Таким образом, скорость упругих волн увеличивается с увеличением основности. То есть в ряду гранит-габбро-перидотит наблюдается возрастание средней скорости продольных и поперечных волн с ростом основности.

Однако следует заметить, что на упругие свойства горных пород воздействует множество факторов и не существует однозначной связи между геологическим определением породы и ее скоростной характеристикой. Породы сложенные одними и теми же минеральными ассоциациями могут отличаться по своим скоростям, так же как и совершенно разные породы могут иметь одинаковые значения скоростей. Поэтому обычно указываются пределы вероятных скоростей.

Наиболее часто встречающиеся в магматических породах величины V_P и V_S составляют соответственно:

гранитоиды 5,4-6,1 км/с и 2,9-3,5 км/с;

диориты 6,1-6,2 и 3,4-3,7 км/с;

анортозиты и габброиды 6-7,2 км/с и 3,5-4,1 км/с;

гипербазиты 7,4-8,2 км/с и 4-4,6 км/с.

То же наблюдается и в метаморфических породах:

гнейсы 5,6-5,9 км/с и 2,7-3,7км/с;

амфиболиты 6,2-6,8 км/с и 3,6-4 км/с;

гранулиты среднего и основного состава 6,2-6,8 км/с,

эклогиты 7,2-7,8 км/с и 4,1-4,4 км/с.

Для эффузивных пород характерен широкий диапазон значений скоростей, обусловленный различной пористостью, первоначальной структуры пород и их последующим диагенезом.

Для метаморфических пород в целом также наблюдается зависимость скорости упругих волн от минерального состава основности пород. При региональном метаморфизме скорость упругих волн возрастает от низших стадий метаморфизма к высшим за счет уплотнения пород. Причем, в кислых породах скорость упругих колебаний увеличивается на 3-5%, у пород основного состава возрастание скорости может достигать 15-25 %.

Автометаморфизм приводит к снижению скорости упругих колебаний. Процесс серпентинизации сопровождается разложением высокоупругого оливина с образованием структурно-рыхлого серпентина. Скорость снижается с 8,2 км/с до 5,5 км/с. При амфиболизации габбро-норитов и гипербазитов образуется амфиболы плагиоклазы, структурно-рыхлые хлориты, серициты, эпидоты, что также уменьшает скорость продольных волн. В неизмененных гипербазитах скорость продольных волн достигает 8,2 км/с. Скорость амфиболизированных гипербазитов равна 7,6км/с.

Процессы ультраметаморфизма приводят к уменьшению скорости упругих волн. Величина скорости продольных волн при чарнокитизации и гранитизации уменьшается до 5,5-6 км/с.

Существенное влияние на скоростные характеристики оказывают гипергенные процессы, приводящие к росту трещиноватости и образованию структурно-рыхлых минералов. Породы кислого состава в большей степени подвержены процессам выветривания. Уменьшение скорости упругих волн может при этом достигать 200-300%.

Анизотропия упругих свойств магматических и метаморфических пород обусловлена закономерных расположением порового пространства и минеральных зерен, а также кристаллической решеткой минералов. Значения скорости распространения продольных волн вдоль слоистости выше, чем измеренные перпендикулярно направлению слоистости. Коэффициент анизотропии для продольных волн достигает значений 1,2-1,3 и обычно превышает значение анизотропии для поперечных волн. Изверженные породы с массивной структурой характеризуются слабой анизотропией. Значение коэффициента анизотропии составляет 1,0-1,06. Наибольшие значения коэффициентов анизотропии наблюдаются в метаморфических породах, обладающих гнейсовидной и сланцевой текстурой. В частности биотитовые и биотит-амфиболовые гнейсы характеризуются значениями коэффициентов анизотропии 1,02-1,19, а высокоглиноземные гнейсы 1,04-1,23.

Скорости продольных волн в уплотненных осадочных породах (метаморфизованные песчаники, кристаллические известняки, доломиты) практически не отличается от скорости продольных волн, измеренных в магматических и метаморфических породах при одной и той же плотности.

5. Скорости упругих волн в осадочных породах

Упругие свойства осадочных пород определяются составом, пористостью, диагенезом пород и свойствами порового заполнителя. В общем случае скорость продольных волн в осадочных породах изменяется от 0,3 до 6,9 км/с. Отношение v_P/v_S различна у различных пород: в глине 0,07-0,6, в лессе 0,3-0,6, в песке 0,1-0,3. Модуль Юнга изменяется от 3 ГПа в глине до 165 ГПа в доломите. Коэффициент Пуассона изменяется в пределах 0,1-0,45.

Максимальные скорости упругих волн и модулей упругости отмечаются в уплотненных карбонатных породах, меньше величины этих параметров наблюдаются в уплотненных песчано-глинистых и гидрохимических образованиях. Зависимость между v_P и σ для осадочных пород выведена М.Л.Озерской (1965):

, (5.18)

По предложенному выражению составлены палетки со значениями v_Pmin, v_Pmax, σ_max.

При пористости 1-2% скорости упругих волн в осадочных породах близки к скоростям в магматических и метаморфических породах кислого состава. В ряде случаев скорости упругих волн в доломитах сравнима со скоростями в габброидах.

Существует ряд теоретических и экспериментальных зависимостей, позволяющих оценить влияние пористости, трещиноватости, типа заполнителя пустот в породах на скорость продольных волн. Широко применяется уравнение «среднего времени», связывающего время распространения волны в объеме распространения волны в заполнителе порового пространства и минеральном скелете:

, (5.19)

Осадочные породы – преимущественно анизотропные среды. Анизотропия скоростей упругих волн обуславливается слоистостью и направлением трещиноватости пород. Особенно ярко выражено явление анизотропии для образований с тонким переслаиванием в них глинистых пород. Коэффициент анизотропии продольных волн в этих случаях может достигать 1,2-1,3.

Фактором, влияющим на скорость упругих волн в осадочных породах, является тип заполняющего породу флюида. Насыщение порового пространства среды жидкостью, химически не взаимодействующей с минеральным скелетов породы, обуславливает увеличение скорости упругих волн. При насыщении песчаников и алевролитов раствором соли NaCl не приводящим к большому эффекту размокания присутствующих в породе глинистых минералов, скорость продольных волн увеличивается с 5-10 до 100 –120%. Влияние насыщающей жидкости на скорость связано с пористостью породы, то количественно эффект насыщения пропорционален коэффициенту пористости породы.

Насыщение глин и глинистых песчаников водой приводит к разбуханию глинистых минералов, потере связанности породы и уменьшение скорости.

Резкое возрастание сейсмических скоростей в породе вызывает замерзание воды, находящиеся в порах, кавернах, трещинах. Так как скорость продольных волн во льду почти в 2,5 раза выше, чем в воде. Поэтому скорость может возрастать на 1- 2 км/с.

Скорость увеличивается с возрастом пород, глубиной залегания, степенью цементации. Увеличение скорости с глубиной происходит из-за роста горного давления. Поскольку уменьшается пористость пород, увеличивается модуль Юнга и, соответственно, увеличивается скорость продольных волн. Это явление наиболее выражено для терригенных пород, которые отличаются высокой начальной скоростью. В карбонатных отложениях это свойство проявляется слабо, и практически не заметно для хемогенных осадков.

Переход осадочных пород из газонасыщенного в водонасыщенное состояние сопровождается изменением упругих модулей. Модуль Юнга в низкопористых образцах увеличивается до 100-120%. Модуль сдвига может как увеличиваться (на 20-30%), так и уменьшаться (до 20%).

Экспериментально установлен рост процесса поглощения α с увеличением пористости пород. Установлен рост значений α_P и α_S с увеличением глинистости осадочных образований.

Большое значение имеют термодинамические условия залегания нефти и газа. С повышением температуры скорость распространения упругих волн уменьшается, причем наиболее ярко в нефтенасыщенных породах (до 30%) по сравнению с газо- и водонасыщенными. Увеличение давления (глубины), наоборот, ведет к повышению скорости.

6. Методы изучения упругих свойств

Методы измерения упругих свойств можно подразделить на две большие группы, относимые к измерениям в естественном залегании и в лабораторных условиях.

Упругие модули горных пород измеряются двумя методами: статическим (изотермические) и динамическим (адиабатические модули).

Статический метод применяется для определения:

Статистические способы определения статических деформаций основываются на наблюдениях ориентированных кристаллических образцов. Для этого используют крупные образцы в виде стержней или пластин. Длина стержня должна быть значительно больше, чем размеры поперечного сечения. Полученные величины деформаций используют для расчета значений упругих параметров вещества.

Во всех случаях измерение упругих параметров сводится к непосредственному измерению деформации сжимаемых образцов тензометрами различной конструкции.

С помощью динамического метода измеряют различные виды упругих волн в веществе и их затухание. Различают:

Для определения упругой характеристики горных пород в естественном залегании применяют вертикальное сейсмическое профилирование (ВСП), сейсмический каротаж (СК), акустический каротаж и полевые сейсмические методы. Ценные сведения о скоростных характеристиках дают сейсмические исследования методом преломленных и отраженных волн, особенно в районах, где общие черты геологического строения достаточно хорошо известны.

Источник