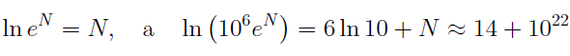Энтропия стремится к чему
Просто о сложном
Энтропия. Как часто можно услышать или прочитать это красивое, умное слово. Но какой смысл оно несет в себе?
В современном же варианте она определяется как логарифм числа состояний, в которых может находиться система. Рассмотрим одну интересную особенность энтропии:
В одном кубическом метре воздуха находится
Как видите, ошибка студента в целый миллион раз никак не повлияла на определенную им энтропию системы. Вот, какое оно огромное, это число.
Пытливый ум читателя задастся вопросом: как студенту может пригодиться определенная им энтропия? Дело в том, что при равновесном состоянии система имеет наибольшее количество допустимых состояний, а значит, и наибольшую энтропию. Энтропия системы, на которую не действуют внешние факторы, всегда либо растет, либо остается постоянной, если она (система) достигла состояния равновесия. Это закон природы, который выполняется всегда, так же, как и всегда тепло передается от более горячего тела к более холодному. Существует вероятность, что тепло уйдет от холодного к горячему, но она настолько ничтожна, что это событие не произойдет никогда за все время существования нашей вселенной.
Так что же это получается, по отношению к нашему миру второй закон термодинамики не работает? Как могли образоваться сложнейшие формы жизни, что это, если не признак порядка? Согласно теории эволюции Дарвина, в основе процесса естественного отбора лежит повышение степени организованности биологических систем. Вид все более и более совершенствуется в процессе эволюции. Мы не видим в природе хаотической смеси различных атомов, расположенных вперемешку друг с другом, что соответствовало бы большему беспорядку в системе. Наоборот, мир сильно структурирован. Почему-то растут деревья, в небе плавают облака, летают какие-то бабочки. В море зачем-то плавают рыбы. Как же можно объяснить возникновение структур в открытых системах?
Все объясняется довольно просто. Рассмотрим замкнутую систему, состоящую из нескольких подсистем. Сумма их энтропий возрастает в четком соответствии со вторым законом термодинамики, но энтропия одной из подсистем при этом может убывать, не нарушая при этом никаких законов физики, а это значит, что в ней может возникать порядок.
Ставлю тег «моё», но много информации брал из лекций нашего физика, если понравится, следующий пост будет о чем-то наподобие тепловой смерти вселенной, пока не придумал.
Все меняется, и некоторым из нас это не всегда нравится. Но согласно одной из точек зрения, энтропия Вселенной и природы в целом (то есть степень беспорядка или случайности в системе) может быть тем, что в первую очередь способствовало возникновению жизни.
реклама
Согласно этой точке зрения, когда группа атомов приводится в движение внешним источником энергии, например Солнцем, и окружена источником тепла, например атмосферой, она постепенно перестраивается таким образом, чтобы рассеивать все больше энергии. С этого момента, при определенных условиях, материя неумолимо приобретает свойства, ассоциирующиеся с жизнью.
Однако энтропию также связывают с тепловой смертью Вселенной. Вот все, что необходимо знать об энтропии в термодинамике и о том, как она влияет на Вселенную и, в конечном счете, на нас.
Что такое энтропия Вселенной?
Хотя в физике это не одно и то же, полезно вспомнить о теории хаоса и о том, как она связана с энтропией, и, в конечном счете, какое влияние энтропия может оказывать на Вселенную.
реклама
Согласно теории хаоса, в кажущейся случайности хаотических, сложных систем есть скрытые закономерности и взаимосвязи. Если знать начальные условия и выяснить эти базовые закономерности, то можно предсказать нарушения, которые произойдут в будущем. Другими словами, хаос не так беспорядочен и случаен, как может показаться.
В своей самой простой формулировке энтропия определяется как мера тепловой энергии в системе на единицу температуры, которая не может быть использована для совершения полезной работы. Поскольку работа получается в результате упорядоченного движения молекул, энтропия также является мерой молекулярного беспорядка, или случайности, в системе.
Не только физика, но и многие дисциплины нашли применение этой концепции, включая химию, биологию, изменение климата, социологию, экономику, теорию информации и даже бизнес.
Но давайте остановимся на физике, а точнее, на фундаментальных законах термодинамики.
Кто ввел понятие энтропии?
реклама
Несмотря на то, что понятие энтропии применяется в различных дисциплинах, оно берет свое начало в физике. Изучая сохранение механической энергии в своей работе » Основные принципы равновесия и движения» (1803), французский математик Лазар Карно предложил, что ускорения и удары движущихся частей в машине представляют собой «потери момента активности». Момент активности» Карно сопоставим с современным понятием работы в термодинамике. Таким образом, в любом естественном процессе существует неотъемлемая тенденция к рассеиванию полезной энергии.
Другие ученые исследовали эту «потерянную» энергию, и в последней половине 19 века они указали, что это не настоящее исчезновение, а преобразование. Это и есть концепция сохранения энергии, которая проложила путь к первому закону термодинамики. Такие ученые, как Джеймс Джоуль, Юлиус Майер, Герман Гельмгольц и Уильям Томпсон (также известный как лорд Кельвин), опубликовали работы, исследующие эту концепцию.
реклама
Но термин «энтропия» появился в работах немецкого физика Рудольфа Клаузиуса, который сегодня считается одним из авторов термодинамики.
В 1850-х годах он представил изложение Второго закона термодинамики применительно к тепловому насосу. Заявление Клаузиуса подчеркивало тот факт, что невозможно построить устройство, работающее по циклу и не производящее никакого другого эффекта, кроме передачи тепла от более холодного тела к более горячему.
В 1860-х годах он придумал слово «энтропия» от греческого слова, означающего превращение, или поворотный пункт, для обозначения необратимой потери тепла. Он описал ее как функцию состояния в термодинамическом цикле, в частности в цикле Карно, теоретическом цикле, предложенном сыном Лазаря Карно, Сади Карно.
В 1870-х годах австрийский физик и философ Людвиг Больцман переосмыслил и адаптировал определение энтропии к статистической механике. Ближе к тому, что подразумевает этот термин сейчас, он описывает энтропию как измерение всех возможных микро-состояний в системе, макроскопическое состояние которой было изучено. Как могут измениться все наблюдаемые свойства системы? Сколькими способами? Эти вопросы охватывают понятие беспорядка, которое лежит в основе одного из понятий энтропии.
Находится ли Вселенная в состоянии энтропии?
Еще в 19 веке Рудолф Клаузиус вывел, что энергия Вселенной постоянна, а ее энтропия имеет тенденцию к увеличению с течением времени.
По мнению космологов, затем эта точка «взорвалась», расширяясь и распространяясь со скоростью, превышающей скорость света, и породив все частицы, античастицы и излучения во Вселенной.
Конечно, для этого должно было произойти огромное количество процессов связанных с изменением энтропии. Однако если мы подумаем о непрерывном увеличении энтропии, которое происходило на протяжении всех этих лет, то сможем сделать вывод, что энтропия Вселенной сейчас должна быть намного больше. На самом деле, согласно расчетам, энтропия Вселенной сегодня примерно в квадриллион раз больше, чем во время Большого взрыва.
Почему энтропия Вселенной растет?
Черные дыры обладают огромной концентрацией массы, которая обеспечивает им исключительно сильное гравитационное поле. Поэтому они допускают множественность микросостояний. В связи с этим Стивен Хокинг предположил, что черные дыры выделяют тепловое излучение вблизи своих горизонтов событий. Это излучение Хокинга может привести к потере массы и окончательному испарению черных дыр.
Но помните, что черные дыры подчиняются второму закону термодинамики, который гласит, что энтропия всегда будет иметь тенденцию к увеличению. Поэтому они будут набирать все большую массу и сливаться с другими черными дырами, превращаясь в сверхмассивные чёрные дыры. А когда они в конце концов распадутся, излучение Хокинга, создаваемое распадающимися чёрными дырами, будет иметь такое же количество возможных состояний, как и сама ранее существовавшая черная дыра. Согласно этой точке зрения, ранняя Вселенная имела низкую энтропию из-за меньшего количества или гораздо меньших размеров черных дыр.
Существует ли предел энтропии во Вселенной?
Как бы мы ни говорили о тенденции к увеличению энтропии, законы термодинамики также подразумевают состояние максимальной энтропии.
В повседневной жизни мы можем наблюдать это, когда наш кофе остывает в чашке. Когда кофе достигает комнатной температуры, это означает, что он находится в тепловом равновесии с окружающей средой. В кипящей воде, используемой для приготовления кофе, было много возбужденных атомов, но они замедлились и в конце концов достигли максимальной энтропии для данной системы.
При постоянной, стабильной температуре во всем космосе больше не останется энергии для совершения работы, так как энтропия достигнет максимального уровня. Все эти предположения составляют теорию тепловой смерти Вселенной. Эта теория также известна под названием «Большой заморозки», поскольку в этом сценарии энтропия Вселенной будет постоянно возрастать, пока не достигнет максимального значения. В этот роковой момент все тепло в нашей Вселенной будет распределено абсолютно равномерно, не оставляя места для полезной энергии.
Может ли энтропия Вселенной уменьшиться?
Можно с уверенностью сказать, что энтропия во Вселенной в какой-то момент уменьшилась, потому что в ней существует определенный порядок. Гравитационные взаимодействия могут к примеру превращать туманности в звезды. Это своего рода порядок.
Энтропия может уменьшаться без нарушения второго закона термодинамики до тех пор, пока она увеличивается в других частях системы. В конце концов, второй закон термодинамики не говорит, что энтропия не может уменьшаться в определенных частях системы, а только то, что общая энтропия системы имеет естественную тенденцию к увеличению.
При этом общая энтропия Вселенной не уменьшается. Как было сказано выше, энтропия будет иметь тенденцию к увеличению, пока не достигнет своего максимального уровня и не приведет к тепловой смерти. Это стационарное состояние термодинамического равновесия, в котором энтропия не только максимальна, но и постоянна, и она будет оставаться такой, пока не произойдет приток энергии, который оживит систему.
Тогда цикл может повториться. С новой, дополнительной энергией, совершающей работу, останется часть энергии, не способной совершить работу, которая превратится в тепло. Это снова увеличит энтропию системы. Но откуда возьмется эта энергия? Что заставит оставшиеся лептоны и фотоны, если таковые имеются, взаимодействовать?
Просто о сложном: почему все вокруг стремится к хаосу и как это остановить
Теории и практики
Когда порой вы чувствуете нарастающий уровень энтропии, но не понимаете почему, ответ кроется в физике: стремление мира к хаосу — фундаментальное свойство природы. Из чего состоит хаос, обратим ли он, можно ли его как-то измерить и почему существует выражение «ломать — не строить»? Обо всем этом T&P рассказал научный журналист, сотрудник кафедры физики и астрофизики МФТИ Айк Акопян в рамках проекта «Физтех.Читалка».
Что происходит, когда мы приводим в движение маятник? Он начинает колебаться, каждый раз уменьшая амплитуду. Через некоторое время мы обнаружим, что маятник остановился. Но куда делась энергия маятника? Те, кто в школе на уроках физики слушал учителя внимательно, ответят, что энергию заберут молекулы воздуха. Но почему не происходит обратное? Почему молекулы вдруг не могут собраться и, наоборот, передать энергию маятнику?
Дело в том, что стремление мира к хаосу оказывается фундаментальным свойством природы. Направленное движение частиц маятника превращается в хаотичное движение молекул воздуха. Направленное течение воды рано или поздно превратится в хаотичную струю с турбулентными вихрями и извивающимися, переплетающимися друг с другом потоками.
Наша природа вовсю стремится к хаосу, но неужели это стремление бесконечно? В какой момент система достигает какого-то спокойствия? В какой момент это стремление прекращается? В XIX веке Максвелл и ряд других физиков показали, что, если оставить систему в покое, она действительно придет к определенному состоянию «спокойствия». Это состояние называется равновесным, и, чтобы его понять, нужно забыть об индивидуальной скорости, координате каждой частицы и взглянуть на коллективные характеристики системы. Например, на то, сколько частиц на данный момент имеют определенные скорости.
Если мы построим график числа частиц от скорости, то увидим удивительную вещь: система из любого состояния, каким бы это состояние ни было изначально, в итоге приходит к одному определенному распределению числа частиц от скорости, которое называется распределением Максвелла. Это состояние является конечным пунктом назначения любой системы, и в ней достигается максимальный хаос.
Но… Как вообще измерить хаос? В физике для измерения хаоса используют величину, которая называется энтропией системы. Чем больше энтропия, тем менее упорядочена система. В состоянии равновесия энтропия максимальна. Больцманом в XIX веке была доказана так называемая H-теорема, которая гласит, что в замкнутой системе энтропия со временем всегда возрастает.
Не совсем. Представьте, что у вас есть замкнутая комната с кучей шариков, которые летят и врезаются друг в друга. Все абсолютно идеально, столкновения упругие, никаких потерь энергии. Через достаточное количество времени распределение скоростей будет в точности максвелловским, энтропия необратимо возрастет до максимума.
Данные телескопа Planck показали, что примерно 98% энергии нашей Вселенной не заключено в звездах и вообще в обычном веществе, из которого состоим мы
Но давайте взглянем на каждый шарик по отдельности. Дело в том, что для каждого шарика мы можем узнать в точности его скорость и координату, а также действующую на него силу. Из второго закона Ньютона можем узнать ускорение — и все: движение каждой отдельной частички можно совершенно однозначно задать. Закон Ньютона по времени обратим, так как, если повернуть время вспять, свою форму закон не изменит. Это означает, что и движение каждого отдельного шарика тоже обратимо: из конечного состояния шарика можно понять, откуда он пришел и как двигался, но… Но движение всех шариков вместе оказывается необратимым.
То есть в основе нашего необратимого мира лежат вполне себе обратимые законы. Это весьма странно. А что, если никакой необратимости нет, а это всего лишь иллюзия? Что, если движение просто настолько сложное, что оно кажется нам хаотичным, а на самом деле оно вполне регулярно?
Для примера того, что имеется в виду, возьмем очень интересную систему. Она называется клеточный автомат. Представьте, что ваша Вселенная — это простой ряд из белых и черных клеточек. Вы — бог этой Вселенной, и вам нужно заложить какое-то правило эволюции по времени. И вы закладываете очень простое правило: если сама клетка черная и соседние две клетки тоже черные, то в следующем шаге клетка будет белой (на картинке снизу слева), если клетка черная, сосед слева тоже черный, а сосед справа белый, то в следующем шаге клетка станет черной и так далее. Таким образом можно задать универсальное правило (физику) вашей Вселенной. Записать этот закон можно с помощью нулей и единичек или, если перевести их в десятиричную запись, с помощью просто одного числа. В данном случае (на картинке) это будет правило 90. Эволюция такого клеточного автомата показана ниже.
Таких правил существует очень много. Есть правила, которые опираются на два предыдущих шага вместо одного или на нескольких соседей. Есть правила для двумерного клеточного автомата, где у нас теперь не ряд из черных и белых клеточек, а целая плоскость.
С помощью клеточных автоматов уже получают совершенно сложные, непредсказуемые фигуры — их используют в архитектуре и игровом дизайне для построения реалистичного ландшафта. Но, что удивительно, все это разнообразие, эти непредсказуемые формы и образы задаются всего лишь правилом из одного числа, все остальное — дело времени.
Но что, если все разнообразие нашего мира, все сложные образы, создаваемые нашей природой, и весь тот хаос, к которому стремится наш мир, — это всего лишь реализация какого-то клеточного автомата? Что, если мы просто являемся симуляцией клеточного автомата в компьютере?
Как мы поняли в первой части, в самой глубокой основе нашего мира лежат вполне обратимые законы, где по конечному состоянию можно восстановить начальное. Поэтому если мир и есть клеточный автомат, то он должен также быть обратимым. Такие клеточные автоматы действительно есть, но у них есть одна проблема. У любого обратимого клеточного автомата есть цикл: через определенное число шагов Вселенная воссоздается в своем первоначальном виде снова, затем снова — и движется так по циклу.
В нашем мире, к сожалению, такого нет… Или есть? Французский математик Анри Пуанкаре для определенного типа систем заметил интересную вещь: в результате эволюции этих систем со временем они возвращались в свое первоначальное состояние, хотя изначально казалось, что стремятся они лишь в сторону хаоса. Такой цикл назвали циклом Пуанкаре.
Напрашивается очень интересная мысль. Да, действительно, газ из взорвавшегося гелиевого шарика в одну кучу обратно не соберется, но что, если подождать еще дольше? Что, если цикл Пуанкаре для такой системы очень большой? Есть целые космологические модели, основанные на гипотезе возврата Пуанкаре, одна из них принадлежит известному математику Пенроузу. По его мнению, Вселенная сначала раздувается, затем схлопывается обратно, затем снова взрывается, раздувается и вновь схлопывается, повторяя в точности предыдущий цикл.
Но у такой теории циклической Вселенной есть большой минус: мы пока не знаем процессов, способных заставить Вселенную схлопнуться. Где их искать? Так ли хорошо мы знаем нашу Вселенную? Данные телескопа Planck показали, что примерно 98% энергии нашей Вселенной не заключено в звездах и вообще в обычном веществе, из которого состоим мы. Мы с грехом пополам знаем лишь о 2% нашей Вселенной, а об остальных 98% не знаем вообще ничего. То есть если представить, что наша Вселенная — это большой прекрасный замок с башнями, мостами, тронными залами и прочим, то из подвала мы пока не выходили, и кто знает, какие тайны ждут нас там, наверху.
Вездесущая энтропия: от смерти Вселенной до груды грязной посуды
Михаил Петров
«Все процессы в мире происходят с увеличением энтропии» — эта расхожая формулировка превратила энтропию из научного термина в непреложное свидетельство обреченной борьбы человека с окружающим его беспорядком. Но что в оригинале скрывается за этой физической величиной? И как можно посчитать энтропию? «Теории и практики» попытались разобраться в этом вопросе и найти спасение от надвигающегося распада.
Термодинамика и «тепловая смерть»
Впервые термин «энтропия» в 1865 году ввел немецкий физик Рудольф Клаузиус. Тогда он имел узкое значение и использовался в качестве одной из величин для описания состояния термодинамических систем — то есть, физических систем, состоящих из большого количества частиц и способных обмениваться энергией и веществом с окружающей средой. Проблема заключалась в том, что до конца сформулировать, что именно характеризует энтропия, ученый не смог. К тому же, по предложенной им формуле можно было определить только изменение энтропии, а не ее абсолютное значение.
Упрощенно эту формулу можно записать как dS = dQ/T. Это означает, что разница в энтропии двух состояний термодинамической системы (dS) равна отношению количества тепла, затраченного на то, чтобы изменить первоначальное состояние (dQ), к температуре, при которой проходит изменение состояния (T). Например, чтобы растопить лед, нам требуется отдать ему некоторое количество тепла. Чтобы узнать, как изменилась энтропия в процессе таяния, нам нужно будет поделить это количество тепла (оно будет зависеть от массы льда) на температуру плавления (0 градусов по Цельсию = 273, 15 градусов по Кельвину. Отсчет идет от абсолютного нуля по Кельвину ( — 273° С ), поскольку при этой температуре энтропия любого вещества равна нулю). Так как обе величины положительны, при подсчете мы увидим, что энтропии стало больше. А если провести обратную операцию — заморозить воду (то есть, забрать у нее тепло), величина dQ будет отрицательной, а значит, и энтропии станет меньше.
Примерно в одно время с этой формулой появилась и формулировка второго закона термодинамики: «Энтропия изолированной системы не может уменьшаться». Выглядит похоже на популярную фразу, упомянутую в начале текста, но с двумя важными отличиями. Во-первых, вместо абстрактного «мира» используется понятие «изолированная система». Изолированной считается та система, которая не обменивается с окружающей средой ни веществом, ни энергией. Во-вторых, категорическое «увеличение» меняется на осторожное «не убывает» (для обратимых процессов в изолированной системе энтропия сохраняется неизменной, а для необратимых — возрастает).
За этими скучноватыми нюансами скрывается главное: второй закон термодинамики нельзя без оглядки применять ко всем явлениям и процессам нашего мира. Хороший тому пример привел сам Клаузиус: он считал, что энтропия Вселенной постоянно растет, а потому когда-нибудь неизбежно достигнет своего максимума — «тепловой смерти». Этакой физической нирваны, в которой не протекают уже никакие процессы. Клаузиус придерживался этой пессимистической гипотезы до самой смерти в 1888 году — на тот момент научные данные не позволяли ее опровергнуть. Но в 1920-х гг. американский астроном Эдвин Хаббл доказал, что Вселенная расширяется, а значит, ее
сложно назвать изолированной термодинамической системой. Поэтому современные физики к мрачным прогнозам Клаузиуса относятся вполне спокойно.
Энтропия как мера хаоса
Поскольку Клаузиус так и не смог сформулировать физический смысл энтропии, она оставалась абстрактным понятием до 1872 года — пока австрийский физик Людвиг Больцман не вывел новую формулу, позволяющий рассчитывать ее абсолютное значение. Она выглядит как S = k * ln W (где, S — энтропия, k — константа Больцмана, имеющая неизменное значение, W — статистический вес состояния). Благодаря этой формуле энтропия стала пониматься как мера упорядоченности системы.
Как это получилось? Статистический вес состояния — это число способов, которыми можно его реализовать. Представьте рабочий стол своего компьютера. Сколькими способами на нем можно навести относительный порядок? А полный беспорядок? Получается, что статистический вес «хаотичных» состояний гораздо больше, а, значит больше и их энтропия. Посмотреть подробный пример и рассчитать энтропию собственного рабочего стола можно здесь.
В этом контексте новый смысл приобретает второй закон термодинамики: теперь процессы не могут самопроизвольно протекать в сторону увеличения порядка. Но и тут не стоит забывать про ограничения закона.
Иначе человечество уже давно было бы в рабстве у одноразовой посуды. Ведь каждый раз, когда мы моем тарелку или кружку, нам на помощь приходит простейшая самоорганизация. В составе всех моющих средств есть поверхно-активные вещества (ПАВ). Их молекулы составлены из двух частей: первая по своей природе стремится к контакту с водой, а другая его избегает.
При попадании в воду молекулы «Фэйри» самопроизвольно собираются в «шарики», которые обволакивают частички жира или грязи (внешняя поверхность шарика это те самые склонные к контакту с водой части ПАВ, а внутренняя, наросшая вокруг ядра из частички грязи — это части, которые контакта с водой избегают). Казалось бы, этот простой пример противоречит второму закону термодинамики. Бульон из разнообразных молекул самопроизвольно перешел в некое более упорядоченное состояние с меньшей энтропией. Разгадка снова проста: систему «Вода-грязная посуда после вечеринки», в которую посторонняя рука капнула моющего средства, сложно считать изолированной.
Черные дыры и живые существа
Со времен появления формулы Больцмана термин «энтропия» проник практически во
все области науки и оброс новыми парадоксами. Возьмем, к примеру астрофизику и пару «черная дыра — падающее в нее тело». Ее вполне можно считать изолированной системой, а значит, ее энтропия такой системы должна сохраняться. Но она бесследно исчезает в черной дыре — ведь оттуда не вырваться ни материи, ни излучению. Что же происходит с ней внутри черной дыры?
Некоторые специалисты теории струн утверждают, что эта энтропия превращается в энтропию черной дыры, которая представляет собой единую структуру, связанную из многих квантовых струн (это гипотетические физические объекты, крошечные многомерные структуры, колебания которых порождают все элементарные частицы, поля и прочую привычную физику). Впрочем, другие ученые предлагают менее экстравагантный ответ: пропавшая информация, все-таки возвращается в мир вместе с излучением, исходящим от черных дыр.
Еще один парадокс, идущий вразрез со вторым началом термодинамики — это существование и функционирование живых существ. Ведь даже живая клетка со всеми ее биослоями мембран, молекулами ДНК и уникальными белками — это высокоупорядоченная структура, не говоря уже о целом организме. За счет чего существует система с такой низкой энтропией?
Точнее организм питается углеводами, белками и жирами. Высокоупорядоченными, часто длинными молекулами со сравнительно низкой энтропией. А взамен выделяет в окружающую среду уже гораздо более простые вещества с большей энтропией. Вот такое вечное противостояние с хаосом мира.