есть что то больше бесконечности
Какое оно число, что больше бесконечности?
«Две вещи действительно бесконечны: Вселенная и человеческая глупость. Впрочем, насчет Вселенной у меня есть некоторые сомнения». Альберт Эйнштейн
Знак бесконечности имеет разные сферы применения. Многие впервые знакомятся с ним на уроках математики, а еще его используют в физике, логике, философии. Характеризуют его различными неисчисляемыми объектами, у которых нет размера и границ. Современная молодежь символ знака бесконечности использует для украшения своего тела в виде татуировки. Впервые этот знак изобразил математик Джон Валлис в 1655 году. Немного позднее, в 1694 г. швейцарский математик Якоб Бернулли в своей статье опубликовал изображение знака бесконечности, демонстрирующего описанную им плоскую алгебраическую кривую, и назвал его «лемнискатой». С тех пор в мире науки данную фигуру именуют «лемнискатой Бернулли». Так в Древней Греции именовали специальное крепление в виде бантика для венка, победителей в спортивных состязаниях.
По одной из исторических теорий, знак бесконечности был перемещён в современную западную цивилизацию из индийской культурной традиции. По другой версии история зарождения символа бесконечности своими корнями уходит к наскальным изображениям в Тибете. В общем, на сегодняшний день нет точной информации, почему был выбран именно такой символ.
Израильский математик, профессор Дорон Зельбергер, убеждён, что числа не могут увеличиваться бесконечно, и существует такое огромное число, что если прибавить к нему единицу, получится ноль.
Возможно, это число и его значение лежат далеко за пределами человеческого понимания, и вероятно, это число никогда не будет найдено и доказано. Но почему тогда многие так легко оперируют со словом бесконечность, как будто это число?
Некоторые народы до сих пор используют простейшие системы записи чисел. Например, племя Пираха, живущее в Амазонии, применяет очень простую систему нумералов: один, два, много. Пираха не знают чисел больше двух, и у них такие операции, как 2+1 и 2+2, дают одинаковый результат, то есть «много». Они не в состоянии различать числа 3 и 4, не могут выполнять арифметические операции c ними и в целом не в состоянии сказать что-либо об этих числах, поскольку в их языке нет ни слов, ни концепций для этого.
Как посчитать сверх бесконечности?
Если вы сразу не поняли о чем я, не удивляйтесь, я сам не понимал.
Бесконечность это число у которого НЕТ КОНЦА. Значит нету ничего больше бесконечности? Не совсем.
С названиями разобрались, давайте разберемся как эти числа устроины.
Алеф нуль и омега это бесконечность, только к которым можно прибавлять. Омега обычно применяется для нумерации, новых степеней и т.д.
Надеюсь вы поняли. В следующих постах я буду писать подробнее и понятней.
Я не берусь судить о достоверности. Просто за каким хером оно все надо?
а если Тэтта в степени Тэтта высотой башни Тэтта раз ответ в степени ответа ответ раз и так далее конечного ответа раз тоесть даже недостижимый кординал в степени недостижимого кординала недостижимый кординал раз это число капля в мировом океане планеты нептун. так что это число меньше алефануль вот только незадача число алефнуль увеличился в объёме. но вот незадача число моё тоже увеличилось в объеме. моё число ПЕРЕДОСТИГНУТЫЙ КОРДИНАЛ
Вообще-то, кардиналы и кардинальные числа — правильно написанные слова. Так что гуляй, гуманитарная маня!
где это применяется.
А почему «Алеф» и «Омега»? Обычно для родственных вещей в математике используют один и тот же алфавит.
Бесконечность даже не число.
И бесконечности бывают разные.
Кущевская ОПГ
Кущевская резня, Ростов, 11 лет прошло и все по кругу, просто нет комментариев, предлагаю поднять резонанс, что бы такой беспредел не замолчали.
Бесплатное кино
Буквально сегодня столкнулся с ситуацией, которую не хотел бы видеть. Еду в электричке на ночную смену. Фрязинское направление, первый вагон, время около 21:30. Все едут по своим делам, залипают в телефонах. Вот он появляется. Главный подмосковный жених.
Правда глаза режет
Если вдруг кто не в курсе то этот самый султан проталкивает закон о запрете называть национальность,мол у людей плохое мнение сразу складывается.
Видать правда глаза режет.
Собакодевочка
И стало так хорошо.
Про «национальность, которой нет»
Всем привет. Пишу сюда первый раз. Но сейчас не об этом
Я журналист. И смею заметить, что СМИ не указывают национальность правонарушителя. СМИ пишут «уроженец Дагестана», «житель Оренбурга», «трудовой мигрант из Таджикистана» и т.д. Национальность не указывается. Так что все эти вопли по поводу «а давайте запретим указывать национальность» ни о чем.
Правильная штопка
Так происходит эвтаназия в Швейцарии, для человека с неизлечимым заболеванием
Фильм «Терри Пратчетт: Выбирая умереть»
Бывает
Скафандр
Осталось 10 дней
Вот работаешь, а тебя делают крайним
В Казани умер человек, в смерти обвиняют рентгенолога, который просто сделал описание КТ лёгких. А после этого КТ человек лечился ещё в нескольких больницах и делал ещё КТ, но умер.
Рентгенолог не лечил пациента, не решал вопросы маршрутизации.
Само открытое письмо.
Уважаемые коллеги-рентгенологи и врачи г. Казани и Республики Татарстан.
К Вам обращается Самигуллин Максим Александрович, 1983 года рождения, работающий врачом-рентгенологом отделения лучевой диагностики ГАУЗ «МКДЦ» МЗ РТ, что находится по адресу: г. Казань, ул. Карбышева 12а.
В настоящее время в СК по Приволжскому району г. Казани в отношении меня возбуждено уголовное дело №12002920007000494 от 11.11.2020 по признакам преступления предусмотренного ч.2 ст.109 УПК РФ – причинение смерти по неосторожности (до 4 лет лишения свободы).
Меня обвиняют в причинении смерти по неосторожности пациенту Аминову А.А., которого я лично не знал, решений касательно его здоровья, лечения и маршрутизации не принимал. Я только вынес заключение по данным рентгеновской компьютерной томографии от 15.07.2020, проведенной в ГАУЗ «МКДЦ» МЗ РТ, о вероятности того, что выявленные изменения в легких могли быть обусловлены вирусным поражением, в том числе и КОВИД-19. После чего, спустя 2 недели, пациент Аминов А.А., побывав в 4 больницах г. Казани, и пройдя еще 2 раза РКТ ОГК (не в МКДЦ), скончался.
СК по Приволжскому району г. Казани, следователи Хасаншин И.М. и Сулейманова В.Т., имея на руках все факты, касательно этого случая, безосновательно и предвзято предъявили мне тяжкие обвинения, попутно очернив мою репутацию в материалах дела.
Свои обвинения они основывают только на заключении судмедэксперта Хабибулиной С.Ш., которая заявила о моей неверной интерпретации данных рентгеновской компьютерной томографии пациента Аминова А.И. от 15.07.2021. Хотя все, более высококвалифицированные чем она, приглашенные независимые эксперты (Закиров Р.Х., Курочкин С.В., Анисимов В.И., Рафиков А.Ю – люди хорошо известные рентгенологическому сообществу г. Казани и Республики Татарстан) заявили свое несогласие с ее описанием и доводами о неверной интерпретации снимков Самигуллиным М.А. Показания данных экспертов приобщены у уголовному делу. К тому же они проводили оценку данных томограмм незамутненным взглядом, а эксперт Хабибулина С.Ш. сама указала на допросе, что она больше опиралась, вынося заключение, на данные посмертного гистологического исследования. (При этом надо отметить, что все эксперты оценивали патологические изменения в легких в динамике на основании данных 3 РКТ ОГК, в отличии от меня, когда я проводил пациенту Аминову 1 РКТ ОГК 15.07.2021).
На основании единственного заключения судмедэксперта Хабибуллиной следователи, невзирая на все остальные доводы и вопросы защиты к экспертизе, которые были отражены в отклоненном СК ходатайстве, делают все возможное для скорейшей передачи дела в суд.
Виновным в преступлении себя не признаю, считаю свои действия в данном конкретном случае верными поскольку всегда поступал по совести, руководствуясь своим долгом и клятвой врача. Отдельно хочу ответить, что подобная несправедливость происходит во время очередной волны коронавирусной инфекции, захлестнувшей нашу страну, когда все медработники и система здравоохранения работают на пределе своих возможностей.
Хочу, чтобы Вы – коллеги были в курсе данной ситуации и в полной мере осознали насколько в тяжелой нынешней ситуации Вы «ценны» для системы здравоохранения и правопорядка, когда с экранов телевизора и со страниц газет Вам вещают о героях врачах, в которых нуждается Родина, а с другой стороны на Вас пытаются «повесить» уголовное преступление, не имея оснований и бездоказательно. На моем месте в любой момент может оказаться любой из вас.
Что больше? Бесконечность или две бесконечности?
В современной математике нет определения бесконечности. Есть символ ∞, который читается «бесконечность», но обозначают этим символом разное. Поэтому ответ зависит от того, что подразумевается под этим словом.
Когда-то в XVIII, XIX веках с бесконечностью обращались вольнее, но со временем математики выяснили, что вольное обращение приводит к парадоксам. Поэтому словоупотребление и символы оставили, а смыслы уточнили. Сейчас, когда математики говорят «бесконечность», они подразумевают понятия, которые строго определяются без этого слова.
Прежде чем рассматривать бесконечность-другую, надо уточнять, что именно имеется в виду.
Например, мы привыкли к пределам «при n, стремящемся к бесконечности». Но эти слова не означают, что существует какая-то бесконечность. Они означают длинное условие (для любого ε>0 существует такое N, что для всех n>N…) и подразумевают замысловатую абстрактную конструкцию.
Одно из распространенных пониманий бесконечности — обозначение мощности бесконечного множества. Возьмем четные натуральные числа 2, 4, 6, 8… и нечетные 1, 3, 5, 7, … Каких больше? Эти множества равномощны, ведь мы можем установить соответствие как на картинке:
Для каждого нечетного числа укажем четное и наоборот; в этом смысле четных и нечетных чисел «поровну». Это «поровну» не означает равное количество, ведь и тех и других бесконечно много.
Возьмем да и объединим четные числа с нечетными в одно множество — получатся натуральные числа 1, 2, 3, 4, 5, 6, 7, …
Если бы объединяли конечные множества, скажем, в одном 3 элемента, в другом 4, то в общей кучке количество элементов — это сумма 3+4, или 7. Поэтому может показаться, что когда объединили бесконечно много четных чисел и бесконечно много нечетных, то получится две бесконечности.
На самом деле не получится, хотя это и противоречит нашей интуиции. Натуральных чисел ровно «столько же», сколько четных, ведь мы можем опять построить соответствие:
Здесь каждому натуральному числу соответствует четное и наоборот. Значит, множества натуральных чисел и четных равномощны.
Мы объединили два разных бесконечных множества и получили одно, равномощное им. В этом смысле две бесконечности не больше одной; но это был лишь маленький пример. Есть много других пониманий бесконечности, сложения бесконечностей или сравнения бесконечностей.
Какое наибольшее число перед бесконечностью?
Мы можем написать гугол, используя экспоненты, сказав, что гугол равен 10 ^ 100.
Это записывается как единица, за которой следуют нули гугола.
Какое число выше бесконечности?
Согласно этому определению, нет ничего (что означает: никаких действительных чисел) больше бесконечности. Есть другой способ взглянуть на этот вопрос. Это возникло из идеи Георга Кантора, который жил с 1845 по 1918 год. Кантор сравнивал размер двух наборов, то есть двух коллекций вещей.
Какое число прямо перед бесконечностью?
Одно называлось «пси», и предполагалось, что оно будет «последним» конечным числом, то есть числом непосредственно перед бесконечностью. Второе называлось «конечным числом», которое считается самым высоким в царстве чисел. Нет ничего больше, чем конечное число, потому что по определению это последнее число.
Какое наибольшее число известно человеку?
Число Грэма больше бесконечности?
Любое конечное число бесконечно отличается от бесконечности. Даже такое огромное число, как число Грэма, намного меньше, чем, скажем, или. И просто составить еще большие числа, которые заставят их выглядеть незначительными, и все они меньше, чем пятнышко по сравнению с бесконечностью.
Сколько времени нужно, чтобы считать до бесконечности?
Вы можете придумать ситуацию, когда вам понадобится одна секунда, чтобы произнести первое число, а затем каждый раз, когда вы произносите число, вы будете считать в два раза быстрее. Затем потребуется две секунды, чтобы считать до бесконечности. Для нормального человека это займет бесконечное количество времени, которого у нас нет, поэтому это невозможно.
Какое число за гранью бесконечности?
Заканчиваются ли числа когда-нибудь?
Последовательность натуральных чисел бесконечна и бесконечна. Нет причин, по которым тройки должны когда-либо останавливаться: они повторяются бесконечно. Итак, когда мы видим такое число, как «3» (то есть десятичное число с бесконечной серией девяток), количеству девяток нет конца.
Заканчиваются ли числа да или нет?
Нет, счету чисел 1, 2, 3 и так далее нет конца. Это не может быть самое большое число, потому что вы можете просто добавить 1 к 11 и получить большее число, а именно 12. И так далее, и так далее. Общая идея состоит в том, что для любого данного числа всегда есть более крупный сосед.
Есть ли у Infinity число?
Что такое гуголплексиант?
Является ли наибольшее число бесконечностью?
Число Грэма невероятно огромно. самое большое известное нам простое число, состоящее из 17,425,170 10100 1 цифр. И он больше, чем знаменитый гугол, 100 (1929, за которым следуют XNUMX нулей), который был определен в XNUMX году американским математиком Эдвардом Каснером и назван его девятилетним племянником Милтоном Сироттой.
Какое самое маленькое число в мире?
Можем ли мы понять бесконечность?
Сколько времени нужно, чтобы потратить триллион долларов?
Сколько времени нужно, чтобы пересчитать миллион долларов вручную?
Чтобы сосчитать до миллиона, нужно около месяца! Но на то, чтобы сосчитать до 25, потребовалось всего 100 секунд, а числа быстро становятся большими! (Даже если бы вы могли считать без перерывов и с той же скоростью, что и до 100, это все равно заняло бы почти 70 часов.)
Какое наибольшее число кто-то посчитал?
Гуголплекс больше бесконечности?
Омега выше бесконечности?
Алеф Нуль больше бесконечности?
Есть ли у бесконечности начало?
На самом деле все зависит от описываемой вами бесконечности, будет ли у нее начало или нет. У большинства бесконечностей действительно есть начала просто потому, что для того, чтобы ощутить концепцию той бесконечности, о которой мы говорим (просто исходя из ограничений человеческого разума), нам обычно нужна отправная точка.
Сколько нулей в бесконечности?
Сколько существует уровней бесконечности?
Однако не все бесконечные множества созданы равными. На самом деле существует множество различных размеров или уровней бесконечности; некоторые бесконечные множества намного больше, чем другие бесконечные множества. Теория бесконечных множеств была разработана в конце девятнадцатого века блестящим математиком Георгом Кантором.
Какое оно, число, что больше бесконечности?
Понедельник! Пора сломать мозг!
«Две вещи действительно бесконечны: Вселенная и человеческая глупость. Впрочем, насчет Вселенной у меня есть некоторые сомнения». Альберт Эйнштейн
Знак бесконечности имеет разные сферы применения. Многие впервые знакомятся с ним на уроках математики, а еще его используют в физике, логике, философии. Характеризуют его различными неисчисляемыми объектами, у которых нет размера и границ. Современная молодежь символ знака бесконечности использует для украшения своего тела в виде татуировки. Впервые этот знак изобразил математик Джон Валлис в 1655 году. Немного позднее, в 1694 г. швейцарский математик Якоб Бернулли в своей статье опубликовал изображение знака бесконечности, демонстрирующего описанную им плоскую алгебраическую кривую, и назвал его «лемнискатой». С тех пор в мире науки данную фигуру именуют «лемнискатой Бернулли». Так в Древней Греции именовали специальное крепление в виде бантика для венка, победителей в спортивных состязаниях.
По одной из исторических теорий, знак бесконечности был перемещён в современную западную цивилизацию из индийской культурной традиции. По другой версии история зарождения символа бесконечности своими корнями уходит к наскальным изображениям в Тибете. В общем, на сегодняшний день нет точной информации, почему был выбран именно такой символ.
Израильский математик, профессор Дорон Зельбергер, убеждён, что числа не могут увеличиваться бесконечно, и существует такое огромное число, что если прибавить к нему единицу, получится ноль.
Насчёт единицы не уверен. В тему сильно не углублялся, но сдаётся мне, что на множестве натуральных чисел такое может не проканать (не знаю).
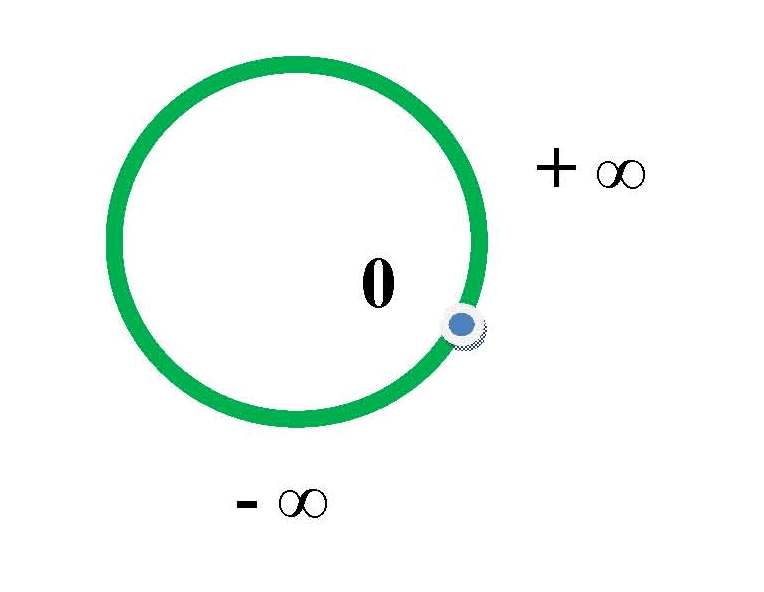
А вот с рациональными.
Ну а здесь можно для наглядности почитать про Риманову геометрию, чтобы представить себе такое. Если влом, то посмотрите на глобус, там есть геодезические кривые и полюса (плоскоземельщикам не читать).
И картинку посмотреть:
Возможно, это число и его значение лежат далеко за пределами человеческого понимания, и вероятно, это число никогда не будет найдено и доказано. Но почему тогда многие так легко оперируют со словом бесконечность, как будто это число?
Некоторые народы до сих пор используют простейшие системы записи чисел. Например, племя Пираха, живущее в Амазонии, применяет очень простую систему нумералов: один, два, много. Пираха не знают чисел больше двух, и у них такие операции, как 2 1 и 2 2, дают одинаковый результат, то есть «много». Они не в состоянии различать числа 3 и 4, не могут выполнять арифметические операции c ними и в целом не в состоянии сказать что-либо об этих числах, поскольку в их языке нет ни слов, ни концепций для этого.
1. Актуальная бесконечность существовать не может.
2. Безначальный ряд временных событий представляет собой актуальную бесконечность.
3. Следовательно, безначальный ряд временных событий не может существовать.
Рассмотрим вначале первую посылку: Актуальная бесконечность не может существовать.
Что я имею в виду под актуальной бесконечностью? Множество объектов считается актуально бесконечным, если часть этого множества равна его целому. Так например, какой рад длиннее:
По общепринятым математическим представлениям, эти ряды эквивалентны, потому что они оба актуально бесконечны. Это кажется странным: ведь в правом ряду есть два числа, отсутствующие в левом. Но это лишь показывает, что в актуально бесконечном множестве часть (левый ряд) равна целому (правый ряд).
По той же причине математики утверждают, что ряд чётных чисел равен ряду натуральных чисел — несмотря на то, что ряд всех натуральных чисел содержит все чётные плюс бесконечное число нечётных чисел.
При этом не надо смешивать понятия актуальной бесконечности — и потенциальной бесконечности.
По мнению великого немецкого математика Давида Гилберта, главное различие между актуальной и потенциальной бесконечностью заключается вот в чём. Потенциально бесконечное есть всегда нечто возрастающее и имеющее пределом бесконечность, тогда как актуальная бесконечность — это завершённое целое, в действительности содержащее бесконечное число предметов.
Интересным примером этих двух типов бесконечности могут послужить два ряда событий: произошедших до и после какой-либо точки в прошлом.
Возьмём, например, момент в 1845 г., когда родился Георг Кантор, отец теории множеств.
В обоих случаях мы имеем в виду события, действительно случившиеся.
Точка, называемая «настоящее время», разумеется, не стоит на месте, а скользит вперёд. (По сути дела, это граница между событиями уже реализованными и ещё не реализованными.) Поэтому количество событий «после» (т. е. между 1845 г. и настоящим временем), хотя и в каждый конкретный момент конечное, постоянно возрастает. Оно никогда не реализовано до конца, и потому потенциально бесконечно.
Но ряд событий «до» полностью реализован, завершён и не возрастает. И если атеисты правы, и у Вселенной не было начала, то такой ряд бесконечен. Бесконечен актуально, реально.
В ходе наших рассуждений очень важно эти два понятия (актуальной и потенциальной бесконечности) не путать.
Второе пояснение касается слова «существовать». Когда я говорю, что актуальная бесконечность не может существовать, я имею в виду — существовать в реальном мире, или существовать не только в уме. Я вовсе не отрицаю законность использования понятия актуальной бесконечности в математике (оперирующей лишь мысленной реальностью). Я лишь утверждаю, что актуальная бесконечность не может существовать в физическом мире звёзд, планет, камней и людей.
Несколько примеров покажут абсурдность такого допущения.
Допустим, что существует библиотека, содержащая реально бесконечное число книг. Представим себе, что книги в ней только двух цветов, чёрного и красного, и что они стоят на полках, чередуясь: чёрная, красная, чёрная, красная, и т.д. Если кто-то скажет нам, что число чёрных книг равно числу красных, мы, вероятно, не удивимся. Но поверим ли мы, если нам скажут, что число чёрных книг равно числу чёрных и красных книг вместе? Ведь в таком собрании мы обнаружим все чёрные книги плюс бесконечное число красных книг!
Или же представим себе, что у нас есть книги трёх цветов, четырёх, пяти или даже ста. Поверим ли мы, что книг одного цвета столько же, сколько всего книг в библиотеке?
Несколько примеров покажут абсурдность такого допущения.
Допустим, что существует библиотека, содержащая реально бесконечное число книг. Представим себе, что книги в ней только двух цветов, чёрного и красного, и что они стоят на полках, чередуясь: чёрная, красная, чёрная, красная, и т.д. Если кто-то скажет нам, что число чёрных книг равно числу красных, мы, вероятно, не удивимся. Но поверим ли мы, если нам скажут, что число чёрных книг равно числу чёрных и красных книг вместе? Ведь в таком собрании мы обнаружим все чёрные книги плюс бесконечное число красных книг!
Или же представим себе, что у нас есть книги трёх цветов, четырёх, пяти или даже ста. Поверим ли мы, что книг одного цвета столько же, сколько всего книг в библиотеке?
Продолжим наши рассуждения. Предположим, что у каждой книги на корешке отпечатан номер. Поскольку библиотека реально бесконечна, каждое возможное число отпечатано на какой-либо из книг. Поэтому мы не можем добавить к библиотеке ещё одну книгу, ибо какой номер ей дать? Всё номера уже заняты. Таким образом, новой книге нельзя дать номера! Но это абсурд, так как в действительности предметы всегда можно нумеровать.
Если бы бесконечная библиотека существовала, то к ней невозможно было бы добавить ещё одну книгу. (Не потому ли, что она уже включала бы все существующие книги, и новую просто неоткуда было бы взять? Нет, ведь достаточно вырвать по листку из каждой книги первой сотни, склеить их вместе, поставить эту новую книгу на полку, и всё — библиотека пополнена!) Поэтому напрашивается единственно возможный вывод: библиотека, актуально бесконечная, — существовать не может.
Но предположим, что мы можем пополнить эту библиотеку, и я ставлю книгу на полку. По утверждению математиков, число книг в библиотеке осталось прежним. Как это может быть? Ведь мои опыт говорит: если я поставил книгу на полку, то там стало книгой больше, а если снял, то одной меньше.
Мне легко вообразить себя, ставящего и снимающего эту книгу. Должен ли я впрямь всерьёз поверить, что когда я добавляю книги, их число не увеличивается, а когда убираю — не уменьшается? А если я добавлю к этой библиотеке бесконечное число или даже бесконечность бесконечностей книг? Неужели и теперь в библиотеке ни на одну книгу не больше, чем прежде? Мне в это трудно поверить. А вам?
А теперь давайте, наоборот, выдавать книги из библиотеки. Предположим, в понедельник мы выдали книгу номер восемь. Разве число книг не уменьшилось на одну?
Во вторник — выдадим все книги с нечётными номерами. Ушло бесконечное число книг, но математики скажут, что в библиотеке книг меньше не стало.
Допустим, что в среду мы выдали книги за номерами 4, 5, 6. и до бесконечности. Единым махом библиотека практически вся опустела, бесконечное число книг сведено к конечному: к трём. Но позвольте, ведь мы на этот раз выдали столько же книг, что и во вторник! Почему же такая разница? И кто поверит, что такая библиотека может на самом деле существовать?
Все эти примеры иллюстрируют тот факт, что актуальная бесконечность не может иметь места в физическом мире. Я вновь хочу подчеркнуть: это ничем не грозит теоретической системе, введённой в современную математику Г. Кантором. Больше того: даже такие энтузиасты математических теорий бесконечного, как Д. Гилберт, охотно соглашаются с тем, что понятие актуальной бесконечности — это только идея, не имеющая никакого отношения к реальному миру.Поэтому — мы вправе заключить: актуальная бесконечность существовать не может.
Вторая посылка: Ряд событий во времени, не имеющий начала, представляет собой актуальную бесконечность.
Под «событием» я подразумеваю любую перемену, происходящую в физическом мире. То есть: если ряд прошлых событий (или перемен) всё время уходит в прошлое и никогда не имеет начала, то в этом случае, взятые все вместе, эти события составляют актуально бесконечное множество.
Допустим, мы спрашиваем, откуда появилась такая-то звезда. Нам отвечают, что она появилась в результате взрыва звезды, существовавшей до этого. Тогда мы спрашиваем, откуда появилась та звезда? Она тоже возникла из звезды, существовавшей до неё. А эта звезда откуда? Из другой, предыдущей звезды — и так далее. Этот ряд звёзд будет примером безначального во времени ряда событий.
Тогда, если Вселенная существовала всегда, ряд всех событий прошлого в их совокупности составит актуальную бесконечность: потому что каждому событию в прошлом предшествовало другое событие. Таким образом, ряд прошлых событий будет бесконечным.
Но не будет ли он потенциально бесконечным? Нет, ибо мы видели, что прошлое завершено и актуально, — лишь будущее может быть охарактеризовано как потенциально бесконечное. Поэтому представляется очевидным, что безначальный ряд событий во времени является актуальной бесконечностью.
Это приводит нас к нужному заключению. безначальный ряд событий во времени существовать не может. (Мы установили ранее, что актуально бесконечное не может существовать в действительности. И если безначальный ряд временных событий есть актуальная бесконечность, то такой ряд не может существовать.)
Значит, ряд всех событий прошлого обязан иметь начало. Но ведь история Вселенной и есть ряд всех свершившихся событий! Поэтому у Вселенной должно быть начало.
Несколько примеров пояснят этот аргумент.
Мы знаем, что если бы актуальная бесконечность могла существовать в действительности, к ней невозможно было бы ничего прибавить. Но к ряду событий во времени происходят добавления каждый день — или, по крайней мере, нам так кажется. Если же этот ряд актуально бесконечен, то число событий, случившихся до настоящего момента, — не больше, чем, скажем, число событий до 1789 года или до любой другой точки в прошлом, сколь угодно далёкой.
Ещё пример. Вообразим, что вокруг Солнца уже целую вечность вращаются две планеты. Допустим, что одна проходит свою орбиту за три года, другая — за год. Таким образом, на каждый оборот одной приходятся три оборота другой. Вопрос: если они движутся вечно, которая из этих планет сделала больше орбитных оборотов? Ответ: обе сделали одинаковое число оборотов. Но это явный абсурд, ведь здравый смысл подсказывает: чем дольше они вращаются, тем сильнее увеличивается разрыв. Как же может число оборотов быть равным?
Эти примеры подчёркивают абсурдность идеи безначального ряда событий во времени. Поскольку такой ряд является актуально бесконечным, а актуальная бесконечность существовать не может, то и этот ряд невозможен. Это значит, что Вселенная когда-то начала своё существование, что и требовалось доказать.