Формула бабине для чего
Барометрическая ступень
Барометри́ческая ступе́нь (бари́ческая ступе́нь) — величина, определяющая изменение высоты в зависимости от изменения атмосферного давления. Применяется при барометрическом нивелировании и при пересчёте показаний статоскопа в разность высот.
Зависит от давления и температуры воздуха.
Наглядный смысл барометрической ступени — высота, на которую надо подняться, чтобы давление понизилось на 1 гПа.
Содержание
Применение

Формула практически точна при небольших (десятки метров) изменениях высоты.
Вычисление барометрической ступени

Таблица величины барометрической ступени (м/кПа) для некоторых значений давления и температуры:
| Давление, кПа | Температура, °C | ||||
|---|---|---|---|---|---|
| −40 | −20 | 0 | 20 | 40 | |
| 100 | 67 | 74 | 80 | 86 | 93 |
| 50 | 134 | 147 | 160 | 173 | 186 |
| 10 | 672 | 736 | 800 | 864 | 928 |
Пример
При переносе барометра с уровня моря на холм давление уменьшилось на 2 мм.рт.ст. Температура комнатная. Какова высота холма?
1 мм.рт.ст = 101,325/760 мм = 0.13332 кПа.
Положим, что давление на уровне моря равно стандартному:
Δp = — 2 мм.рт.ст. = — 2 • 0,13332 кПа/мм.рт.ст = — 0,26664 кПа
Из формулы: Q = 84.7 м/кПа (или 11.29 метра на 1 мм.рт.ст).
Изменение высоты (высота холма) Δh = 84.7 • 0,26664 = 22,59 ≈ 22,6 метра
Разницу можно вычислить также по барометрической формуле: Δh = 18400*(1 + a*t)*lg (p1 / p2) (в метрах), где t — средняя температура слоя воздуха между точками измерения в градусах, a — температурный коэффициент объёмного расширения воздуха 0.00366. Или 18400*(1 + 0.00366*20)*lg (760 / (760+2 мм)) = 22.54 метра.
См. также
Литература и ссылки
Полезное
Смотреть что такое «Барометрическая ступень» в других словарях:
Барометрическая ступень — то же, что Барическая ступень … Большая советская энциклопедия
Барометрическая формула — Барометрическая формула зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения… … Википедия
Барическая ступень — барометрическая ступень, разность высот двух точек на одной вертикали, соответствующая разности атмосферного давления в 1 мбар между этими точками (1 мбар = 100 н/м2). Б. с. тем больше, чем ниже давление. Поэтому с высотой она… … Большая советская энциклопедия
барическая ступень высоты — барическая ступень Ндп. барометрическая ступень Расстояние по вертикали, соответствующее изменению атмосферного давления на единицу. [ГОСТ 22268 76] Недопустимые, нерекомендуемые барометрическая ступень Тематики геодезия Обобщающие термины… … Справочник технического переводчика
Барическая ступень высоты — 99. Барическая ступень высоты Барическая ступень Ндп. Барометрическая ступень D. Barometrische Höhenstufe E. Barometric height increment F. Échelon de pression d altitude Расстояние по вертикали, соответствующее изменению атмосферного давления на … Словарь-справочник терминов нормативно-технической документации
ГОСТ 22268-76: Геодезия. Термины и определения — Терминология ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа: 114. Абрис Ндп. Кроки D. Gelandeskizze Gelandekroki E. Outline Field sketch F. Croquis Схематический чертеж участка местности Определения термина из разных документов … Словарь-справочник терминов нормативно-технической документации
Принцип Бабине
Принцип Бабине (также теорема Бабине ) является предложением оптики и утверждает, что дифракционные изображения двух взаимодополняющих диафрагм ( например, щелевой диафрагмы и проволоки одинаковой толщины) находятся за пределами области, на которую попадает геометрическо-оптическое изображение (т. Е. рисунок без дифракционных эффектов), то же самое. Например, дифракционная картина отдельной щели практически не отличается от дифракционной картины от проволоки, а дифракционная картина круглого диска не отличается от дифракционной картины по размеру круга.
Название восходит к французскому физику Жаку Бабине (1794–1872), который сформулировал теорему в 1837 году.
Оглавление
Объяснение и применение
Принцип, установленный Бабине в 1837 году, теперь гласит, что взаимно дополняющие апертуры, то есть апертуры, в которых отверстия и непрозрачные области меняются местами, создают одинаковые дифракционные явления за пределами области, которую занимало бы геометрическо-оптическое изображение.
Применение в электродинамике
По аналогии с оптикой, принцип Бабине можно использовать и в электродинамике, так что получаются полезные соотношения. Например, электромагнитные эффекты могут быть рассчитаны через отверстия в проводящих плоскостях. Знания касательных к поверхности электрических полей достаточно для расчета полей, прошедших через отверстие. Например, его можно использовать для определения электромагнитного поля отверстия на бесконечно протяженной проводящей поверхности, в которой невозможно рассчитать распределение тока. По принципу Бабине отверстие становится проводящей поверхностью. В этом случае поверхностные токи должны быть рассчитаны только по отверстию, и обратное преобразование, наконец, дает результат для отверстия на бесконечно большой проводящей поверхности.
Вывод
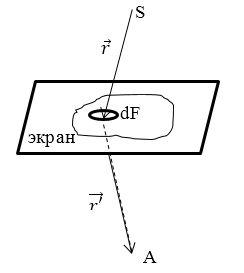
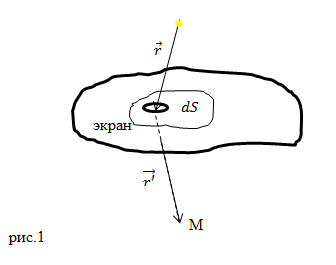
Однако и точечное отверстие, и непрозрачное препятствие естественным образом создают дифракционную картину. Для этих дифракционных картин от точечного отверстия и препятствия амплитуда, падающая на экран, может быть разбита на геометрическую и дифракционную составляющие:
(3) Э. отверстие ( Икс ) + Э. задняя ( Икс ) знак равно Э. 0 ( Икс ) <\ displaystyle E _ <\ text
(4) Э. Лохгео ( Икс ) + Э. индеец ( Икс ) знак равно Э. 0 ( Икс ) <\ displaystyle E _ <\ text
Если теперь установить уравнение. (1) и (2) в уравнении. (3) получаем:
(5) Э. отверстие ( Икс ) + Э. задняя ( Икс ) знак равно Э. Лохгео ( Икс ) + Э. изгиб отверстий ( Икс ) + Э. индеец ( Икс ) + Э. задница ( Икс ) знак равно Э. 0 ( Икс ) <\ displaystyle E _ <\ text
С формулой. (4) приводит к:
Фраунгофера дифракция
Расширение до размеров векторного поля
Описанные выше дифракционные явления относятся к величине электрических полей или распределению интенсивности дифрагированного электромагнитного излучения. Они получены (как и выше) в рамках приближений дифракционного интеграла Кирхгофа для размеров скалярного поля. Если кто-то хочет сделать выводы о комплексных электрических и магнитных полях и свойствах поляризации, он обычно ограничивается случаем диафрагм, сделанных из бесконечно тонких и идеально электропроводящих материалов. В случае, если компоненты электрического и магнитного поля падают перпендикулярно диафрагмам, следует отметить, что при переключении между дополнительными диафрагмами векторы поля должны быть повернуты на 90 ° вокруг нормали к поверхности. Для получения информации о направлении вращения и других подробностях см. Данные ссылки и учебник « Классическая электродинамика » Дж. Д. Джексона. Электрические дипольные моменты одной диафрагмы становятся магнитными дипольными моментами дополнительной диафрагмы и наоборот.
Лейкоцитарная формула с обязательной «ручной» микроскопией мазка крови (капиллярная кровь) (капиллярн. кровь) в Покрова
Определение лейкоцитарной формулы позволяет выявить изменение количества лейкоцитов, а также обнаружить молодые и патологические формы лейкоцитов.
Приём и исследование биоматериала
Когда нужно сдавать анализ Лейкоцитарная формула с обязательной «ручной» микроскопией мазка крови (капиллярная кровь)?
Подробное описание исследования
Лейкоцитарная формула — процентное соотношение различных видов лейкоцитов. При заболеваниях, патологических состояниях происходит ее неспецифичное изменение, что позволяет судить о переменах в организме.
Лейкоциты, или белые кровяные тельца:
Лейкоциты по строению подразделяются на зернистые (гранулоциты) и незернистые (агранулоциты). Такие названия даны из-за наличия специфической зернистости в цитоплазме и присутствия определенной сегментации ядра.
Подсчет лейкоцитарной формулы проводится как анализатором (который способен оценить несколько тысяч клеток), так и методом ручной микроскопии, при котором врач просматривает клетки самостоятельно. Это позволяет выявить молодые и патологические формы лейкоцитов, которые могут сигнализировать о гематологических, воспалительных, инфекционных заболеваниях.
Лейкоцитарная формула является одним из самых важных методов лабораторной диагностики практически всех заболеваний. Любые изменения в периферической крови сигнализируют о патологических/физиологических переменах в организме.
Принцип Бабине
Вы будете перенаправлены на Автор24
Принцип или теорема Бабине является следствием гипотезы Френеля. Он связывает дифракционные поля для некоторого экрана с полями для дополнительного экрана.
Описанные выше экраны называют дополнительными если:
Например, подобными экранами могут быть два непрозрачных экрана, имеющие отверстия. Отверстия одного экрана не совпадают с отверстиями другого. Или говорят, что отверстия одного экрана совпадают с непрозрачными частями другого экрана. Так, дополнительным экраном называют экран, который получают заменой отверстий на экран, а экрана на отверстия.
Сложим выражения (4), учитывая (3), имеем:
Применение принципа Бабине к случаю дифракции Фраунгофера
Допустим, что мы наблюдаем фраунгоферовскую дифракционную картину в фокальной плоскости линзы. Если на пути параллельных лучей нет препятствия, то световое поле в данной плоскости везде равно нулю за исключением фокуса линзы. Так, в соответствии с формулой (6) в любой точке фокальной плоскости за исключением фокуса мы имеем:
Готовые работы на аналогичную тему
Для наблюдения доступна интенсивность поля света, а не его фаза, получаем, что фраунгоферовы дифракционные картины от дополнительных экранов, которые получаются в фокальной плоскости линзы, везде одинаковы, исключение составляет фокус.
Принцип Бабине выполняется не точно, в некотором приближении, но нарушение считают существенным только около границ диафрагм.
Задание: Покажите, что количество энергии рассеяния равно энергии, которая поглощается черным экраном, если на него падает плоская волна света. В результате дифракции за экраном вместе с неотклонённой волной возникает рассеянный свет. Считайте, что размеры экрана велики в сравнении с длиной волны.
Решение:
В соответствии с законами геометрической оптики при освещении черного экрана светом за ним должна образоваться область геометрической тени, площадь этой тени должна быть равна площади экрана в направлении перпендикулярном к направлению падения света. Однако существование явления дифракции ведет к частичному отклонению света от первоначального направления распространения. Так, на большом расстоянии, позади экрана тень отсутствует. Вместе со светом, который распространялся в начальном направлении, присутствует некоторое количество света под малыми углами к первоначальному направлению (рассеянного света).
Проведем замену исходного экрана дополнительным, то есть отверстием той же величины и формы. В результате такой замены по теореме Бабине интенсивность поля света в бесконечности не изменится во всех направлениях, исключение составит направление первичной волны. Однако следует заметить, что на любое жестко фиксированное направление за отверстием приходит нулевая интенсивность света, так отверстие рассеивает весь свет, который на него падает. С другой стороны, экран по условию поглощает полностью весь падающий на него свет, так как является черным. Получаем, что полное количество рассеянного света на черном теле равно количеству света, которое падает на его поверхность и поглощенного им. Следовательно, мы получили, что требовалось показать.
Решение:
Если источником плоской волны является лазер, размеры пучка излучения много меньше ширины щели, то без препятствий на экране будем иметь яркое световое пятно. В остальной области экрана поле световой волны монжо принять равным нулю. Для этой области (без пятна), можно записать:
Соответственно для интенсивностей:
В области основного пятна имеем:
\[I_
Получаем, что для щели и проволоки, обладающих одинаковыми размерами, распределение интенсивностей на экране одинаково везде, кроме места, где попадает исходный пучок лазера, если препятствия нет. Если толщина проволоки равна размеру первого максимума дифракции для щели (помним, что их размеры одинаковы), то для обоих объектов исследования совпадают координаты всех минимумов и максимумов картины дифракции.
При дифракции на проволоке помимо минимумов, которые соответствуют минимумам дифракции на щели, можно увидеть еще два резких минимума в области уменьшения интенсивности лазерного пучка. Это объяснимо при использовании принципа Бабине. Так, в области пучка лазера выполняется соотношение:
Данная точка ($
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 18 03 2021
Принцип Бабине
Принцип (теорема) Бабине
Принцип (теорема) Бабине о свойствах дополнительных экранов является следствием гипотезы Френеля.
Выше названные экраны называют дополнительными, если выполняется условие:
Примером дополнительных экранов могут служить два экрана, имеющих отверстия, если отверстия на одном экране совпадают с непрозрачными участками второго экрана.
При суммировании выражений (3) и (4) получаем:
Выражение (6) принцип Бабине в скалярном виде.
Рассмотри дифракцию Фраунгофера. Пусть на пути распространения параллельных лучей отсутствуют любые препятствия, тогда световое поле в фокальной плоскости линзы будет равно нулю всюду, за исключением фокуса. В таком случае по теореме Бабине (6) мы получим в каждой точке рассматриваемой плоскости (не в фокусе линзы) равенство:
Равенство (8) означает, что картины дифракции при рассматриваемом явлении в фокальной плоскости линзы всюду одинаковые, исключением является фокус.
Теорема Бабине не является строгим утверждением, но ее нарушения являются существенными только у границ, рядом с которыми происходит дифракция. Представленная формулировка теоремы не всегда является удовлетворительной, так как она относится к скалярным полям и основана на приближении Кирхгофа.
Примеры задач с решением
Решение. Следуя условиям задачи и согласно принципу Бабине можно записать следующие соотношения между полями, приведенными в условиях:
Данные соотношения являются векторным аналогом скалярного принципа Бабине. Для плоской волны, которая падает на дифракционный экран, получаем, что в направлениях, которые не совпадают с направлениями падения волны, интенсивности поля дифракции для экрана и его дополнений одинаковы. При этом сами поля связывают соотношения:
Задание. Приведите пример, в котором следует использовать строгую векторную формулировку принципа Бабине.