Фрактал мальденброта что это

Почему множество Мандельброта устроено так, как оно устроено

О чём вообще речь

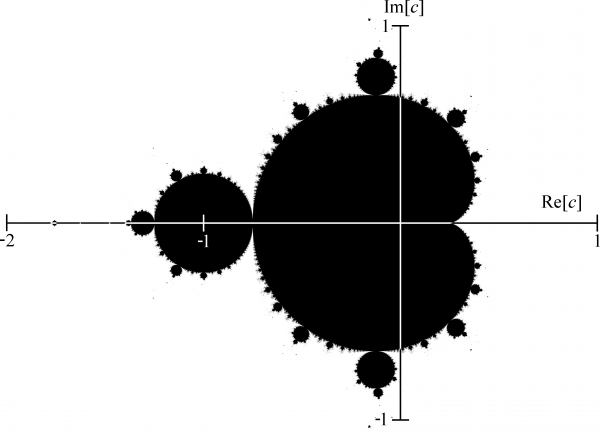
Множество Мандельбро́та — это «множество таких точек C на комплексной плоскости, для которых рекуррентное соотношение при задаёт ограниченную последовательность» (вики).

Иными словами, на каждом шаге число возводится в квадрат и к нему добавляется константа. Начальное значение всегда (0, 0i), варьируется именно константа. Если за определенное число шагов последовательность осталась в заданных пределах, то значение константы принадлежит множеству. Выглядит это так:

Фиг.1 Множество Мандельброта в координатах — реальная и мнимая части константы. Отсюда.

Чаще действуют по другому — фиксируют радиус и для каждого значения константы подсчитывают число итераций, за которое последовательность до него добралась. Это позволяет раскрасить пограничные области множества, не принадлежащие, впрочем, самому множеству.

Фиг.2 Типичная цветовая схема

И откуда же всё это берется?

Нельзя просто так вот взять и ответить на этот вопрос.

Начнём с малого, изучим простую казалось бы операцию — возведение в квадрат.

Основа,

Итак, что же это за возведение в квадрат комплексного числа, ведь именно оно лежит в основе наблюдаемой магии?

Комплексные числа будем рассматривать как двумерный вектор из реальной и мнимой части (что бы это ни означало) либо в полярных координатах как пару длина — угол.

Формула Муавра утверждает, что возведение комплексного числа в квадрат приводит к возведению длины в квадрат, угол при этом удваивается.

Фиг.3 Стартуем с угла 0.001 рад

Вот первые 12 итераций возведения в квадрат комплексного числа с длиной 1 и углом — 0.001 рад, где угол отсчитывается от действительной единицы против часовой стрелки. Когда угол превышает 2π, используется остаток от деления. Отрицательные углы тоже в деле.

Какие особенности есть у последовательности ?

Фиг.4 Последовательности для начальных углов в π/3, π/5, π/7, π/11

Забавно, циклы для π/n образуются по углам правильного n-угольника с одним из углов в стационарной точке (1,0i), но этот угол не посещается. Это проистекает из того, что, например, () не может породить 0, а только лишь числа от 1 до 12.

Но это всё простые делители. Попробуем что-нибудь непростое и нечётное.

Фиг.5 Последовательности для начальных углов в π/9, π/15, π/21.

Фиг.6 Последовательность с началом в 0.001 рад

Здесь показаны первые 500 и 5000 точек из уже знакомой последовательности, начинающейся с угла 0.001 радиана.

Отлично видно проявившуюся кардиоидо-подобную структуру. Происхождение её очевидно, если поделить единичный круг на 8 секторов

Фиг.7 Сектора

то в силу удвоения угла,
точки из сектора 1 могут попасть только в сектор 2 (или остаться в 1)
точки из сектора 2 могут попасть в сектора 3 и 4
точки из сектора 3 могут попасть в сектора 5 и 6
точки из сектора 4 могут попасть в сектора 7 и 8

К слову сказать, чтобы получить последовательность из 5000 адекватных значений, пришлось работать с точностью до 2000 значащих цифр. Фактически, каждая итерация последовательности приводит (грубо, за счет использования остатка от деления угла) к потере одного старшего разряда и подтягиванию одного разряда снизу, из “великого ничто”. Понятно, в “великом ничто” точность неограниченна, нам же приходится работать с конечными объемами данных.

Малые возмущения

Сейчас немного отойдём от чистого в сторону исходной задачи. На каждой итерации станем подмешивать константу. Правда, стартовая точка будет не в начале координат, а на единичной окружности. В результате можно работать с очень маленькими константами, ведь в этом случае не требуется вытаскивать последовательность на окружность для демонстрации нетривиального поведения.

Константа — это просто вектор из начала координат. В зависимости от того, где находится текущая итерация последовательности на единичной окружности, константа действует по-разному. Иные точки она “задувает” внутрь “кратера”, другие “сдувает” наружу. От баланса этих воздействий зависит, удержится ли последовательность в окрестностях единичной окружности или же безвозвратно уйдёт с дистанции.

Начнём со знакомой точки 0.001 радиана.

Фиг.8 Траектории при малых реальных отклонениях от 0.001 рад

Всего 58 итераций потребовалось, чтобы сойти с единичного круга и стремиться в бесконечность в случае константы (0, i*1e-15). При константе (0, i*-1e-15), последовательность ушла в 0 на 62 шагу.

Фиг.9 Окрестность 0 константы для стартовой точки 0.001 рад

Здесь показано, на какой итерации последовательность пересекла круг с радиусом 2 в зависимости от величины комплексной константы. Шаг . Отметим следующее:

Здесь показан старт последовательности с точки с углом 1⅓π, это одна из точек цикла со стартом в π/3. Цикл состоит из двух точек — ⅔ и 1⅓π. Казалось бы, константа должна разнонаправленно действовать на эти точки, нивелируя саму себя. Но нет, никакой интриги и тут не видно. Куда направлен вектор константы по отношению к первой точке последовательности, туда и “сдувает” траекторию.

Пожалуй, на этом мы закончим с ,
в следующий раз займёмся центральной кардиоидой.

Сегодня мы уже встречались с кардиоидой, есть ли между ними связь или просто совпадение?
А может это сигнал «для тех кто понимает»?

Источник

Как устроено множество Мандельброта. Хвост

Хвостом будем считать череду структур к западу от центральной кардиоиды вдоль по отрицательной части вещественной оси. В этой области таится целая бездна деталей. А в деталях, как известно, кроется дьявол … и его малютки.

Данная статья продолжает серию об устройстве множества Мандельброта.

Большой довесок

Так будем называть круг множества Мандельброта с центром в точке (-1, i*0) и радиусом ¼.

Фиг.1 большой довесок

Точка (-1, i*0) забавная, после возведения в квадрат превращается в (1, i*0), после добавления константы становится (0, i*0). На второй итерации возвращается в исходное положение.

Попробуем провернуть тот же трюк, что удался при исследовании центральной кардиоиды — посмотрим куда сходятся траектории, начинающиеся с приграничных точек.

Фиг.2 финальные точки траекторий, стартующих с периметра “большого довеска”

starting circle — круг с центром в (-1, 0 i) и радиусом 0.2495. Честный радиус — 0.25, но точки с него сходятся крайне медленно.

final — по две точки на каждую стартовую. Обладают центральной симметрией относительно точки (-0.5, 0 i). Между углами в исходном круге и param разница в .

Показана только половина соединяющих линий. Шаг — полтора градуса.

param — экспериментально полученная параметрическая кривая , сдвинутая на (-0.5, 0 i).

Вообще, кривая param имеет четыре лепестка — два в вещественной области и два в мнимой. Это звучит странно т.к. мы уже находимся в комплексной плоскости.

Для начала проверим что две чисто вещественные точки переходят друг в друга.
Возьмём минимальную точку (-1¼, 0 i)

В этой области отрицателен. Пусть .

Тогда param:.

Фактически, мнимые лепестки развернулись и легли поверх действительных.

Если бы не это, пришлось бы ломать голову, почему при мы попадаем на вещественные лепестки, а при нет.

Есть всё же в этом какая-то натяжка. Осталось ощущение очень мелкой возни и упущенной общей картины. Но по крайней мере теперь у нас в наличии есть оба элементарных блока из которых построено всё множество — круг и кардиоида. Осталось научиться смешивать их в нужных пропорциях.

Малые довески

А что происходит в интервале [-2:-1.25]?

Пройдёмся по этому отрезку и нарисуем предельные траектории, полученные с точек на нём. Поскольку мнимая часть на этом отрезке (для всех точек траектории) отсутствует, получается вполне наглядное представление — стартовая точка против финальных траекторных.

Финальными траекторными будем считать точки, полученные с помощью следующей эвристики.

Здесь для наглядности приведена часть множества Мандельброта в том же масштабе, соответствующая рассматриваемому отрезку.

Имеем дело с бифуркационной диаграммой для последовательности .

Фиг.4 фрагмент бифуркационной ддиаграммы

Каждый раз, когда мы видим на диаграмме “прогалину”, ей соответствует не просто окружность, а миниатюрная копия множества Мандельброта, со своей кардиоидой, большим и малыми довесками…

Фиг.5 фрагмент множества Мандельброта,
центр (-1,4171. 0), длина стороны 0.002668…

Как такое возможно?

Что объединяет все такие структуры?

Чем они отличаются от “довесков”?

Здесь наглядности, стоит привести бифуркационный “спектр” — зависимость длины предельного цикла от константы. Спектр получен с помощью эвристики и имеет значение только для оценки общей картины.

Фиг.6 бифуркационный спектр c шагом в 0.001

Фиг.7 спектр с разными шагами

Чем меньше шаг, тем больше выявляется циклов разной длины. Обратим внимание на характерные “лесенки” — удвоения периодов не только в изначальном каскаде бифуркаций, но и во всех “прогалинах/окнах периодичности”. Глядя на них невозможно не упомянуть теорему Шарковского

Фиг.8 порядок Шарковского

Оператор x y означает, что если существует цикл длины x, обязан быть и цикл длины y. Нижняя строка соответствует начальному каскаду бифуркаций.

Лесенки у окон периодичности — столбцам вплоть до последней строки. С первой строкой, похоже, придётся повозиться.

Но вернёмся к бифуркационной диаграмме.

Вцелом картина неясна, поэтому зацепимся за что-нибудь, поддающееся осмыслению, потянем за эту ниточку и потихоньку распустим весь клубок.

Удачный кандидат быть такой ниточкой — самое большое окно за “горизонтом событий” — [-1.7684:-1.75] с длиной цикла 3. Взглянем поближе на все три непустых фрагмента этого окна.

Фиг.9 Центральная часть большого окна.

Фиг.10 Верхняя часть

Фиг.11 Нижняя часть

Фиг.12 Наложение полинома на бифуркационную диаграмму

Фиг.14 Фазовая диаграмма траекторий циклов длины

3, по X — предыдущее значение, по Y — текущее.

‘pp3center’ — проходит через 0
‘pp3start’ — максимальное значение диапазона, тоже длины 3,
‘pp3fin’ — за пределами диапазона цикл расщепился до длины 24.
Движение везде по часовой стрелке.

Лирическое отступление. Есть такое устойчивое выражение “period three implies chaos” (в порядке Шарковского всё начинается именно с трёх), то что мы наблюдаем проливает свет, почему именно 3.

В самом деле, из этих трёх два являются “обязательной программой” — 0 и начальное значение константы. Любое наблюдаемое окно периодичности содержит (центральную, основную, базовую?) траекторию, проходящую через 0. Почему, это отдельный вопрос, постараемся ответить на него позже. Но где есть 0, на траектории будет и начальная константа. А без этой парочки 3 превращается в 1, меньше которой уже и нет ничего. Т.е. есть циклы длины 1 и 2, которые мы видели и до “горизонта событий” в регулярной части бифуркационной диаграммы. Причем, цикл длины 2 сам является “обязательной программой”, а длины 1 — ещё и вырожденной оной.

А как насчет циклов большей длины? Судя по бифуркационной диаграмме с наложенными модами, если требуется найти цикл длины n, стоит поискать 0 для функции . Это довольно просто проверить, для этого

Фиг.15 возможный фрактал, соответствующий одному из корней моды

Надо еще кстати умудриться попасть в нужный фрактал, там ими всё буквально испещрено. Ведь мод бесчисленное количество и у каждой есть корни, число которых растёт по экспоненте с ростом номера моды. К счастью, размер фракталов при этом уменьшается.

И всё же, как это работает, почему когда мода пересекает 0, появляются фрактальные структуры?

Стартовые константы получены вышеописанным образом из gnuplot.

Фиг.16 Фазовая диаграмма траекторий циклов длины 4, в названии стартовая константа
‘pp4-1,3107’ получен двойной бифуркацией и находится до ‘горизонта событий’.
‘pp4-1.9408’ обход по часовой стрелке

Фиг.17 Фазовая диаграмма траекторий циклов длины 5
Забавно, ‘pp5-1.98542’ получается из ‘pp4-1.9408’ изломом одной грани.

Фиг.18 Фазовая диаграмма траекторий циклов длины 6
‘pp6-1.77289’ получен расщеплением цикла длины 3.
‘pp6-1.99638’ получен дальнейшим изломом грани в ‘pp5-1.99638’
‘pp6-1.75488’ порождает цикл длины 3 т.к. попадает в окно с периодичностью 3, которое имеет приоритет.

Далее мы не будем смотреть на все имеющиеся циклы, с ростом периода число корней моды растёт экспоненциально, да и степени в полиномах возникают такие, что как-то становится тревожно за точность gnuplot. Просто поглядим на субъективно интересное.

Фиг.19 само-непересекающиеся циклы длины 3. 7

Эти циклы разного размера, но имеют близкую родственную связь. Заключается она в том, что всё это циклы с минимальным корнем соответствующей моды.

Аналогичный цикл длины больше 7 отловить не удалось из-за нарастающей потери точности в вычислениях.

Фиг.20 Еще одна серия траекторий с ростом длины циклов по единице.
Это, кстати, вторые снизу минимальные корни.
По-видимому, это (+1) вполне популярная история. Возможно, стоит продолжить.

Фиг.21 Третьи снизу корни мод.

В принципе логика понятна.

Фиг.22 Фазовая диаграмма траектории длины 11.

Здесь хорошо видно, как нарастает число “зубьев”, а также то, что точки фазовой диаграммы находятся на параболе, что логично, учитывая их происхождение.

Однако, и это еще не всё. Встречаются и вот такие жемчужины:

Фиг.23 цикл длины 9 — утроение цикла.

До сих пор мы встречали только удвоение циклов, например, “pp6-1.77289” из “pp3-1.755”.

Фиг.24 удвоение и утроение цикла 3.

Фиг.25 Бифуркационный “спектр” в интересующем нас интервале.

Невозможно не отметить, насколько этот кусочек спектра похож на полный спектр, приведенный выше (Фиг.7). Что еще раз указывает на фрактальную природу происходящего.

Фиг.26 Расщепление цикла 3 на 4, 5, 6 частей

И до кучи, вот так выглядит попадание мимо окна периодичности (если вообще можно попасть мимо окна периодичности), либо очень большой цикл, что в общем то одно и то же.

Фиг.27 псевдо-хаотическое поведение, длинный цикл.

Подводя итоги, нельзя не отметить что данная статья поднимает больше вопросов, чем даёт ответов.

Чем всё же определяется форма и размер больших и малых довесков?

Как связаны между собой моды?

Неужели мы забыли, что у полиномов есть не только вещественные корни?

Не торчат ли здесь уши сферических функций?

Источник

Загадочный беспорядок: история фракталов и области их применения

Одно из таких «незаметных» открытий — фракталы. Вам наверняка доводилось слышать это запоминающееся слово, но знаете ли вы, что оно означает и как много интересного скрыто в этом термине?

В каждом человеке заложена природная любознательность, стремление познавать окружающий его мир. И в этом стремлении человек старается придерживаться логики в суждениях. Анализируя процессы, происходящие вокруг него, он пытается найти логичность происходящего и вывести некоторую закономерность. Самые большие умы на планете заняты этой задачей. Грубо говоря, ученые ищут закономерность там, где ее быть не должно. Тем не менее даже в хаосе можно найти связь между событиями. И эта связь — фрактал.

Наша маленькая дочь, четырех с половиной лет, сейчас находится в том прекрасном возрасте, когда число вопросов «Почему?» многократно превышает число ответов, которые взрослые успевают давать. Не так давно, рассматривая поднятую с земли ветку, дочка вдруг заметила, что эта ветка, с сучками и ответвлениями, сама похожа на дерево. И, конечно, дальше последовал привычный вопрос «Почему?», на который родителям пришлось искать простое объяснение, понятное ребенку.

Обнаруженная ребенком схожесть отдельной веточки с целым деревом — это очень точное наблюдение, которое лишний раз свидетельствует о принципе рекурсивного самоподобия в природе. Очень многие органические и неорганические формы в природе формируются аналогично. Облака, морские раковины, «домик» улитки, кора и крона деревьев, кровеносная система и так далее — случайные формы всех этих объектов могут быть описаны фрактальным алгоритмом.

⇡#Бенуа Мандельброт: отец фрактальной геометрии

Само слово «фрактал» появилось благодаря гениальному ученому Бенуа Мандельброту (Benoît B. Mandelbrot).

Он сам придумал этот термин в семидесятых годах прошлого века, позаимствовав слово fractus из латыни, где оно буквально означает «ломанный» или «дробленный». Что же это такое? Сегодня под словом «фрактал» чаще всего принято подразумевать графическое изображение структуры, которая в более крупном масштабе подобна сама себе.

Математическая база для появления теории фракталов была заложена за много лет до рождения Бенуа Мандельброта, однако развиться она смогла лишь с появлением вычислительных устройств. В начале своей научной деятельности Бенуа работал в исследовательском центре компании IBM. В то время сотрудники центра трудились над передачей данных на расстояние. В ходе исследований ученые столкнулись с проблемой больших потерь, возникающих из-за шумовых помех. Перед Бенуа стояла сложная и очень важная задача — понять, как предсказать возникновение шумовых помех в электронных схемах, когда статистический метод оказывается неэффективным.

Просматривая результаты измерений шума, Мандельброт обратил внимание на одну странную закономерность — графики шумов в разном масштабе выглядели одинаково. Идентичная картина наблюдалась независимо от того, был ли это график шумов за один день, неделю или час. Стоило изменить масштаб графика, и картина каждый раз повторялась.

При жизни Бенуа Мандельброт неоднократно говорил, что он не занимается формулами, а просто играет с картинками. Этот человек мыслил очень образно, а любую алгебраическую задачу переводил в область геометрии, где, по его словам, правильный ответ всегда очевиден.

Неудивительно, что именно человек с таким богатым пространственным воображением стал отцом фрактальной геометрии. Ведь осознание сути фракталов приходит именно тогда, когда начинаешь изучать рисунки и вдумываться в смысл странных узоров-завихрений.

Фрактальный рисунок не имеет идентичных элементов, но обладает подобностью в любом масштабе. Построить такое изображение с высокой степенью детализации вручную ранее было просто невозможно, на это требовалось огромное количество вычислений. Например, французский математик Пьер Жозе Луи Фату (Pierre Joseph Louis Fatou) описал это множество более чем за семьдесят лет до открытия Бенуа Мандельбротом. Если же говорить про принципы самоподобия, то о них упоминалось еще в трудах Лейбница и Георга Кантора.

Один из первых рисунков фрактала был графической интерпретацией множества Мандельброта, которое родилось благодаря исследованиям Гастона Мориса Жюлиа (Gaston Maurice Julia).

Гастон Жюлиа (всегда в маске — травма с Первой мировой войны)

Этот французский математик задался вопросом, как будет выглядеть множество, если построить его на основе простой формулы, проитерированной циклом обратной связи. Если объяснить «на пальцах», это означает, что для конкретного числа мы находим по формуле новое значение, после чего подставляем его снова в формулу и получаем еще одно значение. Результат — большая последовательность чисел.

Чтобы получить полное представление о таком множестве, нужно проделать огромное количество вычислений — сотни, тысячи, миллионы. Вручную это сделать было просто нереально. Но когда в распоряжении математиков появились мощные вычислительные устройства, они смогли по-новому взглянуть на формулы и выражения, которые давно вызывали интерес. Мандельброт был первым, кто использовал компьютер для просчета классического фрактала. Обработав последовательность, состоящую из большого количества значений, Бенуа перенес результаты на график. Вот что он получил.

Впоследствии это изображение было раскрашено (например, один из способов окрашивания цветом — по числу итераций) и стало одним из самых популярных изображений, какие только были созданы человеком.

Как гласит древнее изречение, приписываемое Гераклиту Эфесскому, «В одну и ту же реку нельзя войти дважды». Оно как нельзя лучше подходит для трактования геометрии фракталов. Как бы детально мы ни рассматривали фрактальное изображение, мы все время будем видеть схожий рисунок.

Желающие посмотреть, как будет выглядеть изображение пространства Мандельброта при многократном увеличении, могут сделать это, загрузив анимационный GIF.

⇡#Лорен Карпентер: искусство, созданное природой

Теория фракталов скоро нашла практическое применение. Поскольку она тесно связана с визуализацией самоподобных образов, неудивительно, что первыми, кто взял на вооружение алгоритмы и принципы построения необычных форм, были художники.

Будущий сооснователь легендарной студии Pixar Лорен Карпентер (Loren C. Carpenter) в 1967 году начал работать в компании Boeing Computer Services, которая была одним из подразделений известной корпорации, занимающейся разработкой новых самолетов.

В 1977 году он создавал презентации с прототипами летающих моделей. В обязанности Лорена входила разработка изображений проектируемых самолетов. Он должен был создавать картинки новых моделей, показывая будущие самолеты с разных сторон. В какой-то момент в голову будущему основателю Pixar Animation Studios пришла в голову креативная идея использовать в качестве фона изображение гор. Сегодня такую задачу может решить любой школьник, но в конце семидесятых годов прошлого века компьютеры не могли справиться со столь сложными вычислениями — графических редакторов не было, не говоря уже о приложениях для трехмерной графики. В 1978 году Лорен случайно увидел в магазине книгу Бенуа Мандельброта «Фракталы: форма, случайность и размерность». В этой книге его внимание привлекло то, что Бенуа приводил массу примеров фрактальных форм в реальной жизни и доказывал, что их можно описать математическим выражением.

Такая аналогия была выбрана математиком не случайно. Дело в том, что как только он обнародовал свои исследования, ему пришлось столкнуться с целым шквалом критики. Главное, в чем упрекали его коллеги, — бесполезность разрабатываемой теории. «Да, — говорили они, — это красивые картинки, но не более. Практической ценности теория фракталов не имеет». Были также те, кто вообще считал, что фрактальные узоры — просто побочный результат работы «дьявольских машин», которые в конце семидесятых многим казались чем-то слишком сложным и неизученным, чтобы всецело им доверять. Мандельброт пытался найти очевидное применение теории фракталов, но, по большому счету, ему и не нужно было это делать. Последователи Бенуа Мандельброта в следующие 25 лет доказали огромную пользу от подобного «математического курьеза», и Лорен Карпентер был одним из первых, кто опробовал метод фракталов на практике.

Проштудировав книжку, будущий аниматор серьезно изучил принципы фрактальной геометрии и стал искать способ реализовать ее в компьютерной графике. Всего за три дня работы Лорен смог визуализировать реалистичное изображение горной системы на своем компьютере. Иными словами, он с помощью формул нарисовал вполне узнаваемый горный пейзаж.

Принцип, который использовал Лорен для достижения цели, был очень прост. Он состоял в том, чтобы разделять более крупную геометрическую фигуру на мелкие элементы, а те, в свою очередь, делить на аналогичные фигуры меньшего размера.

Используя более крупные треугольники, Карпентер дробил их на четыре мелких и затем повторял эту процедуру снова и снова, пока у него не получался реалистичный горный ландшафт. Таким образом, ему удалось стать первым художником, применившим в компьютерной графике фрактальный алгоритм для построения изображений. Как только стало известно о проделанной работе, энтузиасты по всему миру подхватили эту идею и стали использовать фрактальный алгоритм для имитации реалистичных природных форм.

Одна из первых визуализаций 3D по фрактальному алгоритму

Всего через несколько лет свои наработки Лорен Карпентер смог применить в куда более масштабном проекте. Аниматор создал на их основе двухминутный демонстрационный ролик Vol Libre, который был показан на Siggraph в 1980 году. Это видео потрясло всех, кто его видел, и Лоурен получил приглашение от Lucasfilm.

Анимация рендерилась на компьютере VAX-11/780 от Digital Equipment Corporation с тактовой частотой пять мегагерц, причем прорисовка каждого кадра занимала около получаса.

Работая для Lucasfilm Limited, аниматор создавал по той же схеме трехмерные ландшафты для второго полнометражного фильма саги Star Trek. В фильме «Гнев Хана» (The Wrath of Khan) Карпентер смог создать целую планету, используя тот же самый принцип фрактального моделирования поверхности.

В настоящее время все популярные приложения для создания трехмерных ландшафтов используют аналогичный принцип генерирования природных объектов. Terragen, Bryce, Vue и прочие трехмерные редакторы полагаются на фрактальный алгоритм моделирования поверхностей и текстур.

⇡#Фрактальные антенны: лучше меньше, да лучше

За последние полвека жизнь стремительно стала меняться. Большинство из нас принимает достижения современных технологий как должное. Ко всему, что делает жизнь более комфортной, привыкаешь очень быстро. Редко кто задается вопросами «Откуда это взялось?» и «Как оно работает?». Микроволновая печь разогревает завтрак — ну и прекрасно, смартфон дает возможность поговорить с другим человеком — отлично. Это кажется нам очевидной возможностью.

Но жизнь могла бы быть совершенно иной, если бы человек не искал объяснения происходящим событиям. Взять, например, сотовые телефоны. Помните выдвижные антенны на первых моделях? Они мешали, увеличивали размеры устройства, в конце концов, часто ломались. Полагаем, они навсегда канули в Лету, и отчасти виной тому… фракталы.

Фрактальные рисунки завораживают своими узорами. Они определенно напоминают изображения космических объектов — туманностей, скопления галактик и так далее. Поэтому вполне закономерно, что, когда Мандельброт озвучил свою теорию фракталов, его исследования вызвали повышенный интерес у тех, кто занимался изучением астрономии. Один из таких любителей по имени Натан Коэн (Nathan Cohen) после посещения лекции Бенуа Мандельброта в Будапеште загорелся идеей практического применения полученных знаний. Правда, сделал он это интуитивно, и не последнюю роль в его открытии сыграл случай. Будучи радиолюбителем, Натан стремился создать антенну, обладающую как можно более высокой чувствительностью.

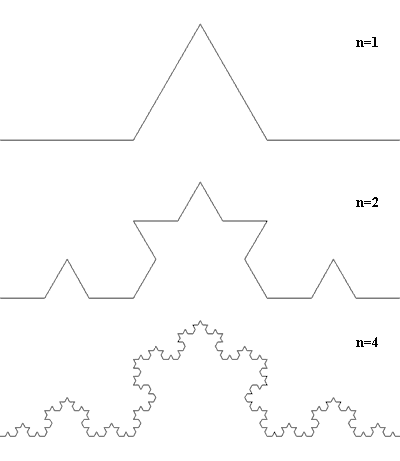
Единственный способ улучшить параметры антенны, который был известен на то время, заключался в увеличении ее геометрических размеров. Однако владелец жилья в центре Бостона, которое арендовал Натан, был категорически против установки больших устройств на крыше. Тогда Натан стал экспериментировать с различными формами антенн, стараясь получить максимальный результат при минимальных размерах. Загоревшись идеей фрактальных форм, Коэн, что называется, наобум сделал из проволоки один из самых известных фракталов — «снежинку Коха». Шведский математик Хельге фон Кох (Helge von Koch) придумал эту кривую еще в 1904 году. Она получается путем деления отрезка на три части и замещения среднего сегмента равносторонним треугольником без стороны, совпадающей с этим сегментом. Определение немного сложное для восприятия, но на рисунке все ясно и просто.

Существуют также другие разновидности «кривой Коха», но примерная форма кривой остается похожей

Когда Натан подключил антенну к радиоприемному устройству, он был очень удивлен — чувствительность резко увеличилась. После серии экспериментов будущий профессор Бостонского университета понял, что антенна, сделанная по фрактальному рисунку, имеет высокий КПД и покрывает гораздо более широкий частотный диапазон по сравнению с классическими решениями. Кроме того, форма антенны в виде кривой фрактала позволяет существенно уменьшить геометрические размеры. Натан Коэн даже вывел теорему, доказывающую, что для создания широкополосной антенны достаточно придать ей форму самоподобной фрактальной кривой.

Автор запатентовал свое открытие и основал фирму по разработке и проектированию фрактальных антенн Fractal Antenna Systems, справедливо полагая, что в будущем благодаря его открытию сотовые телефоны смогут избавиться от громоздких антенн и станут более компактными.

В принципе, так и произошло. Правда, и по сей день Натан ведет судебную тяжбу с крупными корпорациями, которые незаконно используют его открытие для производства компактных устройств связи. Некоторые известные производители мобильных устройств, как, например, Motorola, уже пришли к мирному соглашению с изобретателем фрактальной антенны.

⇡#Фрактальные измерения: умом не понять

В своей книге Мандельброт рассказывает об одном очень интересном математическом парадоксе. Пятая глава книги «Фрактальная геометрия природы» посвящена, на первый взгляд, довольно простому вопросу: «Какова длина береговой линии Британии?» (аналогичная статья была опубликована им в журнале Science от 1967 года).

Этот вопрос Бенуа позаимствовал у знаменитого американского ученого Эдварда Каснера.

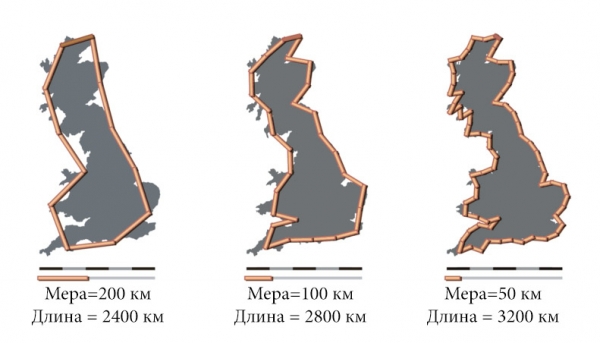
Последний, как и многие другие известные математики, очень любил общаться с детьми, задавая им вопросы и получая неожиданные ответы. Иногда это приводило к удивительным последствиям. Так, например, девятилетний племянник Эдварда Каснера придумал хорошо всем известное теперь слово «гугол», обозначающее единицу со ста нулями. Но вернемся к фракталам. Американский математик любил задавать вопрос, какова длина береговой линии США. Выслушав мнение собеседника, Эдвард сам говорил правильный ответ. Если измерять длину по карте ломаными отрезками, то результат окажется неточным, ведь береговая линия имеет большое количество неровностей. А что будет, если измерять максимально точно? Придется учитывать длину каждой неровности — нужно будет измерять каждый мыс, каждую бухту, скалу, длину скалистого уступа, камня на ней, песчинки, атома и так далее. Поскольку число неровностей стремится к бесконечности, измеренная длина береговой линии будет при измерении каждой новой неровности увеличиваться до бесконечности.

Чем меньше мера при измерении, тем больше измеряемая длина

Интересно, что, следуя подсказкам Эдварда, дети намного быстрее взрослых говорили правильное решение, в то время как у последних были проблемы с принятием такого невероятного ответа.

На примере этой задачи Мандельброт предложил использовать новый подход к измерениям. Поскольку береговая линия близка к фрактальной кривой, значит, к ней можно применить характеризующий параметр — так называемую фрактальную размерность.

Что такое обычная размерность — понятно любому. Если размерность равна единице, мы получаем прямую, если два — плоскую фигуру, три — объем. Однако такое понимание размерности в математике не срабатывает с фрактальными кривыми, где этот параметр имеет дробное значение. Фрактальную размерность в математике можно условно рассматривать как «неровность». Чем выше неровность кривой, тем больше ее фрактальная размерность. Кривая, обладающая, по Мандельброту, фрактальной размерностью выше ее топологической размерности, имеет аппроксимированную протяженность, которая не зависит от количества измерений.

В настоящее время ученые находят все больше и больше областей для применения теории фракталов. С помощью фракталов можно анализировать колебания котировок на бирже, исследовать всевозможные естественные процессы, как, например, колебание численности видов, или моделировать динамику потоков. Фрактальные алгоритмы могут быть использованы для сжатия данных, например для компрессии изображений. И кстати, чтобы получить на экране своего компьютера красивый фрактал, не обязательно иметь докторскую степень.

⇡#Фрактал в браузере

Пожалуй, один из самых простых способов получить фрактальный узор — воспользоваться онлайновым векторным редактором от молодого талантливого программиста Toby Schachman. В основе инструментария этого простого графического редактора лежит все тот же принцип самоподобия.

В вашем распоряжении имеется всего две простейших формы — четырехугольник и круг. Вы можете добавлять их на холст, масштабировать (чтобы масштабировать вдоль одной из осей, удерживайте клавишу Shift) и вращать. Перекрываясь по принципу булевых операций сложения, эти простейшие элементы образуют новые, менее тривиальные формы. Далее эти новые формы можно добавлять в проект, а программа будет повторять генерирование этих изображений до бесконечности. На любом этапе работы над фракталом можно возвращаться к любой составляющей сложной формы и редактировать ее положение и геометрию. Увлекательное занятие, особенно если учесть, что единственный инструмент, который вам нужен для творчества, — браузер. Если вам будет непонятен принцип работы с этим рекурсивным векторным редактором, советуем вам посмотреть видео на официальном сайте проекта, на котором подробно показывается весь процесс создания фрактала.

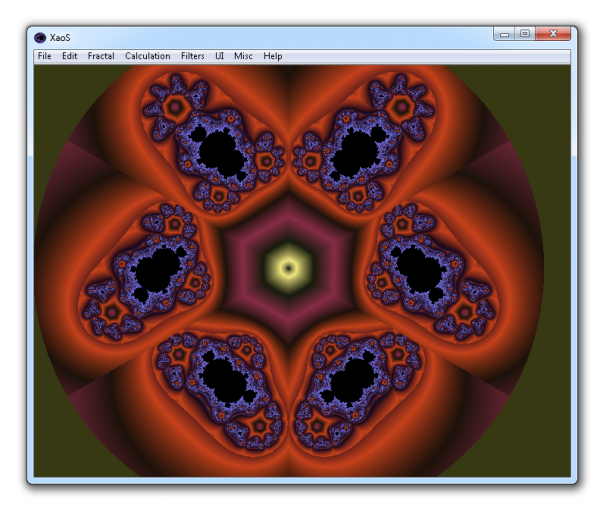
⇡#XaoS: фракталы на любой вкус

Многие графические редакторы имеют встроенные средства для создания фрактальных узоров. Однако эти инструменты обычно являются второстепенными и не позволяют выполнить тонкую настройку генерируемого фрактального узора. В тех случаях, когда необходимо построить математически точный фрактал, на помощь придет кроссплатформенный редактор XaoS. Эта программа дает возможность не только строить самоподобное изображение, но и выполнять с ним различные манипуляции. Например, в режиме реального времени вы можете совершить «прогулку» по фракталу, изменив его масштаб. Анимированное движение вдоль фрактала можно сохранить в виде файла XAF и затем воспроизвести в самой программе.

XaoS может загружать случайный набор параметров, а также использовать различные фильтры постобработки изображения — добавлять эффект смазанного движения, сглаживать резкие переходы между точками фрактала, имитировать 3D-картинку и так далее.

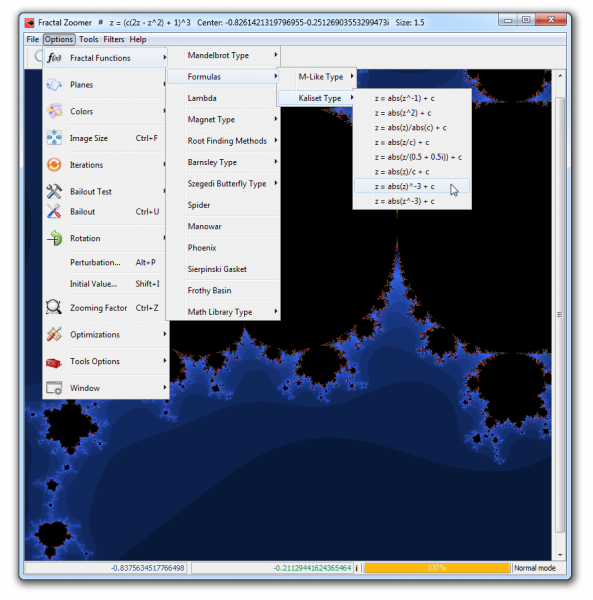
⇡#Fractal Zoomer: компактный фрактальный генератор

По сравнению с другими генераторами изображений фракталов Fractal Zoomer имеет несколько преимуществ. Во-первых, он совсем небольшой по размеру и не требует установки. Во-вторых, в нем реализована возможность определять цветовую палитру рисунка. Вы можете выбирать оттенки в цветовых моделях RGB, CMYK, HVS и HSL.

Также очень удобно использовать опцию случайного подбора цветовых оттенков и функцию инвертирования всех цветов на картинке. Для настройки цвета имеется функция цикличного перебора оттенков — при включении соответствующего режима программа анимирует изображение, циклично меняя на нем цвета.

Fractal Zoomer может визуализировать 85 различных фрактальных функций, причем в меню программы наглядно показываются формулы. Фильтры для постобработки изображения в программе имеются, хотя и в небольшом количестве. Каждый назначенный фильтр можно в любой момент отменить.

⇡#Mandelbulb3D: редактор трехмерных фракталов

Когда употребляется термин «фрактал», чаще всего подразумевается плоское двухмерное изображение. Однако фрактальная геометрия выходит за рамки 2D-измерения. В природе можно найти как примеры плоских фрактальных форм, скажем, геометрию молнии, так и трехмерные объемные фигуры. Фрактальные поверхности могут быть трехмерными, и одна из очень наглядных иллюстраций 3D-фракталов в повседневной жизни — кочан капусты. Наверное, лучше всего фракталы можно разглядеть в сорте романеско — гибриде цветной капусты и брокколи.

А еще этот фрактал можно съесть

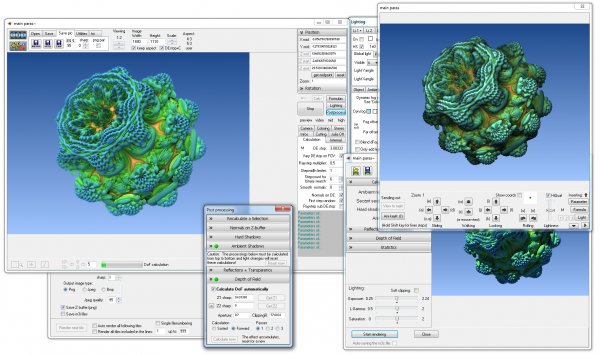
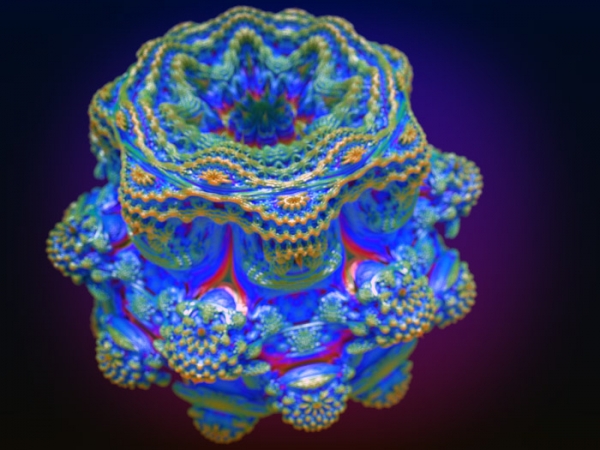
Создавать трехмерные объекты с похожей формой умеет программа Mandelbulb3D. Чтобы получить трехмерную поверхность с использованием фрактального алгоритма, авторы данного приложения, Дениэл Уайт (Daniel White) и Пол Ниландер (Paul Nylander), преобразовали множество Мандельброта в сферические координаты. Созданная ими программа Mandelbulb3D представляет собой самый настоящий трехмерный редактор, который моделирует фрактальные поверхности разных форм. Поскольку в природе мы часто наблюдаем фрактальные узоры, то искусственно созданный фрактальный трехмерный объект кажется невероятно реалистичным и даже «живым».

Он может походить на растение, может напоминать странное животное, планету или что-нибудь другое. Этот эффект усиливается благодаря продвинутому алгоритму визуализации, который дает возможность получать реалистичные отражения, просчитывать прозрачность и тени, имитировать эффект глубины резкости и так далее. В Mandelbulb3D имеется огромное количество настроек и параметров визуализации. Можно управлять оттенками источников света, выбирать фон и уровень детализации моделируемого объекта.

Фрактальный редактор позволяет создавать анимацию. Вы не только конфигурируете трехмерное множество Мандельброта, но и можете его вращать, масштабировать и менять параметры с течением времени.

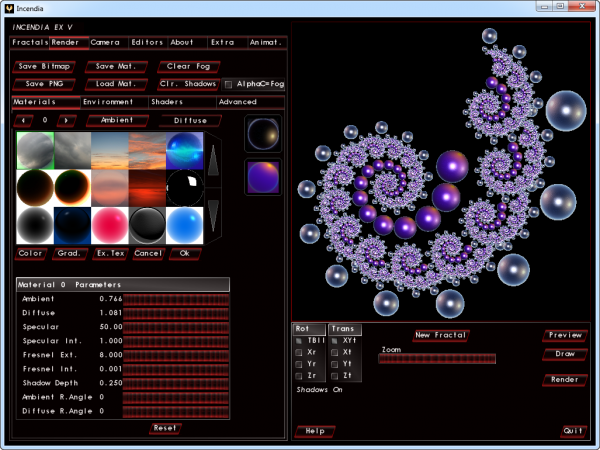
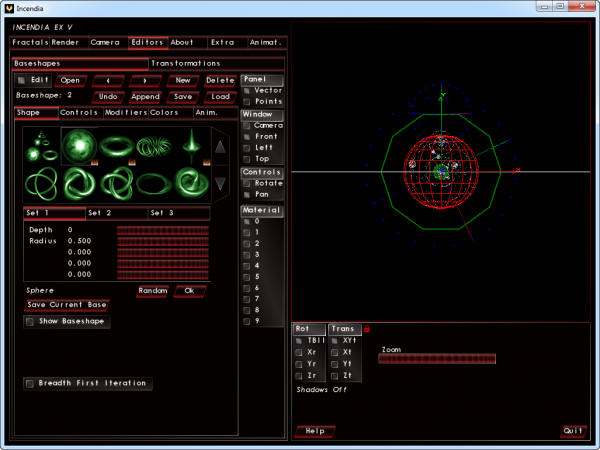
⇡#Генератор трехмерных фракталов Incendia

Incendia — это мультипроцессорный генератор трехмерных фракталов, разработанный испанским программистом Ramiro Perez, который изучает фракталы с 1989 года.

Фрактальный редактор Incendia поддерживает двойное сглаживание изображения, содержит библиотеку из полусотни различных трехмерных фракталов и имеет отдельный модуль для редактирования базовых форм.

Приложение использует фрактальный скриптинг, с помощью которого можно самостоятельно описывать новые типы фрактальных конструкций. В Incendia есть редакторы текстур и материалов, а движок визуализации позволяет использовать эффекты объемного тумана и различные шейдеры. В программе реализована опция сохранения буфера при длительном рендеринге, поддерживается создание анимации.

Incendia позволяет экспортировать фрактальную модель в популярные форматы трехмерной графики — OBJ и STL. В состав Incendia включена небольшая утилита Geometrica — специальный инструмент для настройки экспорта фрактальной поверхности в трехмерную модель. С помощью этой утилиты можно определять разрешение 3D-поверхности, указывать число фрактальных итераций. Экспортированные модели могут быть использованы в 3D-проектах при работе с такими трехмерными редакторами, как Blender, 3ds max и прочие.

В последнее время работа над проектом Incendia несколько затормозилась. На данный момент автор ищет спонсоров, которые помогли бы ему развивать программу.

Если вам не хватает фантазии нарисовать в этой программе красивый трехмерный фрактал — не беда. Воспользуйтесь библиотекой параметров, которая находится в папке INCENDIA_EX\parameters. С помощью файлов PAR вы сможете быстро найти самые необычные фрактальные формы, в том числе и анимированные.

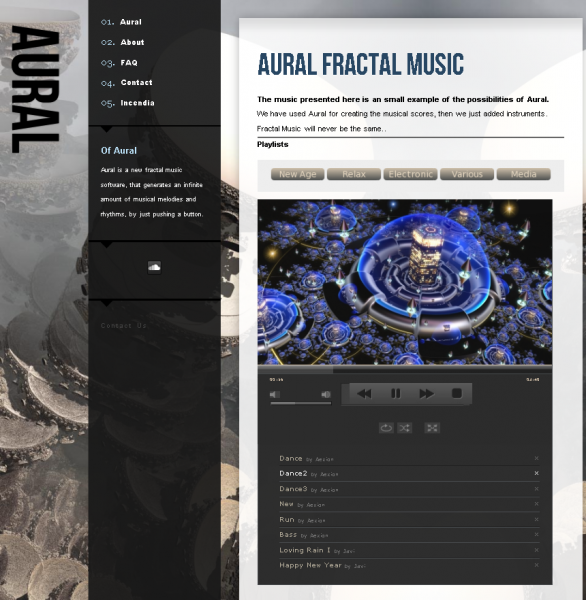
⇡#Aural: как поют фракталы

Мы обычно не рассказываем о проектах, работа над которыми только ведется, однако в данном случае мы должны сделать исключение, уж очень это необычное приложение. Проект под названием Aural придумал тот же человек, что и Incendia. Правда, на этот раз программа не визуализирует фрактальное множество, а озвучивает его, превращая в электронную музыку. Идея очень любопытная, особенно если учесть необычные свойства фракталов. Aural — это аудиоредактор, генерирующий мелодии с использованием фрактальных алгоритмов, то есть, по сути, это звуковой синтезатор-секвенсор.

Последовательность звуков, выдаваемая этой программой, необычна и… красива. Она вполне может пригодиться для написания современных ритмов и, как нам кажется, особенно хорошо подходит для создания звуковых дорожек к заставкам телевизионных и радиопередач, а также «петель» фоновой музыки к компьютерным играм. Рамиро пока не предоставил демонстрационной версии своей программы, но обещает, что, когда он это сделает, для того, чтобы работать с Aural, не нужно будет изучать теорию фракталов — достаточно просто поиграться с параметрами алгоритма генерирования последовательности нот. Послушать, как звучат фракталы, можно здесь и тут.

Фракталы: музыкальная пауза

Вообще-то фракталы могут помочь написать музыку даже без программного обеспечения. Но это может сделать только тот, кто по-настоящему проникнут идеей природной гармонии и при этом не превратился в несчастного «ботана». Тут есть смысл брать пример с музыканта по имени Джонатан Колтон (Jonathan Coulton), который, помимо всего прочего, пишет композиции для журнала Popular Science. И не в пример другим исполнителям, Колтон все свои произведения публикует под лицензией Creative Commons Attribution-Noncommercial, которая (при использовании в некоммерческих целях) предусматривает свободное копирование, распространение, передачу произведения другим лицам, а также его изменение (создание производных произведения), чтобы приспособить его к своим задачам.

У Джонатана Колтона, конечно же, есть песня про фракталы.

⇡#Заключение

Во всем, что нас окружает, мы часто видим хаос, но на самом деле это не случайность, а идеальная форма, разглядеть которую нам помогают фракталы. Природа — лучший архитектор, идеальный строитель и инженер. Она устроена очень логично, и если где-то мы не видим закономерности, это означает, что ее нужно искать в другом масштабе. Люди все лучше и лучше это понимают, стараясь во многом подражать естественным формам. Инженеры проектируют акустические системы в виде раковины, создают антенны с геометрией снежинок и так далее. Уверены, что фракталы хранят в себе еще немало секретов, и многие из них человеку еще лишь предстоит открыть.

Источник