Фрактальная геометрия что это

ФРАКТАЛЬНАЯ ГЕОМЕТРИЯ – ОБЛАСТИ ПРИМЕНЕНИЯ И ПЕРСПЕКТИВЫ РАЗВИТИЯ

English version

Хорев Игорь Владимирович

(ООО «ProЭксперт»)

Аннотация

В статье рассмотрены концептуальные основы фрактальной геометрии как составной части науки о хаосе, приведены описания технологий использования в инженерной графике. Дан краткий обзор областей применения в различных отраслях науки и техники.

Ключевые слова: теория хаоса, фрактал, фрактальная геометрия, инженерная графика.

Наука о хаосе, имеющая в своей структуре фрактальную геометрию, возникла как совокупность методов решения ряда экономических задач, методов моделирования живых и турбулентных систем, которые стали возможны после появления достаточно мощных компьютеров и другого оборудования, необходимого для математического и функционального анализа нашего мировоззрения.

Фрактальная геометрия, один из инструментов теории хаоса, используется для изучения феноменов, которые являются хаотическими только с точки зрения евклидовой геометрии и линейной математики.

Фрактальная геометрия изучает закономерности, проявляемые в структуре природных объектов, процессов и явлений, обладающих явно выраженной фрагментарностью, изломанностью и искривленностью. Они создают новую геометрию, в которой пространство не цельноразмерное, а дробное, или фрактальное.

Достаточно большое число объектов на поверхности Земли и атмосфере подчиняются степенным законам. Моделированию этих закономерностей и занимается фрактальная геометрия.

Цельноразмерная Евклидова геометрия – это 39 аксиом (по Давиду Гильберту). Новую фрактальную геометрию мы будем описывать дополнительно еще двумя аксиомами – аксиомами многомасштабности и самоподобия.

Фрактальный анализ произвел революцию в характере исследований, ведущихся в несметном количестве различных областей науки: метеорологии, медицине, геологии, экономике, метафизике.

Фрактал(лат. fractus — дроблёный) – сложная геометрическая фигура, обладающая свойством самоподобия, т.е. из всей фигуры можно выделить части, подобные целой фигуре. Примеры самоподобных множеств известны с XIX века. Термин «фрактал» (от лат. fractus – раздробленный) впервые ввел в 1975 году математик исследовательского центра IBM Бенуа Мандельброт.

Фракталы можно разделить на несколько видов:

Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.

Бенуа Мандельброт (один из выдающихся первооткрывателей Хаоса) совершил кардинальный прорыв, который можно кратко представить в виде простой математической формулы:

Z2 + c превращается в «z» в ходе следующего повторения.

Это не статическое уравнение. Подобно самой жизни, это динамическое уравнение, существующее во времени. Когда итерация становится квадратичным процессом, результаты предсказуемы и быстро достигают бесконечности:

Тоже будет верно и для любого не комплексного числа, которое меньше единицы.

Оно быстро становиться бесконечно малым:

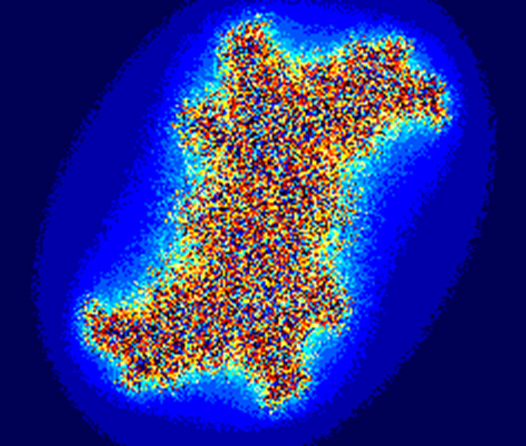
Однако, прибавляя константу » с » (комплексное число ) к квадратичному процессу и полагая первоначально «z» равное нулю, можно получить стабильные итерации, которые не будут приводить ни к бесконечно большим, ни к бесконечно малым числам. Эти числа будут находиться в пределах черной зоны набора Мандельброта. (См. рис.1)

Подобно погоде, фондовый и товарный рынки, а также и другие хаотичные системы, могут порождать непредсказуемые последствия при пренебрежимо малых изменениях в количествах (как в случае с данными о безработице ), помноженных на реакцию на них. Это отражает поведение в четвертом измерении, реальном мире, где Хаос очевиден и является основной структурой большинства упорядоченных систем. Набор Мандельброта, определяющийся формулой, названной в честь ее изобретателя, невозможно было бы создать без использования компьютеров и компьютерной графики. Эта формула является динамическим выражением, основанным на итерации (расчеты базируются на постоянном реагировании) комплексных чисел, началом которых является ноль.

Рассмотрим применение фрактальный алгоритм для моделирования живых систем.

Рекурсивное построение фрактала листа папоротника:

Для построения используется процедура (псевдокод):

Рекомендуемые значения углов и коэффициентов:

Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале (−10∘;10∘) можно получить изображения: (см. изображения 3,4 рис.2 ).

Рассмотрим другое применение фрактальной геометрии – для анализа графиков колебаний цен на биржах.

Следует отметить, основные положения теории хаоса были сформулированы именно на основе анализа поведения цен на рынках. Колебания курсов валют являются одним из наиболее востребованных сфер применения фрактального анализа.

В настоящее время не существует чёткого математического определения фрактала. Применительно к биржевой торговле фрактал определяется как замкнутый промежуток, на котором размещается изменение цены. Фрактал составляется из пяти последовательных баров или свеч. Фрактал всегда означает изменение в поведении; он отражается как последовательность из пяти баров, где центральный бар (или группа) имеет более высокий максимум для фракталов на верх и более низкий минимум фракталов вниз.

На рис. 6 рассматриваются основные виды торговых фракталов.

Один из способов торговли с помощью фрактала состоит в следующем: если рынок преодолевает внешний экстремальный максимум для фрактала наверх или минимум для фрактала вниз, двигайтесь в сторону внешней направленности фрактальной точки.

Кроме того, фракталы позволяют силу толчка цены вверх или вниз. Безусловно, фрактальный анализ не является единственным и достаточным инструментом для успешной торговли, но является ключевым для адекватного понимания сущности рынков.

Сфера применения фрактальной геометрии будет расширятся по мере роста мощности компьютерного оборудования для её визуализации.

Список литературы

Рисунки к докладу

Набор Мандельброта на комплексной плоскости

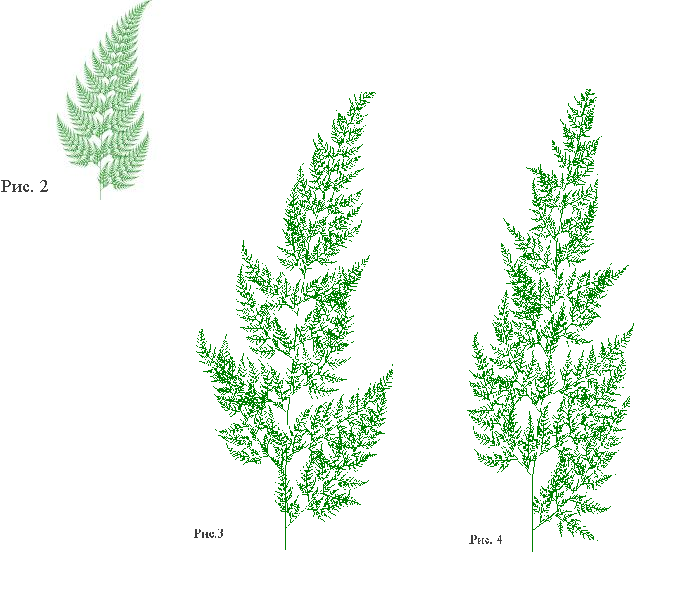
Рис. 2

Рис. 3

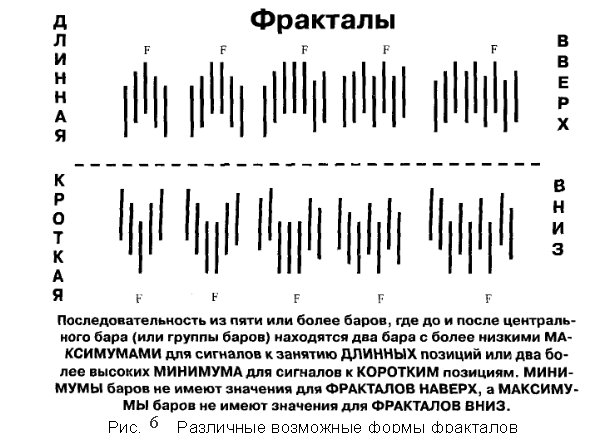
Рис. 4

Основные виды торговых фракталов

Вопросы и комментарии к выступлению:

Здравствуйте Игорь Владимирович, мы коллеги Марии Гавриловны, в конференции есть рубрика «Портреты» и в память о замечательном грамотном преподавателе черчения и геометрии Хоревой Марии Гавриловны можно было было бы дать описание ее биографии, что наверное в полной мере можете воспроизвести только Вы.

Доклад очень интересный и познавательный для всех геометров. Спасибо.

С уважением Шахова А.Б.

Добрый вечер, Игорь Владимирович! Давно ждала начала дискуссии по поводу достижений в области фрактальной геометрии.

С уважением, Л.О.Мокрецова

Дударь Елена Сергеевна
(10 марта 2015 г. 13:10)

Игорь Владимирович, спасибо за интересный доклад!

Для желающих подробнее познакомиться с основами фрактальной геометрии автор любезно предоставил в оргкомитет электронные версии книг: В.К. Балханов «Основы фрактальной геометрии и фрактального исчисления» и монографию Билла Вильямса «Новые измерения в биржевой торговле…».

С позволения автора привожу его отзывы о книгах, в которых в доступной форме изложен «очень сложный материал. Это просто музыкальность в области мысли и логики. Это действительно талантливо и заслуживает внимания».

Источник

LiveInternetLiveInternet

—Рубрики

—Поиск по дневнику

—Подписка по e-mail

—Постоянные читатели

—Сообщества

—Статистика

Понятия фрактал и фрактальная геометрия.

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature’. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.
Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.
Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому».

Классификация фракталов.

Для того, чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации. Существует три класса фракталов.

1. Геометрические фракталы.

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометрический фрактал.

Рассмотрим на примере один из таких фрактальных объектов – триадную кривую Коха.

Построение триадной кривой Коха.

Возьмем прямолинейный отрезок длины 1. Назовем его затравкой. Разобьем затравку на три равные части длиной в 1/3, отбросим среднюю часть и заменим ее ломаной из двух звеньев длиной 1/3.

Для того чтобы перейти к следующему поколению кривой Коха, надо у каждого звена отбросить и заменить среднюю часть. Соответственно длина второго поколения будет 16/9, третьего – 64/27. если продолжить этот процесс до бесконечности, то в результате получится триадная кривая Коха.

Рассмотрим теперь св-ва триадной кривой Коха и выясним, почему же фракталы называли «монстрами».

Во-первых, эта кривая не имеет длины – как мы убедились, с числом поколений ее длина стремится к бесконечности.

Длина и гладкость – фундаментальные св-ва кривых, которые изучаются как евклидовой геометрией, так и геометрией Лобачевского, Римана. К триадной кривой Коха традиционные методы геометрического анализа оказались неприменимы, поэтому кривая Коха оказалась чудовищем – «монстром» среди гладких обитателей традиционных геометрий.

Построение «дракона» Хартера-Хейтуэя.

Для получения другого фрактального объекта нужно изменить правила построения. Пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на этот образующий элемент так, чтобы угол был сверху. Можно сказать, что при такой замене происходит смещение середины звена. При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться. На рисунке представлены несколько первых поколений и 11-е поколение кривой, построенной по вышеописанному принципу. Кривая, при n стремящемуся к бесконечности, называется драконом Хартера-Хейтуэя.
В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов. Двухмерные геометрические фракталы используются для создания объемных текстур (рисунка на поверхности объекта).

2.Алгебраические фракталы

Множество Мандельброта.

3.Стохастические фракталы

О применении фракталов

О построении фракталов

Метод последовательных приближений

Глядя на эту картинку, нетрудно понять, как можно построить самоподобный фрактал (в данном случае пирамиду Серпинского). Нужно взять обычную пирамиду (тетраэдр), затем вырезать ее середину (октаэдр), в результате чего у нас получается четыре маленьких пирамидки. С каждой из них мы проделываем ту же самую операцию и т.д. Это несколько наивное, но наглядное объяснение.

Заметим, что каждая из этих итераций является аттрактором рекуррентной системы итерированных функций (английский термин Digraph IFS, RIFS и также Graph-directed IFS) и поэтому их легко построить с помощью нашей программы.

Построение по точкам или вероятностный метод

Это наиболее лёгкий для реализации на компьютере метод. Для простоты рассмотрим случай плоского самоаффинного множества. Итак, пусть

Источник

Созерцание великого фрактального подобия

(с) «Галактика галактик»

Фракталы — не просто красивое природное явление. Согласно проведенным исследованиям, рассматривание фрактальных структур на 60 % повышает стрессоустойчивость, измеряемую на основе физиологических показателей. При созерцании фракталов в лобной коре головного мозга всего за одну минуту увеличивается активность альфа-волн — как во время медитации или при ощущении легкой сонливости.

Неудивительно, что фрактальный биодизайн оказывает на человека умиротворяющее воздействие. Нам нравится смотреть на облака, на языки пламени в камине, на листву в парке… Как это работает? Ученые предполагают, что естественный ход поисковых движений наших глаз — фрактальный. При совпадении размерности траектории движения глаз и фрактального объекта мы впадаем в состояние физиологического резонанса, за счет чего активизируется деятельность определенных участков мозга.

Но не все фракталы одинаково полезны. В данной статье расскажем о фрактальной размерности и о её влиянии на здоровье.

Биофракталы

(с)

Примеры фракталов в природе встречаются повсеместно: от ракушек до сосновых шишек. Каждый фрактал имеет математическую размерность D. Для человека наиболее полезны фракталы с размерностью 1,3—1,5, и большинство фрактальных объектов, созданных природой, имеют именно такую размерность. А глаз человека эстетически «настроен» на восприятие как раз таких, встречающихся в природе фракталов.

Прекрасным примером фракталов в природе являются деревья. Фракталы можно обнаружить на каждом уровне лесной экосистемы — от семян и сосновых шишек до ветвей и листьев. На иллюстрации выше запечатлена «застенчивая крона» — явление, когда кроны деревьев не соприкасаются, формируя локальные участки лесного полога.

С биологической точки зрения такое расположение крон объясняется естественным отбором — листья расположены как можно дальше друг от друга, чтобы максимизировать доступ к ресурсам, особенно к солнечному свету для фотосинтеза.

Итальянская капуста романеско имеет сверхэффективную конструкцию, позволяющую максимизировать воздействие солнечного света и транспортировать питательные вещества по всей клеточной структуре растения.

Однако размерность этой капусты — 2,66. Вообще, дробная размерность является ключевой особенностью фракталов. При этом большинство из них находится в плоскости между линией (размерность 1) и двухмерной поверхностью (размерность 2). Чем выше показатель, тем больше движение в сторону трехмерных объектов (размерность 3).

Компьютерные игры

Трехмерные фракталы — одни из самых редких в природе. Гораздо проще встретить их в виртуальной реальности. Например, в игре Marble Marcher — уникальной аркаде, где нужно прокатить шар к цели в пространстве, созданном единым всеобъемлющим алгоритмом. Практически все, что вы увидите в игре, создано не дизайнерами, а чистой математикой.

Yedoma Globula — это 3D-песочница на самописном движке, в которой можно исследовать процедурно создаваемые фрактальные ландшафты.

Фрактальные формулы можно использовать в компьютерной графике для создания реалистичных гор, рек, лесов и облаков. Игра Everything пошла гораздо дальше: в ней помимо визуальной составляющей в системообразующей части геймплея использовано фрактальное подобие. Тут фактически нет NPC-персонажей. Вы можете начать игру в образе свиньи, которая бродит по зеленым склонам и встречает дуб, а затем стать дубом, который отправится в самостоятельное путешествие.

Гаджеты

Использовать фракталы как «что-то полезное» можно не только в компьютерных играх или для релаксации. Именно фракталы подсказали способ уменьшения размера антенн для сотовых телефонов. Фрактальная геометрия расширяет способность создавать новые, более практичные устройства.

Сейчас фракталы используются в новом поколении спутниковой связи, в устройствах IoT и других проектах приема, передачи и преобразования радиоволн.

Архитектура

Фракталы можно использовать даже неосознанно. На фото выше изображен фрагмент купола иранской мечети. А здесь вы найдете множество фотографий потолков школ, культурных и религиозных сооружений в Иране, которые демонстрируют невероятно сложные фрактальные рельефы и мозаики, декорирующие изысканные архитектурные элементы.

Храм Деви Джагадамби в Кхаджурахо — отличный пример фрактальной архитектуры. Индийские и многие другие храмы Юго-Восточной Азии имеют фрактальную структуру: главная башня окружена башнями меньшего размера, те в свою очередь — еще более маленькими башнями. И так до восьми (а порой и больше) уровней, представляющих различные аспекты индуистского мифологического пантеона.

Фракталы в архитектуре — не уникальное изобретение одной части света. Сложное убранство готической, ренессансной и барочной архитектуры, особенно выраженное в соборах, часто демонстрирует фрактальное копирование и масштабирование на нескольких уровнях. Характерное для европейской архитектуры с конца XII в. переплетение арок скорее имело не эстетическое, а практическое значение: оно было разработано для укрепления окон и стен против давления ветра.

С конца XX века фрактальную геометрию использовали осознанно для создания интересных и приятных глазу фасадов. На фото — здание одного из самых сложных в архитектурном плане комплексов, расположенное в мельбурнском городском районе (Австралия). В комплексе объединены культурные, рекреационные и коммерческие проекты.

Опасные фракталы

Большинство фрактальных изображений, генерируемых математическими, естественными и человеческими процессами, обладают общим эстетическим качеством, основанным на визуальной сложности. Участники тестов визуального восприятия предпочитают фракталы именно естественного происхождения с размерностью 1,3—1,5. Для примера: волны и облака имеют размерность 1,3, береговая линия — 1,05.

А что, если увеличить размерность? Получившийся объект не всегда будет приятно разглядывать. На иллюстрации выше изображена картина распределения электрического разряда с размерностью 1,75, известная как фигура Лихтенберга, созданная высоковольтным электрическим разрядом на непроводящем материале.

Еще один отталкивающий объект — фрактальный продукт кристаллических структур с размерностью 1,8, сфотографированный через микроскоп.

Демосцена & софт

Пожалуй, нигде так красочно не исследовали мир фракталов, как в демосцене. Hartverdrahtet — достойный победитель конкурса демосцены 2012 года по 4-килобайтным файлам. Автор, Demoscene Passivist, говорит, что для создания демо с процедурно генерируемыми фрактальными ландшафтами потребовалось около двух месяцев.

А вот один из лучших проектов с фрактальными эффектами в демосцене. К сожалению, качество демонстрационного видео крайне плохое (из-за давности лет), но демо можно скачать и запустить на компьютере.

Для создания подобных или других фрактальных миров особых ухищрений не требуется. Есть несколько отличных программ, с помощью которых вы сможете самостоятельно изучать особенности фрактальной вселенной.

XaoS Open Source Project. Бесплатный, открытый, кроссплатформенный инструмент для масштабирования и изучения множества Мандельброта и десятков других фракталов.

JWildfire. Еще одна кроссплатформенная (в том числе с мобильной версией) программа, основанная на Java с открытым исходным кодом, для обработки изображений. Она известна в основном своим сложным генератором пламенных фракталов.

Mandelbulber | Mandelbulb3D. Превосходные бесплатные инструменты для создания трехмерных фракталов, таких как устрашающая Оболочка Мандельброта, загадочная «коробка» Мандельбокс и др. Mandelbulber несколько более функционален и быстр, но Mandelbulb3D чуть проще в использовании.

По ссылке вы найдете множество других программ.

Источник

Бесконечность фракталов. Как устроен мир вокруг нас

Мы уже писали о том, как абстрактная математическая теория хаоса нашла применения в самых разных науках – от физики до экономики и политологии. Сейчас мы приведем еще один подобный пример – теорию фракталов. Строгого определения понятия «фрактал» нет даже в математике. Что-то там такое они, конечно, говорят. Но «простому человеку» этого не понять. Как вам, например, такая фраза: «Фрактал – это множество, обладающее дробной хаусдорфовой размерностью, которая больше топологической». Тем не менее, они, фракталы, окружают нас и помогают понять многие явления из разных сфер жизни.

С чего все началось

Фракталами долго никто кроме профессиональных математиков не интересовался. До появления компьютеров и соответствующего софта. Все изменилось в 1982 году, когда в свет вышла книга Бенуа Мандельброта «Фрактальная геометрия природы». Эта книга стала бестселлером, не столько по причине простого и понятного изложения материала (хотя это утверждение весьма относительно – человек, не имеющий профессионального математического образования в ней ничего не поймет), сколько из-за приведенных компьютерных иллюстраций фракталов, которые, действительно, завораживают. Давайте посмотрим на эти картинки. Они, правда, того стоят.

И таких картинок множество. Но какое все это великолепие имеет отношение к нашей реальной жизни и к тому, что окружает нас в природе и повседневном мире? Оказывается, самое прямое.

Но сначала скажем несколько слов о самих фракталах, как геометрических объектах.

Что такое фрактал, если говорить по-простому

Первое. Как они, фракталы, строятся. Это довольно сложная процедура, использующая специальные преобразования на комплексной плоскости (что это такое – знать не надо). Важно только то, что эти преобразования являются повторяющимися (происходят, как говорят в математике, итерациями). Вот в результате этого повторения и возникают фракталы (те, которые вы видели выше).

Второе. Фрактал является самоподобной (точно или приблизительно) структурой. Это значит следующее. Если вы поднесете к любой из представленных картинок микроскоп, увеличивающий изображение, например, в 100 раз, и посмотрите на фрагмент попавшего в окуляр кусочка фрактала, то вы обнаружите, что он идентичен исходному изображению. Если вы возьмете более сильный микроскоп, увеличивающий изображение в 1000 раз, то вы обнаружите, что кусочек попавшего в окуляр фрагмента предыдущего изображения имеет ту же самую или очень похожую структуру.

Из этого следует крайне важный для последующего вывод. Фрактал имеет крайне сложную структуру, которая повторяется на разных масштабах. Но чем больше мы забираемся вглубь его устройства, тем сложнее он становится в целом. И количественные оценки свойств первоначальной картинки могут начинать меняться.

Вот теперь мы оставим абстрактную математику и перейдем к окружающим нас вещам – таким, казалось бы, простым и понятным.

Фрактальные объекты в природе

Береговая линия

Представьте себе, что вы с околоземной орбиты фотографируете некий остров, например Британию. Вы получите такое же изображение, как на географической карте. Плавное очертание берегов, со всех сторон – море.

Узнать протяженность береговой линии очень просто. Возьмите обычную нитку и аккуратно выложите ее по границам острова. Потом, измеряйте ее длину в сантиметрах и, полученное число, умножайте на масштаб карты – в одном сантиметре сколько-то там километров. Вот и результат.

А теперь следующий эксперимент. Вы летите на самолете на высоте птичьего полета и фотографируете береговую линию. Получается картина, похожая на фотографии со спутника. Но эта береговая линия оказывается изрезанной. На ваших снимках появляются небольшие бухты, заливы, выступающие в море фрагменты суши. Все это соответствует действительности, но не могло быть увиденным со спутника. Структура береговой линии усложняется.

Допустим, прилетев домой, вы на основании своих снимков сделали подробную карту береговой линии. И решили измерить ее длину с помощью той самой нитки, выложив ее строго по полученным вами новым данным. Новое значение длины береговой линии превысит старое. И существенно. Интуитивно это понятно. Ведь теперь ваша нитка должна огибать берега всех заливов и бухт, а не просто проходить по побережью.

Заметьте. Мы уменьшили масштаб, и все стало намного сложнее и запутаннее. Как у фракталов.

А теперь еще одна итерация. Вы идете по тому же побережью пешком. И фиксируете рельеф береговой линии. Выясняется, что берега заливов и бухт, которые вы снимали с самолета, вовсе не такие гладкие и простые, как вам казалось на ваших снимках. Они имеют сложную структуру. И, таким образом, если вы нанесете на карту вот эту «пешеходную» береговую линию, длина ее вырастет еще больше.

Да, бесконечностей в природе не бывает. Но совершенно понятно, что береговая линия – это типичный фрактал. Она остается себе подобной, но ее структура становится все более и более сложной при ближайшем рассмотрении (вспомните про пример с микроскопом).

Это воистину удивительное явление. Мы привыкли к тому, что любой ограниченный по размерам геометрический объект на плоскости (квадрат, треугольник, окружность) имеет фиксированную и конечную длину своих границ. А здесь все по-другому. Длина береговой линии в пределе оказывается бесконечной.

Дерево

Дерево воспроизводит само себя, на каждом уровне. При этом его структура постоянно усложняется, но остается себе подобной. Это ли не фрактал?

Кровообращение

А вот кровеносная система человека. Она тоже имеет фрактальную структуру. Есть артерии и вены. По одним из них кровь подходит к сердцу (вены), по другим поступает от него (артерии). А далее, кровеносная система начинает напоминать то самое дерево, о котором мы говорили выше. Сосуды, сохраняя свое строение, становятся все более тонкими и разветвленными. Они проникают в самые отдаленные участки нашего тела, доносят кислород и другие жизненно важные компоненты до каждой клетки. Это типичная фрактальная структура, которая воспроизводит саму себя все в более и более мелких масштабах.

Стоки реки

«Из далека долго течет река Волга». На географической карте это такая голубая извилистая линия. Ну, притоки крупные обозначены. Ока, Кама. А если мы уменьшим масштаб? Выяснится, что притоков этих намного больше. Не только у самой Волги, но и у Оки и Камы. А у них есть и свои притоки, только более мелкие. А у тех – свои. Возникает структура, удивительно похожая на кровеносную систему человека. И опять возникает вопрос. Какова протяженность всей этой водной системы? Если измерять протяженность только основного русла – все понятно. В любом учебнике можно прочитать. А если все измерять? Опять в пределе бесконечность получается.

Наша Вселенная

Конечно, в масштабах миллиардов световых лет, она, Вселенная, устроена однородно. Но давайте посмотрим на нее поближе. И тогда мы увидим, что никакой однородности в ней нет. Где-то расположены галактики (звездные скопления), где-то – пустота. Почему? Почему распределение материи подчиняется иррегулярным иерархическим законам. А что происходит внутри галактик (еще одно уменьшение масштаба). Где-то звезд больше, где-то меньше. Где-то существуют планетные системы, как в нашей Солнечной, а где-то – нет.

Не проявляется ли здесь фрактальная сущность мира? Сейчас, конечно, существует огромный разрыв между общей теорией относительности, которая объясняет возникновение нашей Вселенной и ее устройством, и фрактальной математикой. Но кто знает? Возможно, это все когда-то будет приведено к «общему знаменателю», и мы посмотрим на окружающий нас космос совсем другими глазами.

К практическим делам

Подобных примеров можно приводить много. Но давайте вернемся к более прозаическим вещам. Вот, например, экономика. Казалось бы, причем здесь фракталы. Оказывается, очень даже причем. Пример тому – фондовые рынки.

Практика показывает, что экономические процессы носят зачастую хаотичный, непредсказуемый характер. Существовавшие до сегодняшнего дня математические модели, которые пытались эти процессы описывать, не учитывали одного очень важного фактора – способность рынка к самоорганизации.

Вот тут на помощь и приходит теория фракталов, которые имеют свойства «самоорганизации», воспроизводя себя на уровне разных масштабов. Конечно, фрактал является чисто математическим объектом. И в природе, да и в экономике, их не существует. Но есть понятие фрактальных явлений. Они являются фракталами только в статистическом смысле. Тем не менее симбиоз фрактальной математики и статистики позволяет получить достаточно точные и адекватные прогнозы. Особенно эффективным этот подход оказывается при анализе фондовых рынков. И это не «придумки» математиков. Экспертные данные показывают, что многие участники фондовых рынков тратят немалые деньги на оплату специалистов в области фрактальной математики.

Что же дает теория фракталов? Она постулирует общую, глобальную зависимость ценообразования от того, что было в прошлом. Конечно, локально процесс ценообразования случаен. Но случайные скачки и падения цен, которые могут происходить сиюминутно, имеют особенность собираться в кластеры. Которые воспроизводятся на больших масштабах времени. Поэтому, анализируя то, что было когда-то, мы можем прогнозировать, как долго продлиться та или иная тенденция развития рынка (рост или падение).

Таким образом, в глобальном масштабе тот или иной рынок «воспроизводит» сам себя. Допуская случайные флуктуации, вызванные массой внешних факторов, в каждый конкретный момент времени. Но глобальные тенденции сохраняются.

Вот вам и фракталы! Чем мы дальше уменьшаем масштаб, тем структура фрактала становится все более сложной. Но они воспроизводят себя, так же как это делает фондовый рынок.

Заключение

Почему мир устроен по фрактальному принципу? Ответ, возможно, состоит в том, что фракталы, как математическая модель, обладают свойством самоорганизации и самоподобия. При этом каждая их форма (см. приведенные в начале статьи картинки) сколь угодно сложна, но живет своей собственной жизнью, развивая себе подобные формы. Не так ли и наш мир устроен?

А вот общество. Появляется какая-нибудь идея. Сначала довольно абстрактная. А потом «проникает в массы». Да как-то трансформируется. Но в целом сохраняется. И превращается на уровне большинства людей в целеуказание жизненного пути. Вот тот же СССР. Принял очередной съезд КПСС очередные эпохальные решения, и пошло все это вниз. В более и более мелкие масштабы. Горкомы, парткомы. И так до каждого человека. Повторяющаяся структура.

Конечно, теория фракталов не позволяет нам прогнозировать будущие события. А это вряд ли и возможно. Но на многое то, что нас окружает, и что происходит в нашей повседневной жизни, позволяет смотреть совсем другими глазами. Осознанными.

Источник