Фракталы в трейдинге что это
Индикатор фракталов Билла Вильямса: как его использовать?
Индикатор фракталов был создан известным трейдером Биллом Вильямсом. Его можно использовать изолированно или вместе с другими индикаторами. Билл Вильямс также дает нам свой подход к применению фракталов в трейдинге, который мы также рассмотрим.
Билл Вильямс считается одним из прародителей современной торговой психологии. Еще в 1980-х годах он выдвинул теорию хаоса, которая предложила методологическое понимание рыночных структур. Он объединил торговую психологию с прикладным техническим анализом и разработал торговую систему, которая опередила свое время. Даже сегодня как розничные, так и институциональные трейдеры считают теорию хаоса и систему торговли по индикатору аллигатор одной из самых прибыльных торговых систем.
В соответствии со своей теорией хаоса, Вильямс разработал ряд технических индикаторов. Его подход к техническому анализу и правильному использованию индикаторов в сочетании с изложенными им правилами составляет основную часть торговой системы аллигатор.
Что из себя представляет индикатор фракталов?
Давайте для начала разберемся, что из себя представляют фракталы. Фракталы можно использовать:
Чтобы добавить индикатор фракталов на график в платформе MetaTrader нажмите: «Вставка» — «Индикаторы» — «Билла Вильямса» — «Fractals».
В природе фрактальные узоры встречаются в кристаллах, ветках деревьев и снежинках, и это лишь некоторые примеры. Фрактальные шаблоны являются рекурсивными, потому что независимо от целого, они строятся из множества повторений одной и той же модели.
Как это относится к трейдингу? Фракталы основаны на математической теории хаоса. В теории хаоса движение цены по своей природе фрактально: то есть рынок совершает одинаковые или похожие движения на всех таймфреймах. Ценовые паттерны кажутся случайными, но в них есть свой порядок, что объясняется волновой теорией Эллиотта.
Французский математик Бенуа Мандельброт был первым человеком, который обратил внимание на повторяющиеся ценовые модели. Анализ движения цены на хлопок за более чем столетний период привел его к созданию торговой стратегии, впервые упомянутой в известной книге Билла Уильямса «Торговый хаос». Именно Вильямс впервые предположил, что рынок является хаотичной и саморегулирующейся системой.
Фракталы указывают на вершины и впадины потенциального разворота рынка.
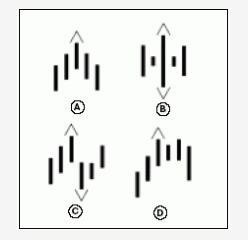
Визуально — это крошечные стрелки вверх и вниз. Чтобы сформировался фрактал, должна появиться серия из 5 последовательных свечей. При этом средняя свеча должна быть с самым высоким максимумом или низким минимумом по сравнению с двумя соседними свечами с каждой стороны:
Общие свечи у фракталов:
Фракталы показывают моментные развороты цены и определяют значимые точки в движении цены. Однако данные паттерны не могут быть идентифицированы как медвежьи или бычьи без учета общего рыночного контекста.
Индикатор фракталов как показатель пробоя
Поскольку фракталы выделяют точки разворота цены, логично, что как только цена совершит пробой предыдущего фрактала, возникает новый ценовой импульс.
Сделка на пробой фрактала является очевидным и самым простым применением данного индикатора. Также фракталы помогают определить ключевые уровни.
Фракталы как точки соединения линии тренда
Индикатор фракталов позволяет легко определять и связывать наиболее значимые вершины и впадины движения цены, необходимые для построения линий тренда. Рисование линий тренда с использованием фракталов может дать некоторое преимущество трейдерам, поскольку другие участники рынка также могут использовать те же очевидные ценовые точки.
Фракталы в тренде
В восходящем тренде мы видим все больше пробитых восходящих фракталов. В нисходящем тренде будет больше пробитых нисходящих фракталов. По мере продвижения тренда будет наблюдаться череда последовательных пробоев и появление новых фракталов. В случае неудачного пробоя фрактала мы получаем первые признаки бокового движения цены.
Неспособность успешно пробить предыдущий фрактал создает предпосылку для появления консолидации.
Использование фракталов по Биллу Вильямсу
Доктор Вильямс назвал фракталы первым измерением своей системы технического анализа. Фракталы — это, по сути, краткосрочные уровни поддержки и сопротивления на ценовом графике, и они являются фундаментальными строительными блоками торговой системы аллигатор.
Торговая система аллигатор является довольно сложной системой, поскольку она использует несколько различных индикаторов в сочетании с некоторыми правилами для входа в рынок, масштабирования позиций и имеет четко определенные правила о том, когда выходить из рынка.
Прелесть этой системы в том, что как только вы научитесь использовать индикаторы в сочетании с теорией хаоса, сканирование рынков и правильное понимание текущей тенденции или ее отсутствия станет для вас детской игрой.
По торговой системе Билла Вильямса, фракталы должны фильтроваться с помощью индикатора аллигатор.
Такие сигнальные фракталы будут оставаться действительными, пока не сработает ордер на вход или пока не будет сформирован новый фрактал. Тогда позиция должна быть изменена в соответствии с новым фракталом. Последовательные фракталы, которые возникают в том же направлении, что и сформированные после первого ордера, могут быть использованы для добавления в открытую позицию.
Индикатор аллигатор — ключ к использованию фракталов
Индикатор аллигатор состоит из трех скользящих средних:
Когда три скользящие средние расширяются и двигаются вверх, это сигнализирует о бычьем рынке. С другой стороны, когда скользящие средние расширяются и двигаются вниз, это сигнализирует о медвежьем рынке. Все очень просто.
По статистике, большинство рынков остаются в диапазоне примерно в 70% случаев, а тренды происходят только в 30% случаев. Поскольку торговая система аллигатор в основном представляет собой систему следования за трендом, отличительной особенностью индикатора аллигатор является то, что он может легко определить, находится ли рынок в тренде или торгуется в консолидации в пределах четко определенных уровней поддержки и сопротивления.
Когда скользящие средние значения аллигатора сжимаются, это сигнализирует о боковом рынке, и в соответствии с правилами системы вы должны оставаться вне рынка и ждать появления следующего тренда.
В торговой системе аллигатор есть несколько других индикаторов, таких как Awesome Oscillator и Accelerator Oscillator, которые используются для масштабирования позиций после того, как система сгенерирует свой первый сигнал. Однако, чтобы получить первый сигнал, вам необходимо хорошо понять, как работает индикатор фракталов.
Следовательно, как только вы определили трендовый рынок на основе сигнала аллигатора, вам нужно сначала искать фракталы, чтобы войти в сделку.
Как торговать по индикатору фракталов?
Согласно торговой системе аллигатор только потому, что сформирован фрактал вверх или вниз, это не означает, что это действительный сигнал. Вы должны интерпретировать фрактал по отношению к индикатору аллигатора и обратить внимание на зубы аллигатора.
Если верхний фрактал находится выше зубов аллигатора, только тогда он может считаться действительным. Напротив, если фрактал вниз формируется ниже зубов аллигатора, вы можете считать его действительным. Тем не менее, имейте в виду, что любой фрактал вверх, который сформировался ниже зубов аллигатора, недействителен и наоборот.
Как только вы найдете фрактал, который находится выше или ниже зубов аллигатора, подождите, пока аллигатор не начнет открывать свою челюсть, что происходит, когда три скользящие средние начинают расширяться.
Если индикатор аллигатор сигнализирует о восходящем тренде, разместите ордер Buy Stop немного выше фрактала вверх в направлении тренда. Точно так же, если индикатор аллигатор сигнализирует о нисходящем тренде, разместите ордер Sell Stop немного ниже фрактала вниз.
Можно ли прибыльно торговать используя фрактальность?
Фрактал Мандельброта (на картинке) – пожалуй, самый известный в широких кругах фрактал. Его назвали по имени человека, который, как считается, сделал наиболее весомый вклад в исследования принципа фрактальности.
Как же использовать фракталы в биржевом деле?
Читайте в сегодняшней статье:
Начни пользоваться ATAS абсолютно бесплатно! Первые две недели использования платформы дают доступ к полному функционалу с ограничением истории в 7 дней.
Фрактальность в окружающем нас мире
Окружающий нас мир – многообразный и невероятно сложный, и наблюдение за окружающей нас природой открывает перед человечеством удивительные математические закономерности. Очень много учёных черпали свои вдохновения для новых открытий из уже существующих творений в природе. Или математические открытия подтверждались явлениями в окружающем нас мире. Так, например, произошло с числами Фибоначи и фрактальностью.
Идея фракталов и фрактальности начала развиваться с 19 века (самый известный пример – “снежинка Коха”), а во второй половине 20 века получила активное развитие и применение во многих областях науки. Появление и развитие компьютерной техники дало толчок в применении принципа фрактальности в науке.
В чем заключается принцип фрактальности? Точного и общепринятого определения фрактала в научной среде не существует.
Если говорить простыми словами, фрактал – это объект, части которого подобны целому.
Признаки, по которым узнается фрактальность:
Очень многие объекты в живой природе фрактальны, то есть самоподобны.
Другими словами, фрактальность – это похожесть части на целое, и наоборот.
Понимая этот принцип, можно более точно описывать физические объекты, явления и окружающий нас мир в целом.
Фрактальность в трейдинге
Финансовые рынки состоят из миллионов людей, соответственно являются «живыми», постоянно изменяющимися, эволюционирующими, как и человеческое общество. Соответственно, закономерности, которые мы наблюдаем в живой природе, могут быть применены для описания и прогнозирования финансовых рынков. И одним из таких принципов и является фрактальность.
Фрактальность в природе и в трейдинге была хорошо описана и популяризирована Биллом Уильямсом в книге «Торговый хаос» ( что еще почитать трейдеру )
Но важно понимать ограничения любых книг, написанных о финансовых рынках. Чтобы собрать информацию для книги, написать ее, отредактировать и издать – чаще всего необходимо несколько лет. А так как рынки – это быстро развивающийся в эру информационных технологий «живой» организм, то к моменту издания книги, тем более, прочтения ее отдельным трейдером, информация, может потерять актуальность.
Могут устареть торговые системы, начать хуже работать и запаздывать торговые индикаторы, но базовые принципы, чаще всего остаются неизменными. Поэтому при чтении любой книги по трейдингу, важно искать и осознавать именно базовые принципы, а не конкретные торговые системы или индикаторы.
Объективно, принцип фрактальности будет актуален всегда, и изучение его применения на финансовых рынках стоит потраченного времени.
Теория хаоса
Важной идеей в трудах Билла Уильямса является теория хаоса. С помощью теории хаоса ученые пытаются описать окружающий нас мир и процессы в нем происходящие. В данной теории хаос – это не синоним беспорядка, а наоборот – высшая степень порядка, в которой процессы и явления происходят не спонтанно, а подчинены организующим принципам. Но стороннему наблюдателю, не понимающему этих принципов, кажется, что процесс беспорядочный (хаотичный).
Человеческий мозг, в данном смысле, тоже хаотичен, его работа подчинена организующим принципам, хотя на первый взгляд может казаться беспорядочной. Рынки – это продукт человеческого мозга, и они хаотичны по своей природе. Для описания хаотичных процессов должна применятся нелинейная логика, фрактальная геометрия. Если посмотреть на биржевые графики, то они могут быть подобны многим фрактальным проявлениям, например береговой линии, волнам моря, движению реки.
Если бы мы создавали мир, пользуясь только линейной логикой, у нас бы получились прямые деревья, круглые моря, и квадратные горы. Но окружающий нас мир абсолютно не такой. Линейная логика для описания нелинейных процессов не подходит. Это же касается и торговых систем, создаваемых трейдерами.
Какой будет результат, если нелинейный фрактальный биржевой график пытаться анализировать и прогнозироваться с помощью линейных математических формул (индикаторов), Евклидовой линейной геометрии (графического анализа)?
Идеального результата не будет. Для понимания нелинейности (фрактальности) рынка гораздо более подходят методы анализа текущего состояния рынка.
Текущее состояние нелинейного рынка – это меняющийся баланс / дисбаланс спроса и предложения. Понимание того, кто на рынке сейчас выигрывает борьбу (покупатели или продавцы), можно получить с помощью таких инструментов, как:
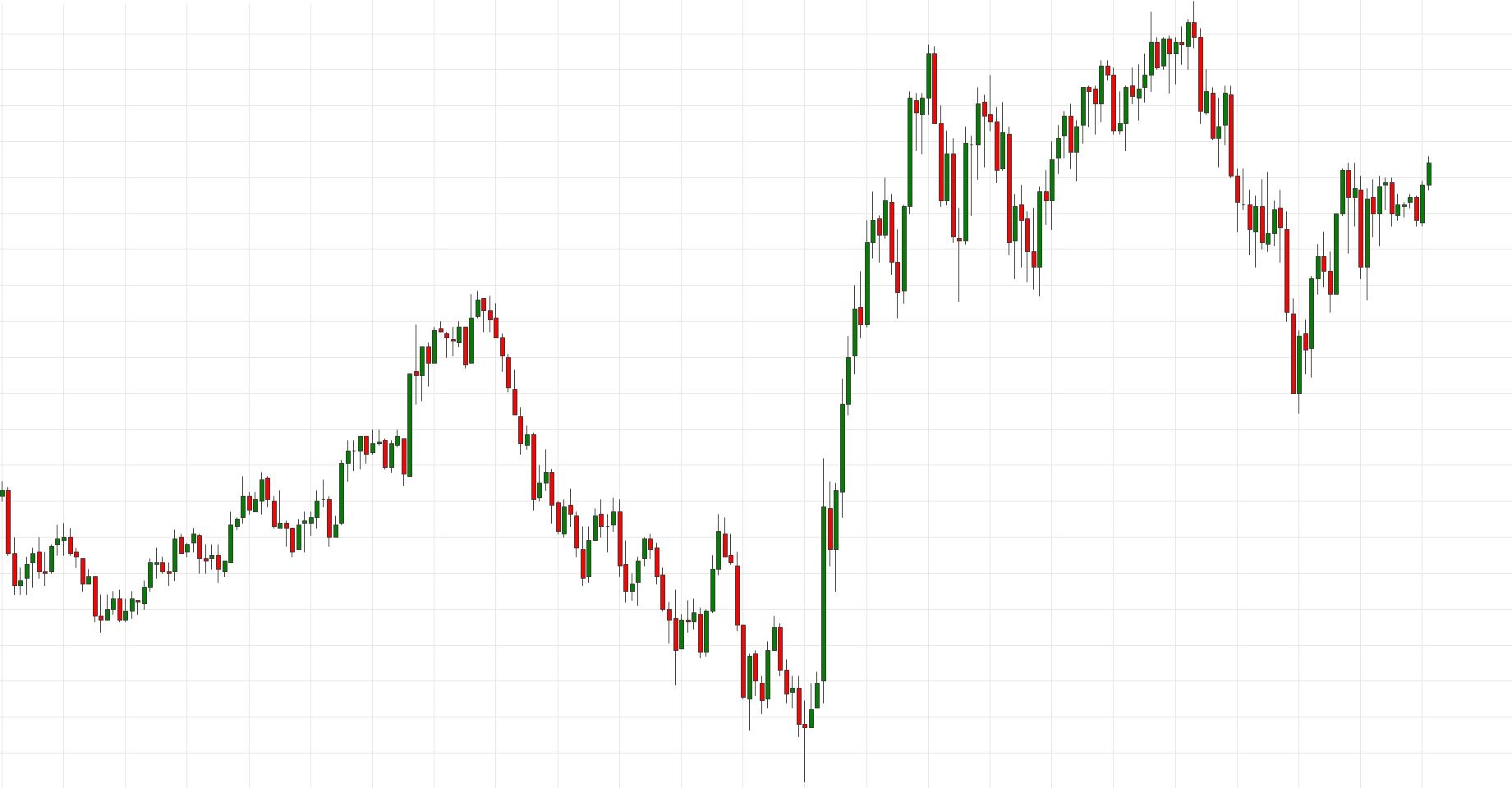
Фракталы на биржевых графиках
Биржевые графики обладают свойством фрактальности. Именно поэтому, смотря на график, крайне сложно определить, какой на нем представлен таймфрейм:
Такой график может соответствовать как 1 минутному таймфрейму, так и месячному.
Это и есть принцип фрактальности на биржевых графиках – малое подобно большому, и наоборот.
Для нас, трейдеров в этом есть неоспоримое преимущество. Ведь научившись торговать на одном таймфрейме, мы можем масштабировать нашу торговлю:
Хотя, конечно, у каждого таймфрейма есть свои особенности, но общий характер рыночных движений сохраняется благодаря фрактальности.
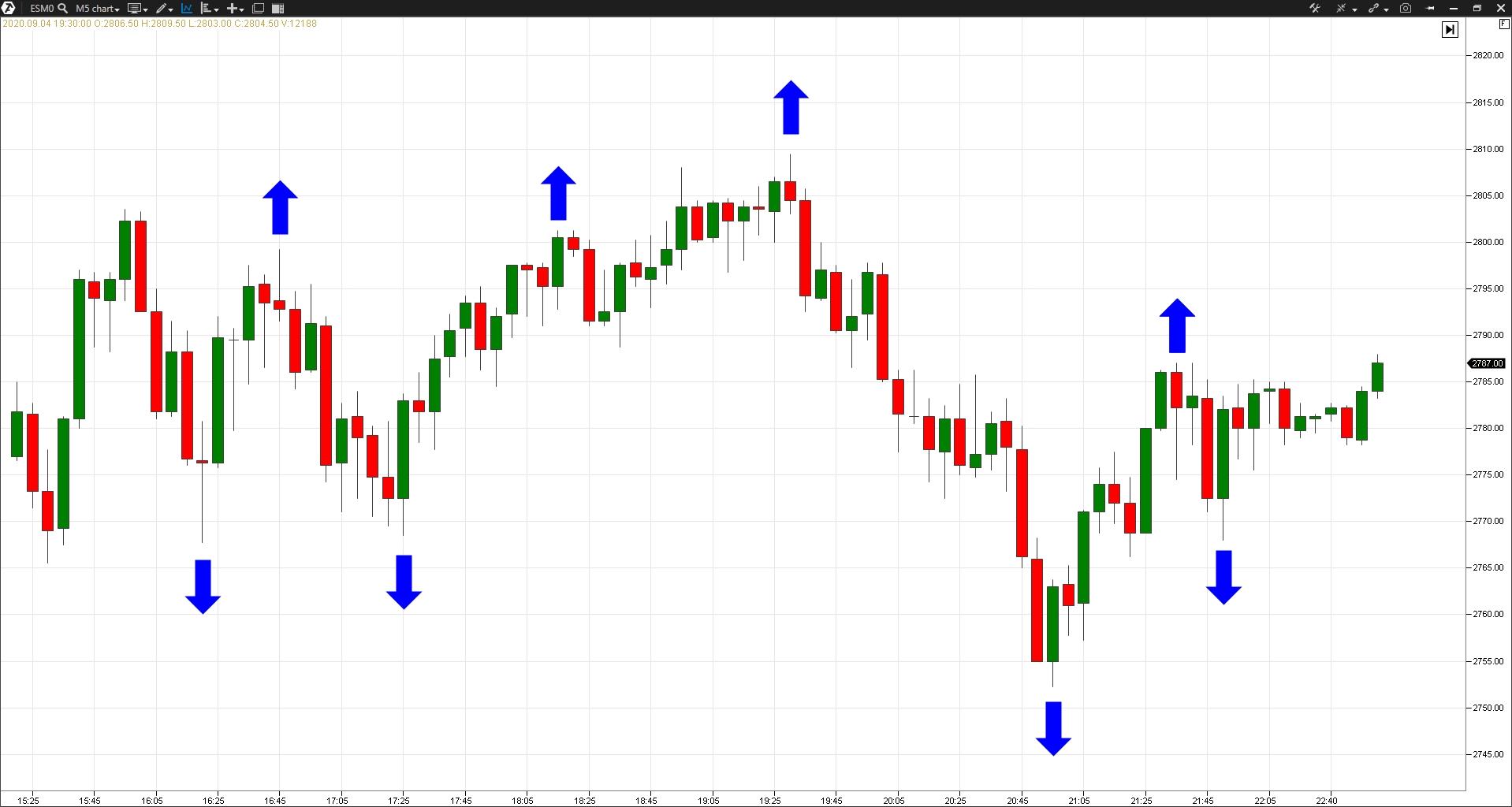
Фракталом в трейдинге принято называть локальный экстремум, состоящий из нескольких баров.
Стрелками на графике показаны фракталы, которые являются экстремумами – то есть, локальными минимумами или максимумами на текущем графике.
Билл Уильямс определяет, что:
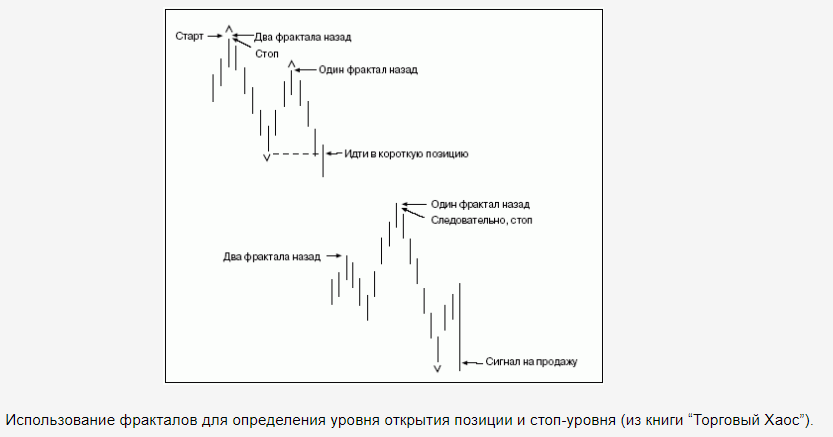
Как следствие, фракталы не могут появиться на самом правом краю графика. Для его образования, нужно, как минимум, 5 баров. Примеры того, какими могут быть фракталы, вы можете увидеть на картинке из книги “Торговый хаос”.
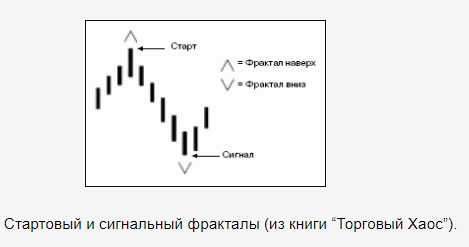
С целью построения стратегии торговли, основанной на фракталах, Билл Уильямс вводит также правила сигнального и стартового фракталов.
По классике Билла Уильямса, фракталы предлагается торговать на пробой (идея отображена на картинке ниже). Как альтернатива, используется стратегия “на отбой”.
Своей карьерой трейдера, и многочисленными примерами успехов последователей, Билл Уильямс подтвердил состоятельность подхода, основанного на фрактальности и подобию окружающему миру.
Можно улучшить ли торговлю по фракталам, используя современные программные решения для анализа рынков?
Прибыльная торговля по фракталам с помощью анализа объемов
Основная проблема торговли по фракталам – это многочисленные пробои фракталов-экстремумов.
По классической теории, трейдерам рекомендуется располагать стоп-лоссы за максимумы и минимумы на текущем графике. Как следствие, там скапливается большое количество защитных ордеров и коварный рынок часто “заглядывает” туда, чтобы “вытряхнуть” трейдеров. В таких случаях еще говорят – “происходит захват ликвидности”.
Чтобы не “уйти с рынка по стоп-лоссу”, нужно торговать в гармонии с крупным игроком.
Для этого требуется анализировать объемы с целью поиска тренда, который формируется важными участниками рынка. Тогда придет понимание, в каком направлении, вероятнее всего, направится цена. В том же направлении и открывать свои сделки.
Выявлять намерения крупного игрока помогает функционал торговой платформы ATAS.
Как торговать фракталы прибыльно на практике? Рассмотрим 2 подхода – активный и пассивный.
Пассивный подход в торговле по фракталам
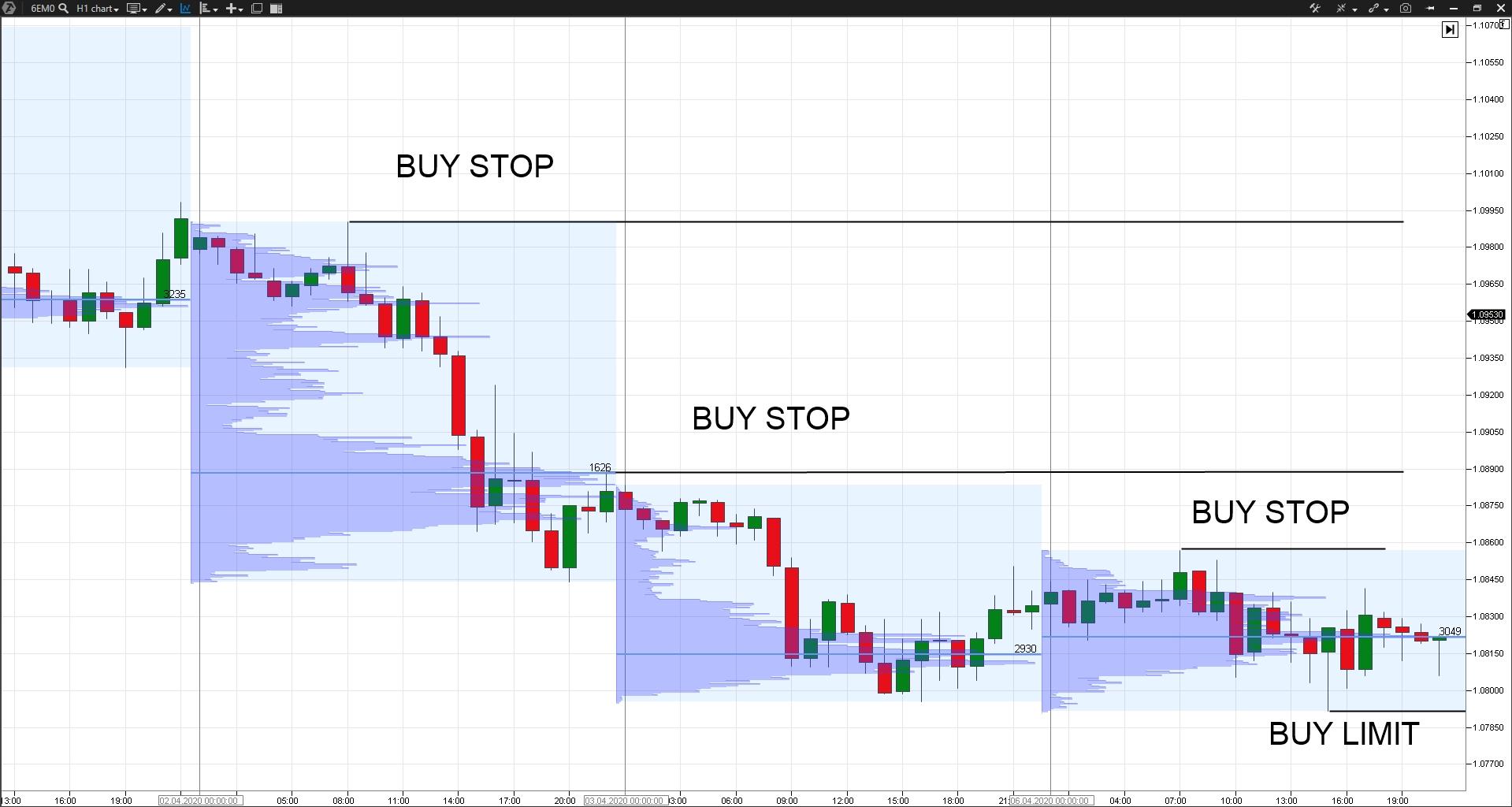
Исходя из этого простого наблюдения, можно выставлять отложенные ордера на пробой фракталов в соответствии с перемещением объема.
Например, вы определили, что на рынке присутствует бычий тренд (POC последней сессии выше POC предыдущей сессии). Тогда:
Далее контролируйте риски. Выбирайте такой размер лота, что даже при срабатывании нескольких ордеров и итоговом движении цены против вас, убытки не превысили 1-2% от депозита.
В конце американской сессии можно закрывать все сделки, независимо от результата.
Этот подход более спокойный, так как на анализ и выставление ордеров вы можете потратить не более 10 минут в день.
Активный поход в торговле по фракталам
Определите тренд (в каком направлении перемещается объём) и торгуйте в течение дня только в направлении тренда.
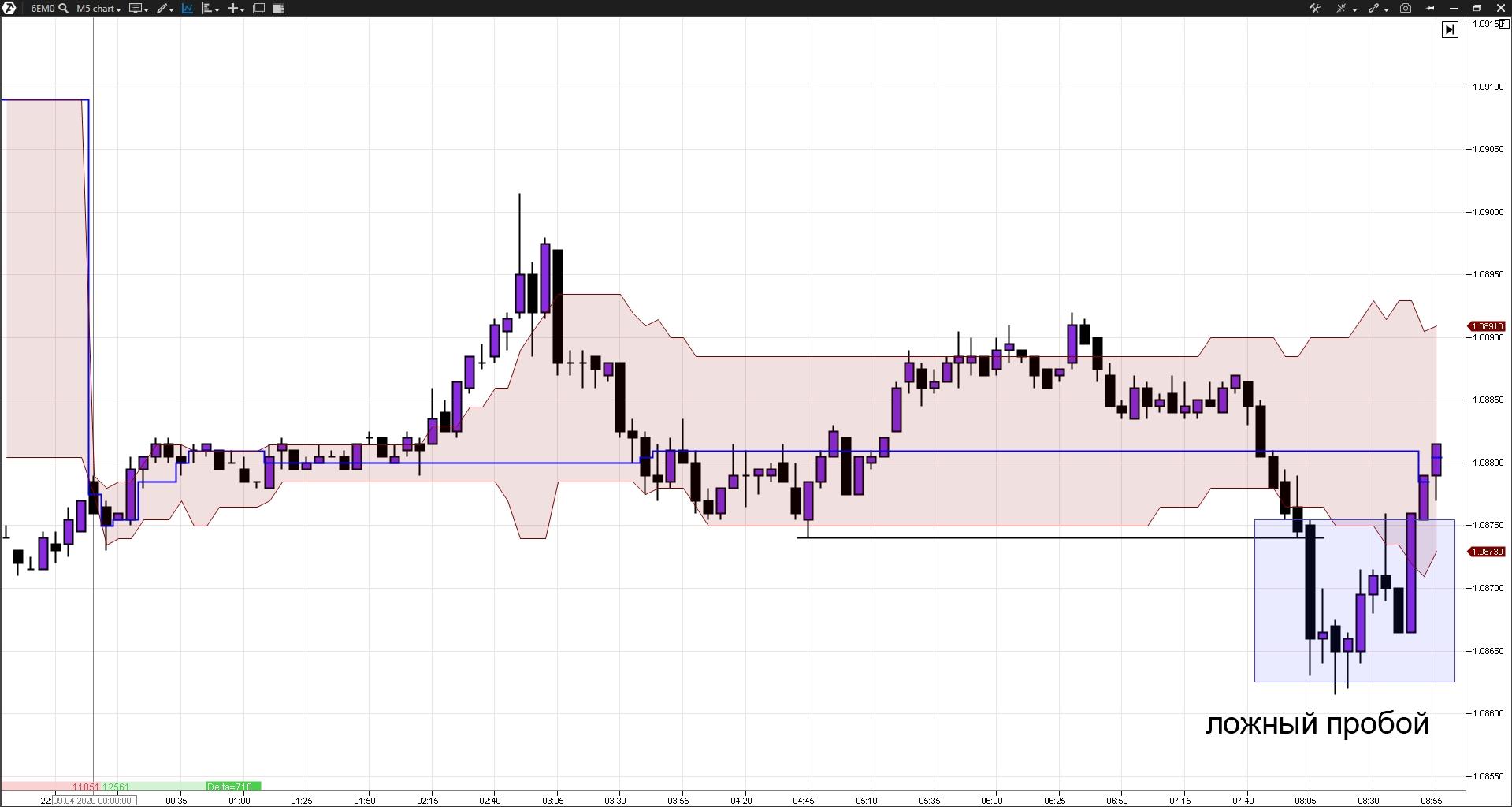
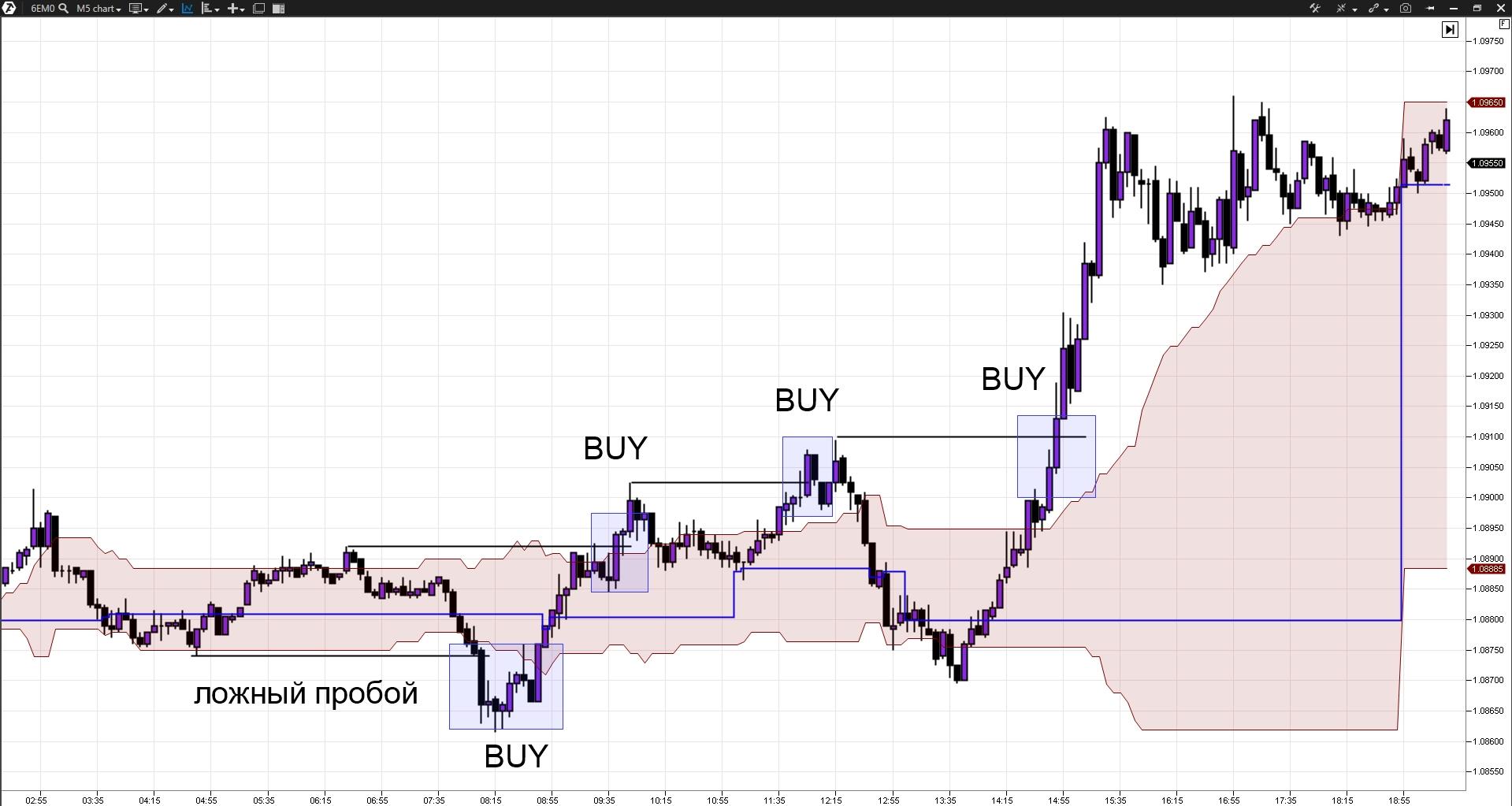
Если на рынке присутствует восходящий тренд, и внутри дня цена пробила нижний фрактал, выйдя из области Value area, а потом в неё вернулась – то, скорее всего, это был ложный пробой, и движение вверх вероятно продолжится.
Если на рынке присутствует восходящий тренд, и внутри дня цена пробила верхний фрактал, выйдя из области Value area – то, скорее всего, движение вверх продолжится.
Контролируйте риски, правильно выбирая размер позиции.
В конце американской сессии можно закрывать все сделки, независимо от результата.
Такой тип трейдинга позволит вам совершать сделки более точно, но будет требовать больше времени в день для работы.
Выводы
Окружающий нас мир нелинеен и фрактален. Рынки, как часть живой природы, как отражение особенностей работы человеческого мозга – тоже нелинейны и фрактальны. Рынки – это «живой» эволюционирующий организм, который описать с помощью простых формул или геометрических фигур крайне сложно.
Ввиду этого, на «живых рынках» дают погрешности:
Что хорошо работает на «живых рынках»:
На длительном промежутке времени, недостаточно четко на нелинейном рынке работают:
На длительном промежутке времени на нелинейном рынке лучше работают:
Итак, фракталы – это важный инструмент для торговли нелинейных рынков. Совмещая фракталы с анализом объемов, вы сможете торговать более устойчиво и стабильно. Чего вам и желаем!
Фракталы на Форекс – что нужно знать

Фракталы применяются на финансовых рынках уже довольно давно – даже в классических торговых стратегиях есть упоминания о них. Например, известная торговая стратегия Билла Вильямса Profitunity использует фракталы как один из элементов системы. Сегодня этот индикатор – герой нашего обзора: мы узнаем историю его появления, посмотрим, какие бывают фракталы, а в теме на форуме вы сможете ознакомиться более чем с сотней разновидностей этого индикатора)
Что такое фрактал?
У понятия «фрактал» нет строгого определения. Поэтому это слово не является математическим термином. Обычно так называют геометрическую фигуру, которая удовлетворяет одному или нескольким из следующих свойств:
– обладает сложной структурой при любом увеличении;
– является (приближенно) самоподобной;
– обладает дробной хаусдорфовой (фрактальной) размерностью, которая больше топологической;
– может быть построена рекурсивными процедурами.
История возникновения
На рубеже XIX и XX веков изучение фракталов носило скорее эпизодический, нежели систематический характер. Раньше математики, в основном, изучали объекты, которые поддавались исследованию при помощи общих методов и теорий.
В 1872 году немецкий математик Карл Вейерштрасс построил пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».
Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.
Другой класс — динамические, или алгебраические фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении относятся к началу XX века и связаны с именами французских математиков Гастона Жюлиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный труд Жюлиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жюлиа – целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то, что это работа прославила Жюлиа среди математиков того времени, о ней довольно быстро забыли.
Вновь внимание к работам Жюлиа и Фату обратилось лишь полвека спустя, с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов. Ведь Фату никогда не мог посмотреть на изображения, которые мы сейчас знаем, как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Первым, кто использовал для этого компьютер, был Бенуа Мандельброт.
В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей.
Благодаря иллюстрациям, полученным при помощи компьютера и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди не математиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения.
Когда персональные компьютеры стали достаточно мощными, то появилось даже целое направление в искусстве – фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой тематике.
После этого краткого экскурса в историю давайте, теперь, ознакомимся с классификацией типов фракталов на сегодняшний день.
Геометрические фракталы
Именно с них, как вы уже поняли, и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Сначала изображается основа. Затем некоторые части основы заменяются на фрагмент. На каждом следующем этапе части уже построенной фигуры, аналогичные замененным частям основы, вновь заменяются на фрагмент, взятый в подходящем масштабе. Всякий раз масштаб уменьшается. Когда изменения становятся визуально незаметными, считают, что построенная фигура хорошо приближает фрактал и дает представление о его форме. Для получения самого фрактала нужно бесконечное число этапов. Меняя основу и фрагмент – можно получить много разных геометрических фракталов.
Геометрические фракталы хороши тем, что, с одной стороны, являются предметом достаточного серьезного научного изучения, а с другой стороны – их можно увидеть. Даже человек, далекий от математики, найдет в них что-то для себя. Такое сочетание редко в современной математике, где все объекты задаются с помощью непонятных слов и символов.
Многие геометрические фракталы можно нарисовать буквально на листочке бумаги в клетку. Важно понимать, что все получаемые изображения являются лишь конечными приближениями бесконечных, по своей сути, фракталов. Но всегда можно нарисовать такое приближение, что глаз не будет различать совсем мелкие детали и наше воображение сможет создать верную картину фрактала.
Например, имея достаточно большой лист миллиметровой бумаги и запас свободного времени, можно вручную нарисовать такое точное приближение к ковру Серпинского, что с расстояния в несколько метров невооруженный глаз будет воспринимать его как настоящий фрактал. Компьютер позволит сэкономить время и бумагу и при этом еще увеличить точность рисования.
Снежинка Коха
Это один из самых первых исследованных учеными фракталов. Снежинка получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше, но кривая Коха замечательна простотой своей конструкции.
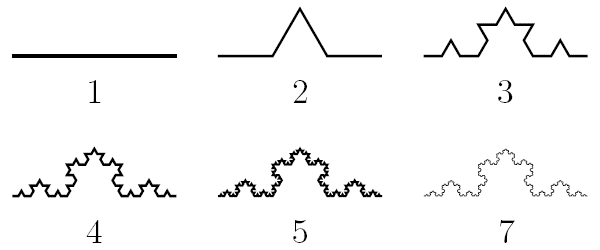
Кривая Коха имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)n–1. Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.
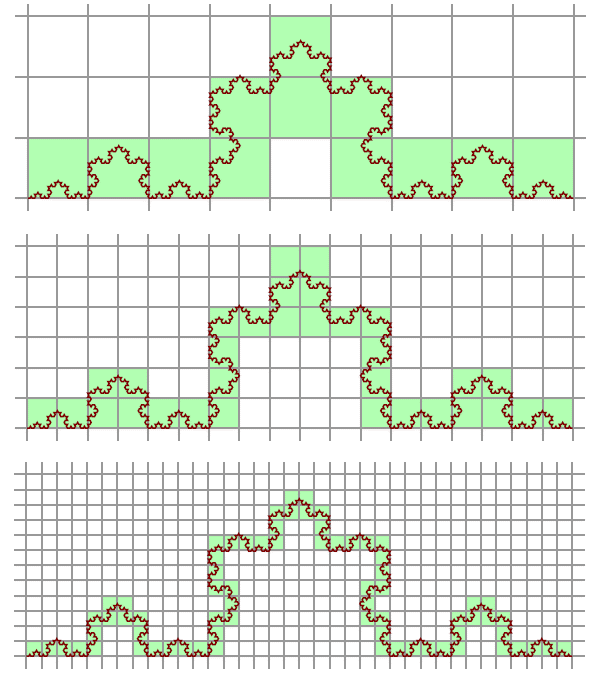
Снежинка Коха «наоборот»
Снежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника.

Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке ниже угол равен 88°.
Тут достраиваются квадраты.
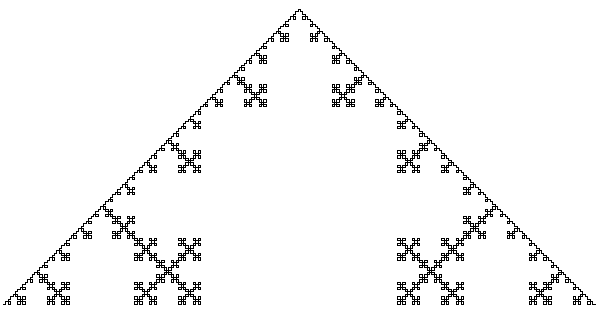
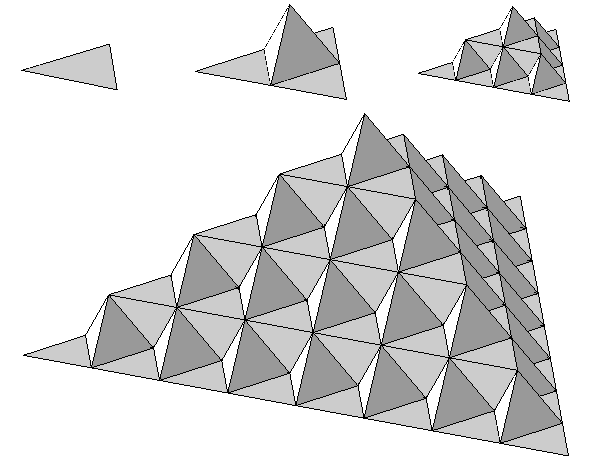
Построение начинается с единичного квадрата. Первый шаг: закрасить в центре белым цветом квадрат со стороной 1/2. Затем нужно мысленно разделить квадрат на 4 одинаковых и в центре каждого из них закрасить квадрат со стороной 1/4. Дальше каждый из этих 4 квадратов снова делится на 4 части, всего получится 16 квадратиков, и с каждым из них нужно проделать то же самое. И так далее.

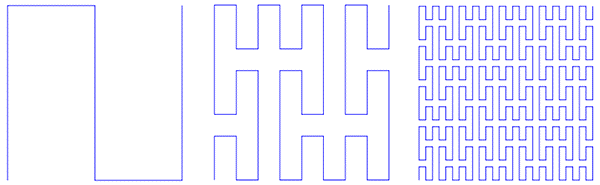
H-фрактал
Всё начинается с фигуры в виде буквы Н, у которой вертикальные и горизонтальные отрезки равны. Затем к каждому из 4 концов фигуры пририсовывается ее копия, уменьшенная в два раза. К каждому концу (их уже 16) пририсовывается копия буквы Н, уменьшенная уже в 4 раза. И так далее. В пределе получится фрактал, который визуально почти заполняет некоторый квадрат. Н-фрактал всюду плотен в нём. То есть в любой окрестности любой точки квадрата найдутся точки фрактала. Очень похоже на то, что происходит с Т-квадратом. Это не случайно, ведь, если присмотреться, видно, что каждая буква Н содержится в своем маленьком квадратике, который был дорисован на таком же шаге.
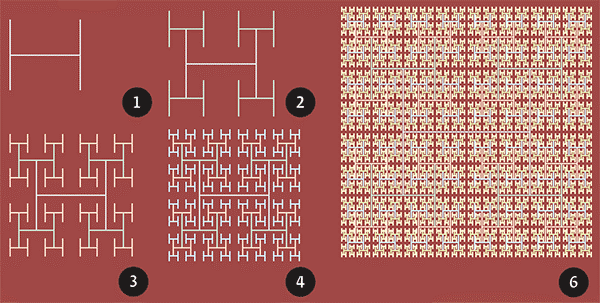
Принцип построения Н-фрактала применяют при производстве электронных микросхем: если нужно, чтобы в сложной схеме большое число элементов получило один и тот же сигнал одновременно, то их можно расположить в концах отрезков подходящей итерации Н-фрактала и соединить соответствующим образом.
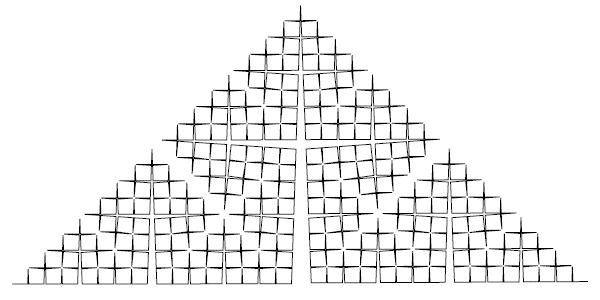
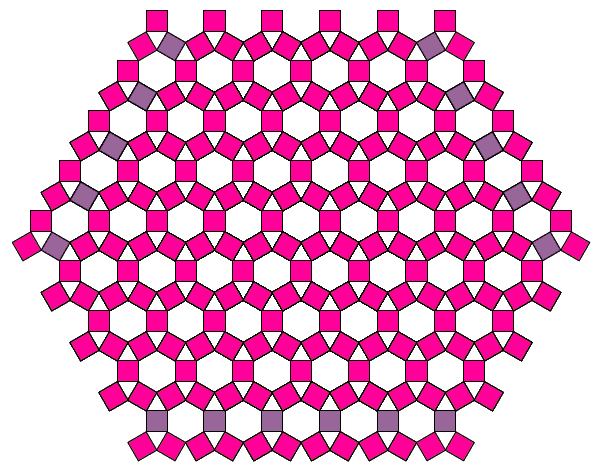
Дерево Мандельброта
Дерево Мандельброта получается, если рисовать толстые буквы Н, состоящие из прямоугольников, а не из отрезков:
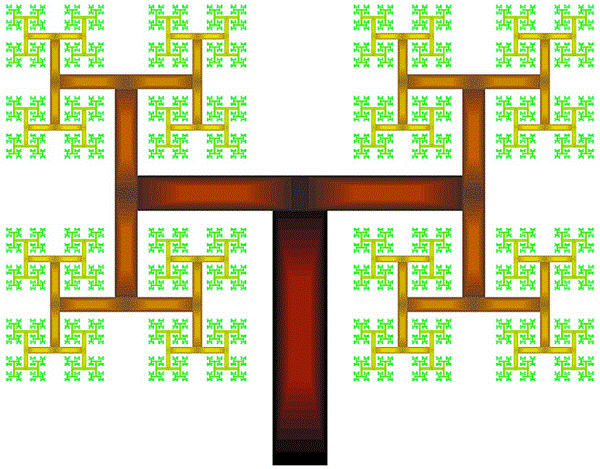
Называется так потому, что каждая тройка попарно соприкасающихся квадратов ограничивает прямоугольный треугольник и получается картинка, которой часто иллюстрируют теорему Пифагора – «пифагоровы штаны во все стороны равны».
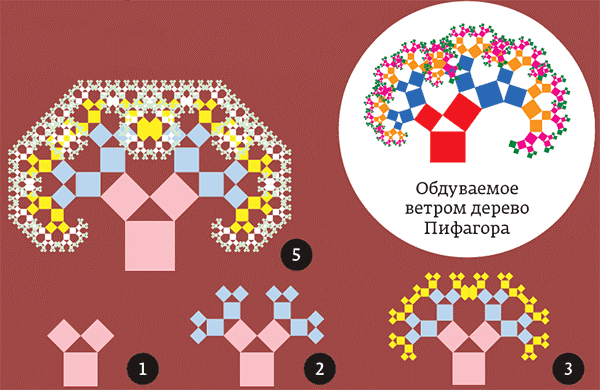
Если менять углы при основании треугольника, то будут получаться немного другие формы дерева. А при угле 60° все три квадрата окажутся равными, а дерево превратится в периодический узор на плоскости:
Кривая Пеано
Впервые такой объект появился в статье итальянского математика Джузеппе Пеано в 1890 году. Пеано пытался найти хоть сколько-нибудь наглядное объяснение того, что отрезок и квадрат равномощны (если рассматривать их как множества точек), то есть в них «одинаковое» количество точек. Эта теорема была ранее доказана Георгом Кантором в рамках придуманной им теории множеств. Однако подобные противоречащие интуиции результаты вызывали большой скепсис по отношению к новой теории. Пример Пеано — построение непрерывного отображения из отрезка на квадрат — стал хорошим подтверждением правоты Кантора.
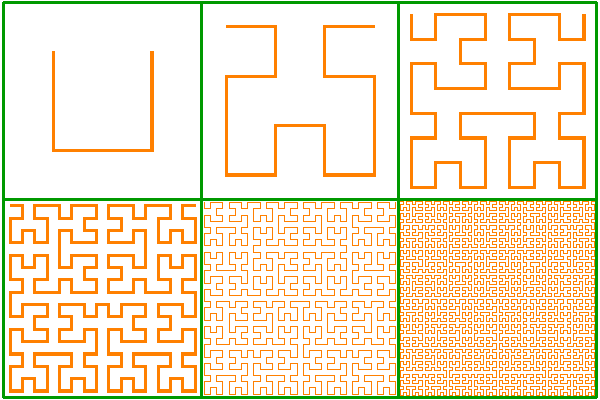
Кривая Гильберта
Фрактал «Греческий крест»
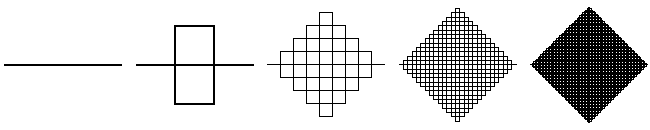
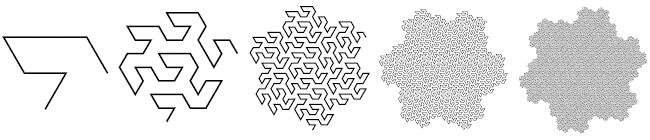
Кривая Госпера
Кривая Леви
Хотя этот объект изучал еще итальянец Эрнесто Чезаро в 1906 году, его самоподобие и фрактальные свойства исследовал в 1930-х годах француз Поль Пьер Леви. Фрактальная размерность границы этого фрактала примерно равна 1,9340. Но это довольно сложный математический результат, а точное значение неизвестно.

Куб Гильберта
А есть еще и трехмерные аналоги таких линий. Например, трехмерная кривая Гильберта, или куб Гильберта.

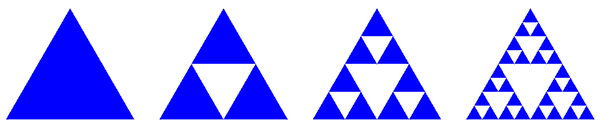
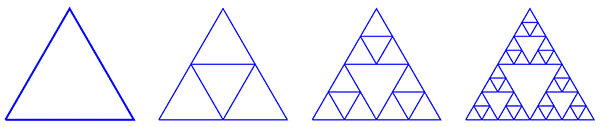
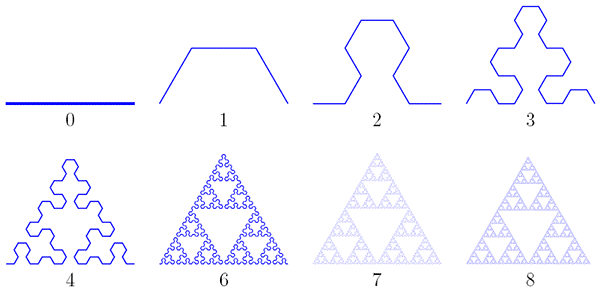
Треугольник Серпинского
Ковер (квадрат, салфетка) Серпинского
На треугольниках уважаемый математик не остановился и 1916 году им была описана квадратная версия. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата. Как и треугольник, квадрат можно получить из разных конструкций. Справа изображен классический способ: разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т.д.

Пирамида Серпинского

Губка Менгера
Обобщение ковра Серпинского в трехмерное пространство. Чтобы построить губку, нужно бесконечное повторение процедуры: каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших. Поэтому фрактальная размерность равна log320. Этот фрактал является универсальной кривой: любая кривая в трехмерном пространстве гомеоморфна некоторому подмножеству губки. У губки нулевой объем (так как на каждом шаге он умножается на 20/27), но при этом бесконечно большая площадь.

Динамические (алгебраические) фракталы
Фракталы этого типа возникают при исследовании нелинейных динамических систем (отсюда и название). Поведение такой системы можно описать комплексной нелинейной функцией (многочленом) f(z).
Множества Жюлиа
Возьмем какую-нибудь начальную точку z0 на комплексной плоскости. Теперь рассмотрим бесконечную последовательность чисел на комплексной плоскости, каждое следующее из которых получается из предыдущего: z0, z1 = f(z0), z2 = f(z1), … zn+1 = f(zn). В зависимости от начальной точки z0 такая последовательность может вести себя по-разному: стремиться к бесконечности при n → ∞; сходиться к какой-то конечной точке; циклически принимать ряд фиксированных значений; возможны и более сложные варианты.
Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f(z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жюлиа для функции f(z).
Множество Мандельброта
Оно строится немного иначе. Рассмотрим функцию fc(z) = z2 + с, где c — комплексное число. Построим последовательность этой функции с z0 = 0, в зависимости от параметра с она может расходиться к бесконечности или оставаться ограниченной. При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта. Оно было детально изучено самим Мандельбротом и другими математиками, которые открыли немало интересных свойств этого множества.
Видно, что определения множеств Жюлиа и Мандельброта похожи друг на друга. На самом деле эти два множества тесно связаны. А именно, множество Мандельброта — это все значения комплексного параметра c, при которых множество Жюлиа fc(z) связно (множество называется связным, если его нельзя разбить на две непересекающиеся части, с некоторыми дополнительными условиями).
Фрактал Галлея
Такие фракталы получаются, если в качестве правила для построения динамического фрактала использовать формулу Галлея для поиска приближенных значений корней функции. Формула довольно громоздкая, так что кто хочет, может посмотреть ее в Википедии. Идея метода почти та же, что используется для рисования динамических фракталов: берем какое-нибудь начальное значение (как обычно, здесь речь идет о комплексных значениях переменных и функций) и применяем к нему много раз формулу, получая последовательность чисел. Почти всегда она сходится к одному из нулей функции (то есть значению переменной, при котором функция принимает значение 0). Метод Галлея, несмотря на громоздкость формулы, работает эффективнее метода Ньютона: последовательность сходится к нулю функции быстрее.
Фрактал Ньютона
Применение фракталов в промышленности и быту
Ученые – очень увлеченные личности. Их хлебом не корми, дай пофантазировать на абстрактные темы. Но мы с вами люди практичные, и, прочитав все то, что написано выше, у многих уже наверняка возник резонный вопрос: «ну и че?». Так вот, что же все-таки привнесло это знание в мир?
Во-первых, фракталы используются в компьютерных системах, причем очень плотно. Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.
Во-вторых, это механика жидкостей и, как следствие, нефтяная промышленность. Дело в том, что изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к их фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков. При помощи фракталов также можно смоделировать языки пламени. Пористые материалы хорошо представляются во фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке.
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который жил тогда в центре Бостона, где была запрещена установка на зданиях внешних антенн. Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы такой антенны не изучены до сих пор, это не помешало Коэну обосновать собственную компанию и наладить их серийный выпуск. В данный момент американская фирма Fractal Antenna System разработала антенну нового типа. Теперь можно отказаться от использования в мобильных телефонах торчащих наружных антенн – так называемая фрактальная антенна располагается прямо на основной плате внутри аппарата.
Кроме того, фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов. Еще они используются в разработке биосенсорных взаимодействий, исследованиях биения сердца, моделировании хаотических процессов, в частности при описании моделей популяций животных и так далее.
Фрактальная структура рынка
Вся эта ода фракталам была бы напрасной, если бы не фрактальная природа финансовых рынков. Да, наконец мы дошли до обсуждения того самого вопроса, ради которого я эту статью и писал.
Итак, в настоящее время применяется много способов анализа финансовых рынков, на основе которых трейдеры создают свои торговые стратегии. Среди различных инструментов анализа и прогноза фрактальный анализ стоит немного в стороне. Это отдельная разносторонняя и интересная теория для обсуждения и изучения. Первое впечатление говорит о простоте тематики, однако копни глубже, и будет видно много скрытых нюансов.
Понимание фракталов – это ключ к видению скрытой информации о рынке. А ведь именно она является одним из ключевых факторов рыночного успеха спекулянта и залогом большой стабильной прибыли.
14 октября 2010 года ушел из жизни Бенуа Мандельброт — человек, во многом изменивший наше представление об окружающих нас предметах и обогативший наш язык словом «фрактал».

Важнейшим классом природных фракталов являются хаотические временные ряды, или упорядоченные во времени наблюдения характеристик различных природных, социальных и технологических процессов. Среди них имеются как традиционные (геофизические, экономические, медицинские), так и те, которые стали известными относительно недавно (ежедневные колебания уровня преступности или ДТП в регионе, изменения количества показов определенных сайтов в интернете и т.д.). Эти ряды, обычно, порождаются сложными нелинейными системами, которые имеют самую различную природу. Однако у всех характер поведения повторяется на разных масштабах. Наиболее популярными их представителями являются финансовые временные ряды (в первую очередь цены акций и курсы валют).
Самоподобная структура таких рядов известна очень давно. В одной из своих статей Мандельброт писал, что его интерес к котировкам на фондовом рынке начался с высказывания одного из биржевиков: «…Движения цен большинства финансовых инструментов внешне похожи на разных масштабах времени и цены. По внешнему виду графика наблюдатель не может сказать, относятся данные к недельным, дневным или же часовым изменениям».
Мандельброт, занимающий совершенно особое место в финансовой науке, имел славу «ниспровергателя основ», вызывая среди экономистов явно неоднозначное к себе отношение. С момента возникновения современной финансовой теории, основанной на концепции общего равновесия, он был одним из главных ее критиков и до конца жизни пытался найти ей приемлемую альтернативу. Однако именно Мандельброт разработал систему понятий, которая при соответствующей модификации, как оказалось, позволяет не только построить эффективный прогноз, но и предложить, видимо, единственное на данный момент эмпирическое обоснование классической теории финансов.
Основной характеристикой фрактальных структур является фрактальная размерность D, введенная Феликсом Хаусдорфом в 1919 году. Для временных рядов чаще используют индекс Херста H, который связан с фрактальной размерностью соотношением D = 2 – H и является показателем персистентности (способности сохранять определенную тенденцию) временного ряда.
Обычно различают три принципиально разных режима, которые могут существовать на рынке: при Н = 0,5 поведение цен описывается моделью случайного блуждания; при Н > 0,5 цены находятся в состоянии тренда (направленного движения вверх или вниз); при H