Фрактация что это такое

Фрактал

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической.

Содержание

Термин

Слово «фрактал» может употребляться не только как математический термин. Фракталом в прессе и научно-популярной литературе могут называть фигуры, обладающие какими-либо из перечисленных ниже свойств:

Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, снежинки, кровеносная система и система альвеол человека или животных.

Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.

История

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например,функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Примеры

Самоподобные множества с необычными свойствами в математике

Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:

Рекурсивная процедура получения фрактальных кривых

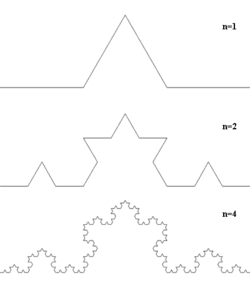
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены четыре первых шага этой процедуры для кривой Коха.

Примерами таких кривых служат:

С помощью похожей процедуры получается дерево Пифагора.

Фракталы как неподвижные точки сжимающих отображений

Свойство самоподобия можно математически строго выразить следующим образом. Пусть — сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости:

Можно показать, что отображение является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.

Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения — отображения подобия, а — число звеньев генератора.

Для треугольника Серпинского и отображения , , — гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении .

В случае, когда отображения — преобразования подобия с коэффициентами 0″ border=»0″ />, размерность фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения . Так, для треугольника Серпинского получаем .

По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения , мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.

Фракталы в комплексной динамике

Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа.

Нас интересует поведение этой последовательности при стремлении n к бесконечности. Эта последовательность может:

Множества значений z₀, для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.

Так, множество Жюлиа — множество точек бифуркации для многочлена F(z)=z 2 +c (или другой похожей функции), то есть тех значений z₀, для которых поведение последовательности <z_n> может резко меняться при сколь угодно малых изменениях z₀.

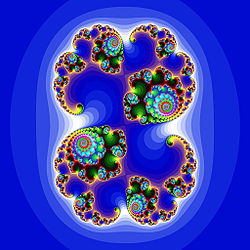
Другой вариант получения фрактальных множеств — введение параметра в многочлен F(z) и рассмотрение множества тех значений параметра, при которых последовательность <z_n> демонстрирует определённое поведение при фиксированном z₀. Так, множество Мандельброта — это множество всех , при которых <z_n> для F(z)=z 2 +c и z₀ не стремится к бесконечности.

Ещё один известный пример такого рода — бассейны Ньютона.

Популярно создание красивых графических образов на основе комплексной динамики путём раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления <z_n> к бесконечности (определяемой, скажем, как наименьший номер n, при котором |z_n| превысит фиксированную большую величину A.

Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.

Стохастические фракталы

Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:

В природе

Применение

Естественные науки

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

Радиотехника

Фрактальные антенны

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.

Информатика

Сжатие изображений

Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован [источник не указан 779 дней] фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.

Компьютерная графика

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см. Генератор фракталов (программа).

Децентрализованные сети

Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.

Экономика и финансы

А. А. Алмазов в своей книге «Фрактальная теория. Как поменять взгляд на рынки» предложил способ использования фракталов при анализе биржевых котировок, в частности — на рынке Форекс.

Источник

Созерцание великого фрактального подобия

(с) «Галактика галактик»

Фракталы — не просто красивое природное явление. Согласно проведенным исследованиям, рассматривание фрактальных структур на 60 % повышает стрессоустойчивость, измеряемую на основе физиологических показателей. При созерцании фракталов в лобной коре головного мозга всего за одну минуту увеличивается активность альфа-волн — как во время медитации или при ощущении легкой сонливости.

Неудивительно, что фрактальный биодизайн оказывает на человека умиротворяющее воздействие. Нам нравится смотреть на облака, на языки пламени в камине, на листву в парке… Как это работает? Ученые предполагают, что естественный ход поисковых движений наших глаз — фрактальный. При совпадении размерности траектории движения глаз и фрактального объекта мы впадаем в состояние физиологического резонанса, за счет чего активизируется деятельность определенных участков мозга.

Но не все фракталы одинаково полезны. В данной статье расскажем о фрактальной размерности и о её влиянии на здоровье.

Биофракталы

(с)

Примеры фракталов в природе встречаются повсеместно: от ракушек до сосновых шишек. Каждый фрактал имеет математическую размерность D. Для человека наиболее полезны фракталы с размерностью 1,3—1,5, и большинство фрактальных объектов, созданных природой, имеют именно такую размерность. А глаз человека эстетически «настроен» на восприятие как раз таких, встречающихся в природе фракталов.

Прекрасным примером фракталов в природе являются деревья. Фракталы можно обнаружить на каждом уровне лесной экосистемы — от семян и сосновых шишек до ветвей и листьев. На иллюстрации выше запечатлена «застенчивая крона» — явление, когда кроны деревьев не соприкасаются, формируя локальные участки лесного полога.

С биологической точки зрения такое расположение крон объясняется естественным отбором — листья расположены как можно дальше друг от друга, чтобы максимизировать доступ к ресурсам, особенно к солнечному свету для фотосинтеза.

Итальянская капуста романеско имеет сверхэффективную конструкцию, позволяющую максимизировать воздействие солнечного света и транспортировать питательные вещества по всей клеточной структуре растения.

Однако размерность этой капусты — 2,66. Вообще, дробная размерность является ключевой особенностью фракталов. При этом большинство из них находится в плоскости между линией (размерность 1) и двухмерной поверхностью (размерность 2). Чем выше показатель, тем больше движение в сторону трехмерных объектов (размерность 3).

Компьютерные игры

Трехмерные фракталы — одни из самых редких в природе. Гораздо проще встретить их в виртуальной реальности. Например, в игре Marble Marcher — уникальной аркаде, где нужно прокатить шар к цели в пространстве, созданном единым всеобъемлющим алгоритмом. Практически все, что вы увидите в игре, создано не дизайнерами, а чистой математикой.

Yedoma Globula — это 3D-песочница на самописном движке, в которой можно исследовать процедурно создаваемые фрактальные ландшафты.

Фрактальные формулы можно использовать в компьютерной графике для создания реалистичных гор, рек, лесов и облаков. Игра Everything пошла гораздо дальше: в ней помимо визуальной составляющей в системообразующей части геймплея использовано фрактальное подобие. Тут фактически нет NPC-персонажей. Вы можете начать игру в образе свиньи, которая бродит по зеленым склонам и встречает дуб, а затем стать дубом, который отправится в самостоятельное путешествие.

Гаджеты

Использовать фракталы как «что-то полезное» можно не только в компьютерных играх или для релаксации. Именно фракталы подсказали способ уменьшения размера антенн для сотовых телефонов. Фрактальная геометрия расширяет способность создавать новые, более практичные устройства.

Сейчас фракталы используются в новом поколении спутниковой связи, в устройствах IoT и других проектах приема, передачи и преобразования радиоволн.

Архитектура

Фракталы можно использовать даже неосознанно. На фото выше изображен фрагмент купола иранской мечети. А здесь вы найдете множество фотографий потолков школ, культурных и религиозных сооружений в Иране, которые демонстрируют невероятно сложные фрактальные рельефы и мозаики, декорирующие изысканные архитектурные элементы.

Храм Деви Джагадамби в Кхаджурахо — отличный пример фрактальной архитектуры. Индийские и многие другие храмы Юго-Восточной Азии имеют фрактальную структуру: главная башня окружена башнями меньшего размера, те в свою очередь — еще более маленькими башнями. И так до восьми (а порой и больше) уровней, представляющих различные аспекты индуистского мифологического пантеона.

Фракталы в архитектуре — не уникальное изобретение одной части света. Сложное убранство готической, ренессансной и барочной архитектуры, особенно выраженное в соборах, часто демонстрирует фрактальное копирование и масштабирование на нескольких уровнях. Характерное для европейской архитектуры с конца XII в. переплетение арок скорее имело не эстетическое, а практическое значение: оно было разработано для укрепления окон и стен против давления ветра.

С конца XX века фрактальную геометрию использовали осознанно для создания интересных и приятных глазу фасадов. На фото — здание одного из самых сложных в архитектурном плане комплексов, расположенное в мельбурнском городском районе (Австралия). В комплексе объединены культурные, рекреационные и коммерческие проекты.

Опасные фракталы

Большинство фрактальных изображений, генерируемых математическими, естественными и человеческими процессами, обладают общим эстетическим качеством, основанным на визуальной сложности. Участники тестов визуального восприятия предпочитают фракталы именно естественного происхождения с размерностью 1,3—1,5. Для примера: волны и облака имеют размерность 1,3, береговая линия — 1,05.

А что, если увеличить размерность? Получившийся объект не всегда будет приятно разглядывать. На иллюстрации выше изображена картина распределения электрического разряда с размерностью 1,75, известная как фигура Лихтенберга, созданная высоковольтным электрическим разрядом на непроводящем материале.

Еще один отталкивающий объект — фрактальный продукт кристаллических структур с размерностью 1,8, сфотографированный через микроскоп.

Демосцена & софт

Пожалуй, нигде так красочно не исследовали мир фракталов, как в демосцене. Hartverdrahtet — достойный победитель конкурса демосцены 2012 года по 4-килобайтным файлам. Автор, Demoscene Passivist, говорит, что для создания демо с процедурно генерируемыми фрактальными ландшафтами потребовалось около двух месяцев.

А вот один из лучших проектов с фрактальными эффектами в демосцене. К сожалению, качество демонстрационного видео крайне плохое (из-за давности лет), но демо можно скачать и запустить на компьютере.

Для создания подобных или других фрактальных миров особых ухищрений не требуется. Есть несколько отличных программ, с помощью которых вы сможете самостоятельно изучать особенности фрактальной вселенной.

XaoS Open Source Project. Бесплатный, открытый, кроссплатформенный инструмент для масштабирования и изучения множества Мандельброта и десятков других фракталов.

JWildfire. Еще одна кроссплатформенная (в том числе с мобильной версией) программа, основанная на Java с открытым исходным кодом, для обработки изображений. Она известна в основном своим сложным генератором пламенных фракталов.

Mandelbulber | Mandelbulb3D. Превосходные бесплатные инструменты для создания трехмерных фракталов, таких как устрашающая Оболочка Мандельброта, загадочная «коробка» Мандельбокс и др. Mandelbulber несколько более функционален и быстр, но Mandelbulb3D чуть проще в использовании.

По ссылке вы найдете множество других программ.

Источник

Что такое фракталы: бесконечность и красота математики

Подобным же образом устроена и кровеносная система: от артерий отходят артериолы, а от них — мельчайшие капилляры, по которым кислород поступает в органы и ткани. Посмотрим на космические снимки морского побережья: мы увидим заливы и полуострова; взглянем на него же, но с высоты птичьего полета: нам будут видны бухты и мысы; теперь представим себе, что мы стоим на пляже и смотрим себе под ноги: всегда найдутся камешки, которые дальше выдаются в воду, чем остальные. То есть береговая линия при увеличении масштаба остается похожей на саму себя. Это свойство объектов американский (правда, выросший во Франции) математик Бенуа Мандельброт назвал фрактальностью, а сами такие объекты — фракталами (от латинского fractus — изломанный).

Какие бывают фракталы?

Если посмотреть на множество фракталов, в них можно увидеть множество отличий. Эти отличия наблюдаются не только в форме фигур, из которых состоят фракталы, но и в самой форме представления этих множеств. Таким образом, различают геометрические, алгебраические и стохастические фракталы. Расскажем о каждом из них чуть подробнее.

Геометрические фракталы

Это самый привычный нам вид фракталов. Они строятся на основе какой-либо геометрической фигуры путем дробления ее частей и их преобразования. Среди примеров можно назвать L-системы. Изначально они были спроектированы для моделирования биологических клеточных систем, но с таким же успехом могут быть применены и к другим ветвящимся системам.

Алгебраические фракталы

Алгебраические фракталы строятся на основе математических формул — их можно превратить в геометрические, если построить графики на координатной плоскости. Среди алгебраических фракталов можно выделить фракталы Мандельброта, Жюлиа и бассейны Ньютона. Все они строятся на множестве комплексных чисел, которые состоят из действительной и мнимой части. Просто фракталы Мандельброта и Жюлиа строятся на основе квадратов комплексных чисел, а бассейны Ньютона — на основе их кубов.

Стохастические фракталы

Этот вид фракталов строится на основе математических формул, но в процессе построения параметры в них случайным образом изменяются. Это приводит к появлению причудливых форм, очень похожих на природные. В отличие от геометрических и некоторых алгебраических, стохастические фракталы можно построить лишь при помощи компьютера.

Геометрия и алгебра

Изучение фракталов на рубеже XIX и XX веков носило скорее эпизодический, нежели систематический характер, потому что раньше математики в основном изучали «хорошие» объекты, которые поддавались исследованию при помощи общих методов и теорий. В 1872 году немецкий математик Карл Вейерштрасс строит пример непрерывной функции, которая нигде не дифференцируема. Однако его построение было целиком абстрактно и трудно для восприятия. Поэтому в 1904 году швед Хельге фон Кох придумал непрерывную кривую, которая нигде не имеет касательной, причем ее довольно просто нарисовать. Оказалось, что она обладает свойствами фрактала. Один из вариантов этой кривой носит название «снежинка Коха».

Идеи самоподобия фигур подхватил француз Поль Пьер Леви, будущий наставник Бенуа Мандельброта. В 1938 году вышла его статья «Плоские и пространственные кривые и поверхности, состоящие из частей, подобных целому», в которой описан еще один фрактал — С-кривая Леви. Все эти вышеперечисленные фракталы можно условно отнести к одному классу конструктивных (геометрических) фракталов.

Другой класс — динамические (алгебраические) фракталы, к которым относится и множество Мандельброта. Первые исследования в этом направлении начались в начале XX века и связаны с именами французских математиков Гастона Жулиа и Пьера Фату. В 1918 году вышел почти двухсотстраничный мемуар Жулиа, посвященный итерациям комплексных рациональных функций, в котором описаны множества Жулиа — целое семейство фракталов, близко связанных с множеством Мандельброта. Этот труд был удостоен приза Французской академии, однако в нем не содержалось ни одной иллюстрации, так что оценить красоту открытых объектов было невозможно. Несмотря на то что это работа прославила Жулиа среди математиков того времени, о ней довольно быстро забыли. Вновь внимание к ней обратилось лишь полвека спустя с появлением компьютеров: именно они сделали видимыми богатство и красоту мира фракталов.

Как известно, размерность (число измерений) геометрической фигуры – это число координат, необходимых для определения положения лежащей на этой фигуре точки.
Например, положение точки на кривой определяется одной координатой, на поверхности (не обязательно плоскости) двумя координатами, в трёхмерном пространстве тремя координатами.
С более общей математической точки зрения, можно определить размерность таким образом: увеличение линейных размеров, скажем, в два раза, для одномерных (с топологической точки зрения) объектов (отрезок) приводит к увеличению размера (длины) в два раза, для двумерных (квадрат) такое же увеличение линейных размеров приводит к увеличению размера (площади) в 4 раза, для трехмерных (куб) – в 8 раз. То есть «реальную» (т.н. Хаусдорфову) размерность можно подсчитать в виде отношения логарифма увеличения «размера» объекта к логарифму увеличения его линейного размера. То есть для отрезка D=log(2)/log(2)=1, для плоскости D=log(4)/log(2)=2, для объема D=log(8)/log(2)=3.
Подсчитаем теперь размерность кривой Коха, для построения которой единичный отрезок делят на три равные части и заменяют средний интервал равносторонним треугольником без этого сегмента. При увеличении линейных размеров минимального отрезка в три раза длина кривой Коха возрастает в log(4)/log(3)

1,26. То есть размерность кривой Коха – дробная!

Наука и искусство

В 1982 году вышла книга Мандельброта «Фрактальная геометрия природы», в которой автор собрал и систематизировал практически всю имевшуюся на тот момент информацию о фракталах и в легкой и доступной манере изложил ее. Основной упор в своем изложении Мандельброт сделал не на тяжеловесные формулы и математические конструкции, а на геометрическую интуицию читателей. Благодаря иллюстрациям, полученным при помощи компьютера, и историческим байкам, которыми автор умело разбавил научную составляющую монографии, книга стала бестселлером, а фракталы стали известны широкой публике. Их успех среди нематематиков во многом обусловлен тем, что с помощью весьма простых конструкций и формул, которые способен понять и старшеклассник, получаются удивительные по сложности и красоте изображения. Когда персональные компьютеры стали достаточно мощными, появилось даже целое направление в искусстве — фрактальная живопись, причем заниматься ею мог практически любой владелец компьютера. Сейчас в интернете можно легко найти множество сайтов, посвященных этой теме.

Война и мир

Как уже отмечалось выше, один из природных объектов, имеющих фрактальные свойства, — это береговая линия. С ним, а точнее, с попыткой измерить его длину, связана одна интересная история, которая легла в основу научной статьи Мандельброта, а также описана в его книге «Фрактальная геометрия природы».

Речь идет об эксперименте, который поставил Льюис Ричардсон — весьма талантливый и эксцентричный математик, физик и метеоролог. Одним из направлений его исследований была попытка найти математическое описание причин и вероятности возникновения вооруженного конфликта между двумя странами. Казалось бы, при чем тут фракталы?

Но в числе параметров, которые учитывал ученый, была протяженность общей границы двух враждующих стран. Когда он собирал данные для численных экспериментов, то обнаружил, что в разных источниках данные об общей границе Испании и Португалии сильно отличаются. Это натолкнуло его на следующее открытие: длина границ страны зависит от линейки, которой мы их измеряем. Чем меньше масштаб, тем длиннее получается граница.Это происходит из-за того, что при большем увеличении становится возможным учитывать все новые и новые изгибы берега, которые раньше игнорировались из-за грубости измерений. И если при каждом увеличении масштаба будут открываться ранее не учтенные изгибы линий, то получится, что длина границ бесконечна! Прямо как математические фракталы. Правда, на самом деле этого не происходит — у точности наших измерений есть конечный предел. Этот парадокс называется эффектом Ричардсона.

Конструктивные (геометрические) фракталы

Алгоритм построения конструктивного фрактала в общем случае таков. Прежде всего нам нужны две подходящие геометрические фигуры, назовем их основой и фрагментом. На первом этапе изображается основа будущего фрактала. Затем некоторые ее части заменяются фрагментом, взятым в подходящем масштабе, — это первая итерация построения. Затем у полученной фигуры снова некоторые части меняются на фигуры, подобные фрагменту, Если продолжить этот процесс до бесконечности, то в пределе получится фрактал.

Рассмотрим этот процесс на примере кривой Коха. За основу кривой Коха можно взять любую кривую (для «снежинки Коха» это треугольник). Но мы ограничимся простейшим случаем — отрезком. Фрагмент — ломаная, изображенная сверху на рисунке. После первой итерации алгоритма в данном случае исходный отрезок совпадет с фрагментом, затем каждый из составляющих его отрезков сам заменится на ломаную, подобную фрагменту, На рисунке показаны первые четыре шага этого процесса.

Языком математики: динамические (алгебраические) фракталы

Таким образом, любая точка z комплексной плоскости имеет свой характер поведения при итерациях функции f (z), а вся плоскость делится на части. При этом точки, лежащие на границах этих частей, обладают таким свойством: при сколь угодно малом смещении характер их поведения резко меняется (такие точки называют точками бифуркации). Так вот, оказывается, что множества точек, имеющих один конкретный тип поведения, а также множества бифуркационных точек часто имеют фрактальные свойства. Это и есть множества Жулиа для функции f (z).

Варьируя основу и фрагмент, можно получить потрясающее разнообразие конструктивных фракталов.
Более того, подобные операции можно производить и в трехмерном пространстве. Примерами объемных фракталов могут служить «губка Менгера», «пирамида Серпинского» и другие.
К конструктивным фракталам относят и семейство драконов. Иногда их называют по имени первооткрывателей «драконами Хейвея-Хартера» (своей формой они напоминают китайских драконов). Существует несколько способов построения этой кривой. Самый простой и наглядный из них такой: нужно взять достаточно длинную полоску бумаги (чем тоньше бумага, тем лучше), и согнуть ее пополам. Затем снова согнуть ее вдвое в том же направлении, что и в первый раз. После нескольких повторений (обычно через пять-шесть складываний полоска становится слишком толстой, чтобы ее можно было аккуратно гнуть дальше) нужно разогнуть полоску обратно, причем стараться, чтобы в местах сгибов образовались углы в 90˚. Тогда в профиль получится кривая дракона. Разумеется, это будет лишь приближение, как и все наши попытки изобразить фрактальные объекты. Компьютер позволяет изобразить гораздо больше шагов этого процесса, и в результате получается очень красивая фигура.

Множество Мандельброта строится несколько иначе. Рассмотрим функцию fc (z) = z^2+с, где c — комплексное число. Построим последовательность этой функции с z0=0, в зависимости от параметра с она может расходиться к бесконечности или оставаться ограниченной. При этом все значения с, при которых эта последовательность ограничена, как раз и образуют множество Мандельброта. Оно было детально изучено самим Мандельбротом и другими математиками, которые открыли немало интересных свойств этого множества.

Источник