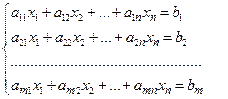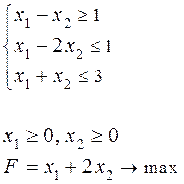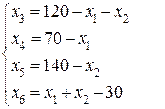к стандартной форме записи можно привести

Виды ЗЛП и способы перехода от одного вида к другому.

Одна и та же ЗЛП может быть сформулирована в различных эквивалентных формах. Наиболее важными формами задачи линейного программирования являются каноническая и стандартная.

К канонической форме можно преобразовать любую задачу линейного программирования.

Правило приведения ЗЛП к каноническому виду:

(32.1)

Тогда неравенство (32.1) запишется в виде:

В каждое из неравенств вводится своя “уравнивающая” переменная, после чего система ограничений становится системой уравнений.

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражаются расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в основной форме, равно объему неиспользуемого соответствующего ресурса.

2. Если в исходной задаче некоторая переменная не подчинена условию неотрицательности, то ее заменяют (в целевой функции и во всех ограничениях) разностью неотрицательных переменных

3. Если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1)

Таким образом, всякую задачу линейного программирования можно сформулировать в канонической форме.

В стандартной формезадача линейного программирования является задачей на максимум (минимум) линейной целевой функции. Система ограничений ее состоит из одних линейных неравенств типа « = »). Все переменные задачи неотрицательны.

Всякую задачу линейного программирования можно сформулировать в стандартной форме. Приведение к стандартной форме необходимо, таккакбольшинство методов решения задач линейного программирования разработано именно для стандартной формы.

Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:

— перейти от минимизации целевой функции к ее максимизации;

— изменить знаки правых частей ограничений;

— перейти от ограничений-равенств к неравенствам;

— избавиться от переменных, не имеющих ограничений на знак..

Примеры:

1. Привести к каноническому виду задачу

что и дает эквивалентную задачу в канонической форме.

2. Привести к стандартному виду задачу

Выразим через и остальные переменные:

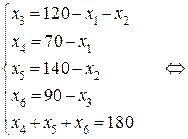
Целевая функция будет выглядеть следующим образом:

Или, после упрощения:

Так как , то перепишем нашу систему следующим образом: .

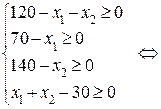
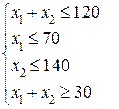
Итак, эквивалентная задача в стандартной форме будет выглядеть следующим образом:

Источник

Формы записи задачи линейного программирования

Задача линейного программирования записывается в различных формах. В одних задачах ограничения имеют вид равенств, в других случаях − в виде неравенств. Многие практические задачи сводятся к смешанным условиям, где часть ограничений неравенства, другие − равенства. Не во всех задачах требуется неотрицательность всех переменных. Такое разнообразие в формах записи требует разработки специальных методов для решения конкретных задач и затрудняет исследование общих особенностей линейного программирования и создания общих методов решения. Следовательно более удобно рассматривать способ сведения любой задачи линейного программирования к наиболее простой для исследования форме.

Каноническая форма задачи линейного программирования оказывается наиболее удобной при построении вычислительных алгоритмов. Для решения таких задач применяют симплекс метод.

Рассмотрим задачи линейного программирования записанные в различных формах.

Задача линейного программирования в форме

(1)

называется общей задачей линейного программирования.

Задача линейного программирования в форме

(2)

называется канонической задачей линейного программирования.

Задача линейного программирования в форме

(3)

(3′)

называется основной задачей линейного программирования или сопряженной канонической задачей линейного программирования.

Задача линейного программирования в форме

(4)

называется стандартной задачей линейного программирования.

Для приведения задачи линейного программирования к каноничнскому виду (2), нужно преобразовать неравенства в равенства добавлением в каждое неравенство дополнительного неотрицательного переменного. Если в ограничениях задачи линейного программирования есть переменные, на которых не налагается ограничения в виде неотрицательности, то это можно исправить заменив каждое такое переменное на

Источник

Приведение задач ЛП к стандартной форме

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися.

Для большинства методов решения задач ЛП требуется предварительно привести задачу к стандартной (канонической, нормальной) форме. Задача (или ее математическая модель) представлена в стандартной форме, если она соответствует следующим условиям:

· Целевая функция подлежит максимизации;

· Все ограничения имеют вид равенств;

· На все переменные накладываются ограничения неотрицательности.

Если целевая функция задачи подлежит минимизации, то для перехода к целевой функции, подлежащей максимизации, необходимо умножить исходную целевую функцию на (– 1). Доказано, что максимальное значение любой функции Е всегда равно минимальному значению функции (– Е), взятому с обратным знаком.

Если на какую-либо переменную накладывается ограничение неотрицательности, то она заменяется на разность двух переменных, каждая из которых должна быть неотрицательной. Таким образом, если некоторая переменная x_j по своему физическому смыслу может принимать как положительные, так и отрицательные значения, то во всех ограничениях и в целевой функции ее следует заменить на разность двух переменных: x ’ _j – x ” _j. На эти переменные накладываются ограничения неотрицательности: x ’ _j 0, x ” _j 0.

x₁ 0; x₂ 0

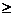
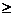
Здесь переменные x₃, x₄ – избыточные, x₅ – остаточная.

Примечание. Все переменные, которые вводятся в математическую модель для ее приведения к стандартной форме, имеют физический смысл. Так, в рассмотренном примере переменные x₃ и x₄ обозначают количество кислот, которое будет выпущено сверх государственного заказа. Переменная x₅ обозначает, насколько количество опасных отходов, образующихся при производстве кислот, будет меньше максимально допустимой величины (600 т).

Приведем к стандартной форме задачу из примера 1.2. В ней имеются три ограничения «больше или равно». В каждое из них необходимо ввести избыточную переменную. Целевая функция задачи подлежит минимизации, ее необходимо умножить на (– 1), чтобы перейти к целевой функции, подлежащей максимизации. Математическая модель задачи в стандартной форме будет иметь следующий вид:

x₁ 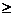0; x₂ 0

Источник

Симплексный метод решения задач линейного программирования

Симплексный метод решения задач линейного программирования

Введение

Общая постановка задачи

а) Если система ограничений ЗЛП обладает хотя бы одним решением, она называется совместной в противном случае несовместной; б) Допустимое множество решений ЗЛП не пусто, если система ограничений совместна; в) Множество допустимых решений ЗЛП (если оно не пусто) в общем случае является многогранным множеством. Линейная функция Q(X ) называется функцией цели, целевой функцией (ЦФ), множество планов <X > удовлетворяющих системе ограничений (2) – (5), ­­- множеством допустимых решений (альтернатив) и обозначается символом R, X є Ω Допустимый план X є Ω, доставляющий целевой функции (1) экстремальное значение, называется оптимальным. Задача в форме (1) – (5) представляет общую задачу линейного программирования.

Cтандартная форма задачи

Если все ограничения задачи заданы в виде строгих равенств и на переменные величины наложено условие неотрицатаельности x_j ≥0, j = 1(1)n, то такую формулировку называют стандартной:

Экстремумы функций в общем случае связаны простыми соотношениями

Переход от общей задачи к стандартной

Каноническая форма задачи

Удобство этой формы ЗЛП состоит в том, что она позволяет предельно просто получить первое допустимое решение. Для этой формы должны быть выполнены условия:

правые части в ограничениях – неотрицательны b_i ≥ 0, i = 1(1)m;

каждое уравнение содержит переменную x_j ≥0 с коэффициентом при ней равным “1” в этом уравнении и с коэффициентом “0” во всех других уравнениях; эти переменные называют дополнительными или искусственными;

в ЦФ эти переменные входят с коэффициентом “0”;

определение опорного плана (начальной вершины) выполняют методом искусственного базиса, что ещё до решения задачи позволяет выяснить факт существования решения.

Если исходная задача имеет хотя бы один план, то расширенная задача (после введения искусственных переменных в систему ограничений) также содержит этот план в качестве своего допустимого решения

Геометрическая интерпретация ЗЛП

Выпишем их и присвоим им имена

Целевая функция. Что можно сказать о линейной форме (ЦФ)? Это функция двух переменных x₁ и x2, её образ в трёхмерном пространстве – плоскость, проходящая через начало координат. Найдём частные производные ЦФ по х_j

Таким образом, перемещаясь вдоль вектора C или по прямой х₂ =с₂х₁/c₁, легко построить линию уровня (она перпендикулярна х₂ = с₂х₁/c₁ ) и вычислить значение ЦФ Q для этой линии. Экстремум Q, очевидно, будет достигаться в положении касания линией уровня (её проекцией) границы множества допустимых решений. Такое касание может быть трёх типов: в вершине, по ребру, по грани многогранника. Этим типам касания соответствуют: единственное решение в вершине и бесконечное множество решений в других случаях. Область допустимых решений. Рассмотрим случаи ограниченной и неограниченной области допустимых решений. В последнем случае поиск экстремума Q может приводить к отсутствию решения, так как extr Q → ±∞ или существует опорная прямая линия, касающаяся неограниченного многогранника, и тогда решение существует.

Пример. Описание области допустимых решений.

Мы можем записать уравнение границы области D заданной неравенствами:

Теорема 1. Любой вектор n-мерного векторного пространства можно представить, как линейную комбинацию векторов базиса, притом единственным образом. Определение 2.5. Максимальное число линейно независимых векторов линейного пространства называется размерностью линейного пространства. Линейное пространство обычно обозначают, R_n где n – его размерность. Выпуклой оболочкой точек называется множество всевозможных выпуклых комбинаций этих точек. Множество называется выпуклым, если вместе с двумя любыми его точками оно содержит и их произвольную выпуклую линейную комбинацию. С геометрической точки зрения это означает, что выпуклое множество содержит вместе с любыми двумя своими точками и соединяющий их отрезок. Выпуклое множество совпадает со своей выпуклой оболочкой. Примерами выпуклых множеств являются прямолинейный отрезок, квадрат, круг, прямая, полуплоскость, куб, шар, полупространство и другие. Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой линейной комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, угловыми точками круга – точки окружности. Таким образом, выпуклое множество может иметь конечное или бесконечное число угловых точек, но может не иметь их совсем. Например, прямая, плоскость, полуплоскость, пространство, полупространство угловых точек не имеют. Одним из основных понятий теории линейного программирования является понятие выпуклого многогранника в n-мерном пространстве, частными случаями которого являются при n = 1 отрезок на прямой, при n = 2 выпуклый многоугольник на плоскости. Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество точек на плоскости, имеющее конечное число угловых точек, называемых вершинами. Прямолинейные отрезки, соединяющие две вершины и образующие границу, называются сторонами многоугольника.

Опорной прямой выпуклого многоугольника называется прямая, имеющая с многоугольником, расположенным по одну сторону от нее, хотя бы одну общую точку.

Выпуклым многогранником называется выпуклое замкнутое ограниченное множество точек пространства, имеющее конечное число угловых точек, называемых его вершинами. Многоугольники, ограничивающие многогранник, называются его гранями, а отрезки, по которым пересекаются грани, называются ребрами. Опорной плоскостью многогранника называется плоскость, имеющая с многогранником, расположенным по одну сторону от нее, хотя бы одну общую точку.

Теорема 2.2. Выпуклый n-мерный многогранник является выпуклой линейной комбинацией своих угловых точек.

Следствие 2.3. Из теоремы вытекает, что выпуклый многогранник порождается своими угловыми точками (вершинами): отрезок – двумя точками, треугольник – тремя точками, n – угольник на плоскости – n точками и т. д. В тоже время выпуклая многогранная область, содержащая бесконечно удаленную точку, являясь неограниченным множеством, не определяется однозначно своими угловыми точками: любую ее точку нельзя представить в виде выпуклой линейной комбинации угловых точек.

Элементы выпуклых множеств

Определение 1. Множеством называется совокупность элементов любой природы, для которых задано правило принадлежности к данному множеству.

Определение 7. Множество М называется в ы п у к л ы м, если вместе с любыми двумя точками, принадлежащими данному множеству, оно содержит и отрезок их соединяющий. В общей форме ЗЛП каждый символ R1, R2, …, Rm означает один из знаков: = или ≠. В такой форме задачи линейного программирования часть переменных может быть подчинена условию неотрицательности (x_i ≥ 0), часть – условию неположительности (x_j ≤ 0), а какие-то переменные, возможно, могут принимать любые значения.

Общий алгоритм симплексного метода ЗЛП

Пусть система невырожденна и совместна, т.е. r_A = r_B = r = m

Все введённые переменные в новых обозначениях удобно свести в таблицу, которая называется симплексной.

Алгоритм решения

1) Формируем исходный план при свободных переменных; x_j =0, j = m+1(1)n, x_j = β_ф, ф = 1(1)m при β_ф > 0 план x o допустим Q(x) =x_o.

2) Проверяем этот план на оптимальность, используя значения γ_j коэффициентов ЦФ в последней строке таблицы. Могут быть два случая:

б) некоторые γ_j > 0. В этом случае увеличение значений соответствующих свободных переменных x_j (γ_j > 0) будет минимизировать Q, так как

Чтобы Q уменьшалось, такие переменные следует вводить (последовательно) в базис, но, чтобы размерность пространства не изменялась из базиса должны выводиться переменные в число свободных (по одной) формируем множество индексов Г = < j | γ_j >0>. Какая переменная должна первой вводиться в базис? Вообще последовательно перебирая (вершины симплекса) решение отыскивается при произвольном выборе, но для определённости выбираем новую базисную переменную с индексом v = argmax <x_j>, где j ∈ Г. Теперь определим переменную (базисную), которая будет выводиться из базиса.

В системе уравнений

Начинаем увеличивать х_v до тех пор, пока некоторый х_ф станет отрицательным. Первый же х_ф ≤ 0 будет выводиться из базиса. Определение. Столбец с индексом v и строка с индексом ф = i называются направляющими.

3) Проверка существования решения (ограниченность ЗЛП). В выражениях, связывающих х, ∝, β, х_ф = β_ф -∝_фvх_v, ф=1(1)m, могут быть все ∝_фv 0. Пусть ЦФ ограничена и некоторые ∝_фv > 0. Сформируем множество индексов S = < ф | ∝_фv >0>. Из базиса необходимо выводить переменную с индексом i, так как она первая обращается в нуль, i = argmin(β_ф/∝_фv), где ф∈S, таким образом, базисная переменная x_i выводится из базиса.

4) Формируем новые множества:

Дальнейшие действия алгоритма:

преобразуем задачу, т.е. все базисные переменные и целевую функцию выражаем через свободные переменные;

заполняем новую симплексную таблицу;

делаем все свободные переменные х_j = 0 и находим опорный план;

Опорный план (вектор) такой Х’ = ; Q(Х’ ) ≤ Q₀ ;

если план не оптимален, то определяем направляющий столбец;

проверяем существует ли оптимальный план;

если оптимальный план существует, то находим направляющую строку и вновь изменяем базис и т. д.

Переход от одной таблицы к другой связан с трудоемкими расчетами (о чем надо еще написать) Вводимую в базис переменную х_ν (икс ню) выражаем через свободные переменные и выводимую х_i. Действуем так.

При ручном счете все эти действия проще выполнять с использованием вспомогательных таблиц по правилам специального алгоритма. Эти таблицы имеют прежнюю структуру, но клетки делятся на две полуклетки. В верхней полуклетке оставляем содержимое из прежней таблицы.

При решении задач линейного программирования вычисляются ранги у матрицы ограничений и расширенной матрицы ранги должны быть равны r=m.

Матрица и её ранг. Система mn чисел, расположенных в форме прямоугольной таблицы из m строк и n столбцов, называется матрицей.

Определение. Минором k-го порядка матрицы [A] (k ≤ m, k ≤ n) называется определитель D, составленный (с сохранением порядка) из k 2 элементов матрицы, лежащих на пересечении некоторых её k столбцов и k строк См. схему выше минор D из 3-х строк и 3-х столбцов. Обозначается матрица символами:

Матрица А и ее миноры с различным окаймлением

Приведем пример вычисления ранга матрицы.

С выполнением каждого шага связаны процедуры:

1. Получение опорного плана; 2. устанавливается, является ли данный опорный план оптимальным; 3. если нет, то существует ли оптимальный план вообще, или задача является неограниченной; 4. если оптимальный план существует, то, как перейти на следующем шаге, к новому опорному плану с меньшим значением ЦФ.

Алгоритм СМ применяется к ЗЛП после её приведения к канонической форме, т.е. отыскивается минимум целевой функции min Q(X) на множестве векторов Х .

(здесь x_e, e =(m+1)(1)n). Матрица этой системы неособенная и, следовательно, система имеет единственное решение x_j , j =1(1)m.

Исходный опорный план ЗЛП – вектор, содержащий значения всех переменных задачи как базисных, так и свободных, т.е. этот вектор Х , удовлетворяет ограничениям, но не обеспечивает, как правило, экстремума ЦФ. Общее число опорных планов очевидно равно числу сочетаний из n по m. Оптимальный план можно выявить, перебрав их все. Такой путь громоздок и неприемлем уже при n, m ≈ 10 ÷15.

Алгоритм СМ тоже перебирает опорные планы, но не все, а направленно, т.е. на каждом шаге ЦФ уменьшается. Число шагов имеет тот же порядок, что и число уравнений в ограничениях.

Приведем пояснения некоторым понятиям и терминам, широко используемым в алгоритме решения задач линейного программирования симплексным методом и тесно связанными с ним методами.

Определение. Системой линейных уравнений называют систему следующего вида. Ранг матрицы определяется через миноры r = – 5.

Определение. Симплекс – выпуклый многоугольник в n-мерном пространстве с n + 1 вершинами, не лежащими в одной гиперплоскости. Симплексы выделены в отдельный класс потому, что в n-мерном пространстве n точек всегда лежат в одной гиперплоскости. Другими словами, симплекс – это простейший многоугольник, содержащий некоторый объем n-мерного пространства. В обычном (трехмерном) пространстве симплекс – это тетраэдр; трехмерный объем совпадает с объемом тела. На плоскости симплекс – это треугольник, двумерный объем – площадь; на прямой – симплекс – отрезок, объем – длина отрезка.

Определение. Гиперпространство, гиперплоскость. Гиперпространство многомерного (n-мерного) пространства – это его подпространство размерности (n – 1). Главное свойство гиперпространства – то, что оно «самое большое» подпространство. Иначе говоря, если к базису выбранного гиперпространства добавить еще один линейно независимый вектор, то можно получить базис всего пространства.

Например, для трехмерного пространства гиперпространством является плоскость (любая), проходящая через начало координат. Для двумерного пространства – гиперпространство – это прямая линия, проходящая через нуль.

Гиперплоскость в n-мерном пространстве обобщает наши представления о роли прямой на плоскости и плоскости в пространстве. Например, в n-мерном пространстве через любые n точек можно провести единственную гиперплоскость (как в трехмерном через три точки общего положения, т.е. не лежащие на одной прямой).

Гиперплоскость определяется линейной формой: а₁х₁ + а₂х₂ + … + а_nx_n = k, где коэффициенты (а₁, а₂, …, а_n) представляют собой координаты вектора А.

Гиперплоскость делит пространство (соответствующей размерности) на два полупространства. Все точки каждого из них определяются неравенствами. Например, в случае прямой линии на плоскости: а₁х₁ + а₂х₂ ≥_Z, или а₁х₁ + а₂х₂ >Z _, а₁х₁ + а₂х₂ Литература

Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.

Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.

Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.

Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.

Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.

Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.

Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.

Источник