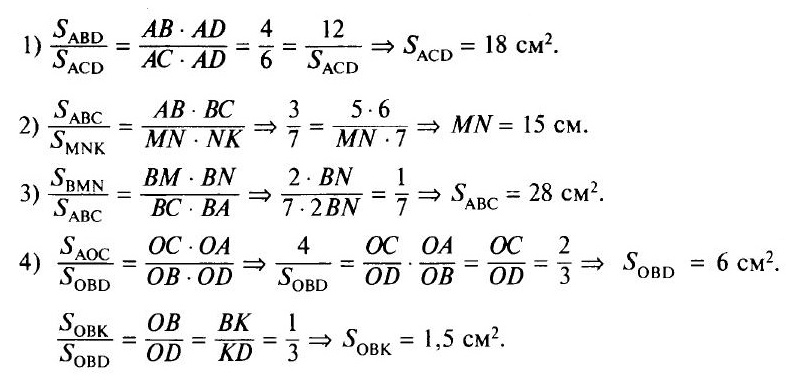как найти отношение площадей подобных треугольников

Отношение площадей подобных треугольников – определение

Знание признаков подобия треугольников и умение эти признаки использовать открывает новые пути в решениях задач. Иногда ученики встают в ступор при необходимости определения отношения площадей подобных треугольников из-за новизны подхода к выводу формулы. Рассмотрим сам вывод для того, чтобы понять принцип и использовать его в дальнейшем для решения задач.

Подобие

Подобными треугольниками называются треугольники, все стороны которых пропорциональны друг другу. Отношение соответствующих сторон в подобных треугольниках всегда равняется одному и тому же числу, которое называется коэффициентом подобия.

Рис. 1. Подобные треугольники

Коэффициент подобия часто используется для решения задач на подобные треугольники, ведь можно через одно отношение найти коэффициент, после выразить неизвестную сторону через известную. Коэффициент подобия обозначают буквой k.

Не нужно зацикливаться только на треугольниках. Хотя признаки подобия выведены только для них, любая фигура в геометрии имеет подобную. То же касается и равенства фигур: любая фигура в геометрии имеет равную себе, ведь равенство это частный случай подобия с коэффициентом k=1

Рис. 2. Подобные фигуры

Признаки подобия

На сегодняшний день для произвольного треугольника существует 3 признака подобия.

Рис. 3. Признаки подобия треугольников

Для того, чтобы доказать пропорциональность сторон нужно посчитать отношение соответствующих сторон. У пропорциональных сторон результаты получатся одинаковыми.

У пропорциональны треугольников будут так же пропорциональны и все характеризующие отрезки: высота, медиана, биссектриса. Коэффициент подобия одинаков для всех отрезков треугольника. Этот факт нужно запомнить, он важен для решения многих задач и выведения формулы отношения площадей подобных треугольников.

Площади подобных треугольников

$$S=<1over<2>>h*AB$$, тогда площадь второго треугольника:

Если поделить одну площадь на вторую, то получится следующее отношение:

$$>=<over>$$ если вспомнить, что отношение сторон подобных треугольников равняется коэффициенту подобия, то получится следующий результат:

$$>=k*k=k^2$$ – то есть площади подобных треугольников относятся друг к другу с коэффициентом пропорциональности, равным коэффициенту подобия в квадрате

Что мы узнали?

Мы вспомнили, что такое подобные фигуры. Поговорили о подобных треугольниках. Выделили три признака подобия треугольников. Выяснили, что коэффициент подобия можно использовать не только для работы со сторонами треугольников, но и для любых характеризующих отрезков. Вывели формулу отношения площадей подобных треугольников.

Источник

Геометрия. 8 класс

Отношением отрезков AB и CD называется отношение их длин. Отрезки AB и CD пропорциональны отрезкам A₁B₁ и C₁D₁, если их отношения равны.
AB/(A₁B₁) = CD/(C₁D₁)
Выясним, пропорциональны ли отрезки на рисунке.

Составим отношения отрезков, учитывая их длины:
AB/AC = 4/12 = 1/3,
AD/DE = 3/9 = 1/3,
DB/BE = 1/5,
Получим, что отрезки AB и AC пропорциональны отрезкам AD и DE. А отрезки AB и AC не пропорциональны отрезкам DB и BE.
Интересное и важное свойство биссектрисы угла треугольника связано с пропорциональностью отрезков.
Пусть дан треугольник АВС, в нем проведена биссектриса АD, докажем, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Дано: ∆ ABC, AD – биссектриса
Доказать: BD/AB = DC/AC
Для доказательства воспользуемся следствиями из формулы площади треугольника:
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

У треугольников ADC и ABD общая высота AH, поэтому
S_ABD/S_ADC = BD/DC
2) У треугольников ADC и ABD
∠CAD = ∠BAD, поэтому
S_ABD/S_ADC = (AB ∙ AD)/(AC ∙ AD) = AB/AC
3) BD/DC = AB/AC
Или
BD/AB = DC/AC
В геометрии фигуры одинаковой формы называют подобными.
Рассмотрим два треугольника, углы которых равны.
∆ ABC и ∆A₁B₁C₁
∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁
Тогда стороны AB и A₁B₁, BC и B₁C₁, CA и C₁A₁ называются сходственными.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
∆ ABC

Источник

Как найти отношение площадей подобных треугольников

Два треугольника подобны:

Из признаков подобия следует утверждения, которые удобно использовать в решении задач:

1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.

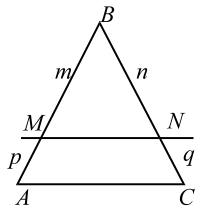Рис. 5

3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)

$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$

$$1.\;\left.\beginBC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm<по>\;\mathrm<двум>\;\mathrm<углам>)\end\right|\Rightarrow\dfrac ba=\dfrac pq$$ (1)

$$2.\;\left.\beginMO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end\right|\Rightarrow\dfrac xa=\dfrac p$$. (2)

Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.

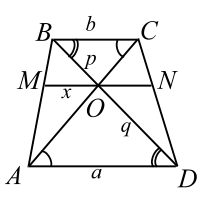Рис. 6

Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.

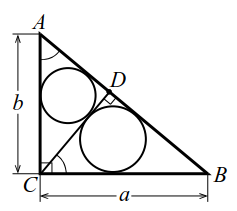Рис. 7

Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.

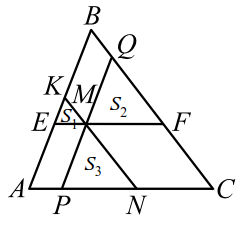Рис. 8

Свойства медиан, высот, биссектрис треугольника

В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.

Рис. 9

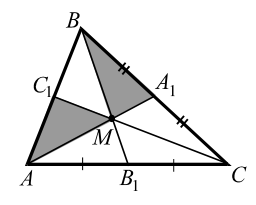
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.

Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.

Рис. 10

2. Площадь треугольника находим по формуле Герона:

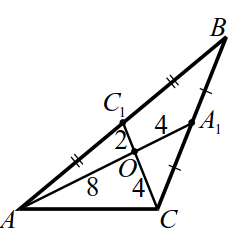
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Были доказаны также две леммы о высотах

1-ая лемма.

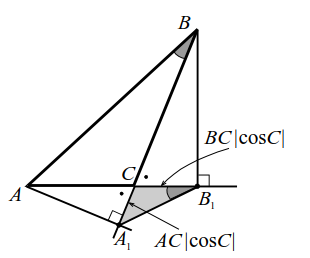Рис. 11a	Рис. 11б

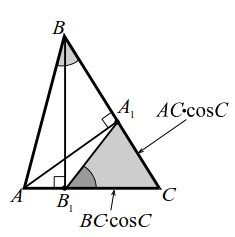
2-ая лемма.

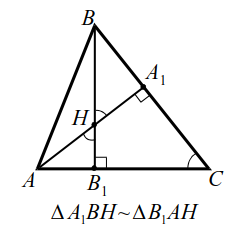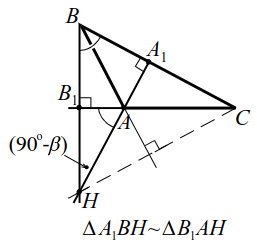Рис. 12a	Рис. 12б

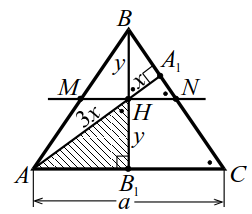Рис. 13

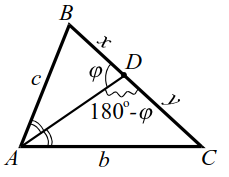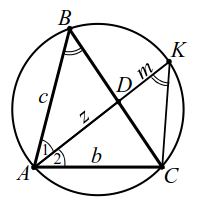Рис. 14	Рис. 14а

Источник

Подобные треугольники. Отношение периметров подобных треугольников. Коэффициент подобия

Что такое подобные треугольники?

Подобные треугольники определение

Подобные треугольники определение:

На рисунке изображены два подобных треугольника, у них углы соответственно равны, т.е. угол A равен углу A₁, угол B равен углу B₁, угол C равен углу C₁.

Сходственные стороны треугольников

Сходственные стороны треугольников пропорциональны:

здесь k называется коэффициентом подобия.

Отношение площадей подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия:

Отношение периметров подобных треугольников

Отношение периметров подобных треугольников:

Докажем это утверждение. Пусть имеются два подобных треугольника ABC и A₁B₁C₁. По определению подобных треугольников их сходственные стороны пропорциональны:

Периметр треугольника ABC равен сумме длин его трёх сторон:

Сумма в скобках в правой части равенства представляет собой периметр треугольника A₁B₁C₁. Разделим обе части равенства на периметр A₁B₁ + B₁C₁ + A₁C₁. Получаем:

что и требовалось доказать. Итак, отношение периметров подобных треугольников равно коэффициенту подобия.

Для установления факта подобия двух треугольников используют признаки подобия треугольников:

Источник

Как найти отношение площадей подобных треугольников

Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников. Вернуться к Списку уроков Тематического планирования.

Урок 32. Отношение площадей
подобных треугольников

Основные дидактические цели урока: закрепить понятия пропорциональных отрезков и подобных треугольников; совершенствовать навыки решения задач на применение свойства биссектрисы треугольника и определения подобных треугольников; рассмотреть теорему об отношении площадей подобных треугольников и показать ее применение в процессе решения задач.

Ход урока

I. Организационный момент

(Учитель сообщает тему урока, формулирует цели урока.)

II. Актуализация знаний учащихся. Мотивация к учебной деятельности

1. Теоретический опрос.

(Один ученик оформляет доказательство теоремы на доске.)
1) Ответить на вопросы 1—3 учебника.
2) Доказать свойство биссектрисы треугольника.

2. Проверка домашнего задания.

(Учитель проверяет решение задач № 538, 542. Два ученика готовят решение на доске.)

Задача № 538

Задача № 542

3. Работа по индивидуальным карточкам.

(3—6 учеников работают по карточкам.)

I уровень сложности

II уровень сложности

III уровень сложности

Ответы и указания к задачам по готовым чертежам:

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:

III. Работа по теме урока

(Учитель делит класс на группы для решения задания творческого характера. После завершения работы заслушиваются и обсуждаются варианты решений.)

Задание. Треугольники АВС и А1В1С1 подобны с коэффициентом подобия k. Найти отношение их площадей.

Вывод. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

IV. Закрепление изученного материала

Задача № 545

Вопросы для обсуждения.

V. Самостоятельная работа

I уровень сложности

II уровень сложности

III уровень сложности

VI. Рефлексия учебной деятельности

Домашнее задание

I уровень сложности: В подобных треугольниках АВС и KMN равны углы В и М, С и N, АС = 3 см, KN = 6 см, MN = 4 см, ∠AX = 30°. Найдите ВС, ∠K; отношение площадей треугольников AВС и KMN; АЕ и BE, если известно, что СЕ — биссектриса треугольника АВС, АВ = 3,5 см.

II уровень сложности: В прямоугольном треугольнике ABC ∠C = 90°, ∠B = 30°, АВ = 12 см, CD — высота. Докажите, что ΔACD подобен ΔАВС, найдите отношение их площадей и отрезки, на которые биссектриса угла А делит катет ВС.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников.

Источник