как найти точку приложения равнодействующей силы
Учебники
Журнал «Квант»
Общие
Кикоин А.К. Когда к телу приложены параллельные силы //Квант. — 1985. — № 2. — С. 23-25.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Содержание
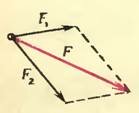
Хорошо известно, как найти равнодействующую двух сил, приложенных к материальной точке (рис. 1). На векторах, изображающих эти силы, как на сторонах строят параллелограмм; диагональ со стрелкой на конце, проведенная из точки, к которой приложены силы, и есть вектор равнодействующей.
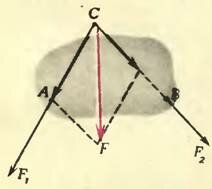
Когда две силы приложены не к материальной точке, а к телу, но так, как показано на рисунке 2, то равнодействующая определяется таким же образом. Пользуясь тем, что точку приложения силы можно переносить вдоль линии ее действия («Физика 8», § 46), находят точку С, в которой пересекаются линии действия обеих сил.
\vec F_2\) приложены именно к этой точке, строят параллелограмм и проводят диагональ. Правда, точка С может оказаться и вне тела, но тогда точку приложения равнодействующей можно выбрать в любом месте на линии ее действия. Действительно, какую бы точку мы не выбрали, равнодействующая сила \(
\vec F\) сообщит телу такое же ускорение или вызовет такой же вращающий момент, как и силы \(
\vec F_2\), вместе взятые.
Если силы параллельны и направлены в одну сторону
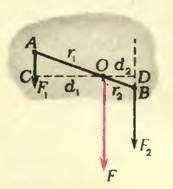
Пусть к телу приложены две параллельные сонаправленные силы (рис. 3). Линии действия таких сил нигде не пересекаются, и параллелограмм на них построить нельзя. Тем не менее сложить эти силы и найти их равнодействующую можно.
Нетрудно понять, что равнодействующая направлена параллельно обеим силам и ее модуль равен арифметической сумме модулей складываемых сил. А в какой точке она приложена? Или, другими словами, к какой точке тела надо приложить силу, равную по модулю, но противоположную по направлению равнодействующей, чтобы тело находилось в равновесии?
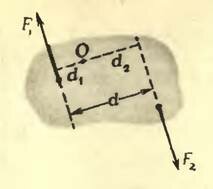
Чтобы найти точку приложения равнодействующей двух параллельных и одинаково направленных сил, можно воспользоваться правилом моментов («Физика 8», § 48). Проведем прямую, соединяющую точки А и В (см. рис. 3). Где-то на этой прямой должна, очевидно, находиться и точка приложения равнодействующей. Пусть это будет точка О. Допустим, что через эту точку проходит закрепленная ось, перпендикулярная плоскости, содержащей обе складываемые силы (то есть перпендикулярная плоскости рисунка). Если О действительно есть точка приложения равнодействующей, то тело будет находиться в равновесии — равнодействующая уравновешивается силой реакции со стороны оси. С другой стороны, если тело с закрепленной осью находится в равновесии, то алгебраическая сумма моментов сил относительно этой оси должна быть равна нулю. Из рисунка 3 видно, что сила \(
\vec F_2\), будь она единственной, поворачивала бы тело вокруг О по часовой стрелке, то есть ее момент F2d2 положительный, а сила \(
\vec F_1\) если бы она была единственной, поворачивала бы тело против часовой стрелки — ее моменту F1d1 надо приписать отрицательный знак (здесь d1 и d2 — плечи сил \(
Из подобия треугольников АОС и BOD находим, что \(
Это значит, что равнодействующая двух параллельных, одинаково направленных сил приложена к точке, делящей отрезок, соединяющий точки приложения складываемых сил, в отношении, обратном отношению модулей сил. Ясно, что эта точка лежит ближе к большей из сил.
Если направления параллельных сил противоположны
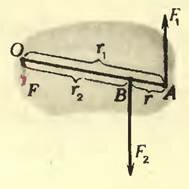
Приложенные к телу параллельные силы могут быть направлены и в противоположные стороны (рис. 4). Теперь точка приложения равнодействующей \(
\vec F\) не может находиться где-то между точками приложения сил \(
\vec F_2\). Ведь вокруг любой точки, лежащей между ними, каждая сила поворачивает тело против часовой стрелки, знаки моментов этих сил одинаковы, и их сумма не может быть равна нулю, как это требуется для равновесия.
Легко догадаться, что точка приложения равнодействующей лежит за точкой приложения большей силы, как это и показано на рисунке 4. Модуль же равнодействующей равен модулю разности модулей сил \(
\vec F_2\). В какой же именно точке приложена равнодействующая? На каком расстоянии r2 от точки приложения большей силы? Воспользуемся опять правилом моментов:
Вычтем из правой и левой частей последнего равенства величину F1:
Таким образом, точка приложения равнодействующей двух противоположно направленных параллельных сил расположена тем дальше от точки приложения большей из них, чем меньше разность модулей этих сил.
Пара сил
Мы видели, что если к телу приложены параллельные силы, одинаково или противоположно направленные, то всегда можно найти модуль и направление равнодействующей этих сил и определить точку ее приложения. Если к этой точке приложить силу, равную равнодействующей по модулю, но противоположную ей по направлению, то тело будет находиться в равновесии — оно не будет двигаться поступательно и не будет вращаться.
Но, оказывается, есть один случай, когда равнодействующую найти нельзя. Так бывает, если к телу приложены две параллельные, противоположно направленные силы, по модулю равные друг другу. Про такие силы говорят, что они образуют пару сил. Модуль их равнодействующей равен, конечно, нулю, а из формулы (*) видно, что при F2 — F1 =0 расстояние r2 до точки приложения равнодействующей равно бесконечности, то есть что такой точки попросту не существует. И в самом деле, какая же может быть точка приложения равнодействующей, которой нет?
Достаточно, однако, взглянуть на рисунок 5, чтобы понять, что под действием пары сил тело не будет находиться в равновесии — оно будет вращаться. Значит, у пары сил есть некоторый вращающий момент. Но относительно какой оси?
Нетрудно показать, что суммарный момент сил, составляющих пару, одинаков для любой оси, перпендикулярной плоскости, в которой лежат обе эти силы (перпендикулярной плоскости рисунка). Действительно, возьмем любую точку О и проведем через нее ось вращения. Момент M1 силы \(
\vec F_2\) относительно этой же оси равен F2d2. Суммарный момент М обеих сил равен M1 + M2 :
где d — расстояние между линиями действия сил, составляющих пару, называемое плечом пары сил. Значит, момент пары сил равен произведению модуля одной из сил на плечо пары. Так и говорят — момент пары сил — и не указывают относительно какой оси.
Как же все-таки «ведет» себя тело, к которому приложена пара сил? Чтобы ответить на этот вопрос, вспомним, что центр масс тела (о нем говорится в § 44 «Физики 8») движется так, как будто в нем сосредоточена вся масса тела и к нему приложены все действующие на тело силы (это утверждение называется в физике теоремой о движении центра масс). Но если сумма сил равна нулю, то центр масс не может тронуться с места (если, конечно, он покоился до приложения сил). Когда на тело действует пара сил, сумма сил как раз и равна нулю, и она не может привести в движение центр масс. Тело, однако, вращается. Значит, вращается оно вокруг оси, проходящей через центр масс (ведь все точки на оси вращения находятся в покое). Оси вращения, проходящие через центры масс тел, тем и замечательны, что на них не действуют никакие силы.
Лекция 7. Параллельные силы. Распределенная нагрузка
7.1. Сложение двух сонаправленных сил
Рассмотрим твердое тело, к точкам A1 и A2 которого приложены сонаправленные силы \(\vec F_<1>\) и \(\vec F_<2>\) (рис. 7.1 а). Если бы они были равны по модулю и перпендикулярны отрезку A1A2, то из соображений симметрии можно было бы заключить, что у них имеется равнодействующая \(\vec R\), приложенная в середине отрезка, сонаправленная с обеими силами и по модулю превосходящая каждую из них вдвое (рис. 7.1 б). Возникает вопрос: существует ли равнодействующая в общем случае, изображенном на рис. 7.1 а)?
Замечание. В нарушении симметрии роль играет лишь неравенство модулей сил, но не угол, образуемый векторами \(\vec F_<1>\), \(\vec F_<2>\) и отрезком A1A2. Например, силу \(\vec F_<2>\) можно перенести вдоль ее линии действия в некоторую точку B так, что новый отрезок A1B будет перпендикулярен этой силе.
Покажем, что и в общем случае у двух сонаправленных сил есть равнодействующая Для этого представим каждую из исходных сил \(\vec F_<1>\), \(\vec F_<2>\) в виде суммы двух новых сил: \(\vec F_<1>=\vec P_<1>+\vec Q_<1>\), \(\vec F_<2>=\vec P_<2>+\vec Q_<2>\). При этом потребуем, чтобы \(\vec P_<1>\) и \(\vec P_<2>\) были равны по модулю, противоположны по направлению и имели общую линию действия – A1A2 (рис. 7.2 а).
Рис. 7.2. Сложение двух сонаправленных сил
Согласно первой аксиоме статики, \(\vec P_<1>\) и \(\vec P_<2>\) уравновешивают друг друга. Поэтому исходная система \(\vec F_<1>,\vec F_<2>\) эквивалентна двум силам \(\vec Q_<1>,\vec Q_<2>\). Очевидно, что они непараллельны и лежат в той же плоскости, что и \(\vec F_<1>,\vec F_<2>\). Следовательно, их линии действия пересекаются в некоторой точке B этой же плоскости. Отложив силы \(\vec Q_<1>,\vec Q_<2>\) от этой точки и сложив по правилу параллелограмма, их можно заменить равнодействующей \(\vec R\).
Поскольку \(\vec P_<1>,\vec P_<2>\) уравновешивают друг друга, их также можно отложить от точки B. Это значит, что в B оказываются приложены силы \(\vec F_<1>=\vec P_<1>+\vec Q_<1>\) и \(\vec F_<2>=\vec P_<2>+\vec Q_<2>\). Поэтому равнодействующая \(\vec R\) равна \(\vec F_<1>+\vec F_<2>\): она сонаправлена с исходными силами, а по модулю равна их сумме.
Определим точку C, в которой линия действия \(\vec R\) пересекает отрезок A1A2. Треугольники, составленные из сил \(\vec F_<1>,\vec P_<1>,\vec Q_<1>\) и \(\vec F_<2>,\vec P_<2>,\vec Q_<2>\), подобны треугольникам BCA1 и BCA2, соответственно, поскольку их стороны параллельны (см. рис. 7.2 б). Поэтому
| $$\frac | (7.1) |
| $$F_<1>\cdot A_<1>C=F_<2>\cdot A_<2>C,\;\frac | (7.2) |
Найденную формулу можно сравнить с соотношением (5.2), выражающим правило рычага: чем больше сила F1, тем ближе к точке ее приложения должна находиться точка C. Такая аналогия не случайна. Действительно, если у сил \(\vec F_<1>,\vec F_<2>\) есть равнодействующая \(\vec R\), то имеется и уравновешивающая \(\vec R’\), которую можно считать приложенной в той же точке C (рис. 7.3).
Рис. 7.3. Аналогии с правилом рычага
Система \(\vec F_<1>,\vec F_<2>,\vec R’\) является уравновешенной. Из уравнений (4.3) следует, что сумма моментов этих сил относительно точки C равна нулю, т.е. F1d1 – F1d2 = 0. Но d1 = A1C cos α, d2 = A2C cos α, где α – угол между A1A2 и общим перпендикуляром к линиям действия сил \(\vec F_<1>,\vec F_<2>\). Поделив обе части равенства F1 d1 = F2 d2 на cos α, мы и придем к равенствам (7.2).
Точка C, таким образом, играет роль неподвижного шарнира, в котором следует закрепить рычаг A1A2, чтобы он оставался в равновесии под действием внешних сил \(\vec F_<1>,\vec F_<2>\). В качестве реакции шарнира надо рассматривать уравновешивающую \(\vec R’\).
Система из двух сонаправленных сил \(\vec F_<1>,\vec F_<2>\) имеет равнодействующую \(\vec R\), сонаправленную с ними. Ее модуль равен сумме исходных сил: R = F1 + F2, а положение ее линии действия между линиями действия исходных сил может быть определено по правилу рычага.
Найдем координаты точки C. Пусть A1 и A2 имеют радиус-векторы \(\vec r_<1>=\
| $$\vec r_ | (7.3) |
или, в координатной форме,
Замечание. Напомним, что точка C делит отрезок A1A2 в отношении λ, если она принадлежит прямой (не обязательно отрезку) A1A2 и \(\overrightarrow
С другой стороны, из уравнения (7.2) следует, что точка C делит отрезок A1A2 в отношении λ = F2/F1, считая от вершины A1. Подставляя это отношение в (7.3) и упрощая, получим окончательно:
| $$\vec r_ | (7.4) |
В частности, при F1 = F2 из (7.4) следует, что \(\vec r_
7.2. Сложение двух противоположно направленных сил
Рассуждая таким же образом, как и в предыдущем пункте, попробуем найти равнодействующую двух противоположно направленных сил \(\vec F_<1>\) и \(\vec F_<2>\). Без ограничения общности будем предполагать, что F1 ≤ F2. Все дополнительные построения и обозначения аналогичны тем, что введены на рис. 7.2.
Линии действия сил \(\vec Q_<1>,\vec Q_<2>\) по-прежнему пересекаются в точке B, что дает возможность отложить силы \(\vec F_<1>,\vec F_<2>\) от этой точки и найти их равнодействующую \(\vec R=\vec F_<1>+\vec F_<2>\) (рис. 7.4).
Рис. 7.4. Сложение двух противоположно направленных сил
За счет того, что \(\vec F_<1>\) и \(\vec F_<2>\) направлены противоположно, теперь модуль равнодействующей равен разности модулей исходных сил: R = F2 – F1. Вектор \(\vec R\) сонаправлен с \(\vec F_<2>\) (этот вектор имеет большую абсолютную величину).
При определении положения точки C можно по-прежнему использовать соотношение (7.1), но теперь эта точка находится вне отрезка A1A2 ближе к A2 (в этом конце отрезка приложена большая по модулю сила). Таким образом, теперь C делит отрезок A1A2 в отрицательном отношении λ = –F2/F1, считая от вершины A1. Подставив это значение в (7.3), найдем радиус-вектор точки приложения равнодействующей:
| $$\vec r_ | (7.5) |
Можно считать, что вместо (7.5) по-прежнему справедлива формула (7.4), если одну из величин F1 или F2 считать отрицательной, принимая во внимание противоположную направленность сил \(\vec F_<1>,\vec F_<2>\). При этом безразлично, какой именно величине, F1 или F1, приписать знак «–». В этом случае F1 и F1 будут уже не просто модулями \(\vec F_<1>,\vec F_<2>\), а проекциями сил на ось, сонаправленную с одним из векторов.
Итак, аналогично случаю двух сонаправленных сил, можно утверждать:
Система из двух не равных по величине противоположно направленных сил \(\vec F_<1>,\vec F_<2>\) имеет равнодействующую \(\vec R\), сонаправленную большей по модулю силой. Модуль равнодействующей равен модулю разности исходных сил: R = |F1 – F2|. Положение ее линии действия можно определить по правилу рычага, но она находится вне области, заключенной между линиями действия \(\vec F_<1>\) и \(\vec F_<2>\).
Оговорка о неравенстве сил по величине сделана не случайно, ее смысл поясняется ниже.
Выясним, что происходит с равнодействующей \(\vec R\) при различных соотношениях между F1 и F2. Если они равны по величине и знаку, то точка C, в которой приложена \(\vec R\), располагается в середине исходного отрезка A1A2, причем по модулю она будет в два раза больше, чем F1 или F2 (рис. 7.5 а).
Рис. 7.5. Равнодействующая при различных соотношениях между F1 и F2
Станем теперь уменьшать F1. Это приведет к тому, что будет уменьшаться и R, а точка C станет смещаться по направлению к A2 (рис. 7.5 б). При F1 = 0 мы получим, что R = F2, а из (7.4) следует, что в этом случае точки C и A2 совпадут. Впрочем, этот результат очевиден и без использования формул: фактически, при F1 = 0 на тело действует лишь сила F2. Если теперь поменять знак у F1 и тем самым «развернуть» \(\vec F_<1>\) в сторону, противоположную \(\vec F_<2>\), то C покинет отрезок A1A2 (рис. 7.5 в), а равнодействующая R окажется меньше, чем F2. При увеличении абсолютной величины F1 (с сохранением отрицательного знака) R продолжит уменьшаться, а C станет все больше и больше удаляться от A2.
Возникает вопрос: что произойдет при |F1| = |F2|, т.е. в случае, когда силы \(\vec F_<1>\) и \(\vec F_<2>\) образуют пару?
С одной стороны, величина равнодействующей (если таковая существует) станет равной нулю. С другой стороны, подставив F1 = –F2 в формулу (7.4) или F1 = F2 в (7.5), мы окажемся перед необходимостью делить на нуль. Следовательно, невозможно определить местоположение точки C – она «улетает» на бесконечность. Отсюда вытекает, что
Ранее этот факт уже упоминался без доказательства.
7.3. Сложение трех и более параллельных сил
Пользуясь результатами предыдущих пунктов, попытаемся найти равнодействующую нескольких (более двух) параллельных сил \(\vec F_<1>,\vec F_<2>,\ldots,\vec F_
Рис. 7.6. Система нескольких параллельных сил
Будем складывать силы попарно, аналогично тому, как ранее вычислялась равнодействующая сходящейся системы. В случае, когда сил всего три, рассуждения таковы. Сложив \(\vec F_<1>\) и \(\vec F_<2>\), найдем их равнодействующую \(\vec R_<1,2>\). Ее проекция на ось l равна сумме проекций \(\vec F_<1>\) и \(\vec F_<2>\), т.е. F1 + F2. Радиус-вектор \(\vec r_<1,2>\) точки приложения \(\vec R_<1,2>\) можно найти по формуле (7.4) с учетом знаков F1 и F2:
Итак, исходная система эквивалентна двум параллельным силам: \(\vec R_<1,2>\) и \(\vec F_<3>\), приложенным в точках с радиус-векторами \(\vec r_<1,2>\) и \(\vec r_<3>\), соответственно. Складывая их и упрощая выражения, найдем равнодействующую трех сил \(\vec R\), проекция которой на ось l составляет R = R1,2 + F3 = F1 + F2 + F3, а радиус-вектор точки приложения C равен
Аналогично, для произвольного количества n сил получим
\begin | (7.6) | |
В координатной форме второе равенство можно переписать так:
| $$x_ | (7.7) |
Конечно, знаменатель дроби в формулах для определения \(\vec r_
Пример. Параллельные силы \(\vec F_<1>,\vec F_<2>\) и \(\vec F_<3>\) имеют проекции 5 Н, –4 Н и 7 Н на направление вектора \(\vec F_<1>\) и приложены в точках A1(–1; 13; 6), A2(6; –3; 5) и A3(3; –3; 2), соответственно; все координаты даны в см. Найти равнодействующую этих сил и точку ее приложения.
Согласно первому из равенств (7.6), R = 5 – 4 + 7 = 8 Н. Тем самым, заданная система сил, действительно, имеет равнодействующую: R ≠ 0.
Вычислим координаты точки приложения найденной равнодействующей, используя (7.7):
xC = (–1·5 + 6·(–4) + 3·7)/8 = –1 см, yC = (13·5 – 3·(–4) – 3·7)/8 = 7 см, zC = (6·5 + 5·(–4) + 2·7)/8 = 3 см.
Соотношения (7.6) и (7.7) справедливы, если сумма проекций всех параллельных сил на одну и ту же ось l отлична от нуля. В противном случае система приводится не к равнодействующей, а к паре, аналогично п. 7.2.
Как следует из второй аксиомы статики, равнодействующая системы параллельных сил – скользящий вектор. Поэтому ее необязательно прикладывать в точке C, определяемой из формул (7.6). Достаточно выбрать любую точку на прямой, проходящей через C и имеющей \(\vec R\) в качестве направляющего вектора. Поэтому, используя указанное выше соотношение, мы накладываем на точку приложения равнодействующей дополнительное ограничение.
Зато появляется другая «свобода маневра». Ось l проводится не произвольно, а «привязывается» к самим параллельным силам. Соответственно, величины F1, F2. Fn описывают лишь ориентацию этих сил относительно друг друга. Если все векторы \(\vec F_<1>,\vec F_<2>,\ldots,\vec F_
Рис. 7.7. Поворот системы параллельных сил
Если система параллельных сил имеет равнодействующую, то ее величина и точка приложения не меняются при одновременном повороте всех сил на один и тот же угол и не зависят от ориентации сил относительно неподвижной системы координат.
Такая точка C, что при любом одновременном повороте системы параллельных сил линия действия ее равнодействующей проходит через C, называется центром параллельных сил. Из вышесказанного следует, что координаты этого центра могут быть вычислены по формуле (7.6), если, конечно, существует сама равнодействующая.
В частности, если силы \(\vec F_<1>,\vec F_<2>,\ldots,\vec F_
7.4. Распределенная нагрузка
Как уже было сказано в п. 1.1, силу (нагрузку) называют распределенной, если она приложена ко всем точкам некоторой линии, поверхности или объема. При проектировании различных механизмов, зданий и сооружений учет распределенных сил играет очень важную и даже решающую роль.
Пример 1. Одной из деталей двигателя внутреннего сгорания является поршень, размещаемый внутри цилиндра (рис. 7.8). При сгорании рабочая смесь воздуха и распыленного топлива в цилиндре расширяется и давит на поршень, толкая его. Это усилие передается на коленчатый вал, а от него – на оси колес автомобиля, что и заставляет их вращаться. Сила давления сгорающей смеси на поршень распределяется по площади его головки.
Рис. 7.8. Поршень с шатуном
Пример 2. Выпадающий снег может создавать значительное давление на крышу здания (рис. 7.9 а). Если эту снеговую нагрузку не учитывать, крыша может не выдержать и обрушиться (рис. 7.9 б).
Рис. 7.9. Снеговая нагрузка на крышу здания
Основная характеристика распределенной нагрузки – ее интенсивность (плотность, удельная нагрузка): сила, приходящаяся на единицу длины, площади или объема. Первые две величины называют также погонной нагрузкой и давлением, соответственно. В системе СИ интенсивность нагрузки измеряют в Н/м, Н/м 2 (паскалях – Па) и Н/м 3 в зависимости от того, распределена сила по длине, площади или объему.
Так, если давление p на участке поверхности площади S постоянно, то для вычисления суммарной силы F, действующей на этот участок, нужно умножить его площадь на давление: F = pS. После этого останется учесть направление приложенной силы (рис. 7.10).
Чтобы найти силу, действующую на всю поверхность (объем, длину), можно было бы умножить интенсивность нагрузки на общую площадь поверхности. Однако трудность заключается в том, что интенсивность распределенной нагрузки может быть не постоянной,а изменяться от точки к точке как по величине, так и по направлению.
Пример 1. При ходьбе босиком по песку пятка и пальцы оставляют более четкий след, чем остальная часть ступни (рис. 7.11). Это значит, что интенсивность нагрузки (в роли которой выступает вес человека), приходящейся на пальцы и пятку, выше.
Рис. 7.11. След на песке показывает, что вес человека распределен по его ступням неравномерно
Пример 2. Значительное влияние на устойчивость зданий и сооружений (особенно тех, что имеют большие размеры), оказывает ветровая нагрузка. Давление, создаваемое подвижными воздушными массами, изменяется от точки к точке и зависит от многих факторов: температуры, влажности и т.д. Ветровая нагрузка на сооружения может расчитываться с помощью ЭВМ. Кроме того, для моделирования такой нагрузки макеты сооружений могут обдуваться в аэродинамической трубе, подобно летательным аппаратам.
Часто можно предположить, что силы, приложенные во всех точках изучаемого объема (поверхности, линии) параллельны друг другу. Тогда можно попытаться найти их равнодействующую, пользуясь формулами (7.6).
Мы рассмотрим лишь простейшую ситуацию: силу, распределенную по прямолинейному отрезку. Будем предполагать, что силы, приложенные в разных точках, параллельны друг другу и перпендикулярны рассматриваемому отрезку. В этом случае наглядно представить интенсивность нагрузки можно с помощью специального графика – эпюры напряжений (рис. 7.12).
Рис. 7.12. Эпюра напряжений
Пусть нагрузка распределена по отрезку [a; b] оси Ox. Тогда величина погонной нагрузки p(x) в каждой конкретной точке зависит от координаты x этой точки. График функции p(x) и является искомой эпюрой.
Если выбрать на исходном отрезке [a; b] настолько мелкий участок Δx, что интенсивность нагрузки на его протяжении практически не успевает измениться, то суммарная сила ΔF, приложенная к этому участку, будет приближенно равна p(x)Δx (см. рис. 7.12). Значит, чтобы вычислить силу F, приложенную ко всему отрезку [a; b], надо разбить его на мелкие участки dx1, dx2. dxn, внутри каждого из них выбрать точку (x1, x2. xn, соответственно), приближенно вычислить силу, приложенную к этим участкам, а результаты сложить:
Действительно, силы, приложенные к разным участкам разбиения, параллельны друг другу (при введенных выше ограничениях), а значит, можно попытаться найти их равнодействующую по формуле (7.6). Чтобы определить координату точки приложения равнодействующей, используем равенство (7.7):
| $$x_ | (7.8 б) |
причем F вычисляется по формуле (7.8 а).
Конечно, результат вычислений в (7.8 а) и (7.8 б) будет тем точнее, чем мельче разбиение отрезка. В пределе, когда длины всех участков dx1, dx2. dxn стремятся к нулю (а их количество, соответственно, к бесконечности), сумма (7.8 а) переходит в определенный интеграл, а выражение для xC – в отношение двух интегралов:
Тем самым, суммарная нагрузка, приложенная к отрезку, представляет собой площадь криволинейной трапеции под графиком функции p(x).
Пример. Нагрузка распределена по отрезку [1; 4] с интенсивностью p(x) = –x 2 + 4x. Найти равнодействующую распределенных сил, приложенных к отрезку, и точку ее приложения.
Как и следовало ожидать для случая сонаправленных сил, точка приложения равнодействующей оказывается внутри отрезка: 1 ≤ 9/4 ≤ 4. Отметим, что p(1) = 3, p(4) = 0, так что правый конец отрезка не нагружен (рис. 7.13).
В наиболее простых случаях нагрузка распределяется по отрезку равномерно или линейно.
При равномерном распределении плотность p постоянна (рис. 7.14). В этом случае сосредоточенная равнодействующая равна произведению плотности на длину отрезка и прикладывается к его середине: F = p·(b–a), xC = (a + b)/2.
Рис. 7.14. Равномерно распределенная нагрузка
Пример. Нагрузку, создаваемую железнодородным составом на рельсы, можно считать равномерно распределенной: на каждый метр железнодорожного полотна, находящийся под составом, приходится примерно равный вес груза.
При линейном распределении погонная нагрузка возрастает от 0 на одном конце отрезка до некоторого значения pmax на другом конце; значения нагрузки в промежуточных точках пропорциональны расстоянию до ненагруженного конца. Для простоты рассмотрим отрезок [0; l] и предположим, что его левый конец свободен от нагрузки (рис. 7.15).
Рис. 7.15. Линейно распределенная нагрузка
Тогда получим p(0) = 0, p(l) = pmax, p(x) = pmax x/l. Подставив a = 0, b = l, а также найденное выражение для p(x) в (7.9), найдем F = lpmax/2, xC = 2l/3. Как и следовало ожидать, суммарная нагрузка равна площади прямоугольного треугольника с катетами pmax и l – именно такую фигуру ограничивает эпюра напряжений. Равнодействующая прикладывается на расстоянии, равном 2/3 длины отрезка, считая от ненагруженного конца.
Пример. Рассмотрим сваю, вертикально вбитую в дно водоема и испытывающую давление со стороны воды (согласно закону Паскаля, давление в жидкости не зависит от направления прилагаемого усилия, поэтому нельзя считать, что давление осуществляется только на горизонтальное дно водоема). Как известно из курса физики, указанное давление равно p = ρgz, где ρ – плотность жидкости, g – ускорение свободного падения, z – глубина, отсчитанная от свободной поверхности жидкости. Тем самым, интенсивность распределенной нагрузки линейно зависит от глубины z. Поэтому при замене распределенной нагрузки на сосредоточенную следует прикладывать равнодействующую на глубине, равной 2/3 глубины водоема (рис. 7.16).
Если силы, распределенные по объему (поверхности, линии) не параллельны, то можно по отдельности найти сосредоточенные равнодействующие \(\vec R_
Пример. Как уже говорилось, при жесткой заделке реактивная нагрузка распределяется по некоторой площади. При замене этой распределенной нагрузки на сосредоточенную возникает не только сила, но и реактивный момент.
Вопросы для самоконтроля
Задачи к лекции
Горизонтальная балка AE длины 7 м находится под действием сосредоточенной силы \(\vec F\), приложенной в точке D, находящейся на расстоянии 1 м от точки E, а также нагрузки, распределенной по отрезкам AB = 2 м и BC = 3 м. Отрезок AB нагружен равномерно с интенсивностью pmax = 100 кН/м, отрезок BC – линейно (рис. 7.17). Величина силы \(\vec F\) составляет 50 кН. Определить реакции жесткой заделки в точке A. Найти координату точки приложения сосредоточенной равнодействующей всех перечисленных сил (за исключением реакции заделки). Весом балки пренебречь.
Ответы. 1. A4(7; 1; 9). 2. XA = 0, YA = 300 кН, mA = 350 кН·м, x = 7/6 м. 3. Да.
Также рекомендуется решить задачи из §§3,4 [2]; РГР С1 [3].