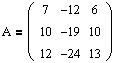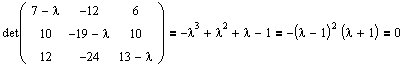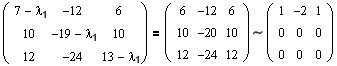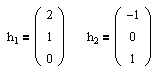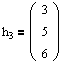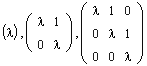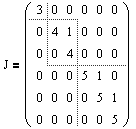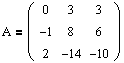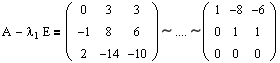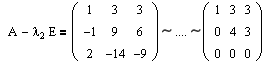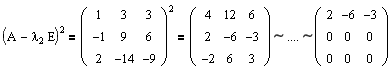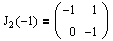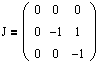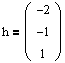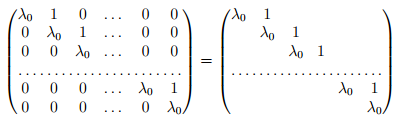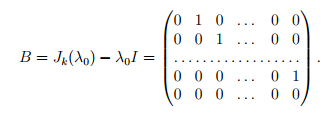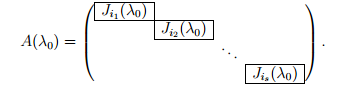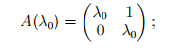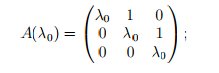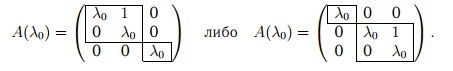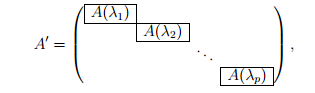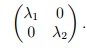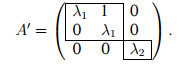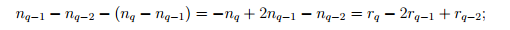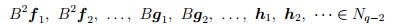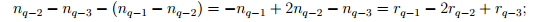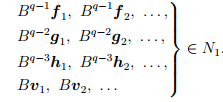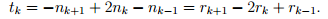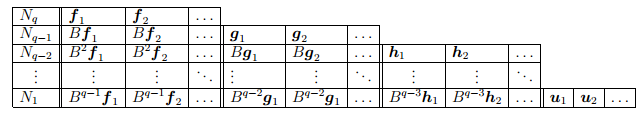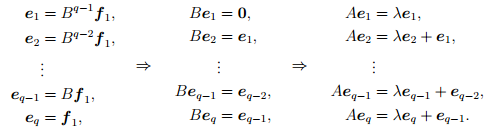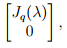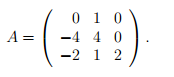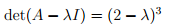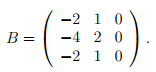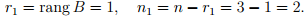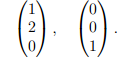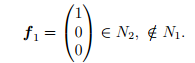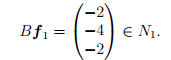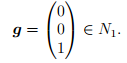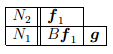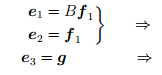как найти жорданову форму матрицы пример
Алгоритм нахождения векторов жорданова базиса
Собственные векторы и собственные значения
Пусть A – матрица некоторого линейного преобразования порядка n.
Определение. Многочлен n-ой степени
P(l)=det(A-lЕ) (1.1)
называется характеристическим многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы.
Определение. Ненулевой вектор x линейного пространства V, удовлетворяющий условию
А(х)=lх, (1.2)
называется собственным вектором преобразования A. Число l называется собственным значением.
Замечание. Если в пространстве V задан базис, то это условие можно переписать следующим образом:
Ах=lх, (1.3)
где A – матрица преобразования, x – координатный столбец.
Определение. Алгебраической кратностью собственного значения lj называется кратность корня lj характеристического многочлена.
Определение. Совокупность всех собственных значений называется спектром матрицы.
Алгоритм нахождения собственных значений и собственных векторов
1. Найти собственные значения матрицы:
· записать характеристическое уравнение:
det(A-lЕ)=0; (1.4)
· найти его корни l j, j=1. n и их кратности.
2. Найти собственные векторы матрицы:
· для каждого l j решить уравнение
· найденный вектор х и будет собственным вектором, отвечающим собственному значению l j.
Пример1
Найдем собственные значения и собственные векторы, если известна матрица преобразования:
Записываем характеристический многочлен (1.1) и решаем характеристическое уравнение (1.4):
Получаем два собственных значения: l1=1 кратности m1=2 и l2=-1 кратности m2=1.
Далее с помощью соотношения (1.5) находим собственные векторы. Сначала ищем ФСР для l1=1:
Очевидно, что rang=1, следовательно, число собственных векторов для l1=1 равно n-rang=2. Найдем их:
Аналогичным образом находим собственные векторы для l2=-1. В данном случае будет один вектор:
Понятие жордановой клетки и жордановой матрицы
Определение. Жордановой клеткой порядка m, отвечающей собственному значению l, называется матрица вида:
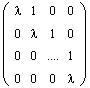
Иными словами, на главной диагонали такой матрицы располагается собственное значение l, диагональ, ближайшая к главной, сплошь занята единицами, а все остальные элементы матрицы равны нулю. Ниже даны примеры жордановых клеток соответственно первого, второго и третьего порядков:
Определение. Блочно-диагональная матрица, на диагонали которой стоят жордановы клетки, называется жордановой матрицей:
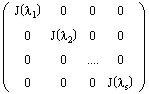
Пример
Ниже представлена жорданова матрица, состоящая из трех жордановых клеток:
— размера 1, отвечающая собственному значению l1=3;
— размера 2, отвечающая собственному значению l2=4;
— размера 3, отвечающая собственному значению l3=5.
Количество и размер жордановых клеток
Количество жордановых клеток размера k, отвечающих собственному значению lj, определяется следующим образом:
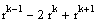
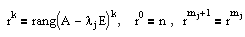
Пример
Пусть дана матрица преобразования:
Найдем количество и размер жордановых клеток, соответствующих каждому собственному значению этого преобразования.
Как искать собственные значения, было подробно рассказано в первом параграфе учебника. Поэтому опустим все расчеты, а сразу укажем собственные числа матрицы А: l1=0 кратности m1=1 и l2=-1 кратности m2=2.
Используя соотношения (3.1) и (3.2), найдем количество и размер жордановых клеток, соответствующих l1=0, m1=1.
Очевидно, что rang(A-l1E)=2 и, соответственно, r 1 =r 2 =rang(A-l1E) 1 =2, r 0 =n=3.
Ясно, что других клеток для этого собственного значения нет. Т.о., для l1=0, m1=1 мы имеем единственную жорданову клетку вида J1(0)=(0).
Далее аналогичным образом определяем клетки для второго собственного значения l2=-1 кратности m2=2.
Очевидно, что rang(A-l2E)=2 и, соответственно, r 1 =r 2 =rang(A-l2E) 1 =2.
Т.е. rang(A-l1E) 2 =1 и, соответственно, r 1 =r 2 =rang(A-l1E) 2 =1.
Теперь можно определить количество и размер жордановых клеток для второго собственного значения:
Таким образом, для l2=-1 мы получили одну клетку размера 2:
Соответственно, жорданова форма для исходной матрицы А будет иметь вид:
Жорданов базис
Пусть матрица А приведена к жордановой форме J. Рассмотрим систему HJ=AH, где
— матрица перехода от исходного базиса (e) к жорданову базису (h). Это система матричных n 2 уравнений с n 2 неизвестными.
Определение. Пусть e – собственный вектор преобразования А, т.е. имеет место равенство А(e) = le. Вектор e1, удовлетворяющий равенству
называется присоединенным вектором первого порядка;
вектор e2, удовлетворяющий равенству
— присоединенным вектором второго порядка;
вектор en, удовлетворяющий равенству
— присоединенным вектором n-ого порядка.
(А-lе) k ek=e. (4.5)
Алгоритм нахождения векторов жорданова базиса
Чтобы найти жорданов базис, необходимо проделать следующие действия для каждой жордановой клетки.
Рассмотрим жорданову клетку порядка k, отвечающую собственному значению l. Для нее ищутся вектора жорданова базиса:
Эта совокупность векторов ищется, используя следующую систему:
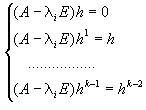
В результате применения этих операций ко всем жордановым клеткам, получим векторы, составляющие жорданов базис:
Векторам h соответствует жорданова клетка размера k, векторам f – размера p и т.д.
ex3
Пример
Вернемся к примеру, рассмотренному в прошлом разделе. Там нами были получены две жордановы клетки:
J1(0)=(0) и
Рассмотрим первую, J1(0).
С помощью соотношения (1.5) из первого параграфа найдем собственный вектор, отвечающий собственному значению l1=0:
Присоединенных векторов для данной жордановой клетки, очевидно, нет.
Теперь рассмотрим вторую жорданову клетку, J2(-1). Очевидно, что для нее надо найти один собственный вектор и один присоединенный.
Используя систему (4.6), получим эти векторы:
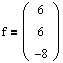
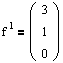
Мы получили все векторы, составляющие матрицу Н. Таким образом, матрица перехода к жорданову базису будет иметь следующий вид:
Жорданова нормальная форма матрицы оператора, жорданов базис.
Материал для изучения нормальной жордановой формы матрицы и жорданова базиза. Работа содержит теоретический материал, теоремы и примеры.
Просмотр содержимого документа
«Жорданова нормальная форма матрицы оператора, жорданов базис.»
Жорданова нормальная форма матрицы оператора, жорданов базис.
Определения и основные понятия
Введем два основных понятия.
1.1 Жорданова клетка
Жордановой клеткой порядка k, относящейся к числу λ0, называется матрица порядка k, 1≤k≤n, имеющая вид:
Также можем сказать, что на её главной диагонали стоит одно и то же число из поля P, а параллельные элементы, ближайшие к главной диагонали сверху, равны 1, все остальные элементы матрицы равны нулю.
Её характеристический многочлен (λ0 − λ) k имеет корень λ0 кратности k.
Таким образом, данная матрица имеет собственное значение λ0 алгебраической кратности k. Отвечающие ему собственные векторы — это ненулевые решения однородной системы линейных уравнений с матрицей
Так как rangB = k −1, так что размерность собственного подпространства равна 1, то существует лишь один линейно независимый собственный вектор. Таким образом, при k ≥ 2 не существует базиса, состоящего из собственных векторов этого оператора, то есть ни в одном базисе матрица оператора не может иметь диагонального вида. Матрица Jk(λ0) называется жордановой клеткой порядка k, соответствующей собственному значению λ0.
Жордановым блоком, отвечающим собственному значению λ0, называется блочно-диагональная матрица, каждый блок которой представляет собой жорданову клетку вида:
Все элементы матрицы вне жордановых клеток равны нулю. Порядок расположения жордановых клеток в матрице A(λ0) определен неоднозначно.
1.3 Примеры жордановых блоков
Рассмотрим простой случай, когда характеристический многочлен матрицы имеет вид f(λ) = (λ0 − λ) m и геометрическая кратность собственного значения λ0 равна s.
Пример 1. Пусть m = 2, s = 1. Тогда
имеем одну жорданову клетку порядка 2.
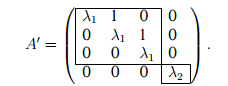
Пример 2. Пусть m = 3, s = 1. Тогда
имеем одну жорданову клетку порядка 3.
Пример 3. Пусть m = 3, s = 2. Имеем жорданов блок, состоящий из двух жордановых клеток порядков 1 и 2:
Теорема о жордановой форме матрицы оператора
Пусть линейный оператор A действует в линейном пространстве над полем комплексных чисел размерности n и его характеристический многочлен имеет вид
Тогда в этом пространстве существует базис, состоящий из собственных и присоединенных векторов оператора A, в котором матрица оператора имеет блочно-диагональную форму (она называется жордановой формой)
где A(λj ) — жорданов блок, соответствующий собственному значению λj. Указанный базис называется жордановым.
Сформулированная теорема верна и в случае, когда линейный оператор действует в линейном пространстве над произвольным числовым полем K, но все корни характеристического многочлена принадлежат полю K.
Рассмотрим примеры. Обозначаем через n размерность пространства, mj и sj — алгебраическую и геометрическую кратности собственного значения λj соответственно.
Пример 1. Пусть n = 2, λ1 ≠ λ2. Тогда матрица оператора может быть приведена к диагональному виду:
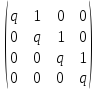
Базис векторного пространства, в котором матрица оператора имеет вид одной сплошной ячейки, должен обладать свойством («цикличность»), которое получим на основе правила «столбцы матрицы = образы базисных векторов».
Здесь q обозначает некое, известное нам число.
Это означает, что координаты вектора e1 в этом базисе равны (1,0,0,0).
Как нетрудно проверить, верно и обратное: если первый базисный вектор является по совместительству собственным вектором оператора с собственным числом q, то первый столбец матрицы оператора в таком базисе равен (q,0,0,0).
Теперь займемся вторым базисным вектором e2. Его координаты равны (0,1,0,0). Умножив на столбец (0,1,0,0) нашу матрицу, мы получим в качестве результата ее второй столбец (1,q,0,0). Это означает, что
Точно так же получаются равенства
В итоге мы приходим к выводу: если матрица оператора A в некотором базисе имеет вид Жордановой клетки (ячейки) с числом q на диагонали и с единичкам над ней, то векторы базиса превращаются друг в друга под воздействием оператора B=A-qE:
В этой цепочке стрелки (слева направо) показывают, что из каждого базисного вектора получается под воздействием оператора B.
4 Построение жорданова базиса и жордановой формы матрицы
Пусть λ — собственное значение оператора, m и s — алгебраическая и геометрическая кратности числа λ. Опишем построение линейно независимой совокупности из m собственных и присоединенных векторов, отвечающих данному λ. Этой совокупности векторов в жордановой матрице A′ будет соответствовать жорданов блок A(λ).
Теорема. Существует такое натуральное число q, что
т.е. все ядра с номером, большим, чем q, совпадают с ядром Nq. При этом
Построим часть жорданова базиса, соответствующую данному собственному значению λ, следующим образом.
1. Возводя матрицу B в последовательные натуральные степени, найдем показатель q, начиная с которого ранг степеней матрицы B перестает уменьшаться.
таким же будет количество жордановых клеток порядка q − 1.
таким же будет количество жордановых клеток порядка q − 2.
Процесс продолжаем аналогично. Наконец, рассмотрим ядро N1 и векторы
Итак, мы описали процесс построения жорданова базиса и выяснили, что количество жордановых клеток порядка k, входящих в состав жордановой формы матрицы оператора, может быть найдено по формуле
Построенную часть жорданова базиса, состоящую из m векторов, соответствующих данному λ (m — алгебраическая кратность этого собственного значения), запишем в таблицу («жорданова лестница»):
Все векторы таблицы линейно независимы, и их число равно m (алгебраической кратности собственного значения λ). Каждому столбцу этой таблицы соответствует одна жорданова клетка, порядок которой равен высоте столбца. Количество столбцов жордановой лестницы, т.е. полное количество жордановых клеток в блоке, соответствующем собственному значению λ, равно геометрической кратности s этого собственного значения.
Будем нумеровать векторы построенной части базиса по столбцам жордановой лестницы: внутри каждого столбца снизу вверх, а сами столбцы в произвольном порядке.
где Jq(λ) — жорданова клетка порядка q с числом λ на главной диагонали.
В следующих q столбцах матрицы A′, определенных векторами второго столбца жордановой лестницы, расположена жорданова клетка Jq(λ) так, что числа λ стоят на главной диагонали матрицы A′, а элементы вне клетки равны нулю. Подобным образом для данного λ получаем m столбцов матрицы A′. На этих m столбцах находится жорданов блок A(λ).
Для других собственных значений эта схема повторяется, в результате чего получим жорданову матрицу A′ и соответствующий жорданов базис.
4.1 Пример решения задач
Дана матрица A линейного оператора в некотором базисе. Требуется найти жорданов базис и жорданову форму матрицы оператора в этом жордановом базисе. Рассмотрим пример решения такой задачи методом построения жорданова базиса.
имеет корень λ = 2 кратности 3, т.е. m = 3. Матрица B = A − λI равна
Легко проверить, что
Собственные векторы находим, решив однородную систему линейных уравнений BX = O; фундаментальная совокупность решений состоит из двух векторов, например,
Количество этих векторов (т.е. геометрическая кратность собственного значения) равно двум, s = 2, так что для построения жорданова базиса требуется еще один присоединенный вектор.
Дополним базис ядра N1, т.е. набор векторов (2), до базиса ядра N2, например, вектором
Построим жорданову лестницу:
соответствует жорданова клетка порядка 2,
Жорданова нормальная форма матриц
Вот тут уже пошла Высшая Алгебра. Как студент Мех-Мата я могу сказать, что это чуть ли не самая важная теорема (о жордановой нормальной форме) в годовом курсе линейной алгебры. Сегодня для меня важно вспомнить алгоритм нахождения жордановой нормальной формы (далее ЖНФ) для матриц. Этот интерес не случаен, а связан он с тем, что скоро мне, как и всему четвёртому курсу Мех-Мата, предстоит пройти письменный государственный экзамен. Даже если у вас не такая весомая мотивация, то всё равно предлагаю остаться и посмотреть, что происходит, поверьте, алгебра — это интересно! Давайте начинать)
Всё объяснять сам я не буду по двум причинам. Лень, во-первых) Во-вторых, возможно у меня не хватит компетентности. Но взамен я предлагаю вам обращаться вместе со мной к другим уважаемым алгебраистам и перенимать их опыт и знания. А я, подобно барду, буду управлять сюжетом этой баллады.
Для начала нам нужно понять, что такое ЖНФ, из чего она состоит, и зачем она, вообще, нужна. Сходим на пару ВШЭ и узнаем.
Здесь нам Ирина Кузьмина рассказала теорему Фробениуса-Перрона, и мы должны понять, что не каждая квадратная матрица может быть записана в диагональном виде…
Т.е. когда некоторые из собственных значений спектра матриц могут совпадать. Напомню, что спектром называется множество всех собственных чисел матрицы.
Ирина ответила на главный вопрос — зачем нужна ЖНФ. Ответ: чтобы брать функции от матриц. Если мы хотим найти sin(A), cos(A), exp(A), A², A^(sqrt(2)) и др., то нам может помочь ЖНФ.
Ещё важно понять, что ЖНФ может состоять из нескольких жордановых клеток (в том числе и одной), где каждая из них будет отвечать за своё собственное число λ (греческая буква «лямбда»). Оно как раз будет располагаться по диагонали, а выше диагонали будут идти единички. Если ЖК (жорданова клетка) у нас будет размера 1х1, то тогда это будет просто λ. Все остальные элементы ЖК равны нулю. В общем виде выглядит ЖК вот так:
Для примера рассмотрим такую жорданову матрицу, которая состоит из трёх ЖК. Спектр матрицы будет содержать числа 2, 0, 3. Третья ЖК состоит только из λ = 3.
В общем виде, если мы найдём ЖНФ, то она будет выглядеть так:
Теперь пойдём по пути теории и ответим на вопрос, как так вышло, что ЖНФ существует. Для этого заглянем на мини-лекцию Алексея Савватеева, который нам расскажет как же строить жорданов базис, векторы в котором можно собрать, и получить матрицу перехода к ЖНФ.
Это непростая теория, так что приготовьтесь к таким терминам, как векторы, ядро линейного оператора, инвариантное подпространство… Всё это нужно, если вы хотите понять, как и что получилось, а также почему это, вообще, можно делать. Но если вы не хотите углубляться в теорию, то нужно найти какой-то простой способ нахождения ЖНФ. Ведь должны же быть другие способы нахождения этого важного математического объекта. Существуют ли другие способы. Ответ: да, существует множество способов. Более того, мы даже можем угадать ЖНФ, а потом доказать, что это именно она, но это уже высший пилотаж. Что же делать нам, простым смертным? Нужен понятный и относительно простой алгоритм.
Однако если вы на этом этапе не до конца поняли, что значит «найти жорданов базис», что такое ЖНФ, как это всё работает, и зачем мы делаем то, что делаем, то предлагаю вам ознакомиться с суперподробным видео Екатерины Пелипенко (рекомендую смотреть на скорости 1,5).
Кстати, Екатерина рассказывает про миноры (определители меньшей размерности, чем исходная матрица А), а также находит НОД (наибольший общий делитель) полиномов второй степени, полученных как миноры характеристической матрицы для А. Ещё попутно можно вспомнить, что такое ФСР (фундаментальная система решений). Для кого-то это может быть полезным.
PPS: Евгения в своём видео также находит трансформирующую матрицу (тоже самое, что и матрица перехода). Она обозначила её за U, но обычно (как было на моих лекциях) она обозначается как T (transition matrix). Принципиально это ничего не меняет.
3PS: Если вы до конца посмотрели видео Евгении и захотели сделать проверку, то выкладываю её, дабы не тратить ваше время на перемножение матриц.
При просмотре видео вы могли заметить, что Евгения решает систему из 9 линейных уравнений. Это может показаться сложноватым, но не пугайтесь. Все действия просты, нужно лишь сконцентрироваться! Поэтому алгебра и читается на первом курсе вуза, а не в школе.
Я хотел бы рассказать про ещё один способ нахождения ЖНФ через ниль-слои. Хорошего и подробного видео, к сожалению, мне найти не удалось. В такой ситуации я могу сделать ссылку на очень хорошую методичку В. А. Чуркина, кандидата физико-математических наук. Здесь подробно изложено нахождение ЖНФ данным методом. Кроме того, данное пособие стоит прочесть тем, кто хочет глубже погрузиться в курс линейной алгебры.
Ладно, для закрепления всего этого материала предлагаю посмотреть ещё несколько примеров на популярном сайте Math Help Planet. Надеюсь, что всё это было достаточно подробно.
Я старался сделать статью математически формальной, насколько это было возможно, но и в то же время доступной для широкого круга читателей нашей группы ВК. Надеюсь, вы приятно и продуктивно потратили время. Сегодня мы затронули тему из линейной алгебры, вы поняли как и зачем искать ЖНФ, а я имел удовольствие написать данную статью. Если остались вопросы, вы можете задавать их в комментариях.
Желаю вам успехов в дальнейшем изучении математики, всего вам наилучшего!
5PS: Статья была отредактирована, добавлены ссылки к ключевым определениям, которые лучше позволяют понять материал.