как называется форма земли ограниченная основной уровенной поверхностью
Тема: Общие сведения по геодезии. Предмет геодезии
1. Что такое геодезия
_______ Геодезия – это наука об измерениях на земной поверхности, выполняемых для изучения общей фигуры Земли, для составления планов и карт, для решения инженерных задач при изысканиях, проектировании, строительстве и эксплуатации инженерных сооружений.
_______ В процессе своего развития геодезия разделилась на ряд самостоятельных научных дисциплин: высшую геодезию, топографию, инженерную геодезию, аэрофотогеодезию, картографию и космическую геодезию.
_______ Высшая геодезия занимается определением фигуры и размеров всей Земли и значительных ее частей.
_______ Топография занимается измерением и изображением на планах и картах земной поверхности.
_______ Инженерная геодезия занимается вопросами геодезических работ при изысканиях, проектировании, строительстве и эксплуатации инженерных сооружений, при монтаже оборудования, при наблюдениях за вертикальными и горизонтальными смещениями инженерных сооружений и технологического оборудования.
_______ Аэрофотогеодезия занимается изучением методов и средств создания топографических карт и планов по материалам фотографирования Земли.
_______ Картография занимается изучением методов составления, издания и использования карт.
_______ Космическая геодезия занимается обработкой измерений, полученных при помощи искусственных спутников Земли, орбитальных станций и межпланетных кораблей.
_______ Геодезия имеет тесную связь с другими научными дисциплинами: математикой, астрономией, физикой, механикой, автоматикой, электроникой, географией, фотографией и черчением.
2. Предмет геодезии. Понятие о форме и размерах Земли
_______ Геоид – это геометрическое тело, ограниченное уровенной поверхностью.
 |
_______ Уровенная поверхность – поверхность, совпадающая с поверхностью воды в морях и океанах, которые находятся в спокойном состоянии, продолженная под материками.
 |
3. Способы изображения земной поверхности. Метод проекций в геодезии
_______ При изучении действительной поверхности Земли точки местности проецируют отвесными линиями на поверхность земного эллипсоида. Так как уровенная поверхность радиусом до 20 км может быть заменена плоскостью, при относительно небольших площадях, точки местности проецируют на горизонтальную плоскость. Положение полученных проекций точек может быть определено координатами.
_______ В результате перенесения точек на плоскость длины линий заменяют их горизонтальными проекциями, называемыми горизонтальными проложениями ; пространственные углы заменяются плоскими, и вся фигура заменяется проекцией на горизонтальную плоскость (рис. 2).
 |
4. Системы координат, принятые в геодезии
_______ В геодезии применяются следующие системы координат:
• Географическая система координат,
• Зональная система плоских прямоугольных координат Гаусса–Крюгера,
• Полярная система координат.
4.1. Географические координаты
 |
_______ С помощью географических координат, то есть широт ( φ ) и долгот ( λ ), определяют положение точки относительно экватора и начального меридиана.
_______ Широтой (φ) точки называется угол, составленный отвесной линией в данной точке и плоскостью экватора.
_______ Долготой (λ) точки называется двугранный угол между плоскостью меридиана данной точки и плоскостью начального меридиана.
4.2. Зональная система плоских прямоугольных координат Гаусса–Крюгера
_______ Изображение осевого меридиана принимается за ось абсцисс (x), изображение экватора – за ось ординат (y). За начало координат принимают точку пересечения осевого меридиана с экватором.
Зональная система плоских прямоугольных координат Гаусса–Крюгера
 |
 |
_______ Зная географические координаты точки земной поверхности, можно вычислить зональные прямоугольные координаты, и, наоборот.
4.3. Полярная система координат
_______ В полярной системе координат используются полярные углы и расстояния. Подробнее эта система будет рассмотрена в последующих лекциях.
5. Системы высот, принятые в геодезии
_______ Абсолютная высота – длина перпендикуляра, опущенного из точки на уровенную поверхность, принятую за начало отсчета (поверхность эллипсоида).
 |
 |
 |
6. Ориентирование линий
_______ Ориентировать линию – значит определить ее направление относительно исходного меридиана.
_______ Азимуты изменяются от 0º до 360º.
_______ Азимут одной и той же линии в разных ее точках различен. Меридианы разных точек не параллельны между собой, так как они сходятся в точках полюсов. Отсюда азимут линии в разных ее точках имеет разное значение. Угол между направлениями двух меридианов называется сближением меридианов и обозначается γ.
 |
_______ Для перехода от магнитного азимута к истинному надо знать величину и название склонения магнитной стрелки δ. Склонение магнитной стрелки указывается в зарамочном оформлении листа топографической карты.
_______ Дирекционным углом называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана или линии ему параллельной по часовой стрелке до направления данной линии. Обозначается буквой α.
_______ Дирекционные углы бывают прямыми и обратными (рис.10).
 |
_______ Обратный дирекционный угол вычисляется по формуле:
 |
_______ Румбом называется острый угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии (r).
Румб всегда сопровождается названием четверти, в которой расположена линия (рис. 11).
 |
7. Съемки
_______ Для составления планов и карт необходимо на местности производить геодезические измерения. Комплекс таких измерений называется съемкой.
Форма Земли, или что такое геоид
Всем привет. Из дискуссий о форме Земли я часто замечаю, что люди знают слово геоид, но зачастую не представляют, что именно это слово означает. Хочу тезисно осветить тему.
В последующие века геодезия (наука о фигуре Земли) продолжала развиваться, а с появлением космических аппаратов в 20 веке появилась и спутниковая геодезия, с помощью которой удалось дополнительно уточнить параметры фигуры Земли.
В качестве системы описания параметров Земли используется WGS 84 или её российский аналог ПЗ-90. В качестве отсчётного тела используется общеземной эллипсоид вращения с большой полуосью (то есть средним экваториальным радиусом) 6378 км и сжатием эллипсоида 1/298. [3]
Например сверху Северный полюс, снизу Южный, вращаем этот эллипс вокруг оси, проходящей через полюса, и получаем общеземной эллипсоид вращения. Внимание, вопрос: видите ли вы отличие этого эллипса от окружности? Вряд ли. Поэтому если вы упоминаете сплюснутость Земли сами или слышите о сплюснутости от другого человека, вспоминайте эту картинку.
В некоторых сетевых дискуссиях люди меня уверяли, что если фигура хоть сколько-то отличается от шара, то это уже не шар. Вот такая, понимаете ли, принципиальность. Мои попытки рассказать этим людям, что идеальных геометрических фигур в физической реальности не существует, были не очень успешны. И когда я демонстрировал вышеприведённую картинку и спрашивал, чем же она так отличается от окружности, мне либо говорили, что я рисую вообще что-то не то, либо разводили руками.
Из вышесказанного вы уже понимаете, что вторым приближением к форме Земли является общеземной эллипсоид вращения (с вышеуказанными величинами большой полуоси и сжатия). Если представить себе Землю без суши, с ровным дном и без неоднородных вкраплений (плотные породы и тому подобное), то форма Земли (а именно поверхность мирового океана) с хорошей точностью совпадала бы с эллипсоидом вращения.
К слову, эллипсоид вращения и образовался как раз из-за суточного вращения нашей планеты, и когда возникает вопрос «почему нет горба воды в районе экватора из-за вращения», я отвечаю, что «горб» как раз есть, но он размазан между экватором и полюсом. Сумма гравитационной и центробежной сил как раз и дают направление силы тяжести (локальной вертикали), которая практически перпендикулярна к нашему эллипсоиду.
Практически перпендикулярна, однако в следующем, третьем приближении, есть отклонения направления силы тяжести (называется уклонением отвеса), связанные с неоднородностями: неровная поверхность суши и дна водоёмов, а также неравномерное распределение плотностей во внутренней структуре Земли. Это приводит к тому, что реальная поверхность мирового океана отличается от эллипсоида на величины до 100 метров. Такая уровенная поверхность невозмущённой поверхности мирового океана, причём продолженная под континентами, и называется геоидом. [4]
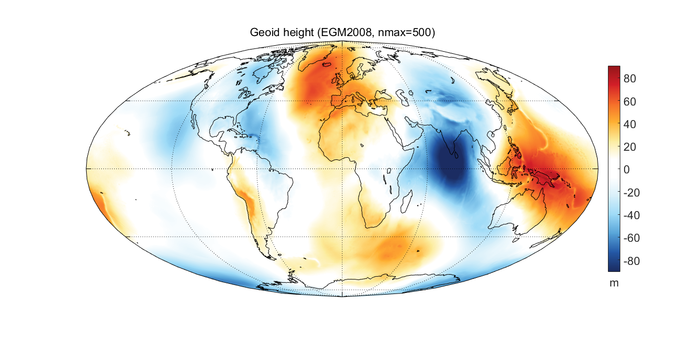
Так выглядит карта высот геоида относительно эллипсоида:
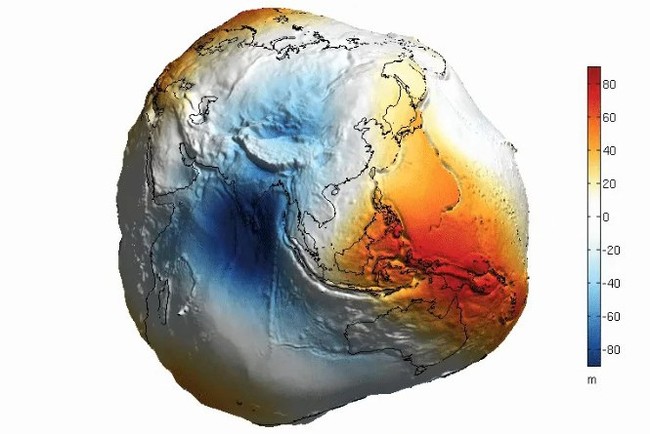
Понятно, что если на глаз трудно отличить даже 20-километровую сплюснутость Земли (эллипсоид в сравнении с шаром), то отличия геоида от эллипсоида в десятки метров в масштабе были бы тем более незаметны. Поэтому для целей визуализации отличий геоида от эллипсоида (не от шара, подчёркиваю) была сделана картинка, в которой эти отличия были утрированы на несколько порядков. А затем эту картинку кто-то вбросил со словами «так выглядит Земля без воды!» И почему-то этот вброс в своё время приобрёл вирусный характер, и до сих пор многие так и продолжают считать, что это форма Земли без воды:
Ну и завершим мы такой, например, вполне подходящей картинкой, на которой не в масштабе, а условно приведены разные поверхности всех трёх приближений к форме Земли (сфера, эллипсоид вращения, геоид):
[1] Эти измерения проводили с помощью триангуляционной разметки на Земле и последующих астрономических измерений высоты кульминации выбранной звезды.
[3] Приведённые значения округлены, более точные значения составляют 6378136 метров и 1/298.258.
Основы геодезии
О геодезии и разный полезный материал для геодезистов.
Понятие о фигуре Земли
Фигура Земли как планеты издавна интересовала ученых; для геодезистов же установление ее фигуры и размеров является одной из основных задач.
На вопрос: “Какую форму имеет Земля?” большинство людей отвечает: “Земля имеет форму шара!”. Действительно, если не считать гор и океанических впадин, то Землю в первом приближении можно считать шаром. Она вращается вокруг оси и согласно законам физики должна быть сплюснута у полюсов. Во втором приближении Землю принимают за эллипсоид вращения; в некоторых исследованиях ее считают трехосным эллипсоидом.
На поверхности Земли встречаются равнины, котловины, возвышенности и горы разной высоты; если же принять во внимание рельеф дна озер, морей и океанов, то можно сказать, что форма физической поверхности Земли очень сложная. Для ее изучения можно применить широко известный способ моделирования, с которым школьники знакомятся на уроках информатики.
При разработке модели какого-либо объекта или явления учитывают только его главные характеристики, имеющие значение для успешного решения данной конкретной задачи; все другие характеристики, как несущественные для данной задачи, во внимание не принимаются.
В модели шарообразной Земли поверхность Земли имеет сферическую форму; здесь важен лишь радиус сферы, а все остальное – морские впадины, горы, равнины, – несущественно. В этой модели используется геометрия сферы, теория которой сравнительно проста и очень хорошо разработана.
Модель эллипсоида вращения имеет две характеристики: размеры большой и малой полуосей. В этой модели используется геометрия эллипсоида вращения, которая намного сложнее геометрии сферы, хотя разработана также достаточно подробно.
Если участок поверхности Земли небольшой, то иногда оказывается возможным применить для этого участка модель плоской поверхности; в этой модели применяется геометрия плоскости, которая по сложности (а точнее, по простоте) несравнима с геометрией сферы, а тем более с геометрией эллипсоида.
В одном из учебников по высшей геодезии написано: “Понятие фигуры Земли неоднозначно и имеет различную трактовку в зависимости от использования получаемых данных”. При решении геодезических задач можно иногда считать поверхность участка Земли либо частью плоскости, либо частью сферы, либо частью поверхности эллипсоида вращения и т.д.
Какое направление вполне однозначно и очень просто можно определить в любой точке Земли без специальных приборов? Конечно же, направление силы тяжести; стоит подвесить на нить груз, и натянутая нить зафиксирует это направление. Именно это направление является в геодезии основным, так как оно существует объективно и легко и просто обнаруживается. Направления силы тяжести в разных точках Земли не параллельны, они радиальны, то-есть почти совпадают с направлениями радиусов Земли.
Поверхность, всюду перпендикулярная направлениям силы тяжести, называется уровенной поверхностью. Уровенные поверхности можно проводить на разных высотах; все они являются замкнутыми и почти параллельны одна другой.
Уровенная поверхность, совпадающая с невозмущенной поверхностью мирового океана и мысленно продолженная под материки, называется основной уровенной поверхностью или поверхностью геоида.
Если бы Земля была идеальным шаром и состояла из концентрических слоев различной плотности, имеющих постоянную плотность внутри каждого слоя, то все уровенные поверхности имели бы строго сферическую форму, а направления силы тяжести совпадали бы с радиусами сфер. В реальной Земле направления силы тяжести зависят от распределения масс различной плотности внутри Земли, поэтому поверхность геоида имеет сложную форму, не поддающуюся точному математическому описанию, и не может быть определена только из наземных измерений.
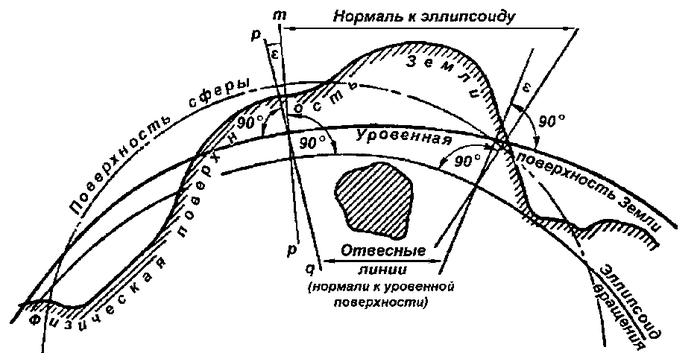
В настоящее время при изучении физической поверхности Земли роль вспомогательной поверхности выполняет поверхность квазигеоида, которая может быть точно определена относительно поверхно сти эллипсоида по результатам астрономических, геодезических и гравиметрических измерений. На территории морей и океанов поверхность квазигеоида совпадает с поверхностью геоида, а на суше она отклоняется от него в пределах двух метров /24/ (рис.1.1).
За действительную поверхность Земли принимают на суше ее физическую поверхность, на территории морей и океанов – их невозмущенную поверхность.
Что значит изучить действительную поверхность Земли? Это значит определить положение любой ее точки в принятой системе координат. В геодезии системы координат задают на поверхности эллипсоида вращения, потому что из простых математических поверхностей она ближе всего подходит к поверхности Земли; поверхность этого эллипсоида называется еще поверхностью относимости. Элли псоид вращения принятых размеров, определенным образом ориентированный в теле Земли, на поверхность которого относятся геодезические сети при их вычислении, называется референц-эллипсоидом.
Для территории нашей страны постановлением Совета Министров СССР N 760 от 7 апреля 1946 года принят эллипсоид Красовского:
большая полуось a = 6 378 245 м, малая полуось b = 6 356 863 м, полярное сжатие:
Применяемые в разных странах референц-эллипсоиды могут иметь неодинаковые размеры; существует и общеземной эллипсоид, размеры которого утверждают Международные геодезические организации. Так, в системе WGS-84 (World Geodetic System) эти размеры суть большая полуось a = 6 378 137.0 м, полярное сжатие:
Малая полуось при необходимости вычисляется через a и α.
Для многих задач геодезии поверхностью относимости может служить сфера, которая в математическом отношении еще проще, чем поверхность эллипсоида вращения, а для некоторых задач небольшой участок сферы или эллипсоида можно считать плоским.
9. Какую форму имеет Земля?
Из книги «Восприятие и познание мира» З.С. Беловой:
(стр. 35) «Безусловно, целостная картина мира в сознании человека – это продукт эволюции, она меняется в разных культурах, в разные исторические эпохи. В этой связи особый познавательный интерес вызывает история становления представления людей о форме Земли.
Земля представлена была как плоский круг, обращённый лицом к зрителю. …Пытаясь убеждать и других, астрономы усовершенствовали эту модель. Теперь Земля представляла как выкуплый диск, лежащий на спине слона, который стоит на спине черепахи, а последняя плавает, в свою очередь, в безбрежном океане».
Думаю, данное видение было взято из мифологии и не правильно истолковано. Безбрежный океан – это космическое пространство, то есть не пустота. Выпуклый диск – это сфера. Слон – это основа, а именно ось вращения Земли. Черепаха имеет выпуклый панцирь, то есть положение слона (оси Земли) на ней устойчивое только в определённой точке. Так я мыслю скрытый смысл мифа. Конечно, он основан на тех знаниях, что я имею.
«На протяжении тысячелетий считалось очевидной истинной, что Земля плоская. Думать иначе казалось абсурдом. Но древнегреческий мыслитель Пифагор пришёл к выводу, что Земля имеет форму шара. Вероятно, этот вывод имел под собой эмпирическую базу, но аргументация, приведённая самим Пифагором, вытекала из идеи совершенства и гармонии мира, столь важной для мировоззрения. Воплощением гармонии формы является сфера, потому, по убеждению, Пифагора, Земля должна иметь сферическую форму.
Дальнейшее развитие концепции шарообразности Земли было осуществлено в IV веке до н.э. крупным учёным Древней Греции Аристотелем. Он указал на то, что при приближении к высоким объектам первоначально появляются из-за горизонта их верхние, а затем уже нижние части, а также на то, что при передвижении на север или на юг высота Полярной звезды над горизонтом изменяется. Эти явления, конечно же, свидетельствовали о кривизне земной поверхности и вполне согласовывались с предположением, что Земля – это шар, но ещё не доказывали его.
По мере углубления познания гипотеза о форме Земли уточняется, конкретизируется по схеме, близкой к логике восхождения от абстрактного к конкретному. История развития этой гипотезы показала, что первоначальная умозрительная идея является своего рода абстракцией, но такой, которая выполняет роль модельного представления реальности».
Получается, что окружающий мир, тот, который мы видим и ощущаем, существует только в нашем сознании и изменяется по мере его развития. Так ли это? А как же прошлое и будущее? Для нас существует только настоящее. Оно и влияет на наши представления о прошлом и будущем.
«На следующем этапе развития гипотезы Земля была представлена как эллипсоид вращения, то есть как тело, которое образуется от вращения эллипса вокруг его малой оси. Известно, что тело тем больше сплющено, чем быстрее совершается его вращение вокруг собственной оси. Предполагалось, что тело, переставшее вращаться снова примет форму шара».
Значит ли это, что изменчива сама форма Земли или же изменчивы наши представления об этой форме?
«В связи с этим выяснилось, что форма Земли явно отклоняется от правильного шара: во-первых, благодаря вращению вокруг своей оси приобрела форму эллипсоида, во-вторых, эллипсоид утончается в форме геоида.
Фигура Земли, построенная только по зональным характеристикам, имеет грушевидную форму, вытянутую к северу и сплюснутую с юга. Таким образом, Земля обладает ещё одной чётко выраженной формой – грушевидностью».
Неудивительно, так как один полюс Земли повёрнут к Солнцу.
«Шар, эллипсоид, геоид, грушевидность – суть различных гипотез. Они или исключают, или дополняют друг друга. Ответить на вопрос, какова же форма Земли, могли учёные не столько простыми умозаключениями, сколько измерениями, наблюдениями, экспериментом.
Карта Земли при некотором преувеличении должна выглядеть как эллипс. Считать Землю эллипсом удобно, ибо это – простая геометрическая поверхность и её легко отобразить на картах. Эллипсоид описывается простыми формулами геометрии и на его поверхности нетрудно решать различные геодезические задачи. Самые большие отклонения реальной физической поверхности Земли от хорошо подобранного эллипсоида не превышают восемь – девять километров (пики высочайших вершин), в среднем же они не больше сотен метров на континентах и десятков метров на океанах.
Эти данные требовали некоторой идеализации формы Земли. Практические данные показали, что Земля – геоид, который определяется как средняя поверхность моря.
Чтобы понять, как выглядит поверхность геоида на материках, надо вообразить себе, что через материки прорыты каналы, и вода в них стоит на уровне моря. Форма геоида зависит также от гравитационного притяжения Земли. О том, что ускорение свободного падения повсюду на Земле примерно одинаково, свидетельствует форма геоида и его почти гладкая поверхность.
В конце прошлого столетия было введено понятие геоида как геометрической фигуры, представляющей Землю. За геоид принимается уровень поверхности, которая совпадает с поверхностью воды в океанах, если отсутствуют волны, ветровой надув и прочие возмущающие явления. В районе континентов эта поверхность проходит под сушей. Вообще уровенной поверхностью называется поверхность равного потенциала силы тяжести (работы, совершаемой единичной массой при переносе её из безконечности в данную точку или на данную поверхность). Линии действия сил всегда перпендикулярны уровенной поверхности, и поэтому жидкость на ней находится в равновесии и не должна перетекать. Геоид как уровенная поверхность почти точно совпадает с поверхностью Земли на океанах и отклоняется от неё на континентах, и это отклонение тем больше, чем больше возвышается континент над уровнем моря. Учёные ввели понятие геоида как третье, более точное приближение к фигуре Земли по сравнению с шаром и эллипсоидом».
«Геоид – эквипотенциальная поверхность (геометрическое место точек равных потенциалов) земного поля тяжести, приблизительно совпадающая со средним уровнем вод Мирового океана в невозмущённом состоянии и условно продолженная под материками.
Геоид по форме больше похож на грушу, чем на шар. Форму геоида можно узнать только с помощью обширных гравитационных измерений и расчётов. Структура распределения тяготеющих масс Земли влияет на форму геоида. С геоидом связана система астрономических координат, с эллипсоидом вращения – система геодезических координат» (Википедия).
Получается, что геоид – это такая форма Земли, которая даст возможность понять, как Земля связана с окружающим её космическим пространством и с объектами, находящимися в нём.
В чём значение геоида для самой Земли, как её формы?
«Геоид является поверхностью, относительно которой ведётся отчёт высот над уровнем моря, в силу чего знание параметров геоида необходимо, в частности, в навигации – для определения высоты над уровнем моря на основе геодезической (эллипсоидной) высоты, измеряемой GPS – приёмниками, а также в физической океанологии – для определения высот морской поверхности.
Высота над уровнем моря – мнимая мера разности потенциалов в точке земной поверхности и в начале счёта высот. В исходном пункте высота принимается равной нулю.
Навигация – определение местоположения, скорости и ориентации движущихся объектов.
Уровень моря – положение свободной поверхности Мирового океана, измеряемое по отвесной линии относительно некоторого условного начала отсчёта.
Океанология или океанография изучает крупномасштабное взаимодействие океана и атмосферы и его длинноприродную изменчивость, химический обмен океана с материками, атмосферой и дном, биоту (исторически сложившаяся совокупность видов организмов) и её экологические взаимодействия.
Исследования с использование изменяющегося во времени геоида, рассчитанные по данным GRACE, позволили получить информацию о глобальных гидрологических циклах, балансах массы ледниковых щитов и гляциозостазии (очень медленные горизонтальные и вертикальные движения земной поверхности на территориях древнего и современного оледенения). Данные экспериментов GRACE также могут использоваться для определения вязкости мантии Земли» (Википедия).
Для чего это нужно человечеству? Для того, что понять механизм смены полюсов Земли, а, следовательно, суметь пережить очередной глобальный катаклизм. Из древних учений следует, что такие катаклизмы происходят примерно каждые 6000 лет, чередуясь огненным и водным.
«В отличие от эллипсоида, геоид ближе к реальной фигуре Земли и совпадает с ней. Теория геоида подтверждается эмпирическими следствиями. При геодезических измерениях горные породы, обладающие сравнительно большей массой, чем их окружающая среда, отклоняют отвес от центра Земли и притягивают к себе. При этом отвес отклоняется от расчётного направления на центр тяжести эллипсоида, совпадая с направлением на местный центр тяжести. Последнее перпендикулярно истинной горизонтальной плоскости, касательно к поверхности геоида, поэтому плоскость, касательная к поверхности эллипсоида, является мнимой.
Земля имеет слегка грушевидную форму, причём «черенок груши» располагается у северного полюса. Грушевидность частично объясняется существованием пары, расположенных в противоположных направлениях гравитационных «впадин» в северном и южном полушариях. Глубина этих впадин достигает семидесяти пяти метров».
Необходимо заметить, что изменения во взглядах на форму Земли происходили с усложнением самой формы, причём предыдущий взгляд становился часть последующего.
«Известно, что познающий субъект на каждом историческом отрезке развития общества ограничен в воспроизведении мира. Окружающий мир безконечен и никогда не может быть познан полностью».
То есть представление о форме Земли будет развиваться и усложнятся и дальше, по мере эволюции самого человечества.
«Но важно и другое. Познавательный образ, воспринимаемый зрительно, в некотором роде богаче, чем объективная действительность и практика, в ходе которой он возникает.
Теория, как правило, развивается, уточняется, проходит через горнило острых противоречий дискуссий, тем самым она всё более приближается к истине. И в этих условиях она не должна покидать реалистическую почву, ибо из всех видов информации только логическая информация и связанные с ней принципы рационализма, как метода познания могут достаточно аргументировано претендовать не только на описание, но и логическое объяснение происходящего вокруг нас».