как перевести комплексное число в алгебраическую форму
Комплексные числа
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Вычислить сумму и разность заданных комплексных чисел:
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
Аналогично выполним вычитание чисел:
Выполнить умножение и деление комплексных чисел:
Так, теперь разделим первое число на второе:
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
Для возведения в квадрат достаточно умножить число само на себя:
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
Найдем чем равен аргумент:
$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$
Записываем в тригонометрическом виде:
Преобразуем в алгебраическую форму для наглядности:
Представим число в тригонометрической форме. Найдем модуль и аргумент:
Используем знакомую формулу Муавра для вычисления корней любой степени:
Как перевести комплексное число в алгебраическую форму
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
где r =| z | — модуль комплексного числа, а угол 
Пример 7.1. Записать комплексные числа 
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Как перевести комплексное число в алгебраическую форму
Геометрическая интерпретация комплексного числа – точка (или вектор) на плоскости.
По оси абсцисс расположена ось действительных чисел (положительное направление обозна 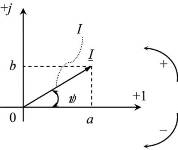
Проекция вектора на ось +1 – действительная часть, а проекция на ось +j – мнимая часть. Таким образом, алгебраическая форма записи соответствует декартовой (прямоуг ольной) системе координат (обозначим её xy).
Этот же вектор м ожет быть задан и в полярной системе координат. То есть через длину вектора I и угол поворота ψ (обозначим её rθ). Полярной системе координат соответствует показательная форма записи комплексного числа
где I – модуль комплексного числа; ψ – аргумент (или попросту угол)
Обе формы записи (алгебраическая и показательная) используются при расчётах: складывать и вычитать комплексные числа удобно в алгебраической форме записи, а делить и умножать – в показательной. Следовательно, нужно уметь переводить комплексные числа из алгебраической формы записи в показательную (→rθ) и из показательной в алгебраическую (→xy).
Основные операции с комплексными числами
Сложение
Пусть два комплексных числа заданы в алгебраической форме записи
То есть при сложении действительные части складываются с действительными, а мнимые с мнимыми.
Вычитание – аналогично:
Умножение
Пусть два комплексных числа заданы в показательной форме записи
То есть при умножении модули перемножаются, а аргументы складываются
Деление
Пусть два комплексных числа заданы в показательной форме записи
То есть при делении модули делятся, а аргументы вычитаются.
Операции с комплексными числами на инженерных калькуляторах
Первое на что нужно обратить внимание при включении калькулятора это, в каких единицах измеряются углы.
Как преобразовать показательную форму записи величины в алгебраическую
В общем случае алгебраическая форма записи комплексной величины выглядит следующим образом:
Но это математическая запись. В электротехнике принято мнимую единицу обозначать не «i», а буквой «j» (это сделано для того, чтобы не было путаницы с токами, которые чаще всего и обозначаются латинской буквой «i»). Тогда в электротехнике вы скорее всего увидите запись:
При этом мнимая единица может стоять как первым множителем, так и вторым. То есть это же число можно записать:
Что касается показательной формы записи, то в она обычно выглядит так:
Чтобы легко понять как эти формы записи связаны друг с другом, достаточно рассмотреть изображение вектора на комплексной плоскости:
Отсюда действительная часть комплексного числа:
Значит, мнимая часть комплексного числа:
Разберем пример. Пусть задано напряжение в показательной форме:
Определим действительную часть алгебраической формы записи:
Теперь мнимую часть:
В качестве итога, запишем алгоритм перевода показательной формы записи комплексного числа в алгебраическую:
1.Перевод комплексного числа из одной формы в другую. Как показано выше, комплексное число можно записать в одной из трех форм:
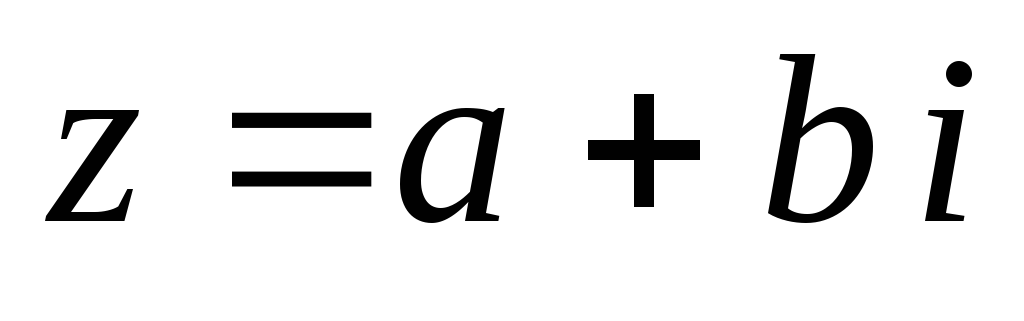

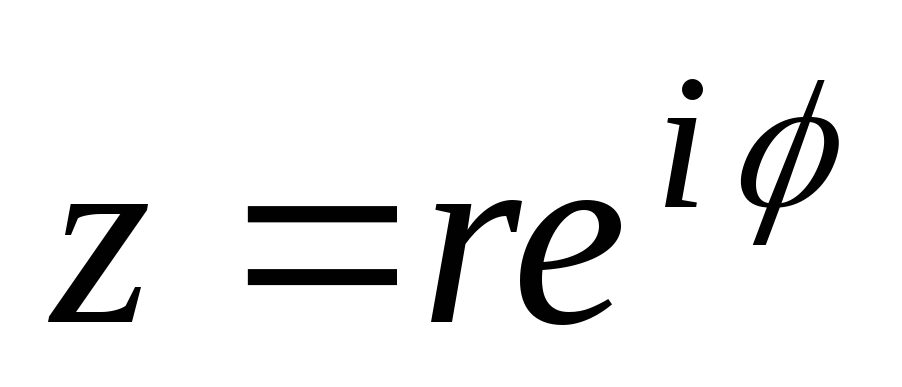
А) Перевод из алгебраической формы в тригонометрическую и показательную
Построить вектор – геометрическое изображение комплексного числа.
Отметить на чертеже острый угол от вектора до ближайшей к нему части оси Ox и угол – от положительной части оси Ox до вектора.
Вычислить модуль 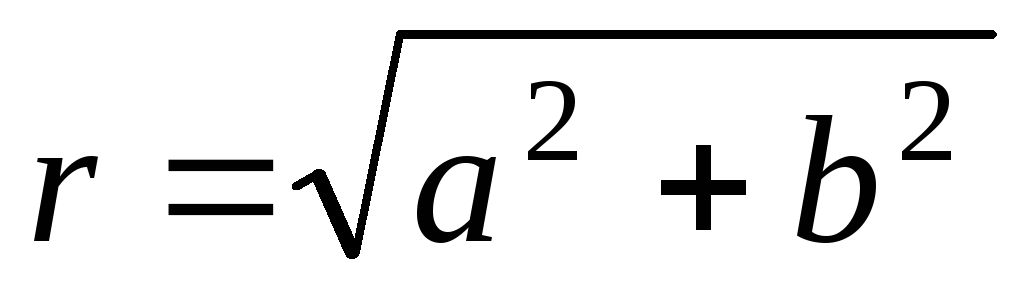
Вычислить 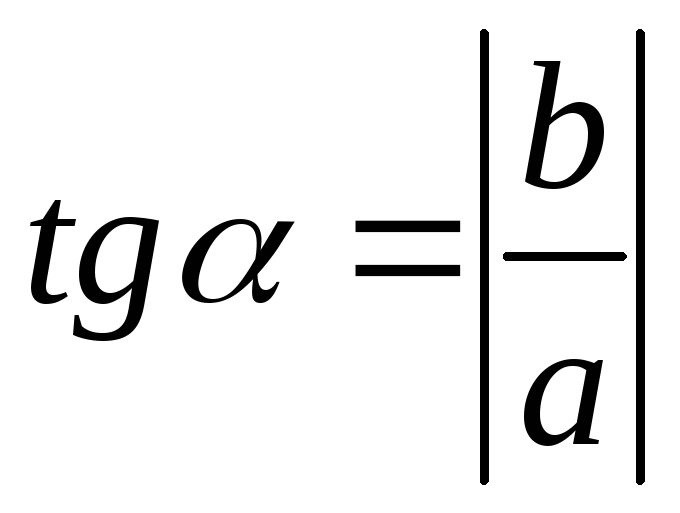
По найденному значению и чертежу определить аргумент .
Подставить найденные значения модуля и аргумента в запись тригонометрической и показательной форм.
Пример. Записать в тригонометрической и показательной формах комплексное число 
На чертеже построен вектор и отмечены углы и .
М


Из чертежа видно, что = 180 – = 150. Поэтому 
б) Перевод комплексного числа из тригонометрической формы в алгебраическую
Вычислить синус и косинус.
Раскрыть скобки.Пример.Записать комплексное число 
Р 
в) Перевод комплексного числа из тригонометрической формы в показательную и наоборот. В обеих формах комплексное число определяется модулем и аргументом. Поэтому алгоритм перевода состоит из одного действия:
Переписать в нужной форме.Пример.Записать комплексное число 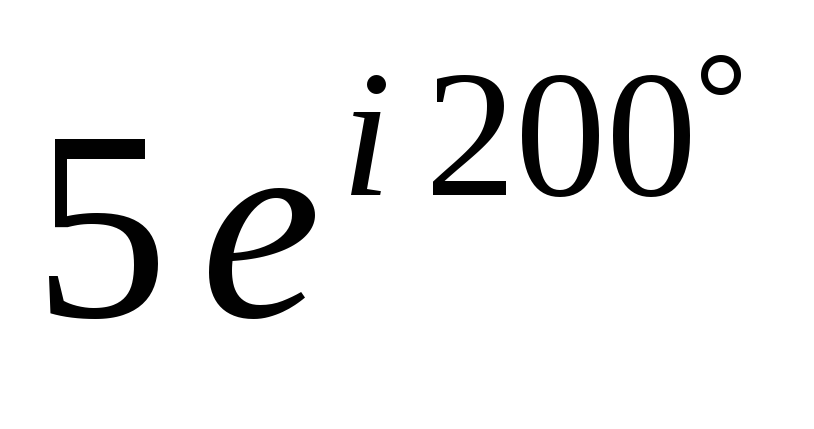
Решение.Из записи числа видно, что его модуль r = 5 и аргумент = 200. Поэтому тригонометрическая форма числа имеет вид
г) Перевод из комплексного числа показательной формы в алгебраическую.
Выше описан перевод комплексного числа из показательной формы в тригонометрическую и из тригонометрической в алгебраическую. Поэтому алгоритм имеет вид:1.Выполнить требуемый перевод через тригонометрическую форму.
2. Раскрытие неопределенности. При вычислении некоторых пределов возникает ситуация, которую называют неопределённостью. Например, если f(n) 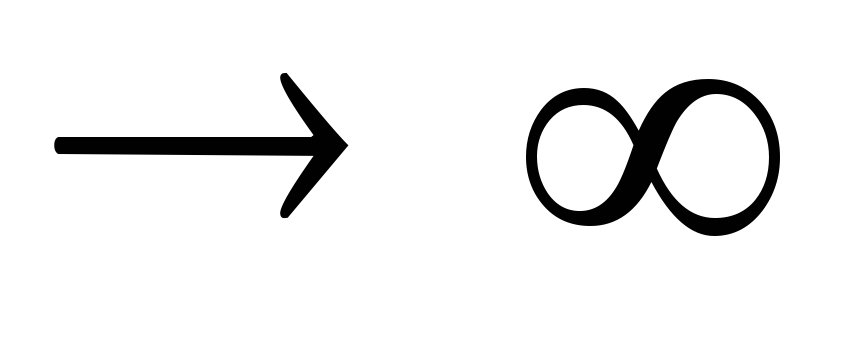




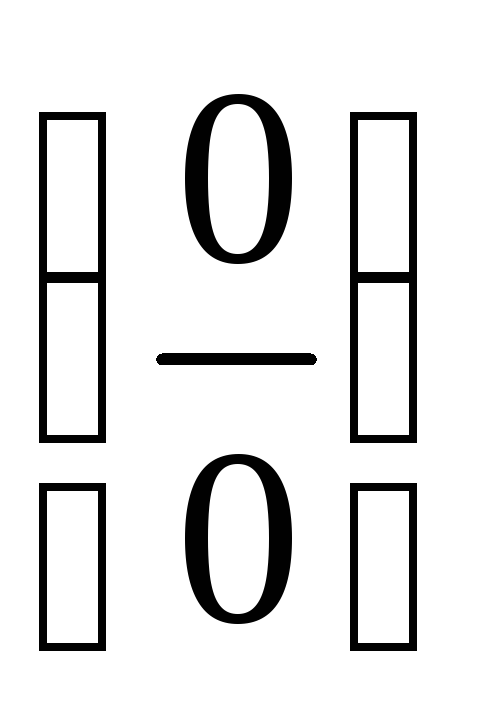








Неопределенность типа 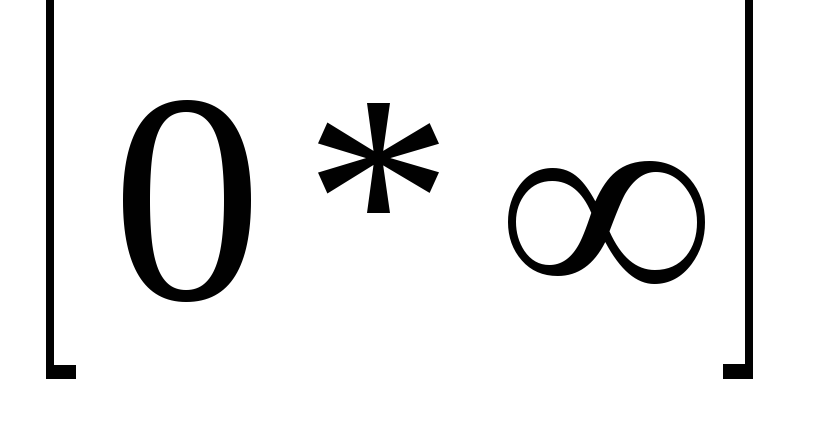
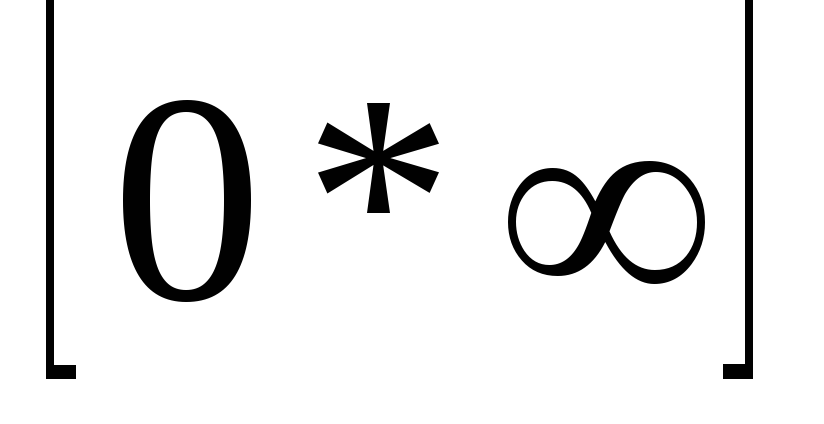

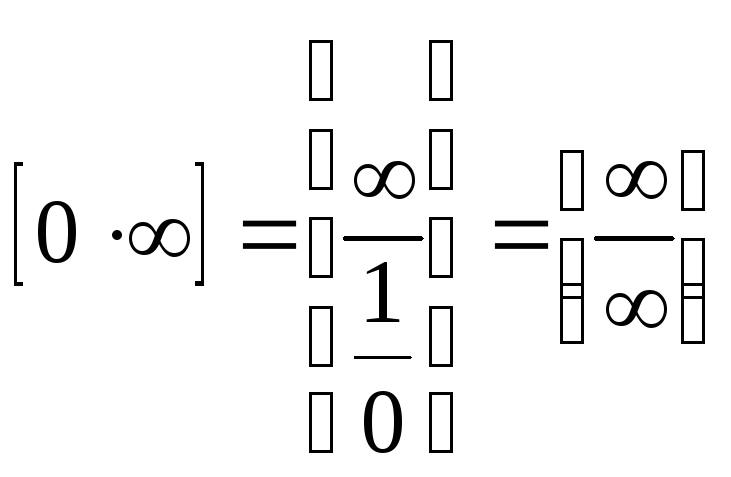
1. Под числовой последовательностью 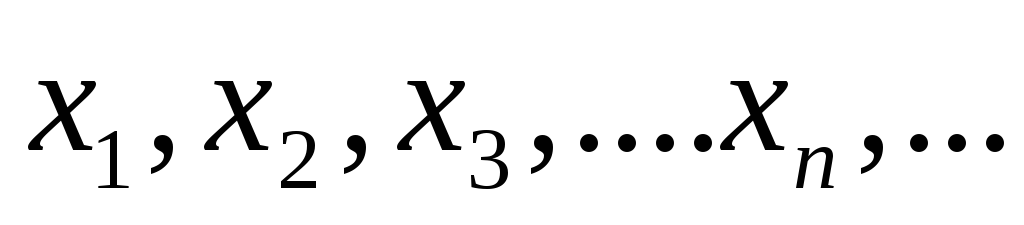



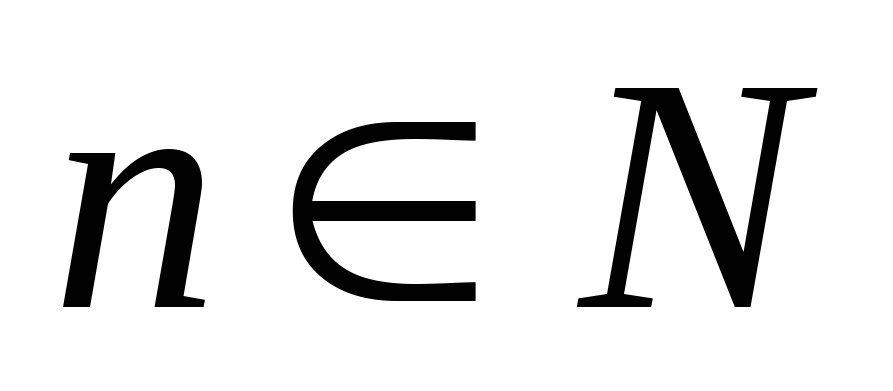



2. Формула корней квадратного уравнения с отрицательным дискриминантом.



















