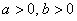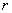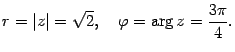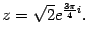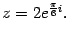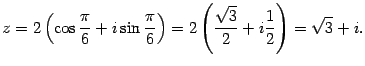как перевести комплексное число в экспоненциальную форму
Как перевести комплексное число в экспоненциальную форму
Глава 3. Работа с векторами и матрицами
MathCAD с одинаковым успехом вычисляет выражения с действительными и комплексными числами.
Комплексные числа можно записывать в любой принятой в математике форме:
– обычной (в виде суммы действительной и мнимой частей числа) – с=а+ b · i ;
– в тригонометрической форме – c = A ·( sin ( φ )+ i · cos (φ));
Для ввода мнимой единицы надо набрать с клавиатуры 1 i или 1 j и ввести число. При выведении курсора из области числа символ 1 исчезает, остается комплексное число в привычном виде (рис. 3.23 ).
расчет токов в цепи по уравнениям Кирхгофа ORIGIN:=1
Рис. 3. 23 Ввод комплексных чисел
Расчет напряжений по закону Ома 
без оператора векторизации выведено скалярное произведение векторов
это не аргумент функции—без вывод комплексно-сопряженных чисел
оператора векторизации не обойтись
Рис. 3. 24 Расчеты с векторами комплексных чисел
Модуль комплексного числа 
вычисляется оператором || вводимым с панелей Calculator (Калькулятор) или Matrix (Матрица). Тот же оператор позволяет вычислить модуль вектора или определитель матрицы.
Аргумент комплексного числа вычисляется по формуле встроенной функцией arg ( A ), которая выдает угол поворота вектора в системе координат Re – Im (рис. 3.25 ).
модуль комплексного числа. необходим оператор векторизации
аргумент комплексного числа
угол в радианах угол в градусах
Рис. 3. 25 Вычисление модуля и аргумента комплексных чисел
Как преобразовать комплексное число из алгебраической формы в экспоненциальную форму и наоборот. Приведите пример
С алгебраической формой комплексного числа мы уже познакомились,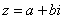 
– это и есть алгебраическая форма комплексного числа.
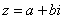
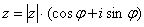
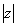
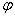
Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:
, где 
– это модуль комплексного числа, а 
– аргумент комплексного числа. Не разбегаемся, всё проще, чем кажется.
Изобразим на комплексной плоскости число 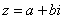. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что 
Модулем комплексного числа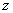 
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.
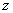
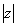
Модуль комплексного числа стандартно обозначают: или 
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: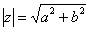 
. Данная формула справедлива для любых значений «а» и «бэ».
Пример 17.7 Пусть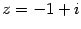 
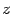
. Напишите показательную форму числа 
.
Решение. Находим модуль и аргумент числа:
Следовательно, показательная форма комплексного числа такова:
Пример 17.8 Комплексное число записано в показательной форме
Найдите его алгебраическую форму.
Решение. По формуле Эйлера
Итак, алгебраическая форма числа: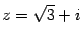 
.
Распечатайте эти вопросы и запишите присланный регистрационный номер в левый верхний угол титульного листа.
Защищать работу можно у любого преподавателя кафедры «Высшая математика».
Расписание консультаций расположено в 7 корпусе рядом с аудиторией 7-310.
Как перевести комплексное число в экспоненциальную форму
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
называются комплексно сопряженными.
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
, изображающего комплексное число z = x + iy (см. рис. 7.1). Тогда из соотношений сторон в прямоугольном треугольнике получаем
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
можно записать в так называемой показательной (или экспоненциальной) форме
где r =| z | — модуль комплексного числа, а угол 
( k =0;–1;1;–2;2…).
Пример 7.1. Записать комплексные числа 
в тригонометрической и показательной формах.
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
на число, сопряженное знаменателю, с дальнейшим применением равенства i 2 = –1 и формулы разности квадратов.
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Введение в комлексные числа
Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.
А школьники могут что-то новое узнать 😉
// Всех кого заинтересовал прошу под кат.
Итак, комплексные числа эта такие числа, которые можно записать как
Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство
x называется действительной частью, y — мнимой.
Это алгебраическая форма записи комплексного числа.
Существует также тригонометрическая форма записи комплексного числа z:
С введением, пожалуй, все.
Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.
У нас есть два таких комплексных числа:
Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:
Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число
Умножение выполняется вот так:
Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:
Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:
Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.
UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 😉
Комплексные числа
 Алгебраическая форма записи комплексных чисел |
| Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
| Комплексно сопряженные числа |
| Модуль комплексного числа |
| Деление комплексных чисел, записанных в алгебраической форме |
| Изображение комплексных чисел радиус-векторами на координатной плоскости |
| Аргумент комплексного числа |
| Тригонометрическая форма записи комплексного числа |
| Формула Эйлера. Экспоненциальная форма записи комплексного числа |
| Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
| Извлечение корня натуральной степени из комплексного числа |
Алгебраическая форма записи комплексных чисел
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Комплексно сопряженные числа
|  |
|  |
|  |
|  |
|  |
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
|  |
|  |
|  |
|  |
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Считается, что комплексное число нуль аргумента не имеет.
Тогда оказывается справедливым равенство:
 | (3) |
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры |  |
значение
аргумента
значение
аргумента
значение
аргумента
x z
квадрант
x z
мнимая
полуось
y z
квадрант
Положительная вещественная полуось
Главное значение аргумента:
Расположение числа z :
Главное значение аргумента:
Расположение числа z :
Положительная мнимая полуось
Главное значение аргумента:
Расположение числа z :
Главное значение аргумента:
Расположение числа z :
Отрицательная вещественная полуось
Отрицательная мнимая полуось
x z = x + i y может быть записано в виде
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 
и 
записанных в экспоненциальной форме, осуществляется по формулам
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня натуральной степени из комплексного числа
Пусть 
— произвольное комплексное число, отличное от нуля.
Для того, чтобы решить уравнение (8), перепишем его в виде
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
то по формуле (10) получаем:
