как понять левый или правый дирекционный угол
Дирекционный угол
Приближенные значения дирекционных углов направлений с точностью порядка 10-25 угловых минут могут быть вычислены из значения магнитного азимута направления, который определен с помощью ориентир-буссоли, которая входит в комплект дополнительного оборудования теодолитов и тахеометров. Ориентир-буссоль предназначена для определения магнитных азимутов направлений. Для перехода от магнитного азимута к дирекционному углу необходимо знать поправку буссоли (ПБ), которая определяется, как правило, на исходном геодезическом пункте в районе выполнения работ.
Дирекционный угол направления на ориентир может быть вычислен путём решения обратной геодезической задачи если известны плоские прямоугольные координаты исходной точки и ориентира.
Дирекционные углы направлений могут быть измерены с точностью порядка 30-60 угловых минут по топографической карте с помощью транспортира. При измерениях дирекционных углов по топографической карте можно использовать следующее определение дирекционного угла: дирекционным углом ɑ называется горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360°, между северным направлением вертикальной линии километровой сетки плоских прямоугольных координат и направлением на ориентир.
Дирекционный угол направления может быть приблизительно с точностью порядка 0.5-3 угловых градуса определен на местности по значению магнитного азимута направления измеренного с помощью компаса путём ввода в измеренное значение магнитного азимута поправки направления (ПН), взятой с топографической карты на дату наблюдений.
Связанные понятия
Геодези́ческой (эллипсоида́льной) высото́й некоторой точки физической поверхности земли называется отрезок нормали к эллипсоиду от его поверхности до данной точки. Вместе с геодезическими широтой и долготой (B и L соответственно) она определяет положение точки относительно заданного эллипсоида. Физически эллипсоида не существует, следовательно геодезическая высота не может быть непосредственно измерена наземными методами. Определить её возможно с помощью спутниковых измерений, а также посредством.
Дирекционные углы смежных линий
Дирекционные углы смежных линий изображены на рисунке:
Для линии AB смежной явлется линия BC, тогда αA-B дирекционный угол линии AB, а αB-C это дирекционный угол смежной линии BC.
Между дирекционными углами смежных линий можно установить связь, если известен угол β при общей точке B.
Угол β измеряется на местности теодолитом, причем если двигаться по направлению A-B-C, тогда угол β который окажется по левую руку считается левым (βлев), а по правую руку – правым (βпр). Двигаясь в обратном направлении (C-B-A), правый угол становится левым, а левый сответственно правым, поэтому при расчетах необходимо быть внимательным.
Зная дирекционный угол одной из линий и угол β между этими линиями, можно вычислить дирекционный угол другой линии, используя формулы:
При вычислении по этим формулам дирекционный угол смежной линии может получиться или меньше нуля (отрицательным) или превышать 360°, тогда к нему соответственно прибавляют или от него отнимают 360°.
Примеры вычисления дирекционных углов смежных линий
Пример 1: вычислить дирекционный угол смежной линии BC, если дирекционный угол линии AB равен 75°57′ и угол β = 68°14′.
двигаясь по направлению A-B-C угол β является правым, тогда используя формулу можем записать:
Пример 2: вычислить дирекционный угол смежной линии BA, если дирекционный угол линии CB равен 270°05′ и угол β = 290°14′:
двигаясь по направлению C-B-A угол β является левым, тогда используя формулу можем записать:
дирекционный угол получился больше 360°, поэтому из его значения отнимаем 360°
Тема: Основы математической обработки результатов теодолитной съёмки. Вычисление координат вершин теодолитного хода. Составление плана
1. Проверка полевых вычислений и определение поправок в измерения длин линий
_______ Далее вычисляются средние значения длин линии:
 |
_______ В каждую длину линии вводятся поправки по формуле:
 |
_______ Поправки вводятся при:
 |
_______ После уравнивания углов производится вычисление дирекционных углов всех сторон теодолитного хода. _______ Вычисленные дирекционные углы переводятся в румбы.
2. Связь между дирекционными углами и горизонтальными углами теодолитного хода
 |
 |
_______ Дирекционный угол линии последующей равен дирекционному углу линии предыдущей плюс 180 0 минус угол вправо по ходу лежащий.
3. Обработка угловых измерений замкнутого теодолитного хода
 |
 |
_______ где fβ – угловая невязка.
 |
_______ где n –вершина углов, следовательно:
 |
4. Угловая невязка разомкнутого теодолитного хода
 |
Для вычисления ∑β теор. найдем дирекционные углы всех сторон хода:
 |
 |
 |
 |
_______ где αнач. и αкон. – дирекционные углы сторон опорной сети, тогда:
 |
5. Невязки в диагональном ходе
 |
 |
_______ После обработки угловых измерений вычисляются дирекционные углы и румбы всех сторон хода.
6. Прямая и обратная геодезические задачи
6.1. Прямая геодезическая задача: по координатам отрезка прямой (начала), его длине и направлению определить координаты конца отрезка
 |
 |
_______ Прямая геодезическая задача применяется при вычислении координатных точек теодолитного хода.
6.2. Обратная геодезическая задача: по координатам начала и конца отрезка прямой найти его длину и направление
 |
 |
_______ Далее вычисляют arctg и находят числовое значение румба. Название румба определяют по знакам приращений координат, от румба переходят к дирекционному углу.
Длина линии может быть найдена по следующим формулам:
 |
_______ Обратная геодезическая задача применяется при подготовке данных для перенесения проектов сооружений в натуру.
7. Уравнивание приращений координат
_______ Уравниванием называется совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений.
_______ Уравнивание проводится для устранения невязок, обусловленных наличием ошибок в избыточно измеренных величинах, и для определения вероятнейших значений искомых неизвестных или их значений, близких к вероятнейшим. В процессе уравнвиания это достигается путём определения поправок к измеренным величинам (углам, направлениям, длинам линий или превышениям).
7.1. Вычисление координат точек теодолитного хода
 |
_______ Из решения прямой геодезической задачи по известным длинам сторон и румбам вычисляются приращения координат для каждой стороны хода по формулам:
 |
_______ Далее вычисляются невязки в приращениях координат замкнутого хода.
7.2. Вычисление невязок в приращениях координат замкнутого хода
_______ Из геометрии известно, что сумма проекций сторон многоугольника на любую ось равна нулю, следовательно:
 |
_______ Под влиянием ошибок измерений замкнутый полигон будет разомкнутым на величину fр – абсолютная невязка в периметре полигона.
 |
 |
_______ Если полученная невязка недопустима, то необходимо произвести повторное измерение длин линий.
_______ Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме – в данном случае равна нулю.
7.3. Вычисление невязок в приращениях координат разомкнутого теодолитного хода
_______ Определение допустимости невязок и их распределения производится так же, как для замкнутого теодолитного хода.
 |
 |
Для диагонального хода, например:
 |
 |
_______ По исправленным значениям приращений координат вычисляются координаты всех точек хода по формулам:
 |
8. Построение плана
_______ Построение плана выполняются в следующей последовательности :
1) построение координатной сетки,
2) нанесение вершин теодолитного хода по координатам,
3) нанесение на план контуров местности,
4) оформление плана.
8.1. Построение координатной сетки
_______ 1) построение сетки с помощью линейки Дробышева:
 |
_______ Построение сетки основано на построении прямоугольного треугольника с катетами 50×50 см и гипотенузой 70,711 см ;
2) построение сетки с помощью циркуля, измерителя и масштабной линейки:
 |
_______ Вершины теодолитного хода наносятся на план по координатам относительно сетки с помощью измерителя и поперечного масштаба.
_______ Контроль правильности построения точек выполняется по известным расстояниям между точками. Допустимое расхождение – 0,3 мм в масштабе плана.
_______ Контуры местности наносятся на план в соответствии с абрисами.
_______ Оформление плана выполняется в строгом соответствии с условными знаками, установленными для данного масштаба.
Измерение горизонтальных углов
Горизонтальным углом между двумя направлениями называется угол, вершиной которого является точка стояния, а сторонами – проекции на горизонтальную плоскость, проходящую через точку стояния, направлений с точки стояния на точки визирования (рис. 15.9).
Измерение горизонтальных углов теодолитами серии Т30 может выполняться двумя способами:
— способом приемов (другие названия: способ отдельного приема, способ отдельного угла); применяется для измерения отдельных углов при прокладывании теодолитных ходов, выносе проектов в натуру и т.д.
— способом повторений; применяется для измерения углов, когда необходимо повысить точность окончательного результата измерения путем ослабления влияния погрешностей отсчитывания.
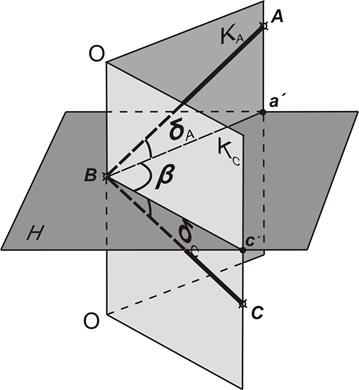 |
Рисунок 15.9 – К понятию горизонтального и вертикального углов: 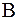 — точка стояния; — точка стояния; 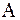 и и 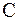 — точки визирования; — точки визирования; 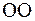 — отвесная линия; — отвесная линия; 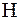 — горизонтальная плоскость; — горизонтальная плоскость; 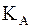 и и 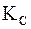 — коллимационные плоскости; — коллимационные плоскости; 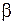 — горизонтальный угол; — горизонтальный угол; 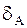 и и 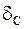 — углы наклона (вертикальные углы) — углы наклона (вертикальные углы) |
В геодезии измеряют правые и левые по ходу горизонтальные углы способом приемов. В маркшейдерском деле обычно измеряют левые по ходу углы способом приемов или повторений.
В учебной программе рассматривается только способ приемов.
Понятие «левые либо правые по ходу углы» – означает следующее.
Пусть прокладывается теодолитный ход, состоящий из нескольких точек, обозначенных, к примеру, 
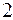
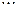

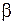

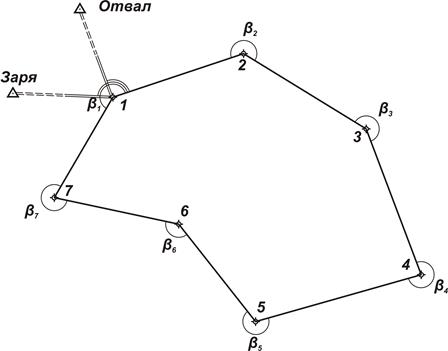 |
| Рисунок 15.10 – Схема теодолитного хода |
«Левым по ходу» углом при точке стояния называется угол, отсчитываемый по часовой стрелке от направления на заднюю точку визирования до направления на переднюю точку.
«Правым по ходу» углом при точке стояния называется угол, отсчитываемый по часовой стрелке от направления на переднюю точку визирования до направления на заднюю точку.
То, что отсчет углов в указанных выше определениях ведется именно по часовой стрелке связано с конструктивными особенностями теодолитов, а именно, лимб горизонтального круга в угломерных приборах всегда оцифровывается по часовой стрелке. По этой причине все способы и методики измерения горизонтальных углов ориентированы на измерения по часовой стрелке, даже, если вращение алидады теодолита производится при этом против часовой стрелки.
В практике, проще ориентироваться какой угол левый, а какой правый следующим образом. Если стоять на точке стояния лицом по направлению движения в ходе, то тот угол, который будет соответствовать дуге, описываемой левой рукой в направлении от задней к передней точке, будет левым, а угол, соответствующей дуге, описываемой правой рукой в направлении от задней точки к передней, будет правым.
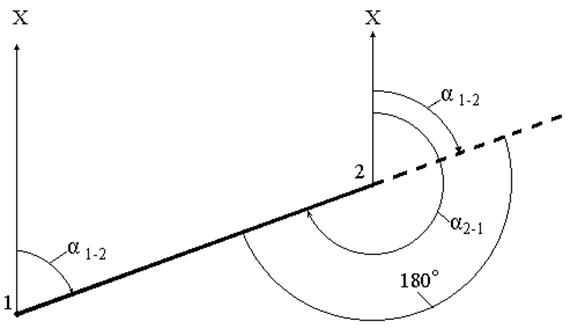
Прямые и обратные дирекционные углы
Линия, соединяющая две точки на земной поверхности, характеризуется прямым и обратным дирекционными углами. На рис. 10 показаны прямой α1-2 и обратный α2-1 дирекционные углы.
Рис.10. Прямой и обратный дирекционные углы
Эти углы, как видно из рисунка, связаны следующей зависимостью:
В общем виде зависимость между прямыми и обратными дирекционными углами записывается так
Пример. Если αпр = 200º, то α обр = 200º + 180º = 380º– 360º = = 20º, или α обр = 200º – 180º = 20º.
2.3. Связь между дирекционными углами
сторон полигона
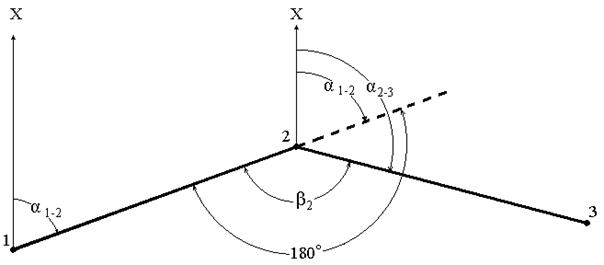
На рис. 11. показаны две стороны полигона: предыдущая 1-2 и последующая 2-3.
Рис. 11. Дирекционные углы сторон полигона
Известны дирекционный угол α1-2 и угол β2, вправо по ходу лежащий между предыдущей и последующей сторонами. Не трудно видеть, что
Дирекционный угол последующей линии равен дирекционному углу предыдущей линии плюс 180º минус угол, вправо по ходу лежащий между рассматриваемыми линиями.
Пример. Если α1-2 = 340º 12′, β2 = 145º 55′, то
α 2-3 = 340º 12′ +180º – 145º 55′ = 14º17′.
2.4. Румбы. Связь между румбами
и дирекционными углами
Румб – это острый угол между данным направлением и ближайшим направлением меридиана (северным или южным).
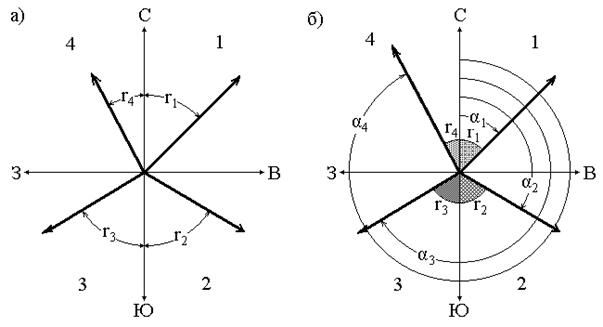
На рис. 12,а плоскость линиями С-Ю и З-В делится на четыре четверти: первая (1), вторая (2), третья (3) и четвертая (4). В первой четверти r1 = СВ:45º, во второй r2 = ЮВ:60º, в третьей r3 = ЮЗ:55º, в четвертой r4 = СЗ:30º.
Рис. 12. Румбы и дирекционные углы
На рис. 12,б видно, что
Пример. Дирекционный угол α = 133º25′. Найти соответствующий этому углу румб.
Дирекционный угол находится во второй четверти, следовательно, угловая величина румба составит 180º – 133º25′ = 46º35′. Полная запись румба r = ЮВ : 46º35′.
Дата добавления: 2015-02-23 ; просмотров: 5762 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ