как располагаются оси в прямоугольной диметрии по отношению к горизонтальной прямой

Как располагаются оси в прямоугольной диметрии по отношению к горизонтальной прямой

Контрольные задания по теме: эпюр № 6

Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.

Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:

— изометрические, когда все три коэффициента искажения одинаковы (k_x=k_y=k_z);

— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (k_x= k_z ≠k_y);

— триметрические, когда все три коэффициенты искажения не равны между собой (k_x≠k_y≠k_z).

В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в раза.

Изометрические оси изображены на рисунке 57.

Рисунок 57

Рисунок 58

Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.

Рисунок 59

Построение окружности в прямоугольной изометрической проекции

Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.

Рисунок 60

Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О₁, О₂, О₃, О₄, являющиеся центрами дуг овала (рисунок 61).

Для определения точек сопряжения проводят линии центров, соединяя О₁, О₂, О₃, О₄. из полученных центров О₁, О₂, О₃, О₄ проводят дуги радиусами R и R₁. размеры радиусов видны на чертеже.

Рисунок 61

Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).

Рисунок 62

Штриховка и изометрической проекции

Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.

Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.

По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты k_x=k_z=1, k_y=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.

Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:

На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.

Рисунок 63

Построение диметрической проекции шестиугольника

Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П₁ (рисунок 64).

Рисунок 64

Рисунок 65

Построение окружности в диметрии

В прямоугольной диметрии все окружности изображаются эллипсами,

На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).

Рисунок 66

Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).

Рисунок 67

Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П₂, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О₁, О_2, О_3, О₄ – центры дуг овала (рисунок 68).

Рисунок 68

Штриховка а прямоугольной диметрии

Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).

Рисунок 69

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Как располагаются оси в прямоугольной диметрии по отношению к горизонтальной прямой

Контрольные задания по теме: эпюр № 6

Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.

Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:

— изометрические, когда все три коэффициента искажения одинаковы (k_x=k_y=k_z);

— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (k_x= k_z ≠k_y);

— триметрические, когда все три коэффициенты искажения не равны между собой (k_x≠k_y≠k_z).

В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в 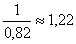раза.

Изометрические оси изображены на рисунке 57.

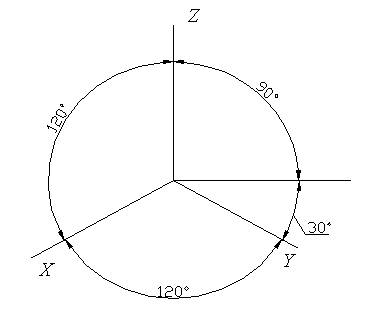
Рисунок 57

Рисунок 58

Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.

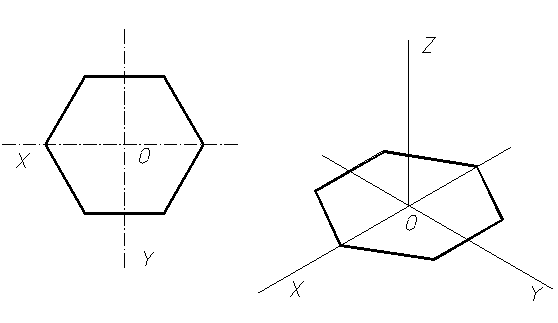
Рисунок 59

Построение окружности в прямоугольной изометрической проекции

Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.

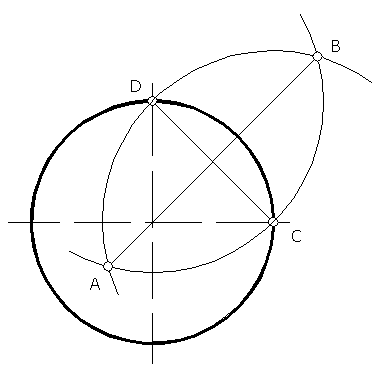
Рисунок 60

Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О₁, О₂, О₃, О₄, являющиеся центрами дуг овала (рисунок 61).

Для определения точек сопряжения проводят линии центров, соединяя О₁, О₂, О₃, О₄. из полученных центров О₁, О₂, О₃, О₄ проводят дуги радиусами R и R₁. размеры радиусов видны на чертеже.

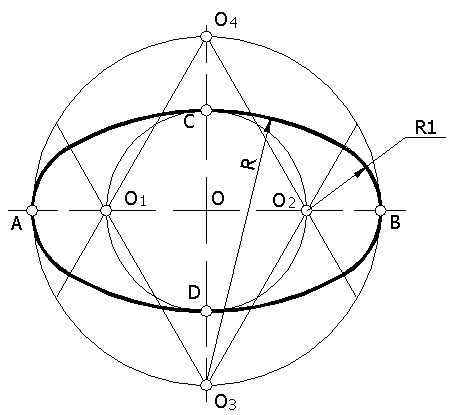
Рисунок 61

Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).

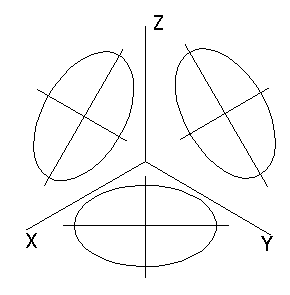
Рисунок 62

Штриховка и изометрической проекции

Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.

Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.

По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты k_x=k_z=1, k_y=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.

Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:

На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.

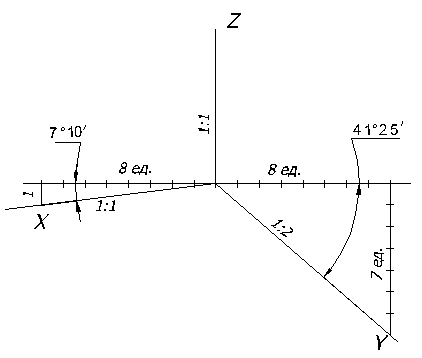
Рисунок 63

Построение диметрической проекции шестиугольника

Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П₁ (рисунок 64).

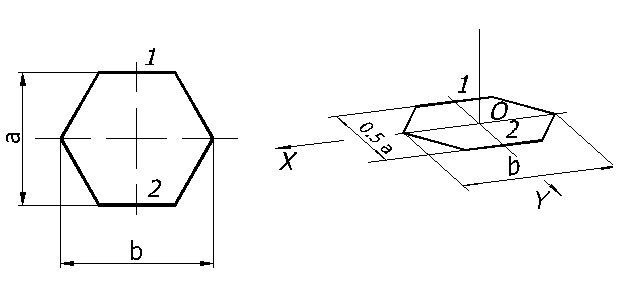
Рисунок 64

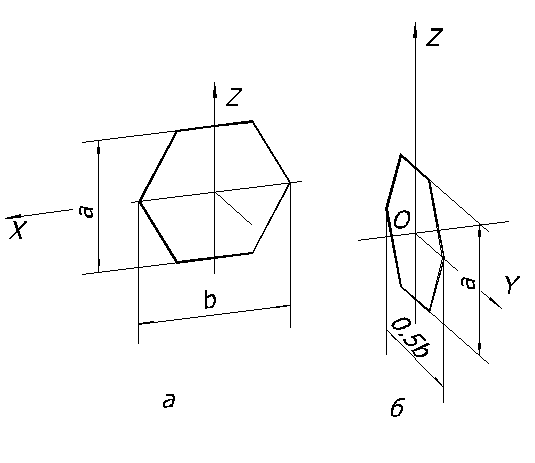
Рисунок 65

Построение окружности в диметрии

В прямоугольной диметрии все окружности изображаются эллипсами,

На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).

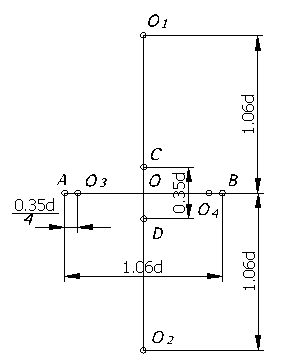
Рисунок 66

Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).

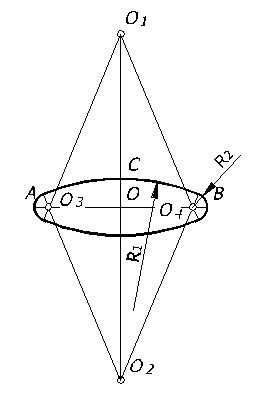
Рисунок 67

Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П₂, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О₁, О_2, О_3, О₄ – центры дуг овала (рисунок 68).

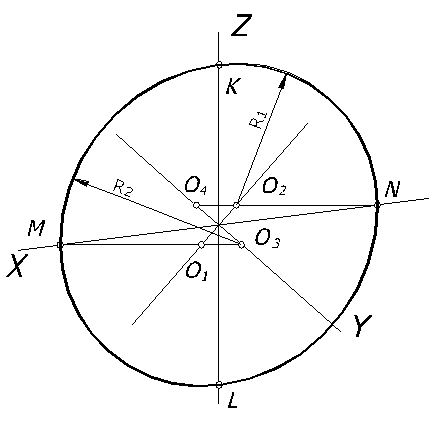
Рисунок 68

Штриховка а прямоугольной диметрии

Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).

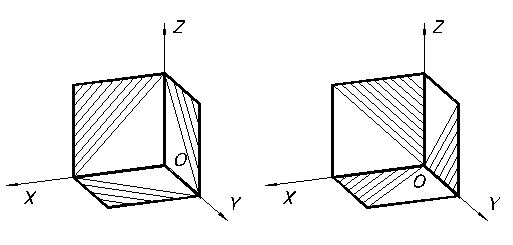
Рисунок 69

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Правила оформления чертежей Задание Вопрос Какими размерами опре. Правила оформления чертежей Задание Вопрос Какими размерами определяются форматы чертежных листов

Правила оформления чертежей

Вопрос 1. Какими размерами определяются форматы чертежных листов?

4) Размерами внешней рамки, выполняемой сплошной тонкой линией;
Вопрос 2. Где располагается основная надпись чертежа по форме 1 на чертежном листе?

5) В правом нижнем углу, примыкая к рамке формата.
Вопрос 3. Толщина сплошной основной линии в зависимости от сплошности изображения и формата чертежа лежит в следующих пределах?

2) 1:1; 1:2; 1:2,5; 1:4; 1:5; 2:1; 2,5:1; 4:1; 5:1.

Вопрос 1. Размер шрифта h определяется следующими элементами?

2) Высотой прописных букв в миллиметрах;
Вопрос 2. ГОСТ устанавливает следующие размеры шрифтов в миллиметрах?

4) 1,8; 2,5; 3,5; 5; 7; 10; 14; 20.
Вопрос 3. Толщина линии шрифта d зависит от?

2) От высоты строчных букв шрифта;
Вопрос 4. В соответствии с ГОСТ 2.304-81 шрифты типа А и Б выполняются?

2) Без наклона и с наклоном около 75 0 ;
Вопрос 5. Какой может быть ширина букв и цифр стандартных шрифтов?

4) Ширина букв и цифр определяются высотой строчных букв;
Задание 3.

Вопрос 1. В каких единицах измерения указываются линейные и угловые размеры на чертежах?

1) В сотых долях метра и градусах;
В опрос 2. При нанесении размера дуги окружности (части окружности) используют следующий знак?

1) R;
Вопрос 3. На (Рис. СЗ-1) показаны шрифты правильных и ошибочных расположений размерных линий. Определите, под каким номером обозначен правильный чертеж?

5) Правильный вариант ответа №5;
В опрос 4. Определите, на каком чертеже правильно записаны размерные числа (см. Рис. СЗ-2)?

4) Правильный вариант ответа №4;
Вопрос 5.

Н а каком чертеже правильно нанесены величины диаметра и квадрата (см. Рис. СЗ-3)?

3) Правильный вариант ответа №3;

Вопрос 1. Какими линиями выполняют вспомогательные построения при выполнении элементов геометрических построений?

2) Сплошными тонкими;
Вопрос 2. На каком расстоянии от контура рекомендуется проводить размерные линии?

1) Не более 10 мм;
Вопрос 3. На каком расстоянии друг от друга должны быть параллельные размерные линии?

1) Не более 7 мм;
Вопрос 4. Чему должен быть равен раствор циркуля при делении окружности на шесть равных частей?

5) Радиусу окружности.
В опрос 5. В каком случае показано правильное расположение центровых линий окружностей (см. Рис. СЗ-4)?

5) Правильный вариант ответа №5;

Вопрос 1. В каком месте должна находиться точка сопряжения дуги с дугой?

2) На линии, соединяющей центры сопряжений дуг;
Вопрос 2. Уклон 1:5 означает, что длина одного катета прямоугольного треугольника равна?

5) Одной единице, а другого пяти.
Вопрос 3. Какие проставляются размеры при выполнении чертежа в масштабе, отличном от 1:1?

5) Размеры должны быть увеличены или уменьшены в соответствии с масштабом.
Вопрос 4. Конусность 1:4 означает, что?

Вопрос 1. Точка может быть однозначно определена в пространстве, если она спроецирована?

4) На три плоскости проекций;
Вопрос 2. Как расположена в пространстве горизонтальная плоскость проекций? Координатного треугольника?

4) Параллельно плоскости V;
Вопрос 3. Профильная плоскость проекций для координатного трехгранника вводится?

5) Перпендикулярно плоскостям Н и V.
Вопрос 4. Трехгранный комплексный чертеж образуется?

3) Поворотом плоскости Н вниз, а плоскости W вправо на 90 0 ;
Вопрос 5. Линия связи на трехкартинном комплексном чертеже, соединяющая горизонтальную и фронтальную проекции точек, проходит?

4) Под углом 90 0 к оси x;

Вопрос 1. Отрезок общего положения в пространстве расположен?

2) Перпендикулярно плоскости V;
Вопрос 3. Горизонтальная прямая или сокращенно горизонталь расположена?

1) Параллельно плоскости Н;
Вопрос 4. Сколько Вы знаете вариантов задания проекций плоскостей на комплексном чертеже?
2) Три и четыре дополнительных;
Вопрос 5. Может ли фронтально-проецирующая плоскость одновременно быть профильной плоскостью?

4) Может, если она параллельна профильной плоскости проекций W;

Вопрос 1. Для построения проекции точки в прямоугольной приведенной изометрии пользуются следующим правилом?

1) Откладывают по всем осям отрезки, равные натуральным величинам координат;
Вопрос 2. В прямоугольной приведенной изометрии проекции окружности в плоскостях, параллельных трем плоскостям координатного трехгранника будут?

3) Все три одинаковые;

Вопрос 3. Как располагаются координатные оси в прямоугольной изометрии относительно друг друга?

4) Под углами 120 0 друг к другу;
Вопрос 4. Как располагаются оси в прямоугольной диметрии по отношению к горизонтальной прямой?

Вопрос 1. Для прямой призмы число боковых сторон будет равно?

4) Числу сторон многоугольника в основании;
Вопрос 2. Чему равно расстояние между центрами эллипсов (по высоте) для прямоугольной изометрии прямого кругового цилиндра?

1) Диаметру окружности основания цилиндра;
Вопрос 3. Боковые стороны пирамиды представляют собой?

5) Треугольники.
Вопрос 4. Для определения недостающей проекции точки, принадлежащей поверхности конуса, через известную проекцию точки можно провести?

1) Образующую или окружность, параллельную основанию;
Вопрос 5. Высота конуса (расстояние от центра эллипса до вершины) в прямоугольной изометрии равна?

3) Высоте конуса (расстоянию от центра окружности до вершины) на комплексном чертеже;

Основы технического черчения.

Вопрос 1. Какое максимальное количество видов может быть на чертеже детали?

Вопрос 2. Сколько видов должно содержать изображение какой-либо конкретной детали?

3) Минимальное, но достаточное для однозначного уяснения конфигурации;

Вопрос 3. Какой вид называется дополнительным?

4) Полученный проецированием на плоскость, не параллельную ни одной из плоскостей проекций;

Вопрос 4. Что называется местным видом?

1) Изображение только ограниченного места детали;

Вопрос 5. Какой вид детали и на какую плоскость проекций называется ее главным видом?

1) Вид сверху, на плоскость Н;

2) Вид спереди, на плоскость V;

3) Вид слева, на плоскость W;

4) Вид сзади, на плоскость Н;

5) Дополнительный вид, на дополнительную плоскость.
Задание 2.

Вопрос 1. Даны два вида деталей: главный вид и вид слева. Определите вид сверху из предложенных вариантов.

3) Правильный вариант ответа №3;

В опрос 2. Определить вид слева детали по заданным главному виду и виду сверху. (см. Рис. С3-7)

4) Правильный вариант ответа №4;

Вопрос 4. Когда на чертеже делают надписи названий основных видов?

4) Когда нужно показать дополнительный вид;
Вопрос 5. Возможно ли выполнение дополнительных видов повёрнутыми?

5) Возможно, но дополнительный вид выполняется только в проекционной связи по отношению к главному.

Вопрос 3. Какие разрезы называются горизонтальными?

Вопрос 5. Какие вы знаете вертикальные разрезы?

1) Горизонтальный т фронтальный;

3) Горизонтальный и наклонный;

4) Наклонный и фронтальный;

5) Фронтальный и профильный.

Вопрос 1. Простой разрез получается при числе секущих плоскостей, равных:

2) Перпендикулярно друг другу;

Вопрос 4. Всегда ли нужно обозначать простые разрезы линией сечения?

1) Да, обязательно;
Вопрос 5. В каком случае можно соединять половину вида с половиной соответствующего разреза?

4) Если вид и разрез являются симметричными фигурами;

Вопрос 1. Если вид и разрез являются симметричными фигурами, то какая линия служит осью симметрии, разделяющей их половины?

5) Штрих-пунктирная тонкая.

Вопрос 2. Как изображаются на разрезе элементы тонких стенок типа рёбер жесткости, зубчатых колёс?

4) Показываются рассечёнными, но штрихуются в другом направлении по отношению к основной штриховке разреза;
Вопрос 3. Какого типа линией с перпендикулярной ей стрелкой обозначаются разрезы (тип линий сечения).

1) Сплошной тонкой линией;
Вопрос 4. Как проводят секущие плоскости при образовании разрезов на аксонометрических изображениях,

например, при выполнении выреза четверти детали.

2) только параллельно координатным плоскостям;

Вопрос 5. Как направлены линии штриховки разрезов на аксонометрических проекциях?

4) Параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям.

З адание 6.

Вопрос 4. На каком изображении детали правильно выполнен её разрез (рис. С3-12)?

4) На четвертом изображении;
В опрос 5. Под каким углом осуществляется штриховка металлов (графическое изображение металлов) в разрезах?

5) Под углом 75 градусов к линии основной надписи чертежа;
Задание 7.

Вопрос 3. В каком случае правильно выполнено совмещение вида с разрезом (см. Рис. С3-13)?

Вопрос 5. Всегда ли обозначается положение секущих плоскостей при сложных разрезах?

Вопрос 1. В сечении показывается то, что:

Вопрос 2. Контур вынесенного сечения выполняется:

3) Волнистой линией;

Вопрос 3. На рисунке С3-15 показана деталь и дано её сечение. Из нескольких вариантов сечения выберите правильный.

Вопрос 5. Как обозначают несколько одинаковых сечений, относящихся к одному предмету?

2) Никак не обозначают;

Вопрос 1. Дана деталь и указано ее сечение А-А (рис.С3-17-а). Выбрать правильный вариант сечения.

3) Правильный вариант ответа №3;
Вопрос 2. Дана деталь и указано ее сечение А-А (рис.С3-17-б). Выбрать правильный вариант сечения.

4) Правильный вариант ответа №4;

Вопрос 3. Дана деталь и указано ее сечение А-А (рис.С3-17-в). Выбрать правильный вариант сечения.

1 ) Правильный вариант ответа №1;

Источник