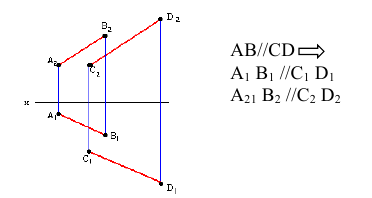
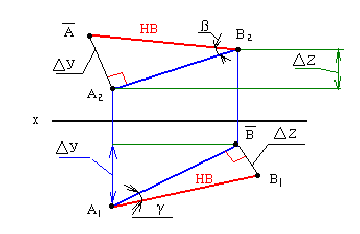
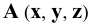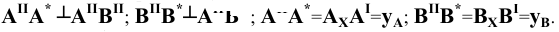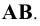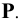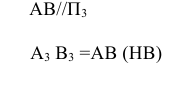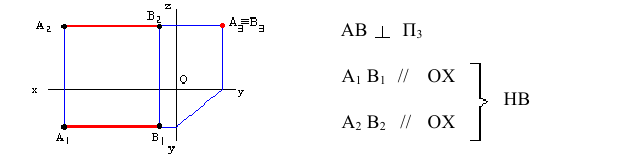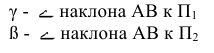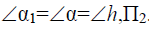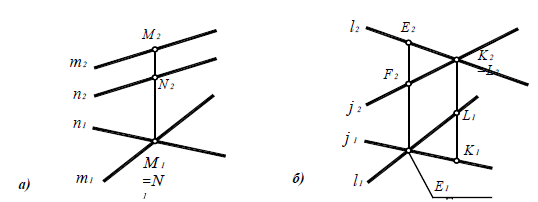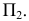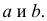как располагаются прямые уровня по отношению к плоскостям проекций
Глава 7. Изображение линий на чертежах
§ 40. Расположение прямой относительно плоскостей проекций
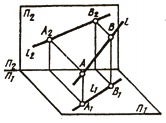
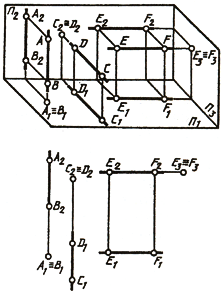
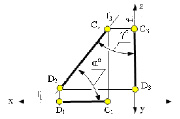
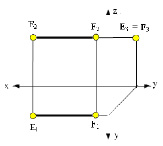
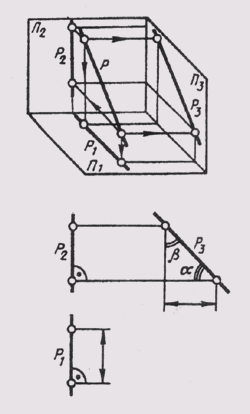
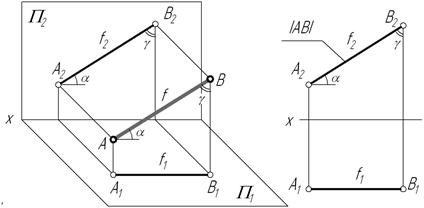
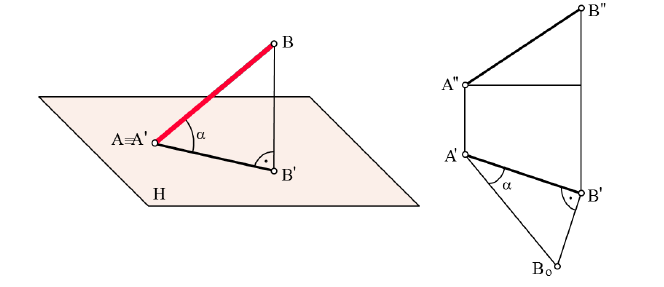
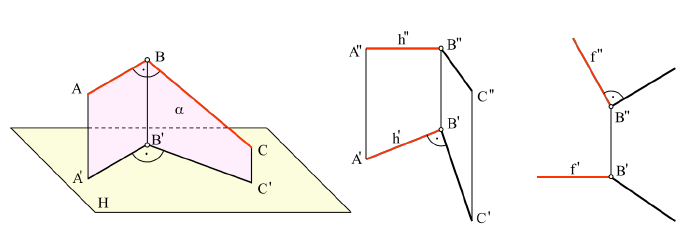
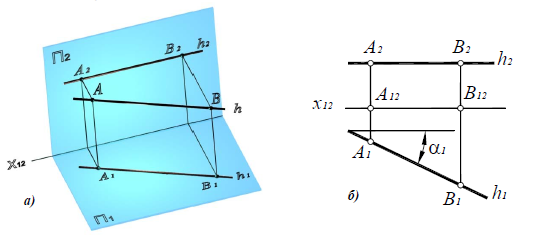
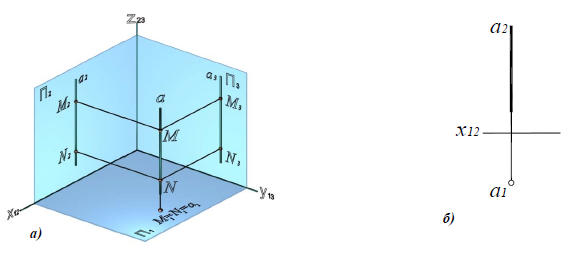
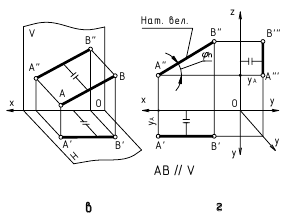
Прямую, параллельную фронтальной плоскости проекций, называют фронталью и обозначают f (рис. 71).
Прямую, параллельную профильной плоскости проекций, называют профильной и обозначают р (рис. 72).
У прямой уровня одна проекция параллельна самой прямой и определяет углы наклона этой прямой к двум другим плоскостям проекций.
Параллельность одной из плоскостей проекций определяет расположение двух других проекций прямой уровня:
Прямые h2 и f1 перпендикулярны вертикальным линиям связи; р1 и р2 располагаются на одной вертикальной линии связи и при двухпроекционном чертеже должны быть определены двумя точками прямой р.
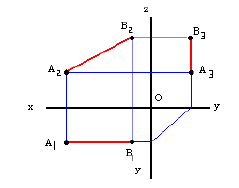
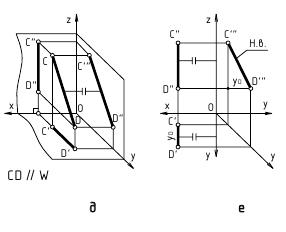
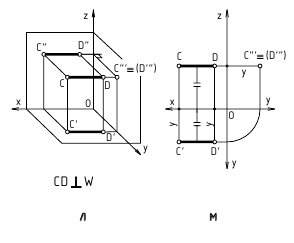
Различают горизонтально проецирующие прямые (АВ), фронтально проецирующие прямые (CD) и профильно проецирующие прямые (EF).


© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения
Научная электронная библиотека
Пиралова О. Ф., Ведякин Ф Ф.,
2.3. Положение прямой относительно плоскостей проекций. Частные положения прямой линии
Основываясь на свойствах прямой линии(3 и 4), описанных в п.2.2, следует отметить, что особый интерес в начертательной геометрии представляют прямые частного положения. К прямым частного положения относятся прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.
Линии, параллельные плоскостям проекций называются линиями уровня. Рассмотрим изображения на эпюре и отметим основные свойства этих прямых.
Прямые, параллельные плоскостям проекций.
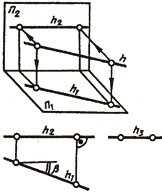
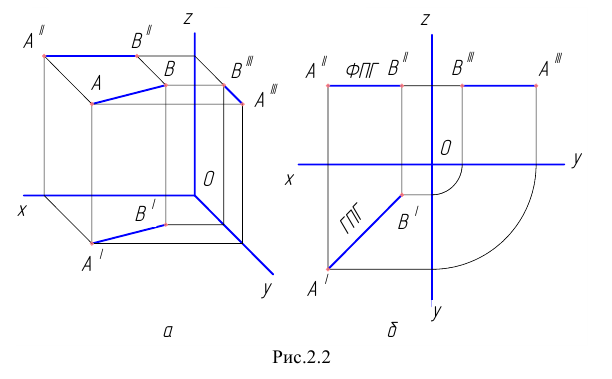
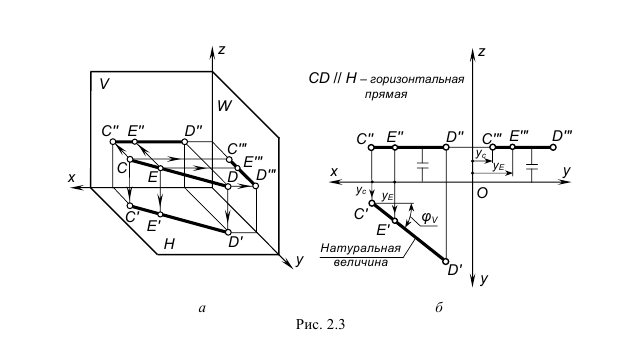
а) горизонтальная прямая h (рис. 2.2) – горизонталь.
Рис. 2.2. Горизонтальная прямая
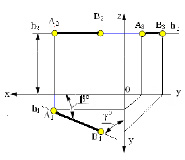
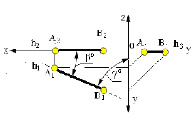
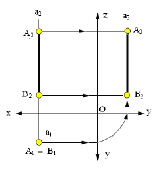
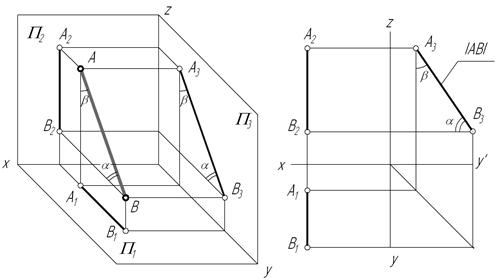
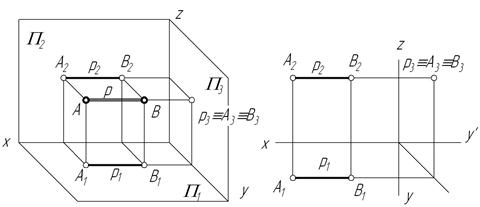
Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π1. Так как все точки этой прямой равноудалены от плоскости проекций π1 (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π1 проецируются без искажения отрезок прямой АВ (А1В1 = АВ) и углы наклона прямой к плоскостям проекций π2 и π3 (углы β0 и γ0).
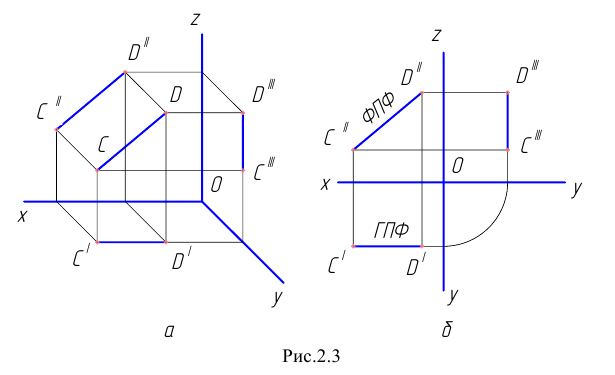
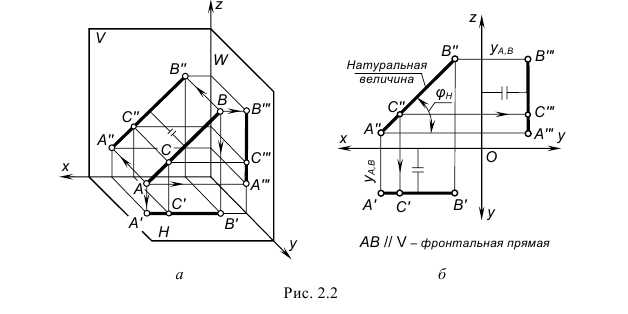
б) фронтальная прямая f (рис. 2.3) – фронталь.
Рис. 2.3. Изображение фронтальной прямой
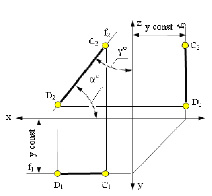
Фронтальная прямая – это прямая, параллельная фронтальной плоскости проекций π2. Так как все точки этой прямой равноудалены от плоскости проекций π2 (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π2 проецируются без искажений отрезок этой прямой CD (C2D2 = CD) и углы наклона прямой к плоскостям проекций π1 и π3 (углы α° и γ°).
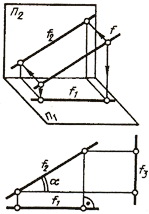
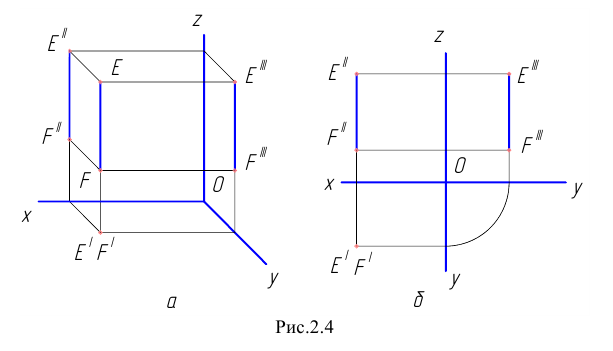
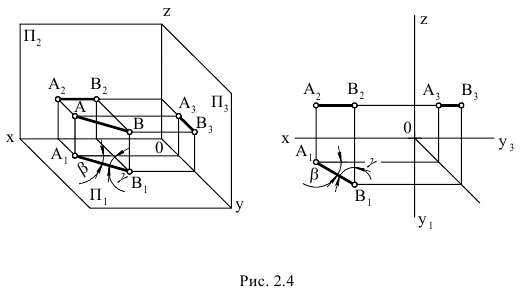
в) профильная прямая p (рис. 2.4)
Кроме прямых линий, рассмотренных выше, на комплексном чертеже, также, изображают прямые, принадлежащие плоскостям проекций. Такие прямые представляют частные случаи горизонтальных, фронтальных и профильных прямых. Характерным признаком, таких прямых на чертеже, является принадлежность одной из проекций этих прямых соответствующей оси.
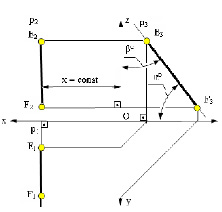
Рис. 2.4. Изображение профильной прямой
Прямые, принадлежащие плоскостям проекций
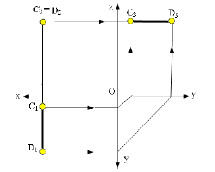
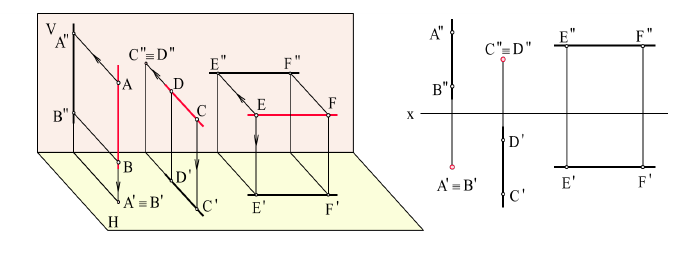
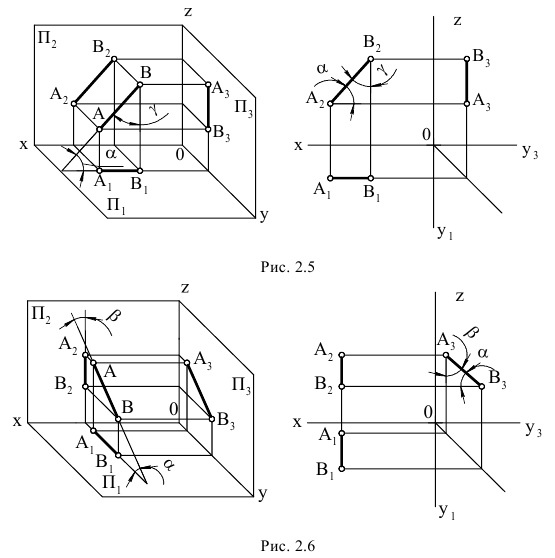
На рис. 2.5 изображена прямая АВ, которая принадлежит горизонтальной плоскости проекций АВ ⊂ π1 (частный случай горизонтальной прямой Z=0), а фронтальная проекция этой прямой А2В2 принадлежит оси х (А2В2 ⊂ X). При этом, на рисунке показаны углы наклона прямой АВ к фронтальной (β°) и профильной (γ°) плоскостям проекций.
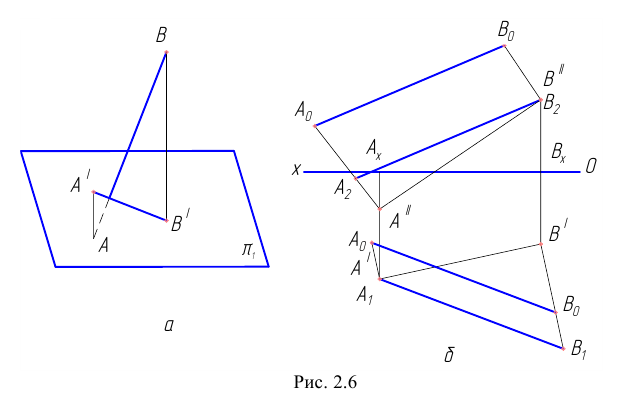
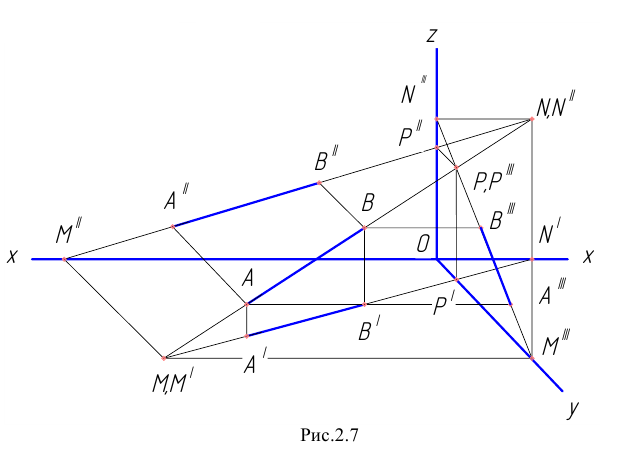
На рис. 2.6. показана прямая, принадлежащая фронтальной плоскости проекций (частный случай фронтальной прямой Y=0), а на рис. 2.7 – профильной плоскости проекций (частный случай профильной прямой Х=0) соответственно.
Рис. 2.5. Изображение прямой, принадлежащей горизонтальной плоскости проекций
Рис. 2.6. Изображение прямой, принадлежащей фронтальной плоскости проекций
Рис. 2.7. Изображение прямой, принадлежащей профильной плоскости проекций
Прямые линии, перпендикулярные плоскостям проекций.Проецирующие прямые
Прямую, параллельную направлению проецирования и перпендикулярные соответствующим плоскостям проекций называют проецирующей. При прямоугольном проецировании проецирующая прямая параллельна двум плоскостям проекций и перпендикулярна одной.
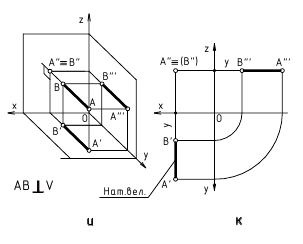
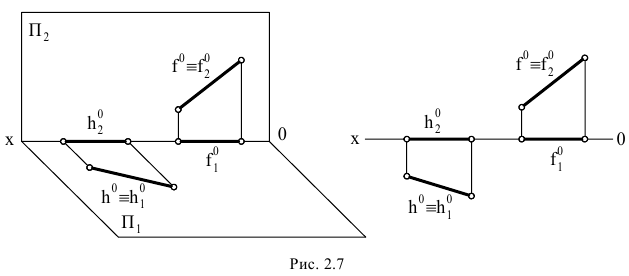
Если прямая перпендикулярна горизонтальной плоскости проекций, то она называется горизонтально-проецирующей и все её точки проецируются на эту плоскость в точку.
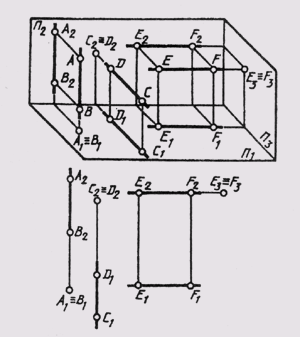
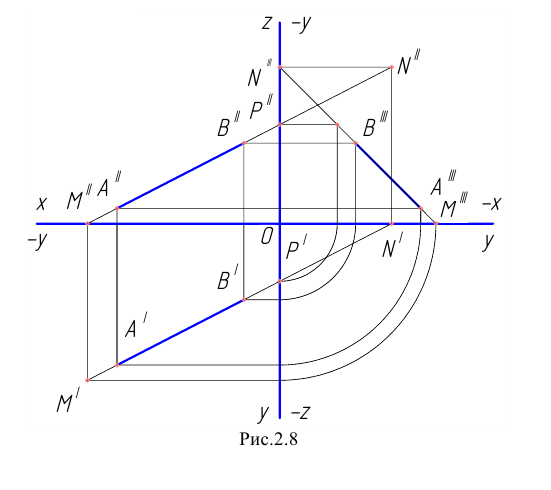
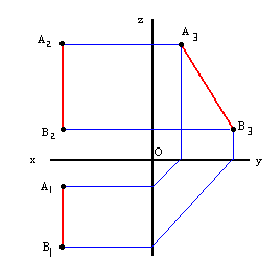
На рис. 2.8 представлена, прямая, перпендикулярная горизонтальной плоскости проекций.
В этом случае во фронтальной плоскости проекцийπ2 проекция прямой А2В2 перпендикулярна оси Х, в профильной плоскости проекций π3, А3В3 – параллельна оси Z, а в горизонтальной плоскости проекций А1 ≡ В1.
Рассматриваемая прямая расположена в первом октанте и все координаты прямой положительные
Рис. 2.8. Изображение прямой линии (горизонтально-проецирующей), перпендикулярной горизонтальной плоскости проекций
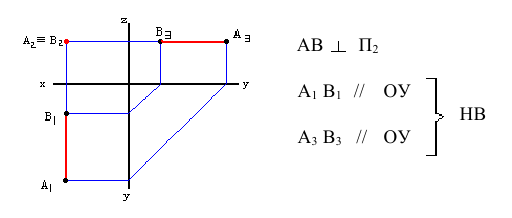
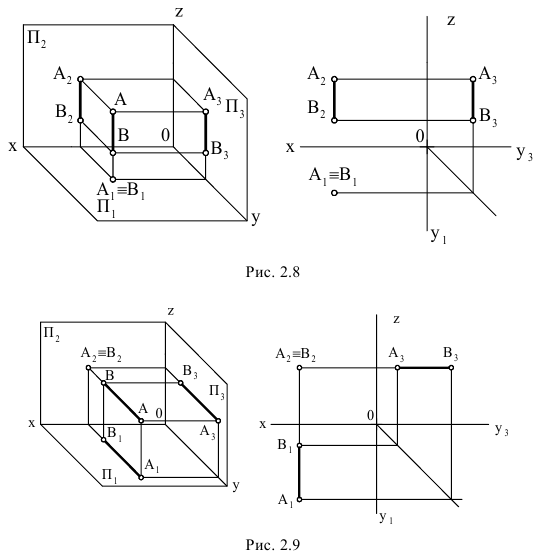
На рис. 2.9 изображена, прямая, перпендикулярная фронтальной плоскости проекций.
В этом случае в горизонтальной плоскости проекций С1D1 перпендикулярна оси Х, в профильной плоскости проекций С3D3 – параллельна оси Y, а во фронтальной плоскости проекций C2 ≡ D2.
Прямая линия, перпендикулярная фронтальной плоскости проекций называется фронтально-проецирующей прямой и она проецируется на плоскость π2 в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).
Рис. 2.9. Изображение прямой линии (фронтально-проецирующей),перпендикулярной фронтальной плоскости проекций
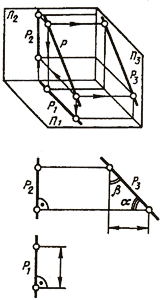
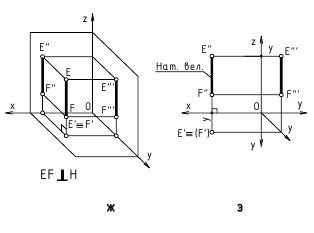
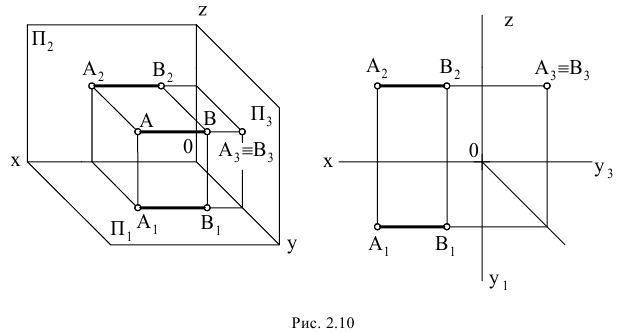
Прямая линия, перпендикулярная профильной плоскости (рис. 2.10) проекций называется профильно-проецирующей.
Рис. 2.10. Изображение прямой линии перпендикулярной профильной плоскости (профильно-проецирующей) проекций
Эта прямая проецируется на плоскость π3 в точку, а ее фронтальная проекция E2F2 перпендикулярна оси Z.
Рассмотренные прямые, являются частными случаями фронтальной и горизонтальной прямых соответственно.
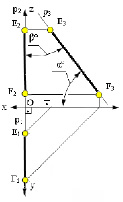
40. Расположение прямой относительно плоскостей проекций
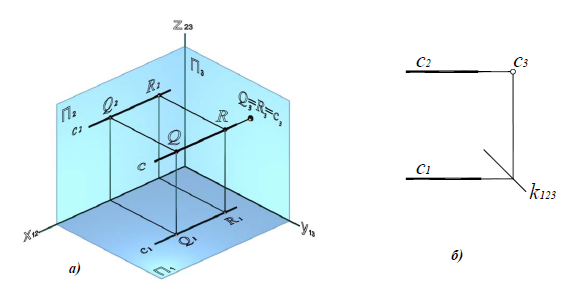
Относительно плоскостей проекций прямая может занимать различное положение. Прямую, не параллельную ни одной из основных плоскостей проекций (см. рис. 69), называют прямой общего положения. Прямую, параллельную или перпендикулярную одной из плоскостей проекций, называют прямой частного положения.
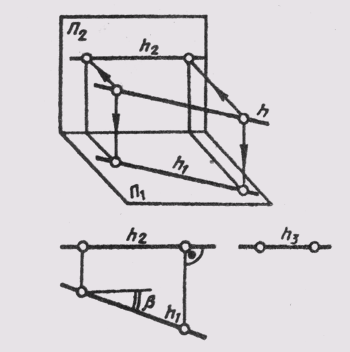
Прямые, параллельные одной из плоскостей проекций, называют прямыми уровня. Название их зависит от того, какой плоскости они параллельны. Прямую, параллельную горизонтальной плоскости проекций, называют горизонталью и обозначают на чертежах h (рис. 70).
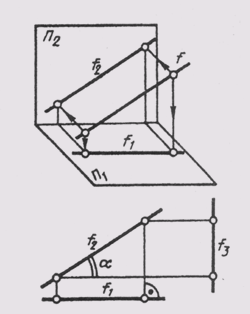
Прямую, параллельную фронтальной плоскости проекций, называют фронталью и обозначают f (рис.71).
Прямую, параллельную профильной плоскости проекций, называют профильной и обозначают р (рис. 72).
У прямой уровня одна проекция параллельна самой прямой и определяет углы наклона этой прямой к двум другим плоскостям проекций.
Параллельность одной из плоскостей проекций определяет расположение двух других проекций прямой уровня:
Прямые h2и f1 перпендикулярны вертикальным линиям связи; р1 и р2располагаются на одной вертикальной линии связи и при двухпроекционном чертеже должны быть определены двумя точками прямой р.
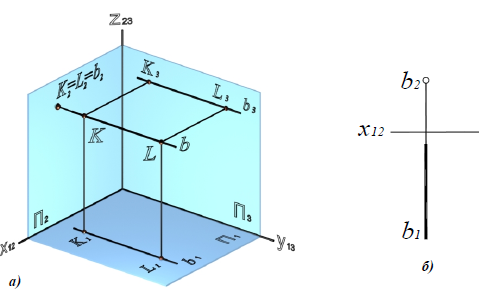
Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых одна проекция превращается в точку, а две другие проекции параллельны самой
прямой и совпадают на чертеже с направлением линии связи (рис. 73). Различают горизонтально проецирующие прямые (АВ), фронтально проецирующие прямые (CD) и профильно проецирующие прямые (EF).
Положение прямой относительно плоскостей проекций



По расположению относительно плоскостей проекций различают прямые общего и частного положения.
Прямые не параллельные и не перпендикулярные ни одной из плоскостей проекций называются прямыми общего положения.
Признаки и свойства прямой общего положения:
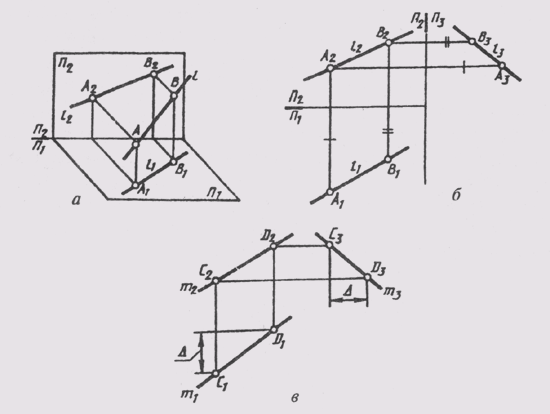
1) На КЧ ни одна из проекций прямой общего положения, не параллельна осям проекций (или не перпендикулярна линиям связи) (рис. 2.5, 2.6).
2) Длина отрезка, принадлежащего прямой общего положения проецируется на любую плоскость проекций с искажением: каждая проекция отрезка короче его натуральной величины.
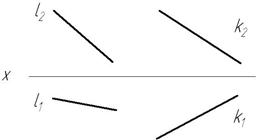
Прямые общего положения могут быть восходящими или нисходящими.
Прямая называется восходящей, если по мере удаления от наблюдателя она повышается.
Прямая называется нисходящей, если по мере удаления от наблюдателя она понижается.
Для того, чтобы определить по КЧ положение прямой, необходимо обратить внимание на то, как дальняя от наблюдателя точка отрезка прямой расположена относительно ближайшей точки: выше или ниже, правее или левее. На рисунке 2.5 изображена восходящая вправо прямая, т.к. наиболее удаленная точка В располагается правее и выше ближайшей точки А.
Признак восходящих и нисходящих прямых:
1) На КЧ горизонтальная и фронтальная проекции имеют уклон в одну сторону относительно оси проекций (рис. 2.7 – прямая l).
2) У нисходящих прямых обе проекции наклонены в разные стороны относительно оси проекций (рис. 2.7 – прямая k).
Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.
Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня.
Существует три вида прямых уровня: горизонталь, фронталь и профильная прямая.
1. Горизонталь (h)– прямая, параллельная горизонтальной плоскости проекций.
Признаки и свойства горизонтали:
1) На КЧ фронтальная проекция горизонтали 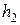
2) На горизонтальную плоскость проекций без искажения проецируются отрезок, принадлежащий горизонтали (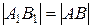
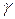
2. Фронталь (f) – прямая, параллельная фронтальной плоскости проекций.
Признаки и свойства фронтали:
1) На КЧ горизонтальная проекция фронтали 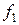
2) На фронтальную плоскость проекций проецируются без искажения отрезок, принадлежащий фронтали (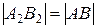
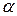
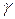
3. Профильная прямая – прямая, параллельная профильной плоскости проекций.
Признаки и свойства профильной прямой:
1) На КЧ фронтальная 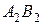
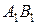
2) На профильную плоскость проекций проецируются без искажения отрезок, принадлежащий профильной прямой (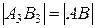
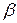
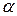
Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими прямыми.
Существует три вида проецирующих прямых: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая прямая.
Проекцией проецирующей прямой на плоскость проекций, к которой она перпендикулярна, является точка (след прямой). Все точки, принадлежащие проецирующей прямой, проецируются на ее след.
1. Горизонтально-проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций.
2. Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций.
3. Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций.
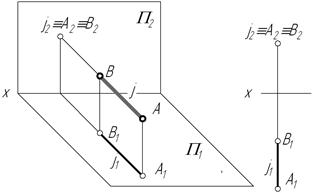
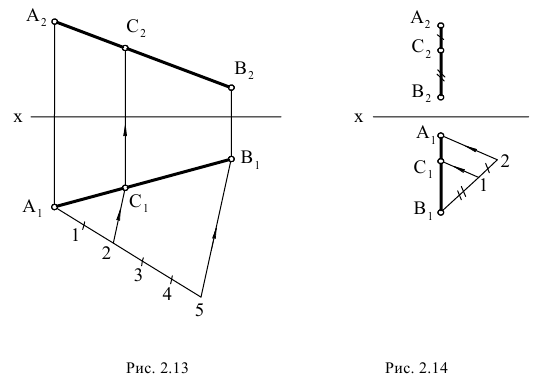
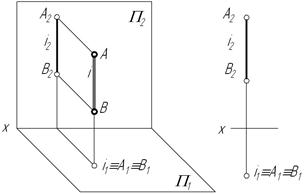
К числу частных случаев расположения прямых можно отнести и прямые, лежащие непосредственно в плоскостях проекций. Их называют прямыми нулевого уровня. На рис. 2.14 приведены примеры таких прямых: горизонталь h и профильно-проецирующая прямая j располагаются на горизонтальной плоскости проекций, следовательно их фронтальные проекции находятся на оси 0х; фронталь f и профильно-проецирующая прямая р лежат во фронтальной плоскости проекций, а значит их горизонтальные проекции на КЧ совпадают с осью 0х.
Прямая линия в начертательной геометрии с примерами
Содержание:
Общее положение прямой
Прямой общего положения называется прямая, пересекающая все плоскоcти координат.
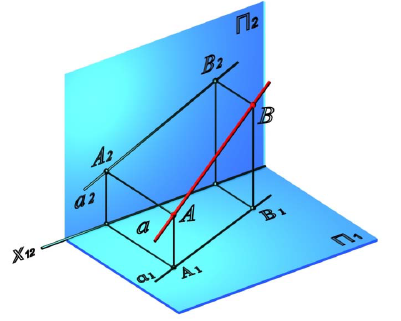
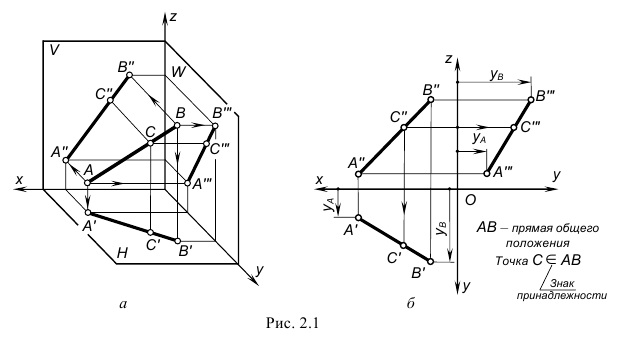
Пусть заданы две точки
Соединяя соответствующие проекции точек прямыми линиями, получим проекции прямой, заданной отрезком
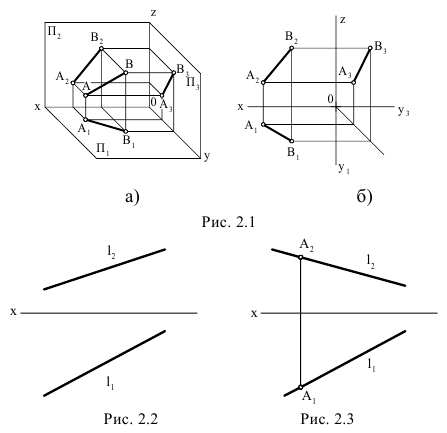
Известно, что две проекции прямой определяют её положение в пространстве. Оценив наглядность и измеримость полученного изображения, заметим:
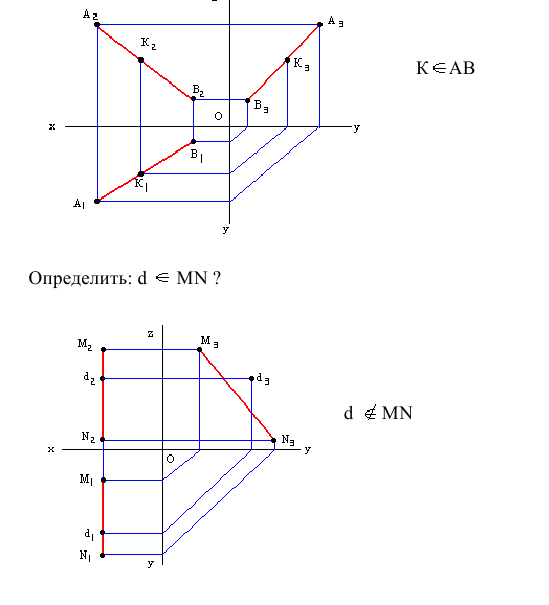
Отметим следующее важное обстоятельство: если точка лежит на прямой, то её проекции расположены на соответствующих проекциях прямой (точка С на Рис.2.1).
Известно, что две прямые, пересекаемые рядом параллельных прямых, рассекаются ими на пропорциональные части. Следовательно, отношение отрезков прямой равно отношению проекций этих отрезков, т.е.
Частные случаи положения прямой
К частным случаям положения прямой относят прямые: параллельные одной из плоскостей координат, перпендикулярные к одной из плоскостей координат, лежащие в плоскости координат, совпадающие с осью координат.
Прямым, параллельным плоскостям координат, принято давать общее название линий уровня.
Если прямая расположена в плоскости координат, то её проекция на эту плоскость совпадает с самой прямой, а две другие проекции совпадают с осями координат.
Если прямая совпадает с осью координат, то две её проекции совпадают с самой прямой, а на плоскость, перпендикулярную этой оси, прямая спроецируется точкой в начало координат.
Определение истинной длины отрезка прямой
Рассмотрим пример определения истинной длины отрезка, расположенного в первом октанте. Пусть имеются проекции 
Определим его истинную длину по фронтальной проекции. Для этого в точках 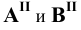
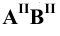
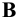
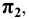
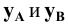
Соединяя точки 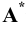
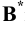

Аналогичное построение можно выполнить на горизонтальной проекции отрезка. В этом случае 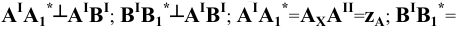
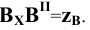
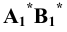
Построение можно упростить. Если отложить на перпендикуляре, восстановленном из точки 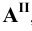
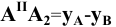
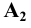
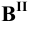
Отметим, что в способе треугольника одновременно с истинной длиной отрезка определяется угол наклона прямой к соответствующей плоскости координат:
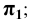
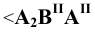
Рассмотрим пример определения истинной длины отрезка для случая, когда координаты концевых точек имеют разные знаки. Пусть, например, точка 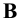
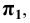
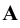
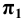
Особенностью построения в данном случае является необходимость учёта знаков недостающих координат точек, т.е. значения этих координат откладываются на перпендикулярах, восстановленных к концам проекции отрезка, в произвольные, но разные стороны (см. Рис.2.6, б). В нашем примере
При построении способом треугольника на перпендикуляре, восстановленном из точки 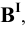
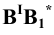
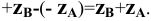
Следы прямой линии
Следом прямой линии ни данной плоскости координат называется точка пересечения (встречи) прямой с упомянутой плоскостью.
Точка пересечения прямой с плоскостью 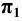
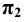
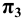
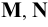
Изобразим в косоугольных проекциях (Рис.2.7) произвольный отрезок 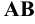
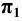
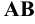
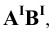
Точка 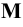
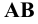
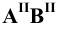
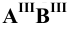
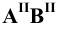
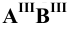
Построение проекций фронтального 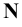
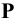
Местоположение следов прямой 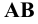
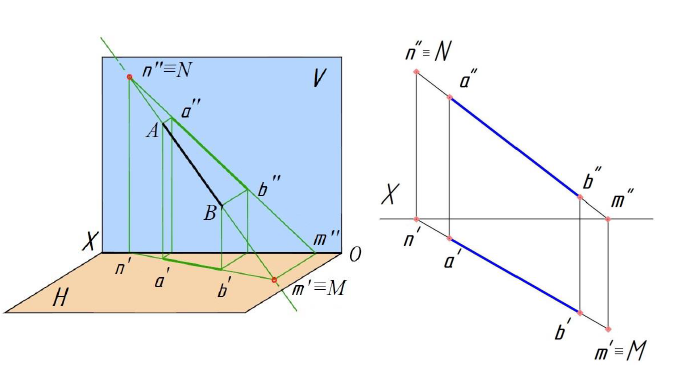
Рассмотрим построение прямоугольных проекций следов прямой общего положения, заданной проекциями отрезка 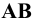
Для этого следует найти сначала фронтальную или профильную проекции этого следа. Фронтальную проекцию 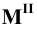
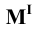
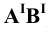
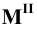
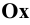
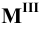
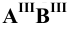
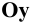
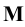
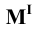
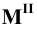
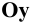
Горизонтальную проекцию 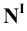
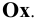
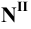
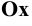
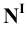
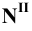
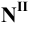
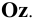
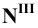
Аналогичным построением найдём проекции профильного следа.
В заключение данного раздела отметим следующее:
Взаимное положение прямых линий
Возможны три случая относительного положения прямых линий. Прямые могут быть взаимно параллельны, могут пересекаться друг с другом или скрещиваться.
Если прямые параллельны, то их соответствующие проекции тоже параллельны.
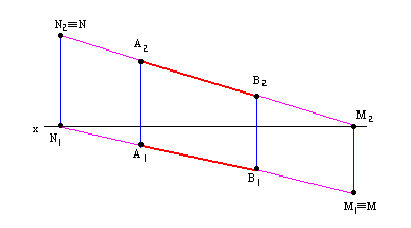
Пусть даны косоугольные проекции двух взаимно параллельных прямых 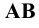
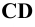
Чтобы через данную точку провести прямую, параллельную заданной, нужно через проекции этой точки провести прямые, параллельные соответствующим проекциям заданной прямой.
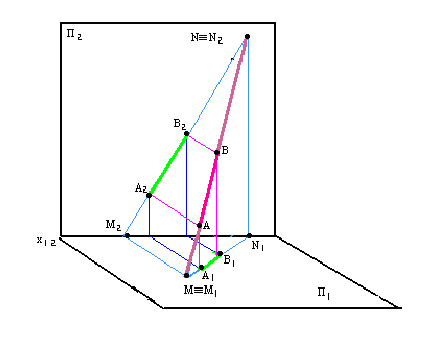
У пересекающихся прямых соответствующие проекции пересекаются и проекции точки пересечения связаны перпендикуляром к соответствующей оси координат. Пусть даны две пересекающиеся в точке 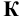
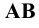
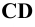
Точка 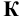

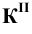
Скрещивающиеся прямые не имеют общей точки. Их проекции могут пересекаться, но точки пересечения не находятся в проекционной связи друг с другом, т. е. не лежат на перпендикуляре к соответствующей оси координат.
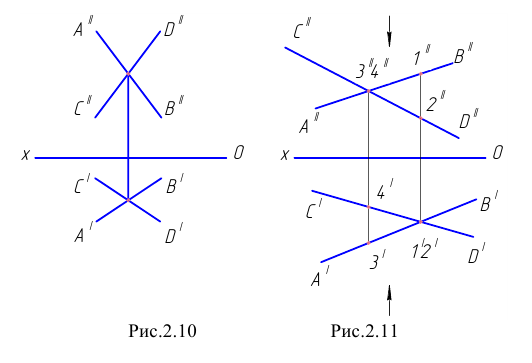
Изобразим прямоугольные проекции Рис.2.11) двух скрещивающихся прямых 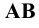
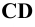
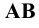
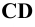
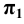
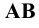
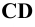
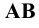
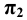
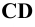
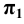
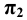
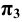
Проекции отрезка прямой линии
Как известно из элементарной геометрии, прямая линия определяется двумя точками, поэтому, чтобы построить проекции этой прямой, необходимо иметь проекции двух точек, принадлежащих этой прямой.
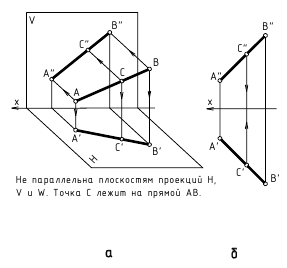
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения.
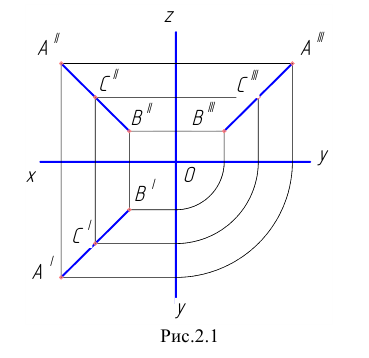
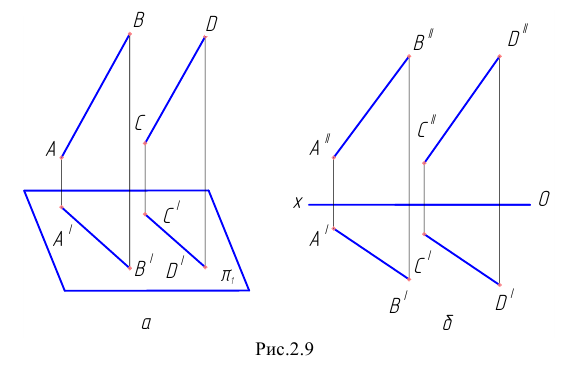
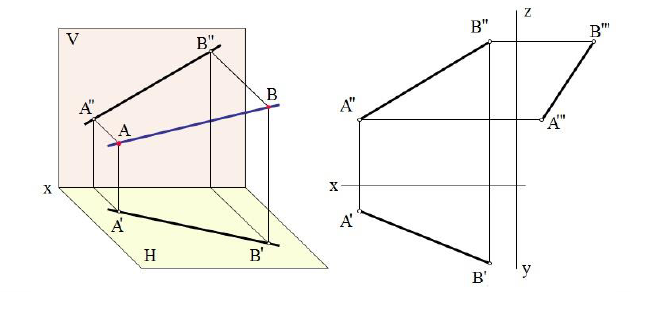
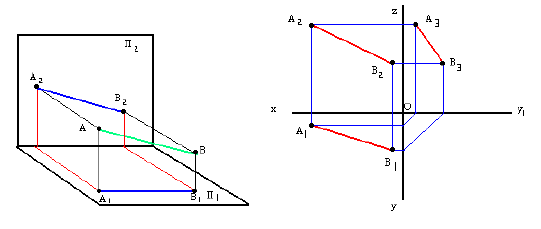
На рис. 2.1 дано пространственное изображение и чертеж прямой АВ. Точки А и В находятся на разных расстояниях от каждой из плоскостей пространства, т е. прямая АВ не параллельна не одной из них. Значит, прямая АВ общего положения.
Задание и изображение на чертеже прямой общего положения
Прямая линия в пространстве определяется положением двух ее точек, например А и В. Значит, достаточно выполнить комплексный чертеж этих точек, а затем соединить одноименные проекции точек прямыми линиями, получим соответственно горизонтальную и фронтальную проекции прямой.
Прямая общего положения называется прямая не параллельная ни одной из плоскостей проекций. Прямая, параллельная или перпендикулярная одной из плоскостей проекций, называется прямой частного положения.
Прямые, параллельные или перпендикулярные к плоскостям проекций, называются прямыми частного положения. Прямая, параллельная какой-либо одной плоскости проекций, называется прямой уровня. Существуют три линии уровня:
Прямые уровня
Прямая, параллельная одной из плоскостей проекций, называется прямой уровня.
Название зависит от того, какой плоскости она параллельна.
Различают: горизонтальную прямую уровня (горизонталь) h, фронтальную прямую уровня (фронталь) f, профильную прямую уровня (профиль) р.
Все точки прямых уровня имеют равные или высоты (горизонталь), или глубины (фронталь), или широты (профиль). Поэтому соответствующие проекции прямых параллельны проекциям определенных осей координат.
Проецирующие прямые
Прямая, перпендикулярная какой-либо плоскости проекции, называется проецирующей.
Различают: горизонтально проецирующую (АВ), фронтально проецирующую (CD) и профильно проецирующую (EF) (рис. 8).
У проецирующей прямой одна проекция вырождается в точку, а две другие проекции параллельны самой прямой и совпадают с направлением линии связи.
Следы прямой линии
Что бы найти горизонтальный след, надо продлить фронтальную проекцию а»в» (рис. 2.4) до пересечения с осью Х (точка М») и из этой точки восстановить перпендикуляр к оси X (линию связи) до пересечения с продолжением горизонтальной проекции a’b’.
Точка м’— горизонтальная проекция горизонтального следа, которая совпадает с самим следом М.
Для нахождения фронтального следа необходимо продолжить горизонтальную проекцию а’ в’ до пересечения с осью X (точка n’) и через точку n’, которая является горизонтальной проекцией фронтального следа, провести перпендикуляр к оси X до пересечения с продолжением фронтальной проекцией а»в». Точка n»— фронтальная проекция фронтального следа, которая совпадает с фронтальным следом N.
Отметим, что прямая не имеет следа на плоскости проекций в том случае, если она параллельна этой плоскости.
Определение натуральной величины отрезка и углов его наклона к плоскостям проекций
Возьмем отрезок АВ (рис. 2.5) и построим его ортогональную проекцию на горизонтальной плоскости проекций Н. В пространстве при этом образуется прямоугольный треугольник A’BB’, в котором одним катетом является горизонтальная проекция этого отрезка, вторым катетом разность высот точек А и В отрезка, а гипотенузой является сам отрезок.
На чертеже прямоугольный треугольник построен на горизонтальной проекции отрезка АВ, второй катет треугольника 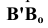
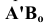
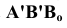
Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов, замеренную на плоскости Н.
Деление отрезка прямой линии
Иногда требуется разделить отрезок в данном отношении. Из свойств параллельного проецирования известно, что отношение отрезков одной и той же прямой равно отношению проекций эти отрезков.
Чтобы разделить отрезок прямой в заданном отношении, необходимо разделить в этом отношении одну из проекций этого отрезка, а затем с помощью линий связи перенести делящую точку на другие проекции.
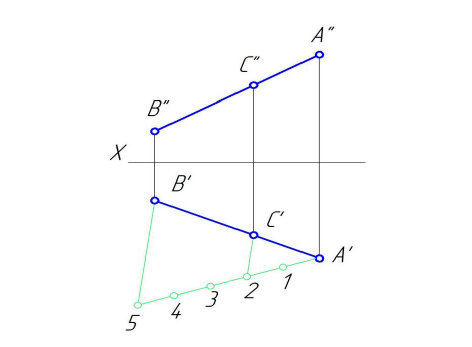
На рис. 2.6 дан пример деления отрезка прямой линии АВ в отношение 2 : 3.
Из точки А’ проведен вспомогательный отрезок прямой, на котором отложено пять одинаковых частей произвольной длинны. Проведя отрезок В’5 и параллельно ему точку 2 прямую, получим точку С’ причем А’К’ : КБ’ = 2 : 3; затем линии связи находим точку С». Точка С делит отрезок АВ в отношении 2 : 3.
Взаимное расположение двух прямых
Правило определения видимости на комплексном чертеже:
из двух горизонтально конкурирующих точек на поле Н видна та точка, которая расположена выше, а из двух фронтально конкурирующих точек на поле V видна та точка, которая расположена ближе (по отношению к наблюдателю).
Взаимное расположение точки и прямой
Из свойств параллельного проецирования (свойство принадлежности) известно, что если точка лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой.
Поэтому, из четырех точек А, В, С и D, приведенных на чертеже (рис. 2.8), лишь одна точка А лежит на прямой. Точка В находится над прямой, так как она расположена выше, чем горизонтально конкурирующая с ней точка прямой а (фронтальная проекция этой точки прямой а отмечена крестиком). Аналогично, точка С находится перед прямой а, точка D расположена ниже и дальше точки прямой а.
Определение взаимного положения точки и профильной прямой выполняется с помощью построения профильной проекции. На рис. 2.8 точка С расположена над и перед прямой АВ.
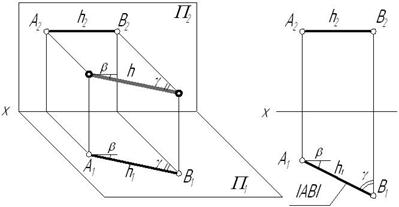
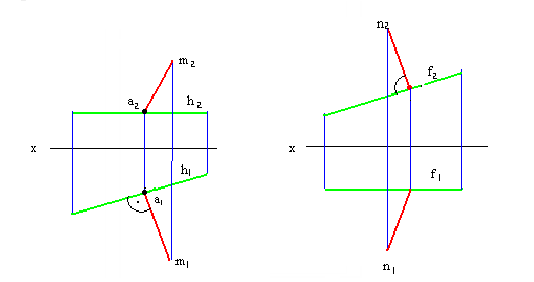
Взаимно перпендикулярные прямые
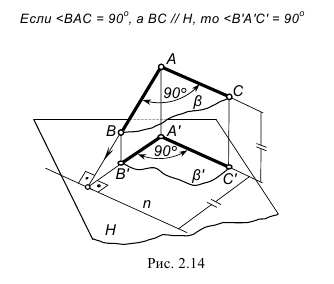
Для того, чтобы прямой угол проецировался без искажения, необходимо и достаточно, чтобы одна его сторона была параллельна, а другая не перпендикулярна к плоскости проекций.
Пусть сторона АВ прямого угла ABC параллельна плоскости Н. Требуется доказать, что проекция его: угол А’В’С’ равен 90.
Прямая АВ перпендикулярна плоскости, так как АВ перпендикулярна двум прямым этой плоскости ВС и ВВ’, проходящих через точку В. Прямая АВ и ее прекция А’В’ две параллельные прямые, поэтому А’В’ также перпендикулярна плоскости. Следовательно, А’В’ перпендикулярна В’С’.
Две взаимно перпендикулярные прямые (рис. 2.9) (пересекающиеся или скрещивающиеся) тогда сохраняют свою перпендикулярность в горизонтальной проекции, если одна из этих прямых является горизонталью.
Две взаимно перпендикулярные прямые сохраняют свою перпендикулярность во фронтальной проекции, если одна из них является фронталыю.
Проецирование отрезка прямой
Для этого необходимо и достаточно спроецировать две конечные точки отрезка.
Положение прямой относительно плоскостей проекций
Прямые уровня
Это прямые, параллельные одной из плоскостей проекций, на которую они проецируются в натуральную величину. Они находятся на одном уровне от соответствующей плоскости.
Профильная и фронтальные проекции // со ответственно осям X и У
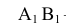
Проецирующие прямые
Это прямые, перпендикулярные одной из плоскостей проекций, на которую они проецируются в точку. Они совпадают с направлением проецирования.
Проецирующие прямые одновременно параллельны двум другим плоскостям проекций.
Точка на прямой
Если точка принадлежит прямой, то её проекции лежат на одноименных проекциях этой прямой.
Следы прямой
Точка пересечения прямой с плоскостями называется следом прямой.
Чтобы построить горизонтальный след прямой необходимо:
Для построения фронтального следа надо продолжить горизонтальную проекцию 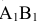
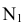
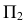
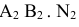
Дан отрезок общего положения. Найти горизонтальный и фронтальный следы.
Взаимное положение прямых
2. Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а точка их пересечения лежит на одной линии связи.
Справедливо и обратное, кроме профильных прямых.
3. Если прямые не параллельны и не пересекаются, то они называются скрещивающимися.
Проецирование прямого угла
Прямой угол проецируется прямым, если одна из его сторон параллельна одной из плоскостей проекций, т.е. является фронтальной или горизонтальной прямой. (Прямой угол проецируется прямым па ту плоскость проекции, кото рои параллельна одна из его сторон, т. е. является фронтальной или горизонтальной прямой).
Определение натуральной величины отрезка прямой общего положения способом прямоугольного треугольника
Угол между прямой линией и плоскостью проекций определяется как угол между прямой и её проекцией на эту плоскость.
Что такое прямая линия
Способы задания прямой
Классификация прямых
В зависимости от положения прямых относительно плоскостей проекций различают прямые общего положения и прямые частного положения.
Прямые общего положения
Прямые частного положения
Среди прямых частного положения различают линии уровня и проецирующие прямые.
Линии уровня
Прямые линии, параллельные какой-либо плоскости проекций, называются линиями уровня.
Рис. 4.3. Горизонталь:
a – наглядное изображение; б – комплексный чертеж
Поскольку высоты всех точек горизонтали равны между собой: h2
Любой отрезок горизонтали проецируется на П1 в натуральную величину:
[A1B1 ] = [AB ].
Угол наклона h к Π2 также проецируется на П1 в натуральную величину:
Фронталь 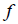
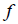
Поскольку глубина всех точек фронтали одинакова: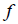
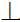
Отрезки фронтали и угол наклона к П1 проецируются на П1 в натуральную величину:[C2D2] =[CD]; Zβ1=Zβ=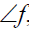
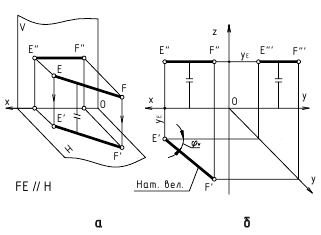
Поскольку широта всех точек профильной прямой одинакова: р2 
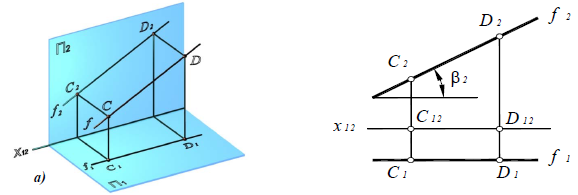
Отрезки профильной прямой и углы наклона к П1 и П2 проецируются на П3 в натуральную величину: [E3F3] =[EF];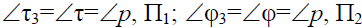
Проецирующие прямые
Прямая линия, перпендикулярная одной из плоскостей проекций или параллельная направлению проецирования, называется проецирующей.
Взаимное положение прямых линий
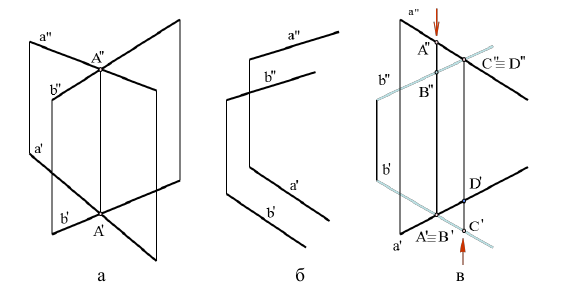
Прямые линии в пространстве могут быть параллельными, пересекающимися или скрещивающимися.
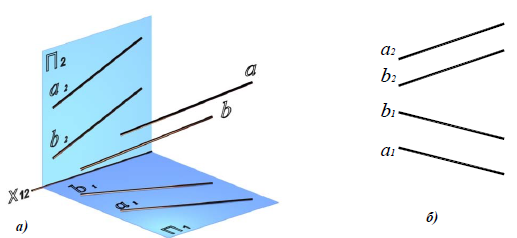
Если прямые параллельны (рис. 4.9), то их одноименные проекции параллельны: a || b 
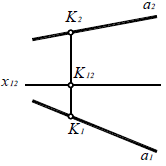
Пересекающиеся прямые имеют общую точку (рис. 4.10), то есть точки пересечения их одноименных проекций лежат на общей линии связи:
c × d = K 
c 2 × d2 = K2 и K 1 K 2 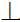
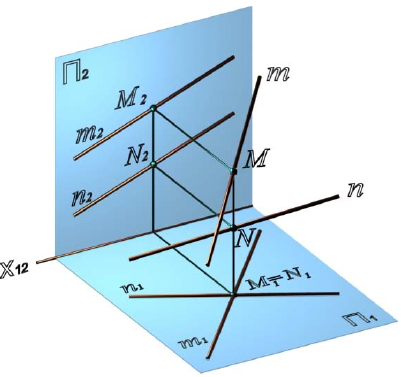
Прямые, не имеющие общей точки и не параллельные между собой, являются скрещивающимися (рис. 4.11, 4.12).
Рис. 4.11. Скрещивающиеся прямые m и n
Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях.
Принадлежность точки прямой линии
Точка принадлежит прямой, если ее проекции принадлежат соответствующим (одноименным) проекциям прямой (рис. 4.13).
Рис. 4.13. Принадлежность точки прямой линии:
K ∈ a 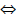
[K1K2 ]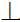
Определение натуральной величины отрезка. Способ треугольника
Рис. 4.14. Определение натуральной величины отрезка способом треугольника
Таким образом, можно сформулировать общее правило:
Проекции прямой. Положение прямой относительно плоскостей проекций
Относительно плоскостей проекций H, V и W прямые линии могут занимать различные положения и имеют соответствующие наименования, а на чертежах проекции этих прямых занимают относительно осей проекций x, y и z характерные положения. Следовательно, по чертежу прямой линии можно мысленно представить ее пространственное положение относительно плоскостей проекций, т. е. научиться «читать» чертеж прямой.
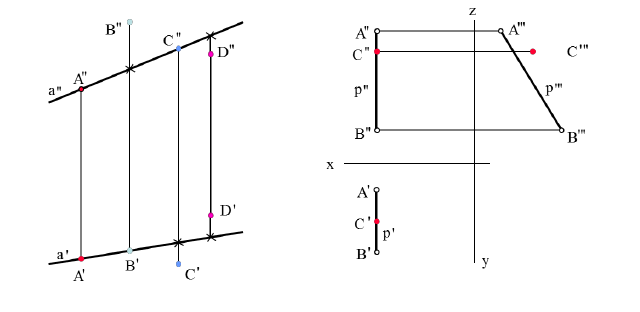
Прямые общего положения – не параллельны (и соответственно не перпендикулярны) плоскостям проекций H, V и W. Следовательно, на чертеже проекции прямых общего положения не параллельны (и не перпендикулярны) осям проекций x, y и z. Отсюда проекции прямых общего положения искажают их натуральную величину.
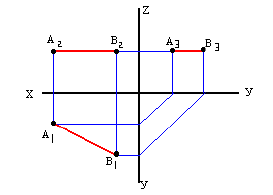
На рис. 2.1 изображены проекции прямой общего положения АВ, фронтальная A»B» и горизонтальная A’B’ проекции которой расположены произвольно относительно оси проекций x, но не параллельны и не перпендикулярны оси x – это характерный признак прямой общего положения на чертеже! Профильная проекция A»‘B»‘ прямой общего положения также должна быть не параллельна и не перпендикулярна осям проекций z и y, что и показывает построение.
Точка на прямой. Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже одноименные проекции точки лежат на одноименных проекциях прямой.
На рис. 1.4 показано построение проекций точки С, принадлежащей прямой АВ.
Прямые особого (частного) положения
Прямые уровня – прямые, параллельные одной плоскости проекций:
На рис. 2.2 изображены проекции фронтальной прямой АВ и принадлежащей ей точки С. Запомните характерные признаки расположения проекций фронтальной прямой на чертеже:
На рис. 2.3 изображены проекции горизонтальной прямой CD и принадлежащей ей точки Е. Запомните характерные признаки расположения проекций горизонтальной прямой на чертеже:
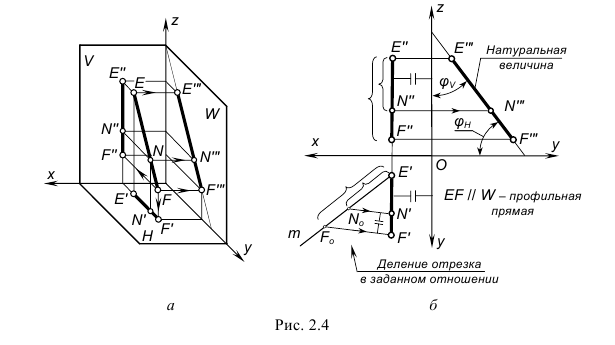
На рис. 2.4 изображены проекции профильной прямой EF и принадлежащей ей точки N. Запомните характерные признаки расположения проекций профильной прямой на чертеже:
Деление отрезка в заданном отношении
На рис. 2.4 показано построение горизонтальной проекции N’ точки N, принадлежащей профильной прямой EF. Построение основано на одном из свойств параллельного проецирования: отношение отрезков прямой линии равно отношению их проекций.
Пусть точка N делит отрезок EF в каком-то отношении. Следовательно, проекции отрезка делятся в том же отношении. Если, например, дана фронтальная проекция N» точки N, принадлежащей отрезку EF, то для построения горизонтальной проекции N’ на горизонтальной проекции E’F’ отрезка нужно выполнить следующие графические действия:
Прямые проецирующие – перпендикулярные одной плоскости проекций (параллельные двум плоскостям проекций):
. Поскольку положение проецирующих прямых совпадает по направлению с проецирующим лучом к одной из плоскостей проекций, то одна из проекций прямых проецируется (вырождается) в точку. Говорят, что проецирующие прямые обладают «собирательным» свойством, так как их вырожденные проекции-точки «собирают», то есть представляют собой проекции всех точек, лежащих на этих прямых.
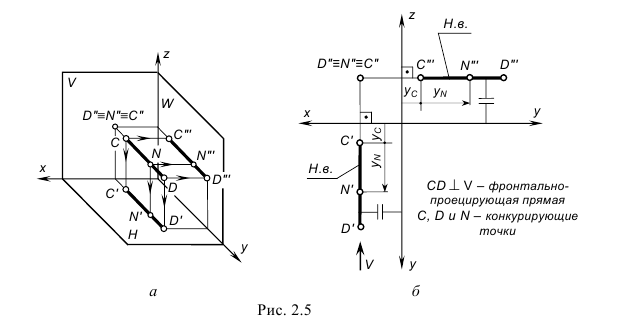
На рис. 2.5 изображены проекции фронтально-проецирующей прямой CD и принадлежащей ей точки N. Запомните характерные признаки расположения проекций фронтально-проецирующей прямой на чертеже:
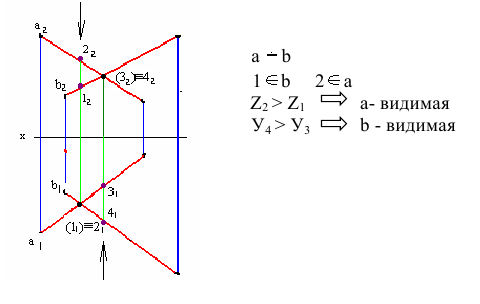
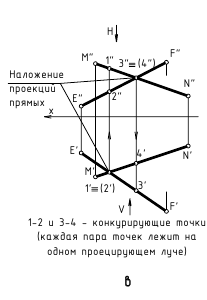
. Конкурирующие точки – точки, лежащие на одном проецирующем луче, называются конкурирующими.
На рис. 2.5 точки C, D и N на прямой CD являются конкурирующими и по их расположению на прямой относительно плоскости V (по координатам y) можно определить на горизонтальной проекции порядок их «видимости»: ближе к наблюдателю и дальше от плоскости V (с наибольшей координатой y) находится точка D, затем точка N и точка C.
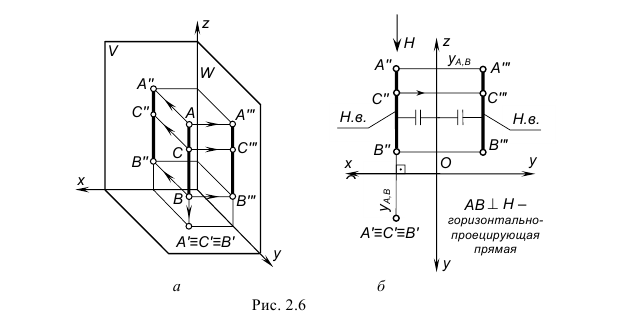
На рис. 2.6 изображены проекции горизонтально-проецирующей прямой AB и принадлежащей ей точки C. Запомните характерные признаки расположения проекций горизонтально-проецирующей прямой на чертеже:
– горизонтальная проекция AB(A’B’) представляет собой точку, т. е. горизонтальные проекции точек A, B и C совпадают как лежащие на одном проецирующем луче к плоскости проекций H;
– фронтальная проекция A»B» расположена перпендикулярно оси x и определяет натуральную величину прямой;
– профильная проекция A»‘B»‘ по построению располагается параллельно оси z и также определяет натуральную величину прямой.
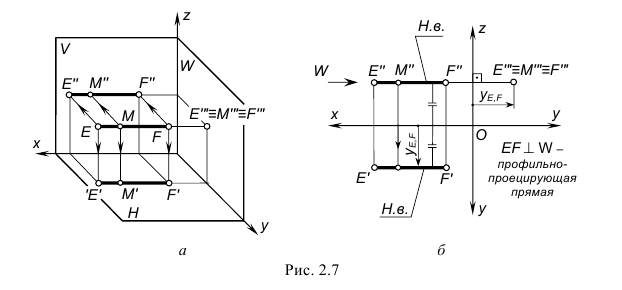
На рис. 2.7 изображены проекции профильно-проецирующей прямой EF и принадлежащей ей точки M. Запомните характерные признаки расположения проекций профильно-проецирующей прямой на чертеже:
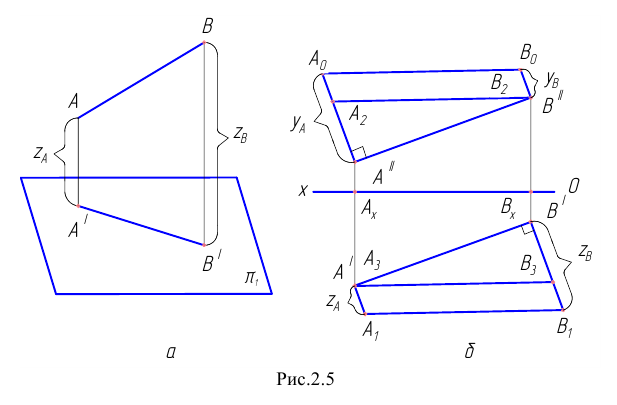
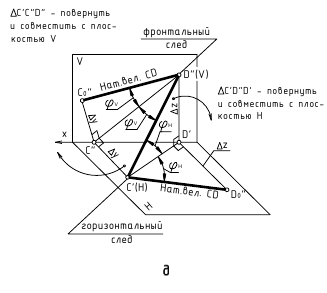
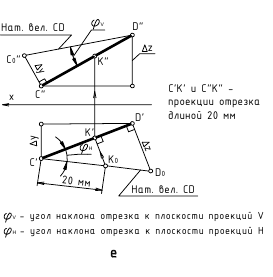
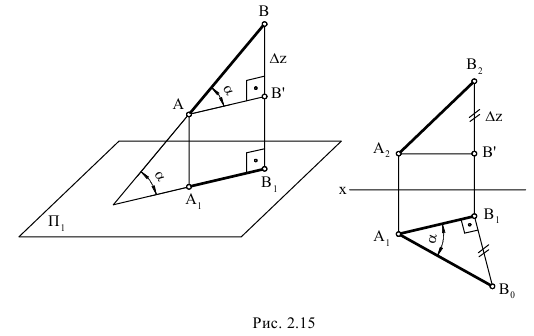
Определение по чертежу натуральной величины отрезка прямой общего положения способом прямоугольного треугольника и углов ее наклона к плоскостям проекций H и V.
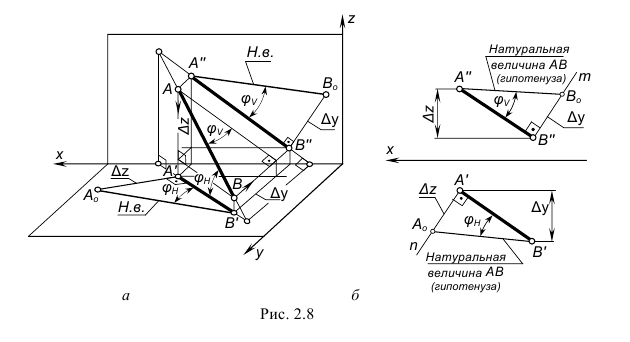
Натуральной величиной заданного на чертеже отрезка прямой общего положения является гипотенуза построенного прямоугольного треугольника, одним катетом которого может быть горизонтальная (или фронтальная) проекция отрезка, а вторым катетом этого треугольника будет разница координат ∆z (или ∆y) конечных точек этого отрезка относительно оси проекций x.
На рис. 2.8 показано построение натуральной величины заданного отрезка AB способом прямоугольного треугольника относительно фронтальной и горизонтальной его проекций, для чего выполнен следующий графический алгоритм (графические действия):
Аналогичные построения выполнены относительно горизонтальной проекции отрезка A’B’ – гипотенуза А’Bо также определяет натуральную величину заданного отрезка.
В построенных прямоугольных треугольниках углы между проекциями отрезка и гипотенузой определяют углы наклона прямой к плоскостям проекций H и V:
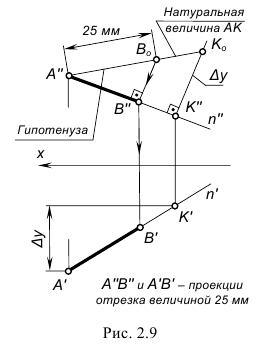
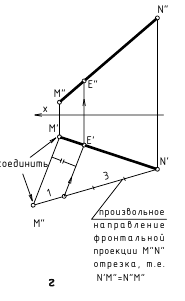
. В задачах по начертательной геометрии часто требуется построить на прямой общего положения, не имеющей второй конечной точки, проекции отрезка какой-либо заданной величины.
На рис. 2.9 показано построение на прямой n с одной конечной точкой A проекций отрезка AB заданной величины 25 мм, для чего выполнен следующий графический алгоритм (графические действия):
Понятие о следах прямой
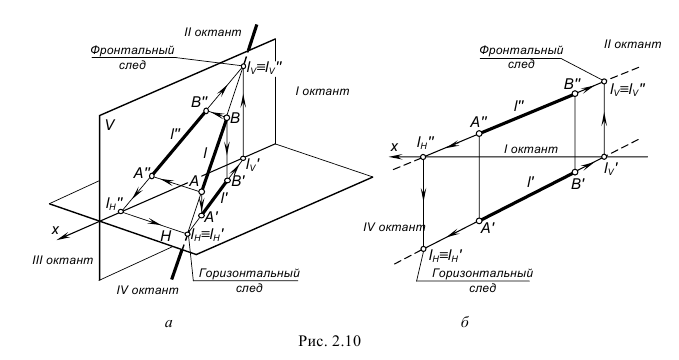
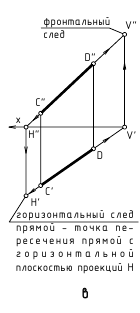
Следами прямой называются точки ее пересечения с плоскостями проекций.
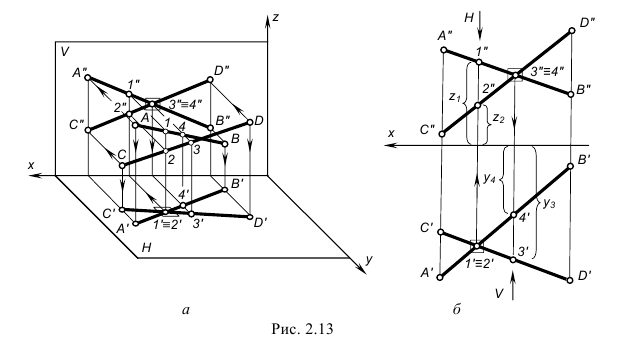
На рис. 2.10 показано построение на чертеже фронтального и горизонтального следов прямой АВ и определено прохождение прямой по октантам пространства: из IV через I во II.
Взаимное положение двух прямых
Две прямые в пространстве могут быть параллельными, пересекаться или скрещиваться. Запомните характерные признаки расположения на чертеже проекций двух различно расположенных прямых.
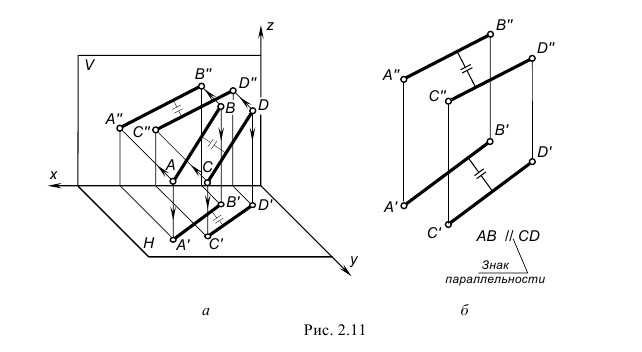
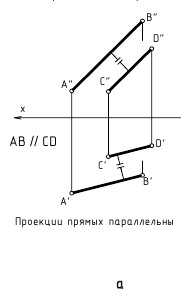
Параллельные прямые. Если прямые в пространстве параллельны, то их одноименные проекции на чертеже также параллельны.
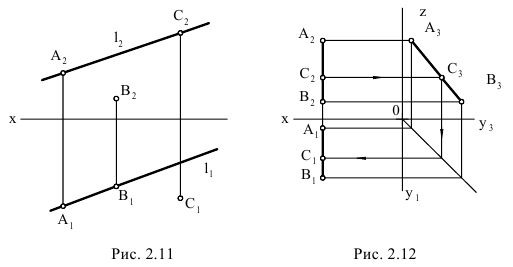
На рис. 2.11 изображены параллельные прямые AB и CD. На чертеже фронтальные и горизонтальные проекции прямых параллельны: A»B»//C»D» и A’B’//C’D’.
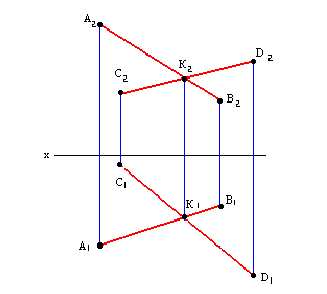
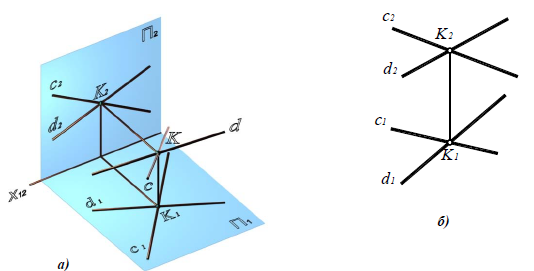
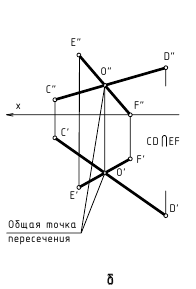
Пересекающиеся прямые. Если прямые в пространстве пересекаются, то на чертеже проекции точки пересечения прямых лежат на одной линии связи.
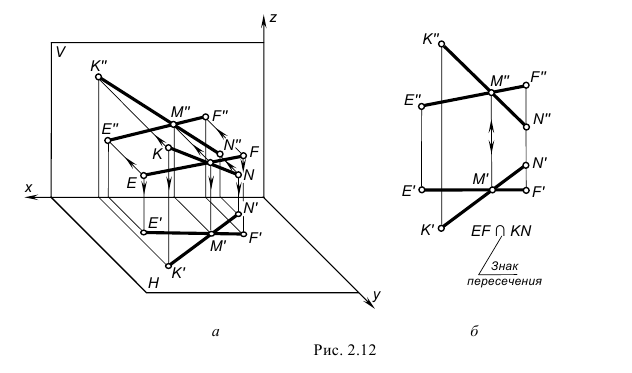
На рис. 2.12 изображены проекции пересекающихся прямых EF и KN. Проекции точки их пересечения M(M»,M’) лежат на пересечении одноименных проекций прямых и на одной линии связи.
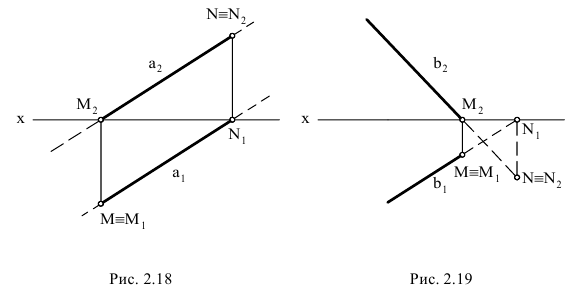
Скрещивающиеся прямые
Если две прямые не параллельны и не пересекаются, то они в пространстве скрещиваются. На чертеже их проекции могут накладываться, образуя конкурирующие точки, лежащие на одном проецирующем луче.
На рис. 2.13 изображены проекции двух скрещивающихся прямых АВ и CD. Их одноименные проекции накладываются и образуют четыре конкурирующие точки (2 пары):
. Конкурирующие точки, как было сказано выше, позволяют наблюдателю определить по чертежу относительное расположение прямых по их удаленности от плоскостей проекций H и V:
Теорема о проекции прямого угла. Частное положение прямых – перпендикулярные прямые
Пересекающиеся прямые в пространстве могут быть расположены под прямым углом, т. е. взаимно перпендикулярно. Прямой угол между перпендикулярными прямыми может проецироваться на чертеж в натуральную величину при определенном условии.
Теорема о проекции прямого угла:
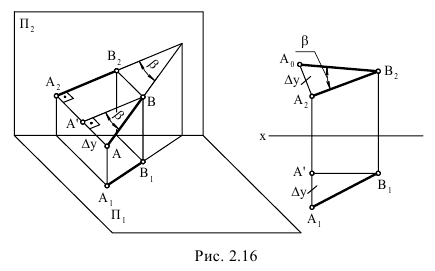
На рис. 2.14 дано изображение, поясняющее теорему о проекции прямого угла. Две перпендикулярные прямые AB и AC, образующие плоскость β, проецируются на некоторую плоскость проекций H. Прямая AС по условию параллельна этой плоскости проекций. Доказательство теоремы основано на известной из геометрии теореме о трех перпендикулярах (обратная теорема): прямая n, проведенная в плоскости H перпендикулярно наклонной прямой АВ (n
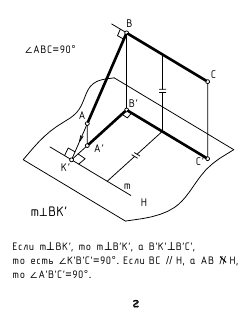
. Для решения многих задач начертательной геометрии требуется по условию строить проекции прямого угла.
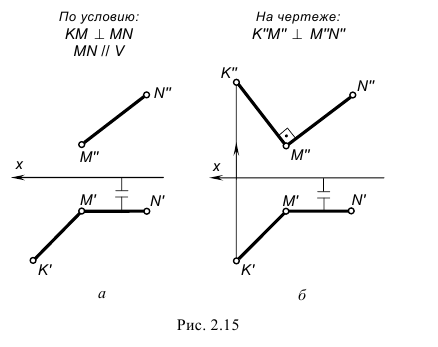
На рис. 2.15, а, б показано построение на чертеже недостающей фронтальной проекции прямого угла KMN.
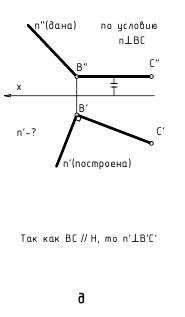
На рис. 2.15, а изображено графическое условие задачи: дана горизонтальная проекция K’M’N’ прямого угла и фронтальная проекции M»N» одной стороны этого угла.
На рис. 2.15, б показано решение задачи: так как одна сторона MN прямого угла по условию является фронтальной прямой, т. е. параллельна фронтальной плоскости проекций V, то по теореме о проекции прямого угла на плоскость V заданный прямой угол KMN должен проецироваться прямым; следовательно, фронтальную проекцию K»M» стороны KM прямого угла проводим перпендикулярно заданной фронтальной проекции стороны MN(M»N»).
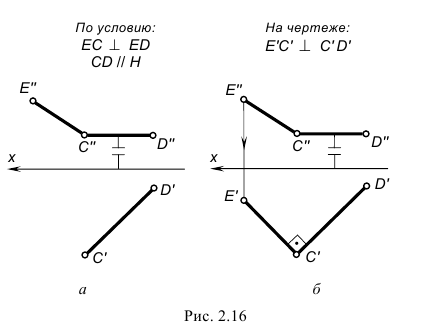
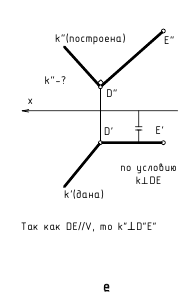
На рис. 2.16, а, б показано построение на чертеже недостающей горизонтальной проекции прямого угла ECD.
На рис. 2.16, а изображено графическое условие задачи: дана фронтальная проекция E»C»D» прямого угла и горизонтальная проекция C’D’ одной стороны этого угла.
На рис. 2.16, б показано решение задачи: так как одна сторона CD прямого угла по условию является горизонтальной прямой, т. е. параллельна горизонтальной плоскости проекций H, то по теореме о проекции прямого угла на плоскость H заданный прямой угол ECD должен проецироваться прямым; следовательно, горизонтальную проекцию E’C’ стороны угла EC проводим перпендикулярно заданной горизонтальной проекции стороны CD(C’D’).
Структуризация материала второй лекции в рассмотренном объеме схематически представлена на рис. 2.17 (лист 1). На последующих листах 2–4 компактно приведены иллюстрации к этой схеме, способствующие закреплению изученного материала и его быстрому визуальному повторению (рис. 2.18–2.20).
Проекции прямой. Положение прямой относительно плоскостей проекций. Взаимное положение прямых. Способ прямоугольного треугольника. Теорема о проекции прямого угла
Прямые обозначают на чертеже строчными буквами латинского алфавита: а, в, m, n и т.д. Отрезки прямых обозначаются прописными буквами: АВ, MN и т.д.
Прямая общего положения
Прямая общего положения и её проекции
Деление отрезка в заданном отношении (например, 1:3)
Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже одноимённые проекции точки лежат на одноимённых проекциях прямой (см. рис. 2.1а, б; 2.4б).
Определение натуральной величины отрезка способом прямоугольного треугольника на чертеже
Прямые частного положения
Горизонтальная прямая уровня: //H
Фронтальная прямая уровня: //V
Профильная прямая уровня: //W
Горизонтально-проецирующая прямая: 
Фронтально-проецирующая прямая: 
Профильно-проецирующая прямая: 
Взаимное расположение прямых
Теорема о проекции прямого угла
Теорема о проекции прямого угла: если одна сторона прямого угла пареллельна плоскости проекций (а вторая не параллельна и не перпендикулярна этой плоскости), то на эту плоскость проекций прямой угол проецируется в виде прямого угла.
Знак перпендикулярности элементов:
Задание прямой
Положение прямой линии в пространстве определяется двумя точками или точкой и направлением. Поэтому на эпюре прямую можно задать проекциями ее отрезка (рис. 2.1), проекциями некоторой произвольной части прямой, не указывая концевых точек этой части (рис. 2.2), или указывая одну точку этой прямой (рис. 2.3).
Прямая общего положения
Прямая общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
На эпюре проекции прямой общего положения составляют с осями проекций произвольные углы, поэтому величина каждой проекции меньше истинной величины самой прямой (см. рис. 2.1).
Прямые частного положения
Прямые, параллельные или перпендикулярные плоскостям проекций, называют прямыми частного положения.
Прямая, параллельная какой-либо плоскости проекций, а с двумя другими плоскостями образующая произвольные углы, называется прямой уровня. Различают три линии уровня:
На рис. 2.4 видно, что все точки горизонтальной прямой 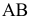
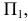
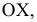
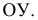
Эти отличительные особенности характерны и для фронтальной и профильной прямых.
Прямые уровня могут принадлежать плоскостям проекций. Такие прямые называют нулевой горизонталью и нулевой фронталью (рис. 2.7).
Прямые, перпендикулярные одной из плоскостей проекций, а двум другим параллельные, называются проецирующими:
Принадлежность точки прямой. Деление отрезка прямой линии в данном отношении
Если точка лежит на прямой, то ее проекции будут лежать на одноименных проекциях этой прямой.
На рис. 2.11 изображена прямая и три точки: 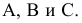
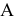
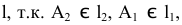
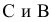
На рис. 2.12 показано построение точки 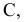
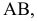
Чтобы разделить отрезок прямой в данном отношении, достаточно разделить в этом отношении одну из проекции заданного отрезка, а потом с помощью линии связи перенести делящую точку на другие проекции отрезка.
На рис. 2.13 точка 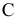
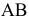
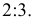
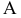
Если необходимо разделить отрезок профильной прямой 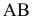
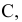
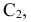
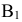
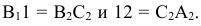
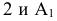
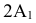
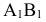
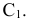
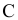
Определение длины отрезка прямой общего положения и углов наклона прямой к плоскостям проекций
Для определения натуральной величины отрезка прямой общего положения необходимо построить на чертеже прямоугольный треугольник, одним катетом которого является проекция отрезка на какую-либо плоскость проекций, а величина другого катета равна разности расстояний концов отрезка от плоскости проекций, на которой взяли первый катет. Натуральная величина отрезка прямой будет равна гипотенузе этого треугольника. Угол между катетом-проекцией и гипотенузой равен углу наклона отрезка к этой плоскости проекций.
На рис. 2.15 показано проецирование отрезка 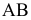
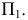
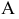
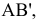
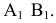
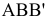
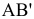
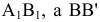
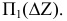
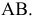
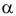
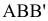
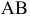
Для определения угла наклона отрезка прямой 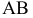
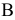
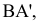
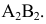
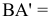
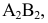
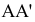
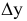
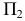
Угол 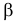
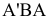
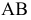
Следы прямой линии
Для построения горизонтального следа 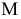
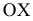
Для построения фронтального следа прямой продолжаем горизонтальную проекцию прямой до пересечения с осью 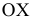
На рис. 2.20 показано построение следов прямой 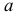
Построение горизонтального и фронтального следов выполняют по правилам, указанным выше, профильный след 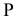
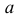
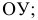
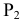
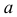
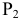
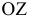
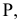
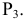
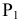
Взаимное положение прямых
Прямые в пространстве могут занимать различное взаимное положение. Они могут быть параллельными, пересекающимися и скрещивающимися.
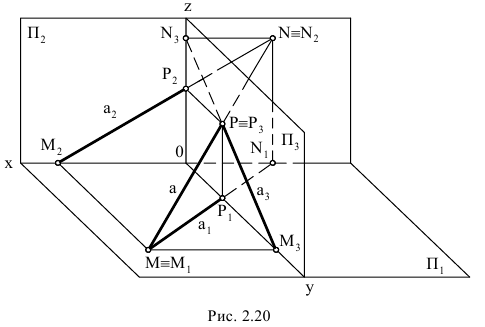
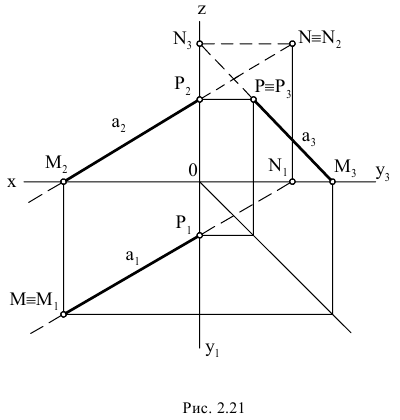
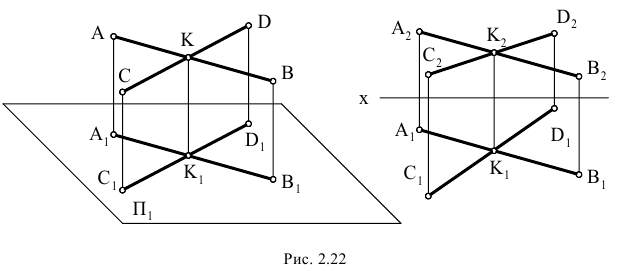
Если прямые в пространстве пересекаются, то на эпюре их одноименные проекции пересекаются, и точки пересечения проекций этих прямых лежат на одной линии связи (рис. 2.22).
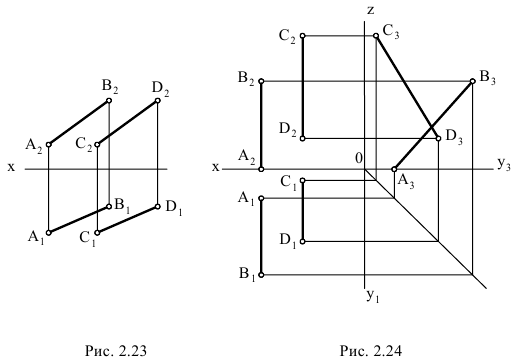
Если прямые в пространстве параллельны, то на эпюре их одноименные проекции параллельны. На рис. 2.23 изображены прямые общего положения 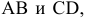
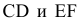
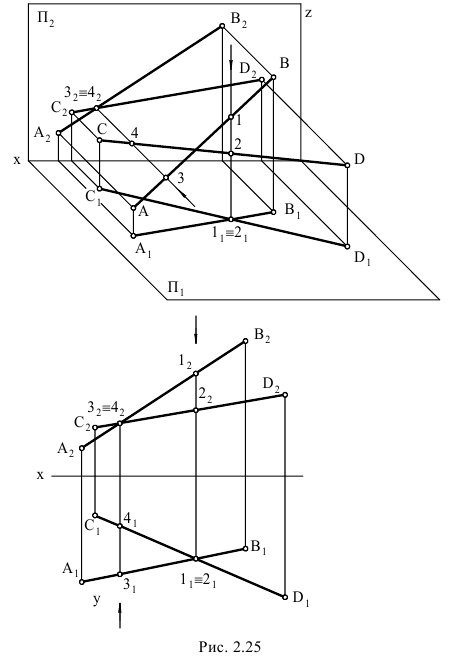
Если прямые в пространстве не пересекаются и не параллельны между собой, то такие прямые называются скрещивающимися. На эпюре точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи. Эти точки не являются общими для прямых (рис. 2.25). Точка пересечения одноименных проекций скрещивающихся прямых является на эпюре проекцией двух конкурирующих точек, принадлежащих заданным прямым.
Из чертежа видно, что расстояния от плоскости 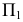
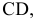

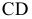
Точке пересечения фронтальных проекций соответствуют точки 3 и 4, расположенные на прямых 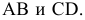
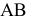
Проекции плоских углов
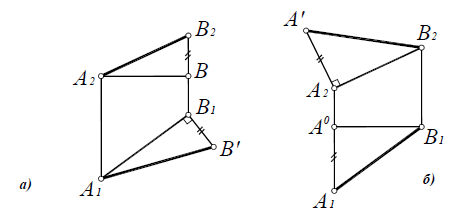
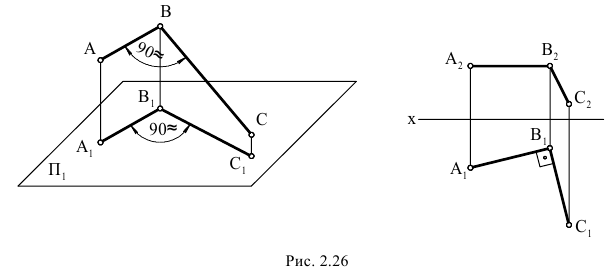
Плоский угол проецируется на плоскость проекций в натуральную величину, если его стороны параллельны этой плоскости проекций.
Для того чтобы прямой угол проецировался на плоскость в натуральную величину, необходимо и достаточно, чтобы одна из его сторон была параллельна, а другая не перпендикулярна плоскости проекций. Изображенный на рис. 2.26 угол 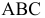
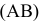
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.