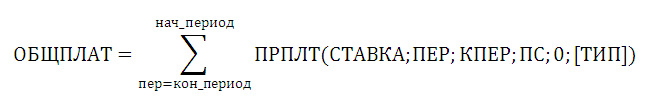как рассчитать сумму процентов по кредиту с помощью excel
Аннуитет. Расчет в EXCEL выплаченных процентов за период
history 2 февраля 2015 г.
Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат. В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа) показано как рассчитать величину регулярной суммы для погашения кредита или ссуды. В данной статье научимся вычислять сумму процентов, которую необходимо выплатитьпосле заданного количества периодов (а также сумму процентов, которую необходимо выплатить в промежутке между произвольно заданными периодами). Данные расчеты можно сделать несколькими разными способами (см. файл примера ).
Вычисление суммы процентов, которую необходимо выплатитьпосле заданного количества периодов
Чтобы вычислить, сколько процентов нужно будет выплатитьс момента предоставления займа, после истечения заданного количества периодов, используйте формулу: ОБЩПЛАТ(ставка; кол_пер; нз; 1; кон_период; тип).
Задача1. Предположим, что заем 1 млн. был выдан на 5 лет. Годовая ставка = 10%. Начисление процентов и погашение займа происходит ежемесячно в конце месяца (тип=0). Определить сколько процентов будет выплачено банку по прошествии 2-х лет. Решение1. = ОБЩПЛАТ(10%/12; 5*12; 1 000 000; 1; 2*12; 0)
Задача2. Предположим, что заем 2 млн. был выдан на 3 года. Годовая ставка = 7%. Начисление процентов и погашение займа происходит ежеквартально в начале месяца (тип=1). Определить сколько процентов будет выплачено банку по прошествии 1-го года. Решение2. = ОБЩПЛАТ(7%/4; 3*4; 2 000 000; 1; 1*4; 1)
Вычисление суммы процентов, которую необходимо выплатить в промежутке между 2-мя периодами
Способ 1. Функция ОБЩПЛАТ()
Функция ОБЩПЛАТ(ставка; кол_пер; нз; нач_период; кон_период; тип) возвращает кумулятивную (нарастающим итогом) величину процентов, выплачиваемых по займу в промежутке между двумя периодами выплат ( нач_период и кон_период ).
Примечание . Английская версия: CUMIPMT(rate, nper, pv, start_period, end_period, type) returns the CUMulative Interest paid on a loan between start_period and end_period.
Альтернативная формула:
Из анализа альтернативной формулы ясно, что функция ОБЩПЛАТ() может использоваться, только если БС=0, т.е. когда предполагается, что по прошествии количества периодов «Кол_пер» займ полностью погашается. Также обратите внимание, что в определении функции ОБЩПЛАТ() речь идет только о займе. Определить сумму, накопленную за счет процентов в случае срочного вклада, с помощью функции ОБЩПЛАТ() не получится (для этого см. Способ 2).
Способ 2. Функция ПРПЛТ()
Чтобы вычислить сумму процентов, которая была выплачена в промежутке между двумя произвольными периодами нач_период и кон_период используйте формулу: =СУММПРОИЗВ(ПРПЛТ(ставка;СТРОКА(ДВССЫЛ(нач_период&»:»&кон_период)); кпер; пс; [бс]; [тип]))
Как рассчитать проценты по кредиту в Excel без специальных знаний
Часто прописанные в кредитном договоре величины и числа не вызывают доверия. Проверить их можно с помощью программы MO Excel, применив, в зависимости от вопроса, одну из финансовых функций.
Аннуитетные платежи по кредитному договору: как рассчитать в Excel
Как предполагается, по аннуитетной схеме клиенту необходимо вносить для погашения задолженности равные суммы в течение срока договора с кредитной организацией. Для того чтобы рассчитать такие платежи, в программе есть специальная функция – ПЛТ. Ее использование требует создание новой таблицы и ввода данных в любой ячейке поля.
Например, был выдан кредит на сумму 100 тысяч рублей под 15% годовых на два года. Соответственно, в ячейке необходимо отразить выражение:
В скобках после наименования данные вводятся в определенном порядке:
Плата процентов по кредиту
Знак минуса перед суммой означает, что данное число представляет собой обязательство. Если это единичный расчет, ставить его необязательно. Но если число в дальнейшем используется в других формулах, он важен. Процентная ставка может быть отражена десятичной дробью (15% годовых = 0,0125).
Расчет таких платежей позволит проверить, насколько правильно сотрудниками банка определен ежемесячный платеж клиента.
Расчет дифференцированных платежей в программе MO Excel
При выборе дифференцированного варианта возврата денег банку клиент теряет намного меньше, так как проценты с каждым разом уменьшаются. Банки же такой вариант предлагают реже. Но и для лица этот вариант менее удобен, так как регулярно нужно рассчитывать новую сумму к оплате.
В основу снова ляжет пример. Клиент взял в банке 180 тысяч рублей на 3 года. Ставка – 13% годовых. Погашение предполагается каждый месяц, в конце периода.
Для расчетов необходимо узнать ежемесячную базовую сумму, подлежащую выплате. Каждый месяц клиент обязан возвращать банку равную сумму – часть долга. В рассматриваемом случае это 180000 / 3 / 12 = 5000 рублей. Каждый месяц на остаток начисляются прописанные в договоре проценты. Соответственно, уменьшается остаток – меньше становится и сумма, начисляемая банком.
Расчет основывается на функции ПРОЦПЛАТ. Через точку с запятой в ней обозначаются четыре показателя:
Расчет процентов по кредиту
Функция ПРОЦПЛАТ совпадает по аргументам с предыдущей формулой, однако не имеет с ней ничего схожего, подменять их друг другом нельзя. В англоязычной версии наименование функции – ISPMT, аргументы в ней такие же.
В ПРОЦПЛАТ предполагается начисление суммы процентов в начале периода. Сдвинуть эту функцию на конец месяца можно, если сместить вычисления на период раньше (не «период», а «период-1»). Итоги будут отображены с противоположным знаком, то есть минусом. Таким образом отличаются расчеты при начислении процентов по кредиту и вкладу.
Формула определения суммы процентов по взятому кредиту
Вычисление сумм, перечисляемых на погашение процентов, возможно с использованием функции ПРПЛТ. Ее аргументы не отличаются от необходимых в ОСПЛТ:
Такие расчеты подходят для аннуитетных платежей, когда не известно тело кредита. Определить процент при дифференцированной схеме начисления процентов можно, узнав, какие денежные средства направляются ежемесячно на погашение задолженности.
От суммы ежемесячного платежа необходимо отнять то самое тело кредита, направляемое на погашение непосредственно занятой у банка суммы. Разница и будет процентами, постепенно снижающимися при дифференцированном порядке их начисления.
Установление полной стоимости кредита в программе
Формула для определения ставки по кредиту рекомендована Центробанком России. Ее возможно посчитать, если использовать формулу, указанную в письме ФНС.
Для понимания вопроса необходимы многочисленные данные:
В процессе определения стоимости кредита (т.е. связанные с ним суммы за выдачу кредита или первоначальное рассмотрение заявки) важно отразить все дополнительные расходы, например, за выдачу, чтобы сумма стала максимально корректной.
Полную стоимость при исчислении составляют:
Самостоятельный расчет выплат
С целью расчетов установлена новая формула, которая уже давно используется за рубежом для установления эффективной годовой ставки.
В подходящую формулу входят:
Законодательные рекомендации в данном аспекте окончательно не сформированы. Однако функция уже действует.
Таким образом, финансовые функции Excel позволяют проверить отсутствие переплат ввиду ошибок и огрех в договоре, случайных или намеренных. Каждый шаблон не требует тяжело получаемых данных, поэтому удобен в применении.
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Аннуитет. Определяем процентную ставку в EXCEL
history 2 февраля 2015 г.
Пусть известна сумма и срок кредита, а также величина регулярного аннуитетного платежа. Рассчитаем в MS EXCEL под какую процентную ставку нужно взять этот кредит, чтобы полностью его погасить за заданный срок. Также в статье разберем случай накопления вклада.
Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение]) возвращает процентную ставку по аннуитету.
]]> Вот что написано на сайте MS ]]> : Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1 (подробнее см. обзорную статью о функциях аннуитета ).
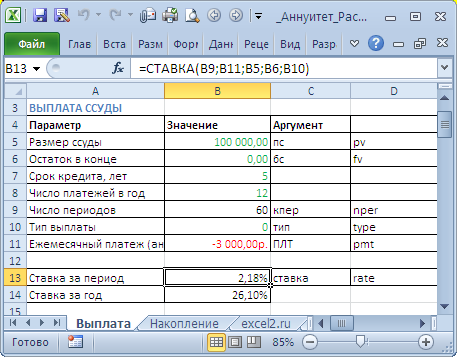
Задача1 – Выплата кредита
Определим под какую годовую ставку мы можем взять 100 000 руб., выплачивая ежемесячно 3000 руб. в течение 5 лет.
В условии задачи содержится следующая информация:
Формула может вернуть отрицательные значения ставки. Это происходит, когда сумма всех регулярных платежей недостаточна для погашения кредита даже при 0 ставке. Но, в нашем случае все в порядке: 60*(3000)=180000>100000. Отрицательная ставка означает, что банк выплачивает нам проценты за пользование кредитом, что является абсурдом. Это, конечно, ошибка (попробуйте например, в файле примера на Листе Выплата установить платеж =-1000).
Если задать платеж = 0 или того же знака, что и сумма кредита, то функция СТАВКА() вернет ошибку #ЧИСЛО! Это и понятно, при нулевых платежах погасить кредит невозможно.
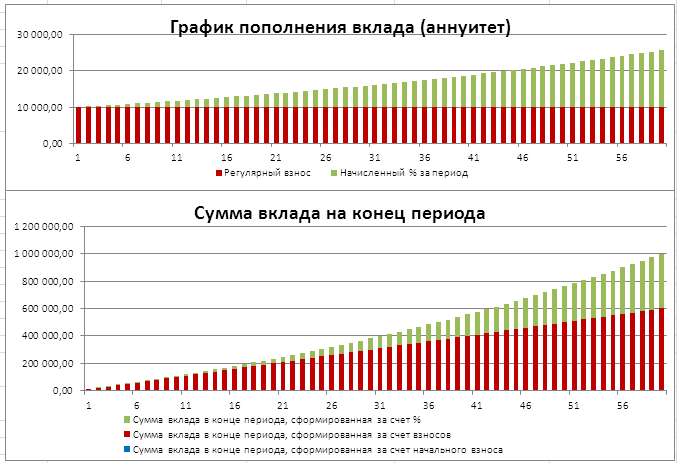
Задача2 – Накопление суммы вклада
Определим, с какой годовой ставкой мы можем накопить 1 000 000 руб., внося ежемесячно по 10 000 руб. в течение 5 лет. (см. файл примера на Лист Накопление )
Формула для вычисления годовой ставки будет выглядеть так =12*СТАВКА(12*5;-10000;0;1000000) =19,38%
Здесь ПС=0, т.е. начальная сумма вклада =0 ( Приведенная Стоимость ). Целевой вклад = 1000000 (БС – Будущая Стоимость ).
Если суммарное количество взносов будет > целевой стоимости (1000000), то ставка станет отрицательной, чтобы соблюсти наше требование БС=1000000.
Если задать величину пополнения = 0 или того же знака, что и целевая сумма, то функция СТАВКА() вернет ошибку #ЧИСЛО! Это и понятно, при нулевых взносах накопить ничего не получится. Взнос того же знака, что и целевая сумма, вероятно, означает, что банк платит нам. Но, это не возможно, т.к. начальная сумма вклада =0, поэтому выдается ошибка.
Использование формул Excel для определения объемов платежей и сбережений
Управление личными финансами может быть сложной задачей, особенно если вам нужно планировать свои платежи и сбережения. Excel формулы и шаблоны бюджетов помогут вам вычислить будущую стоимость своих задолженности и инвестиций, что упростит расчет времени, необходимого для достижения целей. Используйте следующие функции:
ПЛТ: возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и процентной ставки.
КПЕР: возвращает количество периодов выплаты для инвестиции на основе регулярных постоянных выплат и постоянной процентной ставки.
ПВ: возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат.
БС: возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.
Расчет ежемесячных платежей для погашения задолженности по кредитной карте
Предположим, остаток к оплате составляет 5400 долларов США под 17% годовых. Пока задолженность не будет погашена полностью, вы не сможете рассчитываться картой за покупки.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
получаем ежемесячный платеж в размере 266,99 долларов США, который позволит погасить задолженность за два года.
Аргумент «ставка» — это процентная ставка на период погашения кредита. Например, в данной формуле ставка 17% годовых делится на 12 — количество месяцев в году.
Аргумент КПЕР 2*12 — это общее количество периодов выплат по кредиту.
Аргумент ПС или приведенной стоимости составляет 5400 долларов США.
Расчет ежемесячных платежей по ипотеке
Представьте дом стоимостью 180 000 долларов США под 5% годовых на 30 лет.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
получена сумма ежемесячного платежа (без учета страховки и налогов) в размере 966,28 долларов США.
Аргумент «ставка» составляет 5%, разделенных на 12 месяцев в году.
Аргумент КПЕР составляет 30*12 для ипотечного кредита сроком на 30 лет с 12 ежемесячными платежами, оплачиваемыми в течение года.
Аргумент ПС составляет 180 000 (нынешняя величина кредита).
Расчет суммы ежемесячных сбережений, необходимой для отпуска
Необходимо собрать деньги на отпуск стоимостью 8500 долларов США за три года. Процентная ставка сбережений составляет 1,5%.
С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)
получаем, что чтобы собрать 8500 долларов США за три года, необходимо откладывать по 230,99 долларов США ежемесячно.
Аргумент «ставка» составляет 1,5%, разделенных на 12 месяцев — количество месяцев в году.
Аргумент КПЕР составляет 3*12 для двенадцати ежемесячных платежей за три года.
Аргумент ПС (приведенная стоимость) составляет 0, поскольку отсчет начинается с нуля.
Аргумент БС (будущая стоимость), которую необходимо достичь, составляет 8500 долларов США.
Теперь допустим, вы хотите собрать 8500 долларов США на отпуск за три года, и вам интересно, какую сумму необходимо положить на счет, чтобы ежемесячный взнос составлял 175,00 долларов США. Функция ПС рассчитает размер начального депозита, который позволит собрать желаемую сумму.
С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)
мы узнаем, что необходим начальный депозит в размере 1969,62 долларов США, чтобы можно было откладывать по 175,00 долларов США в месяц и собрать 8500 долларов США за три года.
Аргумент «Ставка» составляет 1,5%/12.
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
Аргумент БС (будущая стоимость) составляет 8500.
Расчет срока погашения потребительского кредита
Представьте, что вы взяли потребительский кредит на сумму 2500 долларов США и согласились выплачивать по 150 долларов США ежемесячно под 3% годовых.
С помощью функции КПЕР(ставка;ПЛТ;ПС)
выясняем, что для погашения кредита необходимо 17 месяцев и несколько дней.
Аргумент «Ставка» составляет 3%/12 ежемесячных платежей за год.
Аргумент ПС (приведенная стоимость) составляет 2500.
Расчет суммы первого взноса
Скажем, вы хотите приобрести автомобиль стоимостью 19 000 долларов США под 2,9 % годовых за три года. Вы хотите, чтобы ежемесячные платежи были на уровне 3500 долларов США в месяц, поэтому вам нужно выяснить сумму своего взноса. В этой формуле результатом функции ПС является сумма займа, которая затем вычитается из цены покупки, чтобы получить первый взнос.
С помощью функции ПС(ставка;КПЕР;ПЛТ)
выясняем, что первый взнос должен составлять 6946,48 долларов США.
Сначала в формуле указывается цена покупки в размере 19 000 долларов США. Результат функции ПС будет вычтен из цены покупки.
Аргумент «Ставка» составляет 2,9%, разделенных на 12.
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
Оценка динамики увеличения сбережений
Начиная с 500 долларов США на счету, сколько можно собрать за 10 месяцев, если класть на депозит по 200 долларов США в месяц под 1,5% годовых?
С помощью функции БС(ставка;КПЕР;ПЛТ;ПС)
получаем, что за 10 месяцев выйдет сумма 2517,57 долларов США.
Аргумент «Ставка» составляет 1,5%/12.
Аргумент КПЕР составляет 10 (месяцев).
Формула для расчета аннуитетного платежа в Excel
Платежи по кредитам удобнее и быстрее рассчитывать с Microsoft Office Excel. На ручное вычисление уходит гораздо больше времени. В данной статье речь пойдет об аннуитетных платежах, особенностях их расчета, преимуществах и недостатках.
Что такое аннуитетный платеж
Способ ежемесячного погашения кредита, при котором вносимая сумма не меняется в течение всего времени кредитования. Т.е. человек по определенным числам каждого месяца вносит конкретную сумму денег до тех пор, пока полностью не погасит кредит.
Причем проценты по кредиту уже включены в общую сумму, вносимую в банк.
Классификация аннуитета
Аннуитетные платежи можно разделить на следующие виды:
Обратите внимание! Фиксируемые платежи предпочтительнее для всех заемщиков, т.к. имеют небольшой риск.
Преимущества и недостатки аннуитетных платежей
Чтобы лучше разбираться в теме, необходимо изучить ключевые особенности данного типа кредитных платежей. Он имеет следующие преимущества:
Без недостатков не обошлось:
Из чего состоит платеж по кредиту?
Аннуитетный платеж имеет следующие составляющие части:
В итоге общее количество процентов практически всегда превышает вносимую заемщиком сумму для уменьшения долга.
Основная формула аннуитетного платежа в Excel
Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:
Важно! Раскрывать скобки в знаменателе данного выражения для его упрощения нельзя.
Основные значения формулы расшифровываются так:
Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.
Примеры использования функции ПЛТ в Excel
Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:
Дополнительная информация! Отрицательное число свидетельствует о том, что заемщик расходует деньги.
Пример расчета суммы переплаты по кредиту в Excel
В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:
Формула вычисления оптимального ежемесячного платежа по кредиту в Excel
Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:
Обратите внимание! Таким образом, чтобы на счету клиенту через 4 года накопилось 2000000 рублей по ставке 11%, ему нужно каждый месяц вносить по 28188 рублей. Минус в сумме свидетельствует о том, что клиент несет убытки, отдавая деньги в банк.
Особенности использования функции ПЛТ в Excel
В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; [бс]; [тип]). У функции есть следующие особенности:
Расчет оплаты
В общем виде оплата по аннуитету рассчитывается в два этапа. Чтобы разбираться в теме, каждый из этапов необходимо рассмотреть по отдельности. Об этом пойдет речь далее.
Этап 1: расчет ежемесячного взноса
Чтобы в Excel посчитать сумму, которую нужно вносить каждый месяц по кредиту с фиксируемой ставкой, необходимо:
Важно! После расчета взноса можно будет рассчитать сумму, которую переплатит заемщик за весь период кредитования.
Этап 2: детализация платежей
Сумму переплаты можно посчитать помесячно. В итоге человек поймет, сколько денег каждый месяц он будет тратить на кредит. Расчет по детализации выполняется следующим образом:
Дополнительная информация! При расчете остатка на формулу надо навешивать знаки долларов, чтобы она не съехала при растягивании.
Расчет аннуитетных платежей по кредиту в Excel
За вычисление аннуитета в Excel отвечает функция ПЛТ. Принцип вычисления в общем виде заключается в выполнении следующих шагов:
Расчет в MS Excel погашение основной суммы долга
Аннуитетные платежи должны вноситься ежемесячно определенными суммами. Причем процентная ставка не изменяется.
Вычисление остатка суммы основного долга (при БС=0, тип=0)
Предположим, что кредит на 100000 рублей берется на 10 лет под 9%. Необходимо рассчитать сумму основного долга в 1 месяце 3-го года. Решение:
Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами
Такой расчет лучше сделать простым способом. Нужно использовать следующие формулы для вычисления суммы в промежутке за два периода:
Обратите внимание! Буквы в скобках заменяются конкретными значениями.
Досрочное погашение с уменьшением срока или выплаты
Если потребуется уменьшить срок кредитования, то придется производить дополнительные вычисления с помощью оператора ЕСЛИ. Так можно будет контролировать нулевой баланс, который не должен быть достигнут раньше окончания сроков выплаты.
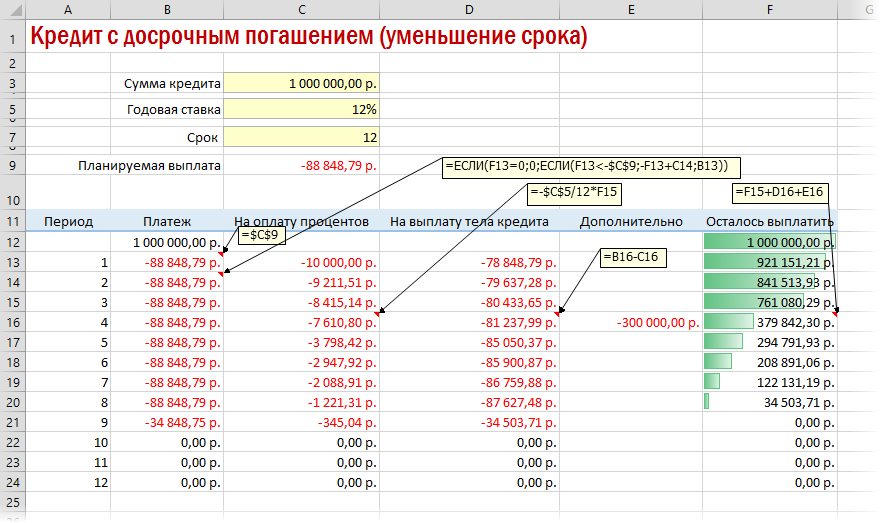
Чтобы снизить выплаты, нужно пересчитывать взнос за каждый предыдущий месяц.
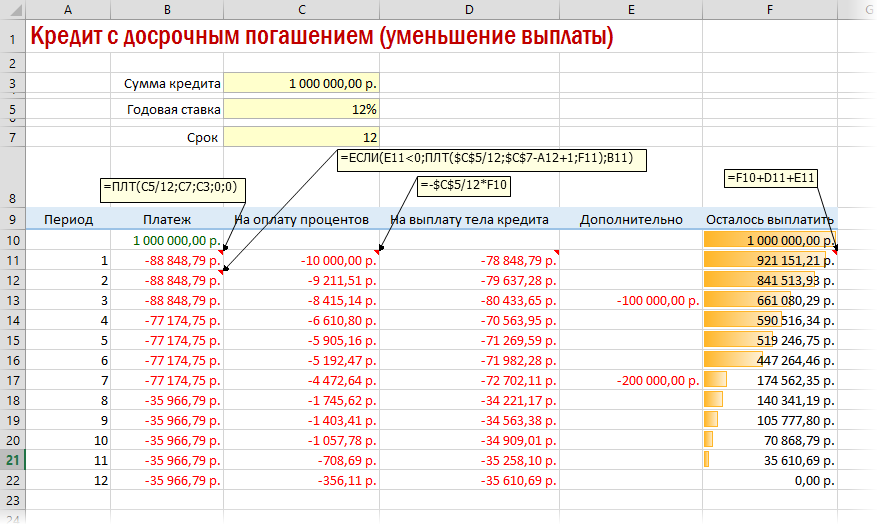
Кредитный калькулятор с нерегулярными выплатами
Есть несколько вариантов аннуитета, когда заемщик может вносить нефиксированные суммы в любой день месяца. В такой ситуации остаток долга и проценты считаются за каждый день. При этом в Экселе надо:
Расчет периодического платежа в MS Excel. Срочный вклад
В Excel можно быстро посчитать размер регулярных выплат при условии, что уже накопилась фиксированная сумма. Данное действие выполняется с использованием функции ПЛТ после составления исходной таблицы.
Заключение
Таким образом, аннуитетные платежи проще, быстрее и эффективнее рассчитывать именно в Эксель. За их вычисление отвечает оператор ПЛТ. С подробными примерами можно ознакомиться выше.