как рассчитывается передаточное отношение ременной передачи

26.10.202321.11.2022 admin 0 Comments

Как рассчитывается передаточное отношение ременной передачи

Статьи

Как осуществляется расчет ременного привода, и почему это важно

Любой ременной привод состоит из 3 основных элементов: двух шкивов (валов) – ведущего и ведомого, а также соединяющего их ремня, который и передает вращение первого вала второму. На практике столь простая конструкция требует определенных знаний и предварительных расчетов. Неправильный, непродуманный подбор компонентов грозит падением КПД из-за проскальзывания ремня на валах и его быстрому износу, что ведет к незапланированной остановке производственной линии и, как следствие, упущенной прибыли. О том, как осуществляется расчет ременного привода мы сегодня и поговорим.

Основные параметры

Параметрами, служащими основой для расчета ременной передачи, являются:

Стандартный способ расчета

Расчет производится в стандартной последовательности:

Сложности

Несмотря на то, что вычисления на каждом этапе производятся по стандартным формулам и с учетом табличных значений из действующих ГОСТов, расчет ременного привода дополнительно осложняется рядом других параметров, к примеру:

Дополнительно стоит отметить, что вышеприведенный порядок расчетов справедлив для открытой ременной передачи с плоским ремнем. Соответственно, при использовании другого вида передачи, к примеру, перекрестной или угловой, а также зубчато-ременной, используются другие формулы и методики расчетов.

С учетом всего вышесказанного, непрофессионалу на практике подобрать подходящий приводной ремень оказывается крайне сложно.

Альтернативы

Использовать онлайн-калькулятор. При всей простоте – достаточно ввести исходные данные и получить основные расчетные параметры нажатием одной кнопки – этот вариант достаточно сложно рекомендовать.

Во-первых, все расчеты производятся в закрытом виде, поэтому гарантировать их правильность никто не может. Вполне возможно, что в калькуляторе могут использоваться неправильные формулы, при этом сайты, предлагающие подобные калькуляторы, никакой ответственности не несут, и если подобранный таким способом ремень вам не подойдет, «виноваты» в этом окажетесь только вы.

Во-вторых, калькулятор может просто не выдавать ряда нужных параметров, и получить их будет попросту негде.

Доверить расчеты профессионалам. Мы в «ДайвБелтСистем» крайне ответственно подходим к реализации конвейерных лент и ремней, и для нас очень важно, чтобы приобретаемая у нас продукция прослужила на вашем производстве как можно дольше. Именно поэтому мы не только предлагаем изделия от ведущих мировых компаний, но и оказываем ряд дополнительных услуг, в том числе, и расчет привода специалистами нашего инженерного отдела. При этом, в отличие от онлайн-калькулятора, мы можем гарантировать правильность и полноту расчетов и, как следствие, идеальный подбор ремня под ваши нужды.

» data-title=»Как осуществляется расчет ременного привода, и почему это важно» data-background=»none;» data-options=»small,square,line,horizontal,nocounter,sepcounter=1,theme=14″ data-services=»vkontakte,odnoklassniki,facebook,twitter,google,moimir»>

Источник

Передаточное отношение

Одной из важнейших кинематических характеристик в теории механизмов и машин является передаточное отношение. Оно позволяет определить, на какую величину возрастает момент приложенной силы, когда происходит передача вращения от одной детали к другой. На практике для решения различных технических задач механизмы создаются с кинематической схемой, имеющей постоянное или переменное передаточное отношение.

Общее определение

Значение передаточного отношения у кинематических схем рассчитывается по стандартному математическому выражению. Результат получается при проведении математической операции деления значения угловой скорости ведущего вала или шестерёнки, на такой же параметр ведомого вала. Вместо этих значений используют отношение их частот вращения.

Современные кинематические схемы реализованы с использованием следующих механических соединений:

Передача вращения основана на двух физических принципах: с помощью силы трения, с использованием механизмов зацепления. В зависимости от решаемой задачи механизмы изготавливаются с замедлением и ускорением. Первые называются редукторами, вторые — мультипликаторами. Обе разновидности бывают одноступенчатыми, двухступенчатыми, многоступенчатыми.

Пространственное расположение осей определяет следующие виды механизмов:

Все типы механизмов бывают замедляющие и ускоряющие движение. Наиболее частое применение замедляющих конструкций объясняется более высокой скоростью используемых двигателей и необходимостью увеличить мощность выходного элемента кинематической схемы.

В зависимости от соотношения скоростей возникает вопрос: может ли передаточное отношение быть отрицательным? Этот коэффициент является отношением величин имеющих только положительные значения. Он не может быть отрицательным. В зависимости от отношения числителя к знаменателю результат получиться больше единицы или меньше. В первом случает, он справедлив для редукторов, во втором для мультипликаторов.

Таблица передаточных отношений является сводным документом. В ней приведены значения основных технических характеристик всех типов кинематических соединений.

В сводной таблице можно найти зависимость значения передаточного числа от допустимой мощности, которая передаётся конкретным видом соединения.

Зубчатая передача

Это механическое соединение двух или более вращающихся валов при помощи специальных колёс, на поверхности которых выточены зубья. Такой тип подразделяется по следующим характеристикам:

Важную роль в понимании работы всего механизма играет передаточное отношение зубчатой передачи. Его вычисляют, используя классическое выражение. Оно находится с подстановкой различных параметров. Например, подсчитывая численность изготовленных зубьев на ведущем и ведомом колесе. Формула позволяет получать результаты с высокой степенью точности:

Где i₁₂ — передаточное отношение от звена 1 к звену 2 (звено 1 — ведущее, звено 2 — ведомое; d₁,d₂ — диаметры звеньев; z₁, z₂ — количество зубьев звеньев (если таковые имеются); M1, M2 — крутящие моменты звеньев; ω₁, ω₂ — угловые скорости звеньев; n₁, n₂ — частоты вращения звеньев.

В большей степени он зависит от количества зубьев расположенных на шестерёнке. Существенным достоинством зубчатого соединения является постоянство расчётного и реального передаточного отношения. Она связано с отсутствием эффекта проскальзывания.

Существенное влияние на величину этого показателя оказывает применяемое количество шестерней и число зубчатых колёс.

Для цилиндрической передачи этот параметр кроме приведенных выше параметров зависит от межосевого расстояния. Цилиндрические зубчатые передачи распространены в различных агрегатах легковых и грузовых автомобилей, тракторов, сельскохозяйственной техники. Их активно используют в трансмиссии.

Зубчатая передача обладает самым большим коэффициентом передачи мощности. Она способна отдавать мощность до 4500 кВт с передаточным числом достигающим 6,3.

Распространение получили зубчатые конструкции конического типа. Они обладают ортогональным сочленением. Расчёт конической передачи предполагает учёт таких параметров как: делительные диаметры, углы конусов, количество зубьев.

Для получения поступательного движения применяется реечное соединение. Конструктивно она состоит из шестерёнки, рейки с нанесёнными зубьями. Для реечной передачи учитывают диаметр окружности и количество зубьев на колесе, число зубьев расположенных на рейке.

Планетарная передача

Широко применяется так называемая планетарная кинематическая схема. Она представляет собой механизм, предназначенный для передачи, преобразования вращательного движения. С этой целью используются зубчатые колеса, расположенные на перемещающейся оси. Конструктивными элементами являются: центральные зубчатые колеса, закреплённые на неподвижных осях, боковые зубчатые колеса (расположены на перемещающихся осях). Для обеспечения наилучшего эффекта планетарные механизмы изготовляются на параллельных осях.

Максимальное значение передаточного числа достигает 9 единиц.

Коэффициент полезного действия достаточно высокий. Его значение приближается к 0,98. Наиболее распространёнными являются конструкции, в которых применяются нескольких сателлитов. Их располагают с угловыми шагами равной величины.

Такие конструкции выполняются с постоянным или переменным передаточным отношением. Некоторые из них имеют возможность регулировки этого параметра. Они разработаны обратимыми и необратимыми. В обратимых образцах предусмотрено движение в прямом и обратном направлении. В необратимых конструкциях такое движение невозможно. Изменение передаточного отношения бывает ступенчатым или бесступенчатым. Ярким представителем первого агрегата является механическая коробка передач автомобиля. Второй вариант применяется в вариаторах.

Рассмотренные передаточные отношения передач рассчитываются на этапе проектирования агрегата при выборе кинематической схемы. С их помощью производится выбор типа соединения, определяется эффективность. Оценивается надёжность всего механизма.

Цепная передача

Хорошо известна цепная передача. Она относится к гибким конструкциям. Передаточное отношение цепной передачи рассчитывается расчёту зубчатых систем. Ведущая и ведомая звёздочка рассматриваются как зубчатые колеса. Значение этого параметра достигает 15.

Особенностью такой конструкции считается требование иметь определённое провисание цепи. Настройка этого параметра проводится с помощью специального регулирующего винта.

Достоинства подобного соединения сводятся к следующему:

К недостаткам можно отнести быстрый износ соединительных элементов цепи. Это требует периодической смазки. Вторым недостатком считается высокий уровень шума.

Кроме передаточного числа для них рассчитывается величина статистической разрушающей силы. Этот параметр зависит от требуемого коэффициента безопасности. Его задают в интервале от 6 до 10. Он обеспечивает качественную работу всего механизма, высокую надёжность соединения и долговечность.

Червячная передача

Необходимость изменения вращательного движения под углом требует создания специального вида систем. К таким конструкциям относится червячная передача. Основной элемент такой передачи может быть цилиндрической формы, глобоидным, эвольвентным, архимедовым винтом. Это зависит от поверхности, на которой расположена резьба, и профиля резьбы.

В качестве параметров, используемых для расчёта передаточного числа подставляемых в выражение, используют существующее количество заходов червячного механизма. Обычно оно варьируется от одного до четырёх. Таблица передаточных отношений для червячной схемы позволяет рассчитать необходимое количество элементов зацепления. Приведенные в этой таблице данные, помогают правильно выбрать соединения для конкретного механизма.

Основными недостатками передачи являются:

Ременная передача

Данная конструкция является часто встречающейся. Её тип определяется расположением вала и направлением движения ремня. Их классифицируют следующим образом:

Для повышения надёжности применяют спаренное соединение. Реализация подобных конструкций производится с помощью ремней различного сечения. Наиболее популярными являются три типа: прямоугольные, в форме трапеции, круглого сечения.

Значение передаточного отношения рассчитывается подстановкой в классическую формулу скоростей вращения ведущего и ведомого валов. Иногда в расчёте используют число оборотов каждого из валов. В качестве альтернативного варианта при расчёте этого параметра используются величины диаметров (радиусов) шкивов.

Источник

Как рассчитывается передаточное отношение ременной передачи

Классификация передач. В зависимости от формы поперечного сечения ремня передачи бывают: плоскоременные, клиноременные, круглоременные, поликлиноременные (рис. 69). Плоскоременные передачи по расположению бывают перекрестные и полуперекрестные (угловые), рис. 70. В современном машиностроении наибольшее применение имеют клиновые и поликлиновые ремни. Передача с круглым ремнем имеет ограниченное применение (швейные машины, настольные станки, приборы).

Разновидность ременной передачи является Зубчатоременная, передающая нагрузку путем зацепления ремня со шкивами.

Рис. 70. Виды плоскоременных передач: а – перекрестная, Б – полуперекрестная (угловая)

Преимущества. Благодаря эластичности ремней передачи работают плавно, без ударов и бесшумно. Они предохраняют механизмы от перегрузки вследствие возможного проскальзывания ремней. Плоскоременные передачи применяют при больших межосевых расстояниях и, работающие при высоких скоростях ремня (до 100М/с). При малых межосевых расстояниях, больших передаточных отношениях и передаче вращения от одного ведущего шкива к нескольким ведомым предпочтительнее клиноременные передачи. Малая стоимость передач. Простота монтажа и обслуживания.

Недостатки. Большие габариты передач. Изменение передаточного отношения из-за проскальзывания ремня. Повышенные нагрузки на опоры валов со шкивами. Необходимость устройств для натяжения ремней. Невысокая долговечность ремня.

Сферы применения. Плоскоременная передача проще, но клиноременная обладает повышенной тяговой способностью и вписывается в меньшие габариты.

Круглоременные передачи применяют в небольших машинах, например машинах швейной и пищевой промышленности, настольных станках, а также различных приборах.

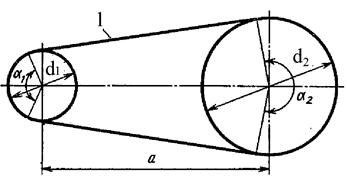
Рис. 71 Схема ременной передачи.

Силовой расчет. Окружная сила на ведущем шкиве

. (12.1)

Расчет ременных передач выполняют по расчетной окружной силе с учетом коэффициента динамической нагрузки И режима работы передачи:

, (12.2)

Где — коэффициент динамической нагрузки, который принимается =1 при спокойной нагрузке, =1,1 – умеренные колебания нагрузки, =1.25 – значительные колебания нагрузки, =1,5 – ударные нагрузки.

Начальную силу натяжения ремня FO (предварительное натяжение) принимают такой, чтобы ремень мог сохранять это натяжение достаточно длительное время, не подвергаясь большой вытяжке и не теряя требуемой долговечности. Соответственно этому начальное напряжение в ремне для плоских стандартных ремней без автоматических натяжных устройств =1,8МПа; с автоматическими натяжными устройствами = 2МПа; для клиновых стандартных ремней =1,2. 1,5МПа; для полиамидных ремней = 3. 4МПа.

Начальная сила натяжения ремня

, (12.3)

Силы натяжения ведущей И ведомой S2 Ветвей ремня в нагруженной передаче можно определить из условия равновесия шкива (рис. 72).

Рис. 72. Схема к силовому расчету передачи.

Из условия равновесия ведущего шкива

(12.4)

С учетом (12.2) окружная сила на ведущем шкиве

. (12.5)

Натяжение ведущей ветви

, (12.6)

Натяжение ведомой ветви

. (12.7)

Давление на вал ведущего шкива

. (12.8)

Зависимость между силами натяжения ведущей и ведомой ветвей приближенно определяют по формуле Эйлера, согласно которой натяжений концов гибкой, невесомой, нерастяжимой нити, охватывающей барабан связаны зависимостью

, (12.9)

Где — коэффициент трения между ремнем и шкивом, — угол обхвата шкива.

Среднее значение коэффициента трения для чугунных и стальных шкивов можно принимать: для резинотканевых ремней =0,35, для кожаных ремней = 0,22 и для хлопчатобумажных и шерстяных ремней = 0,3.

При определении сил трения в клиноременной передаче в формулы вместо – коэффициента, трения надо подставлять приведенный коэффициент трения для клиновых ремней

, (12.10)

Где — угол клина ремня .

При совместном рассмотрении приведенных силовых соотношений для ремня получим окружную силу на ведущем шкиве

, (12.11)

Где — коэффициент тяги, который определяется по зависимости

. (12.12)

Увеличение окружного усилия на ведущем шкиве можно достичь увеличением предварительного натяжения ремня либо повышением коэффициента тяги, который повышается с увеличением угла обхвата и коэффициента трения.

В таблицах со справочными данными по характеристикам ремней указаны их размеры с учетом необходимых коэффициентов тяги.

Геометрический расчет. Расчетная длина ремней при известном межосевом расстоянии и диаметрах шкивов (рис.71):

(12.13)

Где . Для конечных ремней длину окончательно согласовывают со стандартными длинами по ГОСТ. Для этого выполняют геометрический расчет согласно схемы показанной на рис.73.

Рис.73. Схема к геометрическому расчету ременной передачи

По окончательно установленной длине плоскоременной или клиноременной открытой передачи действительное межосевое расстояние передачи пои условии, что

Расчетные формулы без учета провисания и начальной деформации ремня.

Угол обхвата ведущего шкива ремнем в радианах:

, (12.14)

В градусах .

Для плоскоременной передачи рекомендуется , а для клиноременной .

Порядок выполнения проектного расчета. Для ременной передачи при проектном расчете по заданным параметрам (мощность, момент, угловая, скорость и передаточное отношение) определяются размеры ремня и приводного шкива, которые обеспечивают необходимую усталостную прочность ремня и критический коэффициент тяги при максимальном КПД. По выбранному диаметру ведущего шкива из геометрического расчета определяются остальные размеры:

Проектный расчет плоскоременной передачи по тяговой способности производят по допускаемому полезному напряжению, Которое определяют по кривым скольжения. В результате расчета определяется ширина ремня по формуле:

, (12.15)

Где — окружная сила в передаче; — допустимая удельная окружная сила, которая соответствует максимальному коэффициенту тяги, которая определяется при скорости ремня =10 м/с и угле обхвата =1800; — коэффициент расположения передачи в зависимости от угла наклона линии центров к горизонтальной линии: =1,0, 0,9, 0,8 для углов наклона =0…600, 60…800, 80…900; — коэффициент угла обхвата шкива ; — скоростной коэффициент: ; — коэффициент режима работы, который принимается: =1,0 спокойная нагрузка; =0,9 нагрузка с небольшими изменениями, =0,8 – нагрузка с большими колебаниями, =0,7 – ударные нагрузки.