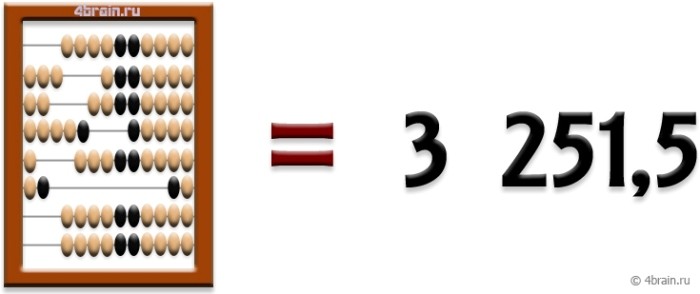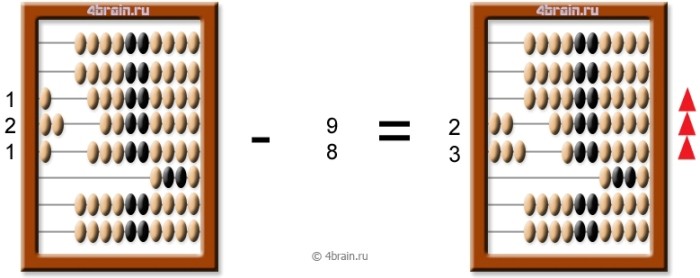как считать на старинных счетах
Как считать на счетах

В данной статье вы прочитаете, как научиться правильно считать на русских счетах. Вероятно, многие молодые люди ни разу не видели живьем такой арифметический инструмент, как счеты. А кто и видел, скорее всего, не знает, что с помощью этого инструмента можно научиться быстро складывать, вычитать и даже умножать и делить достаточно большие числа. Конечно, сегодня это не так актуально. Но в рамках раздела, посвященного устному счету, думаю, многим будет интересно прочитать о таком популярном приспособлении, облегчающем устный счет, но не исключающим его полностью.
Описание
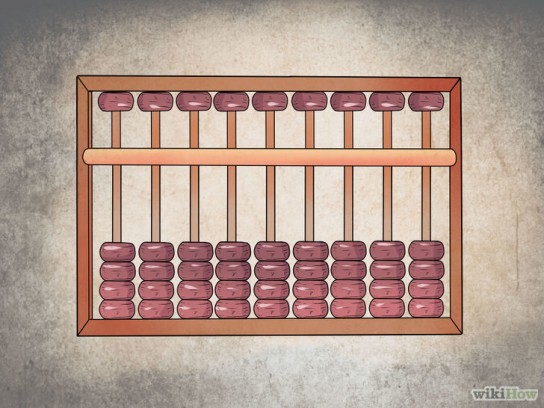
Знаменитые деревянные счеты, изображенные на рисунке ниже, повсеместно использовались в СССР первые две трети двадцатого века в основном для операций сложения и вычитания. Как же кассиры и бухгалтера пользовались этими русскими счетами? Давайте разберемся. Если же вы умеете пользоваться счетами, то можете перейти сразу к описанию более сложных операций.
В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть четвертаки (например, 25 копеек). Черным цветом выделены центральные костяшки (для удобства).
Набор числа. Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево. Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.
Но набор числа, это только начало. По-настоящему пользоваться деревянными счетами, значит совершать арифметические операции.
Сложение
Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов (именно с нижних!). Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы лучше разобраться, как правильно складывать числа на счетах, смотрите пример ниже (987 + 134 = 1 121):
Вычитание
Вычитание на счетах производится точно таким же образом, как сложение, – сверху вниз. Только если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число нехвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже смотрите пример, как правильно считать разность на русских счетах (121 – 98 = 23):
Умножение
Умножение на счетах является не самым быстрым и простым. В некоторых случаях, гораздо проще воспользоваться навыками быстрого умножения в уме. Однако в рамках данной статьи приведены некоторые методики умножения на деревянных счетах. Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой (при умножении на 2), и повторить эту процедуру при умножении на 3. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Что касается умножения на 5, как вы можете убедиться из этого урока, оно равносильно делению на 2 и последующему умножению на 10. В этом случае, после деления на 2 вы просто переносите разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.
Деление
Деление на русских счетах является достаточно сложной процедурой. Использовать для этого счеты иногда просто иррационально. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов и хорошего развития внимания и краткосрочной памяти.
Как пользоваться деревянными счетами?
В современном мире всё меняется с неконтролируемой скоростью и перемены захватывают практически все области человеческой жизни. Так произошло и в сфере бухгалтерии, где на помощь бухгалтерам вместо деревянных счётов пришли калькуляторы, существенно упрощающие и ускоряющие работу.
Сегодня резко уменьшается процент населения, которое владеет основами использования старых деревянных устройств, предназначенных для ведения подсчётов, а ведь ещё 20 лет назад счёты можно было встретить на столе у каждого бухгалтера. Сегодня же большинство людей при виде этих приспособлений задаются вопросами, как пользоваться деревянными счетами.
Немного исторических фактов
Счёты являются тем устройством, с которого и начиналась вся история вычислительных предметов. Ещё много столетий назад счёты пользовались мировой популярностью.
Первое вычислительное устройство именовалось «счётной доской». Особенности его использования практически не отличались в различных странах, а вот для изготовления счётов использовались различные материалы.
Что касается времён Древней Руси, то вычисления на первых порах производились посредством использования специальных косточек, группируемых в виде своеобразных кучек. В последующем произошла трансформация счётов, которые обзавелись дощатым видом. Первые счёты были представлены деревянной рамой с верёвочками, на которые нанизывались ягодные косточки.
Именно от последнего внешнего вида вычислительных предметов и отталкивались специалисты, разработавшие те счёты, которые известны практически каждому человеку.
С момента появления эти приспособления стали необычайно популярны, ведь они активно применялись во всех местах, связанных с финансами и необходимостью проведения вычислительных операций. Во времена Советского Союза практически каждый человек владел навыками работы со счётами.
Вычислительные операции с применением счётов
На первый взгляд может показаться, что считать с помощью столь примитивного устройства достаточно сложно, но это большое заблуждение, ведь опытные бухгалтера справлялись с этой задачей практически молниеносно.
Для начала следует понять, что собой представляет каждый ряд доски. Все ряды расположены по убыванию, что невозможно не заметить. При этом ряд с минимальным количеством костяшек должен быть самым нижним.
Вычислительные операции по сложению чисел предполагают следующее: для набора чисел следует воспользоваться для начала первым рядом, где на одной спице вверху расположены числа 10, 20, 30 и так далее. Посредством перемещения костяшек с левой части на правую выполняется набор необходимого числа.
После заполнения одного ряда на спице следует перейти к числам с большим значением. Так, 10 костяшек из нижнего ряда соизмеримы с одной, которая располагается в верхнем ряду. Вычислительные операции по сложению производятся посредством добавления костяшек к соответствующим рядам. Для подсчёта окончательного результата следует сложить все значения, начиная сверху.
Для вычитания чисел необходимо воспользоваться алгоритмом, расписанным выше, только проделывая манипуляции в обратном порядке, а именно с правой части на левую. К сожалению, к счётам не прилагается специальная инструкция, которую современный человек привык изучать при покупке оборудования, в особенностях работы которого он не сильно разбирается.
Информации относительно использования счётов не так уж много, поэтому для лучшего понимания всех нюансов рекомендуется изучать и видеоматериал, наглядно демонстрирующий всё, что написано в статьях.
Касательно процедур по сложению и вычетам всё понятно, а вот как быть с остальными вычислительными операциями? Сразу следует отметить, что операции по делению с помощью счётов никогда не пользовались популярностью, что связано со многими неудобствами. А вот для умножений чисел счёты всё-таки отлично подходят.
Так, для того чтобы умножить числа, одно из них следует сложить такое количество раз, которое требует второе число. Так, если необходимо умножить 1 на 2, то число 1 нужно сложить 2 раза. Если какое-либо число должно быть умножено на 5, понадобится перенос костяшек на верхний ряд и умножение на 10. Полученный результат следует мысленно делить на 2.
Если нужно умножать двухзначные числа, алгоритм операций немного другой. Так, множители должны быть разложены на составляющие части, над каждой из которых и рекомендуется проводить отдельные вычислительные операции.
К примеру, при необходимости умножить какое-либо число на 12 последнее следует разложить на 10 и 2. Последним этапом будет сложение результатов, полученных путём отдельного умножения числа на 10 и на 2.
Лучшее понимание основ работы со счётами приходит только с практикой, но у современного человека больше нет такой необходимости, ведь под рукой всегда найдутся более новые аналоги, которые гарантируют получение быстрых и правильных результатов.
История и общие понятия
Возможно, в это трудно поверить, но, несмотря на научно-технический прогресс, счеты абакус не считаются пережитком прошлого, активно используются по сей день в некоторых странах. К примеру, китайские и японские торговцы, применяющие механическое средство калькуляции для работы с большими числами, не являются редкостью, хотя эти страны не только не отстают, но и, напротив, лидируют в развитии, демонстрируя настоящее экономическое и техническое чудо.
Виды абакуса
Трудно найти более оптимальный инструмент для усвоения навыков ментальной арифметики, чем обычные счеты. Между тем подобные навыки помогают научиться быстро считать без использования таких популярных в последнее время вспомогательных средств, как электронный калькулятор, эксплуатация которого только ухудшает математические способности.
Неудивительно, что в древности люди считали гораздо лучше, чем их потомки, пусть даже и весьма примитивными способами. Так, долгое время в ход шли пальцы рук и ног, пока, наконец-то, не была придумана новая счетная система, дошедшая до настоящего времени, пусть и в усовершенствованном виде. Речь шла о прототипе абакуса, с помощью которого люди получили возможность выполнять более сложные вычисления.
Всего же сегодня выделяют три счетные системы, каждая из которых имеет свои особенности. В этот перечень входят:
Трудно переоценить роль абакуса в ментальной арифметике, поэтому неудивительно, что человечество неоднократно пробовало изменить счеты, пытаясь изобрести еще более удобное схематическое расположение костей и их количество на каждой палубе. Например, в 1958 году известный китайский ученый Ли Кай Чен разработал одноименную модификацию, представляющую собой своеобразный гибрид соробана и абакуса.
Устройство и основные элементы
Современные счеты, которые применяются на уроках ментальной математики, называются не только абакусом, но и абаком, а также линейкой. Все они в основном являются преемниками старого доброго японского соробана, практически не отличаясь друг от друга. Так, в классическом виде устройство состоит из следующих элементов:
Распределяются эти шарики и спицы в особом порядке, начиная свой отсчет с верхнего ряда справа налево. Увеличение чисел происходит в каждом последующем ряду посредством умножения на 10.
Правильное распределение бусин
Так как начальное значение у верхнего и нижнего ряда разные, то и их изменение в бо́льшую сторону будет происходить по индивидуальным схемам. Таблица числовых эквивалентов для каждой спицы выглядит следующим образом:
| Небесные бусины | Земные бусины | |
| Первый ряд | 5 | 1 |
| Второй | 50 | 10 |
| Третий | 500 | 100 |
| Четвертый | 5000 | 1000 |
| Пятый | 50 000 | 10 000 |
| Шестой | 500 000 | 100 000 |
| Седьмой | 5 000 000 | 1 000 000 |
| Восьмой | 50 000 000 | 10 000 000 |
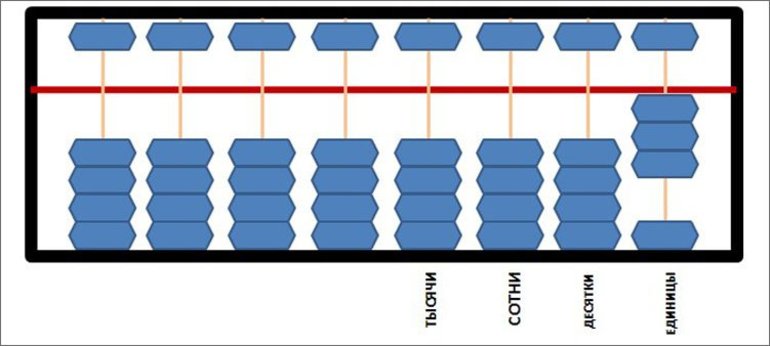
Еще проще ориентироваться по схематической картинке или названиям рядов, которые можно присваивать самостоятельно, облегчая тем самым процесс изучения особенностей счетного механизма. В качестве примера можно привести следующие условные обозначения рядов:
Чтобы понять, как правильно считать на абакусе, необходимо научиться распределять числа на нем. Базовый принцип распределения осуществляется исходя из следующих основных законов механического счета на абаке:
Поначалу освоение этой лесенки может показаться очень сложной задачей, но буквально через несколько минут интенсивной тренировки даже первоклассник покажет быстрый правильный набор и распределение, после чего можно приступать и к устному счету.
Инструкция по применению
Сегодня вовсе не обязательно посещать специальную школу для изучения устного счета на абакусе. Вместо этого можно попробовать онлайн-тренажеры с разными уровнями, предназначенные не только для начинающих, но и для продвинутых счетоводов.
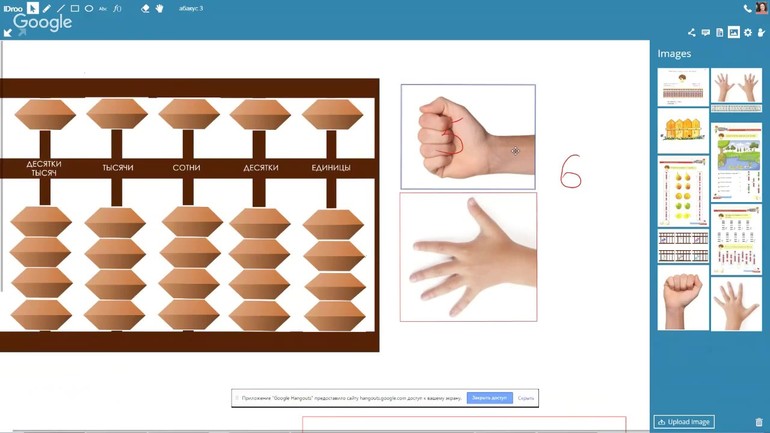
Положение пальцев и простые примеры
Вне зависимости от степени сложности выбранного задания, определяющее значение будет иметь положение пальцев, для чего была разработана специальная техника, облегчающая счет. Так, в случае применения японского абакуса необходимо задействовать только два пальца: указательный и большой. Согласно старинным схемам, большой палец предназначается для того, чтобы править костяшками из нижней палубы, тогда как указательный годится для всех бусин без исключения.
Кроме того, важную роль в этом вопросе играет и характер выполняемой счетной операции, ведь если, к примеру, речь идет о вычитании шариков земного ряда, то лучше всего делать его с помощью указательного пальца при прибавлении большим. В то же время для управления костяшками из небесной планки специалисты советуют ограничиваться одним только указательным пальцем, невзирая на то, что нужно сделать — прибавить или отнять.
Разобравшись с положением пальцев и кистей в целом, можно приступать к вычислению, начиная с установки счетов на горизонтальную поверхность и перевода всех их бусин в нулевое положение. Далее можно привести несколько элементарных примеров, как считать на абакусе, выполнив сложение следующих чисел:
Для выполнения более сложных вычислений рекомендуется придерживаться того же алгоритма действий. В качестве наглядного примера можно привести число 372, для набора которого следует выставить в первом ряду две земные бусины, соответствующие единицам, во втором одну небесную и две земные (5+2=7), а в третьем три из земного, что равно трем сотням.
Сложение/вычитание и умножение/деление
Набив руку в наборе однозначных и многозначных чисел и научившись прибавлять и отнимать самые простые из них, можно смело переходить на следующий, более сложный уровень. И прежде всего речь идет о сложении и вычитании двухзначных чисел. К примеру, посчитать, сколько будет 27+43, на абакусе можно будет следующим образом:
Вычитание выполняется на основе аналогичного алгоритма, но только в обратную сторону, предполагающую отнимание десятых и добавление единиц, если таковые будут образовываться в остатке. Что касается умножения, то с ним также не должно возникнуть никаких трудностей, нужно только освоить таблицу умножения от 0 до 10.
Само решение выполняется в два этапа, которые предполагают разложение каждого числа на десятки и единицы с последующим их перемножением. Если же для расчета используются трехзначные и более сложные числа, следует придерживаться одного простого правила, согласно которому сначала перемножаются десятки, потом единицы с десятками и наоборот, а после сами единицы. Проще говоря, счет ведется от большего к меньшему с последовательным их набором на абакусе. По аналогии выполняется и деление, главное, не сбиться и соблюдать очередность выполняемых операций.
Античные счёты — слово из 4 букв в ответах на сканворды, кроссворды
Немного исторических фактов
Счёты являются тем устройством, с которого и начиналась вся история вычислительных предметов. Ещё много столетий назад счёты пользовались мировой популярностью.
Первое вычислительное устройство именовалось «счётной доской». Особенности его использования практически не отличались в различных странах, а вот для изготовления счётов использовались различные материалы.
Что касается времён Древней Руси, то вычисления на первых порах производились посредством использования специальных косточек, группируемых в виде своеобразных кучек. В последующем произошла трансформация счётов, которые обзавелись дощатым видом. Первые счёты были представлены деревянной рамой с верёвочками, на которые нанизывались ягодные косточки.
Именно от последнего внешнего вида вычислительных предметов и отталкивались специалисты, разработавшие те счёты, которые известны практически каждому человеку.
С момента появления эти приспособления стали необычайно популярны, ведь они активно применялись во всех местах, связанных с финансами и необходимостью проведения вычислительных операций. Во времена Советского Союза практически каждый человек владел навыками работы со счётами.
Русские счеты — история
Итак, что это такое? Русские счеты — это простейшее механичное устройство для осуществления вычислений. Это сложение, вычитание, деление и умножение. Имеют место две теории появления счет на Руси:
Как оно было на самом деле, история умалчивает. Но «дощаный» счет до середины XVII века (пока не победил) конкурировал с европейской системой счета на линованных досках типа абак, где он происходил при помощи камешков или специальных жетонов.
Как считать?
Образец – это старые деревянные счеты. Они имеют 12 поперечных проволочек-прутов (РР отделяет 8 верхних от 3 нижних) с десятью костяшками белого цвета, кроме двух черных посередине на 11 из них (на РР – 4 костяшки). Таким образом, русские счеты могут зафиксировать любое число до 10 миллионов. А если исключить РР, то до 10 миллиардов.
Итак, как считать на счетах? Откладывание чисел производится перемещением костяшек из правого в левое положение, а при наборе слева 10 косточек – они убираются в исходное положение. В следующем разряде в левое положение переводится всего лишь одна косточка. РР отделяет целые числа (сверху) от их соответственно десятых, сотых и тысячных долей и в расчетах участие не принимает (ранее использовался для учета «полушек», которая равнялась ½ «деньги» или ¼ копейки).
Счеты бухгалтерские
Они получили массовое распространение в XIX-XX веках, пока их не вытеснили ЭКВМ (электронно-клавишные вычислительные машины). Кстати, этого не смогли сделать арифмометры, которые считали намного быстрее, но работа на них требовала специальной и довольно сложной подготовки по овладению навыками работы на них, в отличии от счет, обучить работе на которых было в разы легче и быстрее.
Вообще-то искусство работы на бухгалтерских счетах и состоит в том, чтобы знать все способы достижения точного результата действий путем разложения общего на частные более легкие операции. Например, умножение на 25 заменяется умножением на 100 и двукратным последовательным делением результата на 2. Или, как умножение, так и деление на любую степень числа 2 производится последовательным соответствующим действием, число которых равно этой степени.
Как считать на счетах? Другой пример. Умножение на двузначное число из одинаковых цифр «АА» (11, 22 и так далее) заменяется умножением на «А» с переносом результата на разряд вверх (умножение на 10) и сложения этой суммы с предыдущей. От опыта и подготовки человека, работающего на счетах, метода его обучения и зависит скорость вычислений, а также применение им специальных приемов.
Сложение на счетах – самая легкая операция. Набирается первое число, потом к нему добавляются костяшки, обозначающее третье и так далее. Надо соблюдать только одно условие. При нехватке косточек для перемещения их в левый ряд – именно столько косточек необходимо оставить в этом ряду, после чего и переместить одну костяшку влево на верхнем пруте. Выполнение происходит сверху вниз (профессионалы могут и наоборот) и складываются только равные разряды (единицы с единицами, десятки с десятками и так далее).
Как выполняется вычитание на счетах? Помня, что счеты не работают с отрицательными числами, всегда надо иметь в виду, что вычитание производится из числа более крупного. А если надо сделать наоборот, то все-таки меньшее вычитается из большего, а знак запоминается или записывается. Вычитание на русских счетах производится сверху-вниз, то есть от высших разрядов к низшим. На соответствующей проволоке отбрасывается вправо необходимое число косточек и если их не хватает, то одна косточка переносится вправо в старшем разряде, а на данной проволочке все переносится влево и из них убирается вправо необходимое число.
Теперь про умножение на счетах. Древние счеты способствуют повышению скорости проведения действий по умножению, которая значительно превосходит скорость осуществления тех же действий на бумаге. На практике умножение – это многократное сложение искомого с самим собой в числовом выражении. Несколько советов:
Способы, упрощающие процесс умножения:
Как умножение заменяется многократным сложением, так и деление на счетах – это постоянное вычитание. Начинается все с верхнего разряда и идет вниз. Переносится направо число косточек, равных делителю (каждый раз, как это удается на самой верхней проволочке, переносится одна косточка налево) до тех пор, пока слева не окажется косточек меньше чем число, на которое производится деление (делитель).
Затем к процессу подключается нижеследующий разряд. И если в предыдущей проволочке остались косточки, то вычитается делитель уже из двузначного числа. Если нет, то, как в предыдущий раз. Если в низшем разряде вычитание пройдет без остатка косточек слева, то значит деление произведено без остатка. Если слева косточки остались, то в случае необязательного получения в итоге дробного числа – остаток игнорируется, а если обязательно его получение, то вычитание продолжается до нужной точности на прутьях ниже РР, с указанием дробного разделителя на бумаге. Аналогично производится деление на двухзначные, трехзначные (и т. д.) числа, только сначала вычитание идет из соответственно двух, трех и так далее высших разрядов.
Способы, упрощающие процесс деления:
На протяжении четверти тысячелетия популярности и практической необходимости счет неоднократно предпринимались (часто закончившиеся удачно), попытки усовершенствовать русские счеты. Остановимся только на одной из них. В 1828 г. генерал-майор Ф. М. Свободский представил в соответствующую инстанцию счетный прибор, который не только осуществлял привычные для русских счет действия, но достаточно быстро извлекал кубические корни, возводил числа в степень, вычислял сложные проценты и так далее. Достигалось это только методами сложения и вычитания с фиксацией промежуточных результатов на специальном поле счет. Однако скорость получения искомого результата так поразила комиссию, что она рекомендовала данный прибор к производству и введению специального курса в военных заведениях. Но до реального исполнения решения дело не дошло.
В настоящее время в России счеты применяются только в качестве музейного экспоната или семейной реликвии. Очень редко, если они наличествуют у кого-то в доме, могут использоваться подрастающим поколением для катания по полу, или старшими для массажа ног или спины. А зря! В современном Китае на «Суаньпань» учат учеников младших классов, так как считается, что освоивший такой способ счета ребенок развивается лучше и быстрее, не научившегося работать на этом древнем приспособлении.
Абак в разных регионах.
Абак впервые появился, возможно, в Древнем Вавилоне. 3 тыс. лет до н. э. Изначально являл собой доску, которая разграфлена на полосы или с углублениями. Счётные метки (косточки, камешки) передвигались по углублениям, линиям. В Египте в V в. до н. э. вместо углублений и линий стали применять палочки и проволоку с нанизанными камешками.
Абак применяли и народы Индии. Арабы с абаком знакомились у народов, подчинённых ими. В заглавиях большинства арабских руководств по арифметике есть слова, имеющие корень «пыль».
У индийцев, как и у восточных арабов абак скоро был вытеснен индийской нумерацией, однако он крепко держался у западных арабов, которые захватили в конце VIII века и Испанию. В X веке тут со счётом на абаке познакомился француз Герберт (940—1003), который написал об этом книгу (980—982) и пропагандировал через своих учеников и сам использование абака. При счёте на абаке вместо камешков использовались и жетоны с числовыми знаками, начертанными на них или римскими цифрами, или особенными числовыми знаками — апексами. По форме апексы Герберта близки к цифрам гобар западных арабов. Апексы Герберта и 27-колонный абак, предмет удивления современников (воссозданы в реставрированном виде по разным рукописям профессором Бубновым Н. М., профессором истории из Киевского университета, начало XX века). Усилиями многих учеников и последователей Герберта и при помощи его влияния, как папы римского (Сильвестра II, 999—1003) абак имеет широкое распространение в Европе. Следы данного распространения удержались, между прочим, в разных языках. Английский глагол обозначает графить — словом от такого же корня называют клетчатую материю, the cheque, или check — банковый чек, exchequer — казначейство. Последний термин проходит от того, что в банке расчёты производились на абаке, основание которого было в разграфлённой доске. Государственное английское казначейство называлось до последнего времени Палатой шахматной доски — по клетчатому сукну, которым покрывался стол заседаний. Клетчатая скатерть была абаком при вычислениях. Палата шахматной доски, которая возникла в XII веке была до 1873 года финансовым верховным управлением и высшим судом по финансовым вопросам.
В Европе абак использовался до XVIII века. В Средние века сторонники производства арифметических вычислений только с помощью абака — абацисты — в течение нескольких столетий проводили ожесточённую борьбу с алгоритмиками — приверженцами появившихся тогда методов алгоритмизации арифметических действий.
Ацтекские счёты появились примерно в X веке и изготавливались из кукурузных зёрен, которые нанизывались на струны, которые установлены в деревянной раме.
В Империи инков использовалось счётное устройство юпана (в паре с кипу), которая имела разновидности: геоюпана, арифметическая юпана и др. В юпане, судя по всему, применялась фибоначчиева система счисления.
В странах Востока имеется китайский аналог абака — японский и суаньпань — соробан. Конструкции аналогичны, применяют десятичную систему счисления, хотя японский вариант чуть экономичнее (в китайском, как и в русских счётах, применяются «лишние» косточки с точки зрения математики). Для японского и китайского абака есть скрупулёзно разработанный набор алгоритмов, которые позволяют механически (то есть не занимаясь добавочными вычислениями на бумаге или в уме) исполнять все четыре арифметических действия и извлекать даже кубические и квадратные корни.
Японский соробан активно применяется по сей день, невзирая на повсеместное распространение электронных калькуляторов. В Японии применение соробана — элемент школьной программы обучения в младших классах счёту. В Японии и странах, которые имеют большую японскую диаспору, Также счёт на соробане известен как своеобразный спорт или тип развлечения.
Русские счеты или десятичный абак, в которых применяется десятичная система счисления и возможность использовать четверти, десятые и сотые дробными долями возникли в России на рубеже XV — XVI веков и применялись активно в торговле до последнего десятилетия XX века. Счеты от классического абака отличаются увеличением разрядности всех числовых рядов и конструкцией. Ещё одна особенность русских счёт — выделенный специально разряд для счёта в четвертях. С момента своего появления счеты почти не менились.
С появлением электронных дешёвых калькуляторов счёты почти полностью вышли из применения. Ещё ранее, в начале 1980-х годов, обучение использованию счётами исключено из школьной программы в СССР.
Какие же инструменты помогали человечеству?
Древние люди делали зарубки на костях и камнях и носили эти палочки с собой, либо оставляли чёрточки на стенах жилищ. Одно из самых старинных устройств, которое не так уж далеко ушло от костей на полу пещеры — это, конечно, счёты. По сути они представляют собой те же кости (деревяшки, камушки), только нанизанные на спицы, которые закреплялись в раме.
Их близкий родственник — счётная доска абак, которая появилась в Вавилоне около пяти тысяч лет назад. Очевидно, что её появлению мы обязаны бурной вавилонской торговле. Если классические счёты, какими их знают в России, опираются на позиционную десятичную систему счисления, то вавилонский абак использовал шестидесятеричную. Такой оригинальный способ счёта происходит, как и большинство систем счисления, от пропорций человеческого тела — если говорить точнее, от числа фаланг пальцев на одной руке (не считая большого).
Вариации счётных досок были во всех древних культурах. В Японии они называются соробан, в Китае — суньпань. Римляне делали счёты из металла, передвигая костяшки в пазах металлической доски, а ацтеки — из кукурузных зёрен. Инки использовали для подсчёта зёрен «многоэтажное» устройство под названием юпана.
Как развивались счётные машины?
В общем виде счётная машина представляет собой устройство, работающее на зубчатых колёсах и цилиндрах, которое производит четыре основных математических действия. Записывающие счётные машины также могут автоматически фиксировать результаты на ленте. Принцип счёта основан на поразрядном сложении и сдвиге суммы частных произведений. Свои версии арифмометра создали Блез Паскаль, спроектировавший в 1646 году суммирующую машину «паскалина», и Готфрид Вильгельм Лейбниц: в его арифмометре была ручка, вращение которой ускоряло повторяющиеся операции.
Также следует упомянуть вычислительную машину, разработанную Чарльзом Бэббиджем в XIX столетии. Она могла производить вычисления с точностью до двадцатого знака, подходила для операций с логарифмами и тригонометрическими функциями. Программа для неё была составлена Адой Лавлейс, первой женщиной-программистом, да и вообще первым программистом в мире. Именно ей принадлежат термины «цикл» и «рабочая ячейка».
Электронный прорыв
Настоящий прорыв в развитии вычислительной техники случился в 60-х годах ХХ века.
В 1957 году японская компания Casio выпустила первый полностью электронный калькулятор 14-А. Событие было эпохальным, потому что открыло новую эру в мире счёта, но жизнь офисных работников и инженеров эта модель не изменила, ведь весил калькулятор целых 140 кг.
Первым компактным, а значит, массовым, калькулятором стал Anita, выпущенный английской компанией Bell в 1961 году. Он работал на газоразрядных лампах и был оснащён клавишами ввода числа и множителя. С тех пор функции калькуляторов становились всё более серьёзными, а сами калькуляторы — всё более лёгкими и умными.
Например, в 1965 году появился первый настольный электронный калькулятор со встроенной памятью Casio 001. Весил он всего 17 килограмм, что по тем временам для машины, способной запоминать операции, было вовсе не много, а два года спустя появился первый настольный программируемый калькулятор Casio AL-1000.
Однако пользователям калькуляторов было и этого мало, ведь счётное устройство куда удобнее держать в руке и носить с собой. Так появились калькуляторы Sharp и Canon, которые весили менее килограмма.
Жителям России особенно запомнились калькуляторы фирмы «Электроника»: шрифт, которым написано это слово, по сей день вызывает ностальгию у бывших советских граждан.
Вот ещё несколько эпохальных инноваций от японской марки Casio, которые существенно изменили представления о том, на что способны калькуляторы.
Появился карманный калькулятор Casio Mini, продажи которого побили все рекорды. А через некоторое время компания выпустила миниатюрную версию, Casio Mini Card, размером с кредитную карту.
Компания выпустила калькулятор FX-7000G — первый в мире программируемый графический калькулятор, доступный широкой публике, с матричным дисплеем, имеющем разрешение 96×64 пикселя. Эта модель может отображать как встроенные графики, так и построенные пользователем. В дополнение к режиму графического отображения калькулятор имеет функцию программирования на языке Бейсик.
Пять лет спустя на прилавках появился калькулятор Casio CFX-9800G, в котором впервые появилась возможность делать графики в разных цветах. По сути, был добавлен цветной дисплей. В отличие от современных экранов, он был трёхцветным и работал на отражённом свете. Это дало возможность рисовать каждый график своим цветом, что делало графические отображения функций куда более наглядными.
Casio выпускает устройство CASIO ClassPad 300 — первый калькулятор с большим сенсорным экраном. Модель имела систему компьютерной алгебры (CAS), которая позволяет производить преобразования выражений в аналитической (символьной) форме.
2004 год.появился калькулятор Casio FX-82ES с технологией Natural Display, позволяющий вводить выражения в естественном виде так, как они выглядят на бумаге. Например, вводить обыкновенные дроби, квадратные корни, экспоненты и логарифмы в виде, принятом в учебниках. В результате сокращается количество ошибок в вычислениях, время вычислений и повышается заинтересованность учеников
Модель калькулятора Casio fx-CG20 PRIZM явилась развитием первой модели, выпущенной в 2010 году. В отличие от предшественников она имела полноцветный экран высокого разрешения. Модель, несмотря на экран с подсветкой, не потеряла в энергоэффективности и способна месяцами работать на одном комплекте батарей.
Сейчас калькуляторы не только стали компактными и лёгкими, но и освоили массу функций, которые могут быть полезны всем, кому требуются точные и сложные расчёты. Сейчас существуют научные калькуляторы, которым под силу производить вычисления с дробями, считать векторы и матрицы, совершать метрические преобразования и решать уравнения, графические калькуляторы, позволяющие создавать таблицы и строить графики по картинке, а также финансовые калькуляторы, которые справляются с расчётом облигаций и другими нуждами финансиста.
На сегодняшний день флагманская графическая модель — калькулятор Casio FX-CG50 с цветным экраном высокого разрешения, возможностью строить 3D графики, режимом программирования, а также поддержкой векторных и матричных вычислений.