как строить графы отношений

Теория Графов. Часть 1 Введение и классификация графов

«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена

Введение

Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Схема Московского метро

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.

Отмечу, что число вершин обозначается буквой n:

Число рёбер обозначается буквой m:

Таким образом граф задается и обозначается парой V,E:

Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)

Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.

Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Нулевой граф

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.

Множество E задается парой неупорядоченных вершин множества V.

Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =

Граф будет выглядеть следующим образом:

Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.

Степень записывают, как:

Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:

Формула суммы степеней для G = V,E выглядит так:

То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!

А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:

Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?

Классификации графов

Первым признаком классификации является отсутствие или наличие ориентации у ребер.

Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Неориентированный граф

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Ориентированный граф

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Смешанный граф

Вторым признаком является отсутствие или наличие кратных ребер.

Мультиграф

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.

Заключение

В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.

Источник

Графы. Схема отношений

Описание разработки

Презентация состоит из 29 слайдов.

В данном проекте учащиеся изучают основные понятия: граф, ориентированный граф, неориентированный граф, схема отношений.

Эта работа также знакомит школьников с областью применения этой темы на других предметах.

В презентацию вставлена практическая работа, которая позволяет закрепить умения изображать графически схему отношений между объектами.

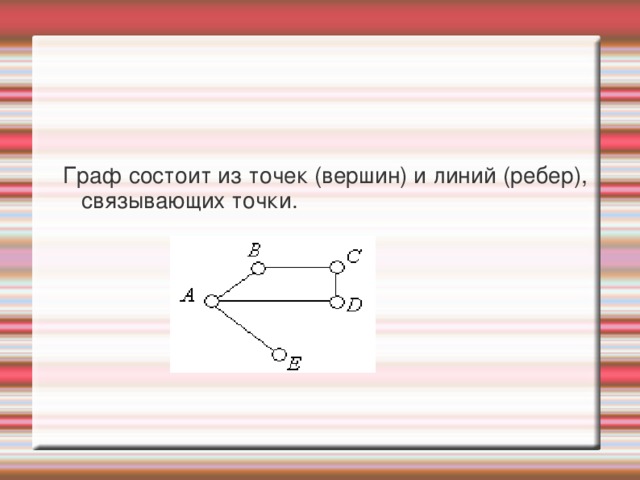
Граф состоит из точек (вершин) и линий (ребер), связывающих точки.

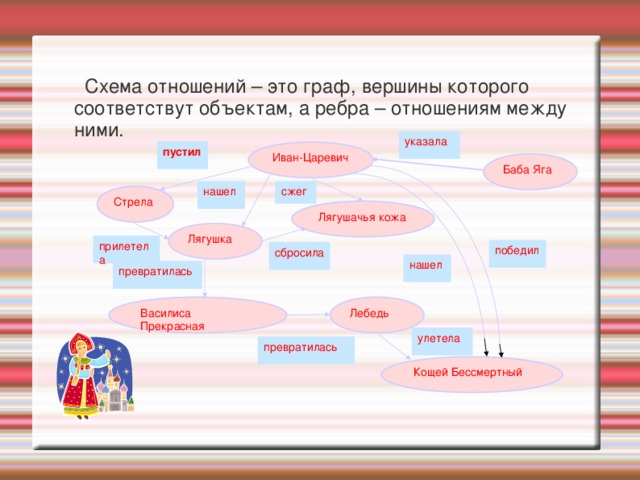
Схема отношений – это граф, вершины которого соответствут объектам, а ребра – отношениям между ними.

Некоторые отношения между объектами описываю с помощью направленных ребер. (Имена отношений изменятся, если два объекта в паре поменять местами.)

Первая работа о графах появилась в 1736 году в публикациях Петербургской академии наук. Она принадлежит Леонарду Эйлеру и связана с решением задачи о Кенигсбергских мостах.

Содержимое разработки

— Что мы понимаем под объектами?

— Можем ли мы города(людей, машины) рассматривать как объекты?

— Как вы понимаете выражение «отношения между объектами»?

Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехали за город, если всего было 10 рукопожатий?

Графы. Схема отношений.

Граф состоит из точек (вершин) и линий (ребер), связывающих точки.

Схема отношений – это граф, вершины которого соответствут объектам, а ребра – отношениям между ними.

Источник

Теория графов. Часть третья (Представление графа с помощью матриц смежности, инцидентности и списков смежности)

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).

Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).

Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.

Матрица смежности

Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.

Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.

Каждая ячейка матрицы равна либо 1, либо 0;

Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.

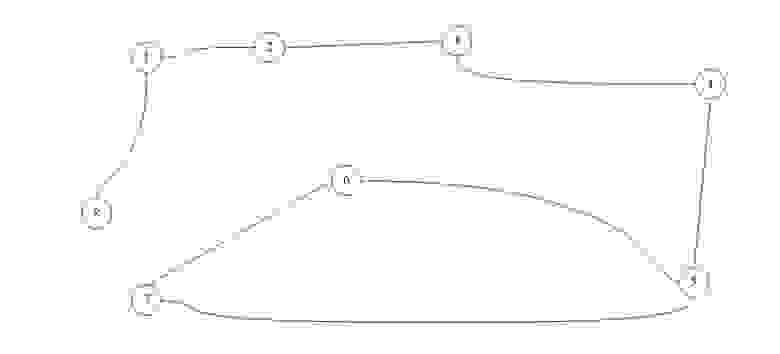
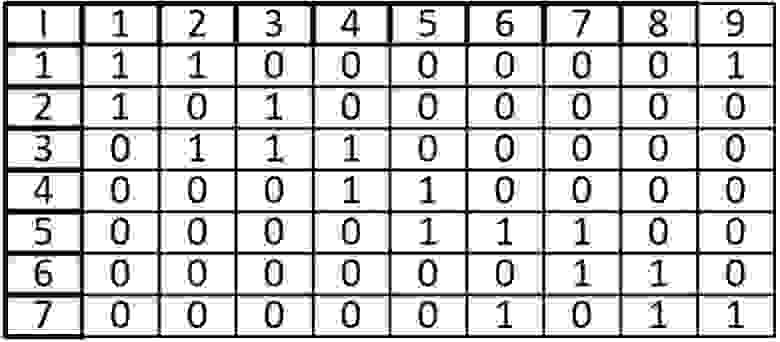
Для практического примера возьмем самый обыкновенный неориентированный граф:

А теперь представим его в виде матрицы:

Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.

С одной стороны объем памяти будет:

Но используя вышеописанный подход получается:

Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.

Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.

Если мы используем ориентированный граф, то кое-что меняется.

Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.

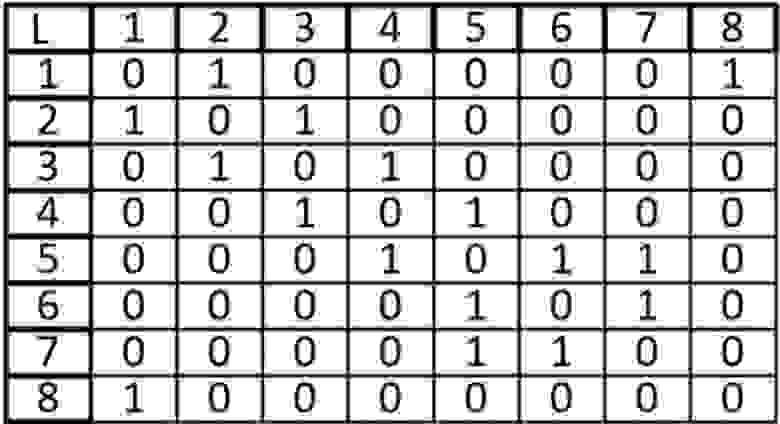
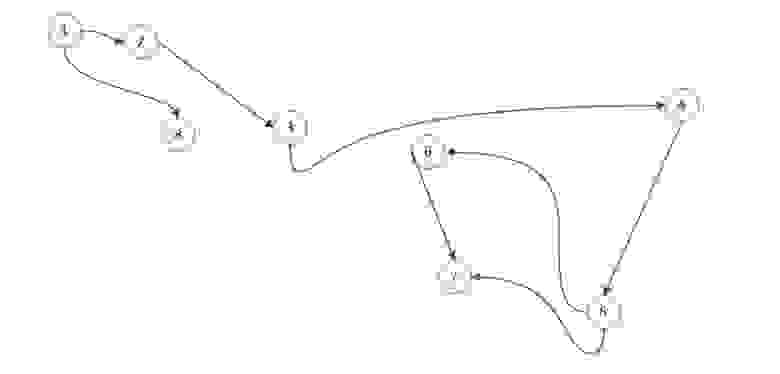
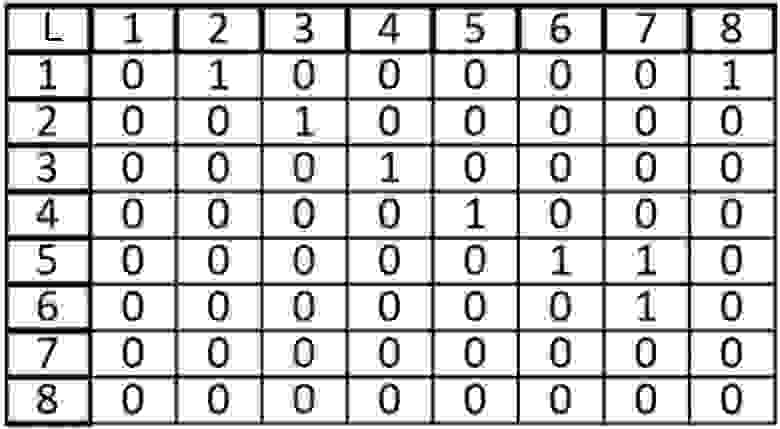
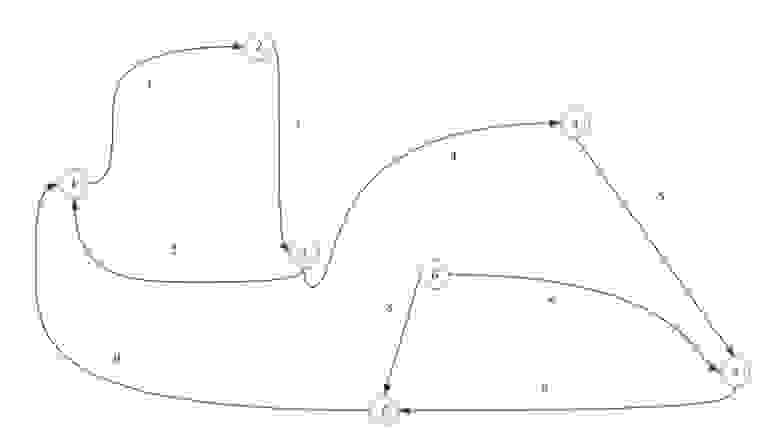
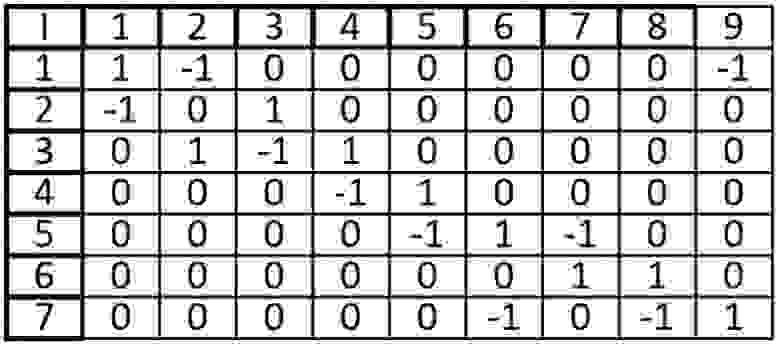
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.

Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.

Матрица инцидентности

Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.

Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.

Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.

Сразу же иллюстрируем данное правило:

Сумма элементов i-ой строки равна степени вершины.

Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.

Список смежности (инцидентности)

Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:

Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.

Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:

Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).

Сумма длин всех списков:

Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.

К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.

Взвешенность графа

К примеру, возьмем граф с весами на ребрах:

И сделаем матрицу смежности:

В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.

Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.

Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.

Если заметили ошибку или есть предложения пишите в комментарии.

Источник

Тема: Отношения

Цель: Дать понятие отношения между элементами одного множества. Показать способы задания отношения между элементами одного множества, рассмотреть свойства отношений.

Понятие отношения. Способы задания отношений. Свойства отношений. Отношение эквивалентности. Отношение порядка.

1. Понятие отношения

На рисунке 1 изображены сестры Анна Ивановна и Вера Ивановна с сыновьями Петей и Юрой. Между этими людьми существуют различные родственные отношения. Рассмотрим некоторые из них.

а) Петя – сын Анны Ивановны. В этом же отношении «быть сыном» находится Юра с Верой Ивановной. В отношении «быть сыном» не находятся Вера Ивановна и Анна Ивановна.

Рис.1 Выпишем все пары элементов, находящихся в отношении «быть сыном». Таких пар две: (Петя; Анна Ивановна) и (Юра; Вера Ивановна).

Эти пары можно представить с помощью особого чертежа, состоящего из точек, соединенных стрелками. Такие чертежи называются графами. Такой граф называют графом отношения «быть сыном» (рис. 2).

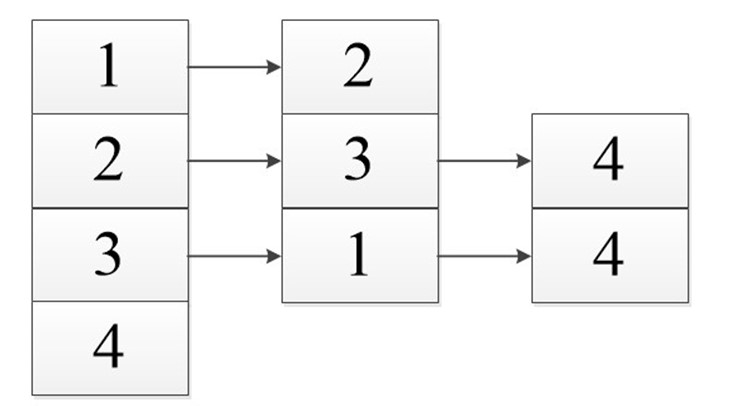
б) Анна Ивановна – тетя Юры. В этом же отношении «быть тетей» находятся еще лишь Вера Ивановна и Петя. Граф отношения «быть тетей» показан на рисунке 3.

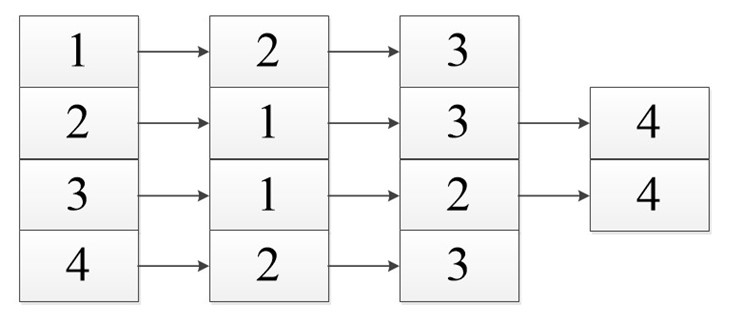
в) В отношении «быть сестрой или матерью» находятся элементы четырех пар: (А. И.; В. И), (В. И.;А. И.), (А. И.; П.), (В. И.; Ю.), граф этого отношения представлен на рисунке 4.

Рис. 2 Рис.3 Рис.4

Таким же образом можно представить графы отношений «быть двоюродным братом», «быть племянником» и др.

Из курса школьной математики известны многочисленные примеры отношений:

— между числами: «равно», «неравно», «меньше», «больше», «кратно», «следует за…», «делится на…» и т. д.;

— между точками прямой: «предшествует», «следует за» и т. д.;

— между прямыми: «параллельны», «пересекаются», «перпендикулярны»;

— между плоскостями: «параллельны», «пересекаются», «перпендикулярны»;

— между геометрическими фигурами: «равно», «подобно», и др.

Таким образом, в математике изучают не только сами объекты (числа, фигуры, величины), но и связи между ними, т. е. отношения между этими объектами.

Чаще всего в математике рассматривают отношения между двумя объектами, их называют бинарными; отношения между тремя элементами – тернарными; отношения между n элементами – n-арными.

Наша задача научиться устанавливать, что общего между отношениями, каким образом можно классифицировать такое огромное количество самых разнообразных отношений.

Значение этого материала нужно учителю начальных классов и воспитателю дошкольного учреждения для того, чтобы, изучая конкретные отношения в начальной математике понимать их сущность, взаимосвязи, роль в усвоении тех или иных понятий.

Рассмотрим множество чисел Х=<3,4,5,6,8>. Между числами этого множества можно установить такие отношения как:

— «больше»: 4>3, 5>3, 6>3, 8>3, 5>4, 6>4, 8>4, 6>5, 8>5, 8>6;

— «больше на 1»: «4 больше 3 на 1», «5 больше 4 на 1», «6 больше 5 на 1»;

— «меньше в 2 раза»: «3 меньше 6 в 2 раза», «4 меньше 8 в 2 раза».

Итак, связь между элементами одного и того же множества называется отношением между элементами этого множества.

Обратим внимание на следующее: рассматривая то или иное неравенство, мы каждый раз оперировали упорядоченными парами, образованными из чисел данного множества. Поэтому полученные неравенства можно записать иначе, в виде упорядоченных пар. Рассмотрим на примере отношения «больше»:

Известно, что упорядоченные пары – это элементы декартова произведения множеств или его подмножеств. Поэтому об отношении «больше» заданном на множестве Х можно сказать, что оно является подмножеством множества .

Вместо того чтобы говорить, что отношение определяется множеством пар, в математике само это множество пар называют, отношением между элементами множества Х. Отношения обозначаются прописными буквами латинского алфавита: P, Q, R, S и др.

Определение. Отношением между элементами множества Х или отношением на множестве Х называется всякое подмножество декартова произведения Х´Х.

Как было сказано выше, отношение можно показать наглядно с помощью графов.

Рассмотрим отношения «больше» между элементами множества Х=<2;4;6;8;12>.

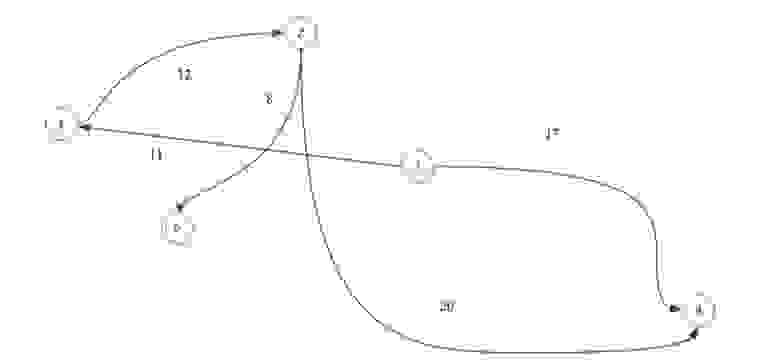
Для того чтобы построить граф этого отношения надо элементы данного множества изобразить точками и соединить стрелками те точки, которые изображают числа, находящиеся в отношении «больше». Поскольку 4>2, то проводим стрелку от 4 к 2; т. к. 6>4, то проводим стрелку от 6 к 4 и т. д., пока не переберем все пары чисел, связанных заданным отношением. В результате получаем граф отношения «больше» для элементов множества Х= <2;4;6;8;12>(рис.5). Рис.5

Рассмотрим теперь на этом множестве отношение «кратно» и построим граф.

Аналогично предыдущему случаю изобразим элементы множества Х точками и соединим стрелками те, которые изображают числа, находящиеся в отношении «кратно»: 12 кратно 2, 12 кратно 4 и т. д. Так как любое число из множества Х кратно самому себе, то граф данного отношения будет иметь стрелки, начало и конец которых совпадут. Такие стрелки на графе называют петлями (рис.6). Рис. 6

Вопросы и задания по теме:

1. Дайте понятие отношения на множестве. Приведите примеры отношений на множестве.

2. Приведите примеры отношений, существующих между:

а) натуральными числами;

б) прямыми на плоскости;

3.

Установите, какой из графов, приведенных на рисунке 7, является графом отношения «х делится на у», заданного на множестве Х=<5;10;20;30;40>. Ответ поясните. Рис. 7

4. Какое из следующих множеств является отношением между элементами множества А=<0;3;6;9;12>:

2. Способы задания отношений

1. Отношение R на множестве Х можно задать, перечислив все пары элементов, взятых из множестве Х и связанных этим отношением. Формы записи при этом могут быть различными:

2. Чаще отношение R на множестве Х задают, указав характеристическое свойство всех пар элементов, находящихся в отношении R:

а) словесное: «больше», «кратно», «меньше в 2 раза», «— простое число» и т. д.

б) неравенством: или равенством: .

Вопросы и задания по теме:

1. Перечислите способы задания отношений. Приведите примеры.

2. Задайте разными способами отношение «быть меньше» на множестве Х=<1, 3, 5, 7>.

3. Свойства отношений

Было установлено, что в математике изучают разнообразные отношения между двумя объектами. Каждое из них рассматривается на некотором множестве Х и представляет собой множество пар. Рис.9

параллельности равенства перпендикулярности «длиннее»

1. Рассмотрим графы отношений параллельности и равенства. Они имеют петли, которые говорят о том, что, какой бы отрезок из множества Х мы ни взяли, о нем можно сказать, что он параллелен самому себе или что он равен самому себе.

Про отношения параллельности и равенства говорят, что они обладают свойством рефлективности или просто, что они рефлексивны.

Определение. Отношение R на множестве Х называется рефлексивным, если о любом элементе множества Х можно сказать, что он находится в отношении R с самим собой.

рефлексивно на для любого

Таким образом, если отношение рефлексивно, то в каждой вершине графа имеется петля.

2. Рассмотрим теперь графы отношений параллельности, перпендикулярности и равенства отрезков. Их особенность в том, что если одна стрелка, соединяющая пару элементов, то обязательно есть и другая, соединяющая те же элементы, но идущая в противоположном направлении. Эти стрелки говорят о том, что:

а). если первый отрезок параллелен второму отрезку, то и второй отрезок параллелен первому;

б). если первый отрезок перпендикулярен второму отрезку, то и второй отрезок перпендикулярен первому;

в). если первый отрезок равен второму, то и второй отрезок равен первому.

Про отношения параллельности, перпендикулярности и равенства говорят, что они обладают свойством симметричности или, просто, симметричны.

Определение. Отношение R на множестве Х называется симметричным, если из того, что элемент х находится в отношении R с элементом у, следует, что и элемент у находится в отношении R с элементом х.

симметрично на .

Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к х.

Существуют отношения, которые свойством симметричности не обладает. Таким, например, является отношение «длиннее» для отрезков.

3. Рассмотрим граф отношения «длиннее». Его особенностью является, то, что если стрелка соединяет две вершины, то она только одна. Про отношение «длиннее» говорят, что оно обладает свойством антисимметричности или, просто, антисимметрично.

Определение. Отношение R на множестве Х называется антисимметричным, если для различных элементов х и у из множества Х из того, что элемент х находится в отношении R с элементом у, следует, что элемент у в отношении R с элементом х не находится.

антисимметрично на и .

Граф антисимметричного отношения обладает особенностью: если две вершины графа соединены стрелкой, то эта стрелка только одна.

4. Не следует думать, что все отношения делятся на симметричные и антисимметричные. Встречаются отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности. Обратим внимание еще на одну особенность графов отношений параллельности, равенства и «длиннее» (эта особенность не сразу заметна): если стрелка идет от первого элемента ко второму и от второго – к третьему, то обязательно есть стрелка, идущая от первого элемента к третьему. Эта особенность графов отражает свойство данных отношений, называемое свойством транзитивности.

Определение. Отношение R на множестве Х называется транзитивным, если из того, что элемент х находится в отношении R с элементом у и элемент у находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z.

транзитивно на и .

Граф транзитивного отношения с каждой парой стрелок, идущих от х к у и от у к z, содержит и стрелку, идущую от х к z.

Вопросы и задания по теме:

1. Сформулируйте свойство рефлективности. Приведите пример отношений, обладающих свойством рефлективности.

Рис.11

Рис.12

2. На рисунке11 изображены графы трех отношений. Какие из этих отношений рефлексивны?

3. Сформулируйте свойство симметричности. Приведите пример отношений, обладающих свойством симметричности.

4. На рисунке12 изображены графы трех отношений. Какие из этих отношений симметричны?

5. Сформулируйте свойство антисимметричности. Приведите пример отношений, обладающих свойством антисимметричности.

6. На рисунке 13 изображены графы четырех отношений. Какие из этих отношений антисимметричны?

7. Сформулируйте свойство транзитивности. Приведите пример отношений, обладающих свойством транзитивности.

8. На рисунке 14 изображены графы четырех отношений. Какие из этих отношений транзитивны?

9.

Установите, какими свойствами обладают отношения, графы которых представлены на рисунке15.

Рис.15 а) Рис. 15 б) Рис. 15 в)

10. Обладает ли отношение Р на множестве <0;1;2;3;4>свойством транзитивности, если Р=<(0;1),(1;2),(2;3),(3;4)>?

Рассмотрим на множестве дробей , отношение: «равенства».

Построим граф этого отношения (рис.16 ) и определим его свойства. Это отношение:

— рефлексивно, т. к. всякая дробь равна сама себе; Рис. 16

— симметрично, т. к. из того, что дробь х равна дроби y, следует, что дробь y равна дроби x;

— транзитивно, т. к. из того, что дробь x равна дроби y и дробь y равна дроби z, следует, что дробь x равна дроби z.

Таким образом, отношение равенства дробей рефлексивно, симметрично и транзитивно. Говорят, что такое отношение является отношением эквивалентности.

Определение. Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойствами рефлексивности, симметричности и транзитивности.

Почему в математике выделили этот вид отношений? Посмотрим на граф отношения равенства дробей. Видим, что множество, на котором задано отношение, разбивается на несколько подмножеств. Так, на графе отношения равенства дробей выделяются три подмножества: , , . Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т. е. имеем разбиение множества Х на попарно непересекающиеся подмножества. Это не случайно.

Теорема. Если на множестве Х задано отношение эквивалентности, оно разбивает это множество на попарно непересекающиеся подмножества (классы эквивалентности).

Верно и обратное утверждение: если какое-либо отношение, заданное на множестве Х, определило разбиение этого множества на классы, то это отношение есть отношением эквивалентности.

Слово «порядок» мы употребляем часто как в обыденной жизни, так и на занятиях по математике. Мы говорим о порядке поступления в учебное заведение, о порядке слов в предложении; на уроках математике обсуждаем порядок выполнения действий, порядок записи решения уравнения, задачи и т. д.

Что же такое порядок? Рассмотрим несколько примеров:

1) Чтобы установить порядок в множестве учащихся класса, достаточно выстроить их по росту. Таким образом, на данном множестве задается отношение «быть выше». Это отношение антисимметрично и транзитивно.

2) Множество класса можно упорядочить и по возрасту, т. е. задав отношение «быть старше». Заметим, что это отношение также антисимметрично и транзитивно.

3) Всем известен порядок следования букв в русском алфавите. Его обеспечивает отношение «следует за», обладающее свойствами антисимметричности и транзитивности.

Определение. Отношение R на множестве Х называется отношением порядка, если оно транзитивно и антисимметрично.

Определение. Множество Х с заданным на нем отношением порядка называется упорядоченным множеством.

Множество Х= <2, 8, 12, 32>можно упорядочить при помощи отношения «меньше» рис. 17а), а можно это сделать при помощи отношения «кратности» рис.17б). но, являясь отношениями порядка, отношения «меньше» и «кратно» упорядочивает множество натуральных чисел по-разному.

Не следует думать, что все отношения делятся на отношения эквивалентности и отношения порядка. Существует огромное число отношений, не являющихся ни отношением порядка, ни отношением эквивалентности.

Уже в дошкольном возрасте дети знакомятся с отношениями «больше» и «меньше» для натуральных чисел. Затем появляются отношения «длиннее» и «короче» для отрезков и т. д. При помощи этих отношений устанавливается порядок в множестве чисел и в множестве отрезков.

Источник