как в маткаде перевести комплексное число в показательную форму

Как в маткаде перевести комплексное число в показательную форму

Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.

Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить 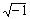, Mathcad вернёт i.

Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.

При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.

Специальные операции над комплексными числами

В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:

Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.

Рисунок 2: Комплексные числа в Mathcad.

При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.

Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.

Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.

Рисунок 3: Нахождение вещественных корней n—ой степени из отрицательного числа.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Как в маткаде перевести комплексное число в показательную форму

Глава 3. Работа с векторами и матрицами

MathCAD с одинаковым успехом вычисляет выражения с действительными и комплексными числами.

Комплексные числа можно записывать в любой принятой в математике форме:

– обычной (в виде суммы действительной и мнимой частей числа) – с=а+ b · i ;

– в тригонометрической форме – c = A ·( sin ( φ )+ i · cos (φ));

Для ввода мнимой единицы надо набрать с клавиатуры 1 i или 1 j и ввести число. При выведении курсора из области числа символ 1 исчезает, остается комплексное число в привычном виде (рис. 3.23 ).

расчет токов в цепи по уравнениям Кирхгофа ORIGIN:=1

Рис. 3. 23 Ввод комплексных чисел

Расчет напряжений по закону Ома

без оператора векторизации выведено скалярное произведение векторов

это не аргумент функции—без вывод комплексно-сопряженных чисел

оператора векторизации не обойтись

Рис. 3. 24 Расчеты с векторами комплексных чисел

Модуль комплексного числа вычисляется оператором || вводимым с панелей Calculator (Калькулятор) или Matrix (Матрица). Тот же оператор позволяет вычислить модуль вектора или определитель матрицы.

Аргумент комплексного числа вычисляется по формуле встроенной функцией arg ( A ), которая выдает угол поворота вектора в системе координат Re – Im (рис. 3.25 ).

модуль комплексного числа. необходим оператор векторизации

аргумент комплексного числа

угол в радианах угол в градусах

Рис. 3. 25 Вычисление модуля и аргумента комплексных чисел

Источник

Перевод комплексного числа в маткаде в показательную форму

Перевод комплексного числа в маткаде в показательную форму

Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.

Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить 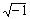, Mathcad вернёт i.

Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.

При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.

Специальные операции над комплексными числами

В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:

Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.

Рисунок 2: Комплексные числа в Mathcad.

При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.

Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.

Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.

Рисунок 3: Нахождение вещественных корней n—ой степени из отрицательного числа.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Работа с комплексными числами в Mathcad

Mathcad поддерживает вычисления с комплексными числами. Согласно математического определения, любое комплексное число можно записать в виде a+bi,где a – действительная часть, b – мнимая часть, i – мнимая единица. В некоторых случаях мнимую единицу принято обозначать как j, для Mathcad это – равнозначные понятия.

Некоторые операции над действительными числами, например, квадратный корень из отрицательного числа, по умолчанию возвращают результат в виде комплексного числа. Поскольку действительные числа есть подмножество комплексных, никаких переключений не требуется.

Поскольку во многих расчетах часто фигурируют переменные i или j (например, при организации суммирования по i), которые не являются мнимой единицей, для ее записи используются специальные сочетания. В частности, отдельно стоящая мнимая единица вводится как 1i или 1j (без пробела и каких-либо разделительных символов). Если мнимая единица вводится со своим числовым множителем в составе мнимой части комплексного числа, следует вводить число и букву iили j подряд, без пробела и знака «умножить». Однако, если в качестве множителя мнимой части выступает переменная, после ее имени необходимо ввести знак умножитьи мнимую единицу в виде 1iили 1j.

Другим способом ввода мнимой единицы (только в виде i) является кнопка на панели инструментов «Калькулятор».

Комплексные числа, наравне с действительными, могут входить в состав массивов (векторов и матриц), быть аргументами функций, участвовать в других вычислениях.

Если комплексное число записано в форме a+bi, то у него имеется так называемое сопряженное комплексное число вида a-bi. Для быстрого нахождения комплексного сопряженного числа служит оператор, вводимый при помощи сочетания клавиш Shift+’ (рядом с клавишей Enter).

MathCAD — это просто! Часть 19. Немного о работе с комплексными числами

Комплексные числа — одна из важнейших математических абстракций, очень часто используемая в реальных расчетах инженерами, физиками, электронщиками и другими специалистами. Само собой, настолько важная часть математики, как работа с комплексными числами, не могла остаться вне поля зрения разработчиков MathCAD’а. Сегодня мы с вами как раз и поговорим о том, как можно работать в MathCAD’е с ними — вы сможете самостоятельно убедиться в том, что это, в общем-то, не представляет каких-либо особых сложностей для пользователя этого мощнейшего математического пакета.

Комплексные числа в MathCAD: основы

Весь тот небольшой экскурс в работу с комплексными числами, который я привел выше, нужен только для того, чтобы напомнить (или, если кто-то не знал этого, то разъяснить), что же такое комплексные числа, и как именно с ними нужно работать. При работе в MathCAD’е, само собой, вам не понадобится собственноручно вычислять модуль и аргумент комплексного числа, не надо будет самостоятельно высчитывать степень экспоненты при перемножении комплексных чисел и даже не понадобится самому складывать действительную часть с действительной, а мнимую — с мнимой. Все за вас сделает этот мощный математический пакет. То есть, конечно, не все, а только черновую, вычислительную работу — постановка задачи и интерпретация результатов вычислений все равно останется за вами. Хорошая новость состоит в том, что для работы с комплексными числами не нужно как-то по- особенному настраивать среду MathCAD или применять какие-то новые арифметические операторы. Среда точно так же работает с комплексными числами, как и с действительными. Простой пример — сложение комплексных чисел. Попробуйте сложить два комплексных числа — например, 1+2i и 7-15i. Здесь, правда, стоит отдельно сказать пару слов относительно ввода в MathCAD’е мнимой единицы. Дело в том, что, если вы просто напишете ее как i, нажав на клавиатуре соответствующую клавишу, то система MathCAD посчитает, что вы ввели имя какой-либо переменной. Поэтому можно либо воспользоваться панелью инструментов Calculator (см. иллюстрацию, на которой нужная кнопка обведена кружком), либо вводить с клавиатуры комбинацию 1i.

После того, как вы попробуете складывать комплексные числа, можно попробовать их перемножать, чтобы убедиться в том, что MathCAD умеет делать и это. Можете попробовать возводить комплексные числа в какую-либо степень, а также любым другим образом поиздеваться над ними. Как и следовало ожидать, MathCAD с легкостью справляется с подобными заданиями. Поэтому вы можете работать с комплексными числами фактически точно так же, как и с действительными.

Комплексные числа в MathCAD: подробности и тонкости

Впрочем, конечно же, есть и некоторые тонкие моменты, связанные с отличиями в работе с комплексными и действительными числами. Самое главное из подобного рода отличий состоит, собственно говоря, в том, что операция извлечения корня с ними работает не совсем так, как надо — как, впрочем, и операция возведения в дробную степень, хотя для действительных чисел данные операции и абсолютно корректны. Дело в том, что на множестве комплексных чисел мы рассматриваем корень p n-й степени из числа z как множество решений уравнения pn = z. Если вы попробуете решить это уравнение с помощью оператора solve (хоть о нем мы говорили уже достаточно давно — думаю, вы еще не до конца забыли, как им пользоваться), то увидите, что для n-й степени это уравнение, согласно основной теореме алгебры, будет иметь ровно n решений. Если же для вычисления корня комплексного числа вы воспользуетесь операторами извлечения корня или возведения комплексного числа в дробную степень, то увидите, что подобные вычисления дадут вам только один корень из всех возможных, что не вполне корректно. Впрочем, в ряде практических задач вам будет нужен только один корень, но все равно его лучше получать с помощью solve, а затем уже выбирать среди результатов.

Ну, и напоследок такой вопрос: а как лучше обозначать мнимую единицу? Дело в том, что в литературе встречается два варианта ее обозначения: i и j. Первый более характерен для советских и постсоветских источников, второй — для зарубежных. Вполне может случиться так, что вам потребуется в вашем проекте использовать второе, а не первое, которое используется в MathCAD по умолчанию. Конечно же, эта мощная математическая среда позволяет нам изменить обозначение мнимой единицы на то, которое будет для нас наиболее удобным. Для того, чтобы поменять обозначение, нужно в меню Format выбрать пункт Result, а в появившемся окне на вкладке Display Options заменить параметр Imaginary Value. Вариантов этого параметра, конечно, не много — собственно, их всего два: либо i, либо j. Но больше вариантов, собственно говоря, и нету.

Итак, мы с вами познакомились с комплексными числами, а также с тем, как именно работать с ними в MathCAD’е. Вы смогли сами убедиться, что это совсем несложно, хотя, конечно, некоторые вычисления и имеют свои тонкости. Но тонкости есть везде, и главное — быть заранее готовым к тому, что есть немалый шанс с ними столкнуться. Поэтому, если вы внимательно читаете статьи серии «MathCAD — это просто», то будете хорошо подготовлены к встречам с различными неожиданностями в среде MathCAD. Успехов вам в работе с этим мощным математическим пакетом и интересных вычислений!

Компьютерная газета. Статья была опубликована в номере 33 за 2008 год в рубрике soft

Источник

Здравствуйте. Вот уже не первый час ночи пытаюсь заставить его перевести число из комплексного(z=x+jy) в показательную(e^jФ). И справку перекурил уже и гугл, везде только об обратной операции сказано, которая выполняется просто по нажатию знака равно.
Или я просто уже не могу сообразить и утро вечера мудренее.
Выручайте.
Ах, да. Использую Prime 2.0, но есть и 15

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Перевести комплексное число из алгебраической в показательную форму
Как в маткаде перевести комплексное число с алгебраической в показательную форму? Заранее спасибо.

Комплексное число из алгебраической в показательную и тригонометрическую
Добрый день, осваиваю Mathcad, дошел до комплексных чисел. Имеются два числа, первое A=3.6-8i, а.

Есть ли разница как переводить из алгебраической формы в показательную?
Есть такая функция \frac<1> <1-jw>Мы можем перевести знаменатель из алгебраической формы в.

Вывод формулы, по которой комплексное число из алгебраической формы представляется в показательной
Помогите вывести формулу, по которой мы комплексное число Z = a+bi из алгебраической формы.

Комплексное число. Перевод в показательную форму.
Подскажите пожалуйста, при помощи каких манипуляций в Маткаде сделать перевод из алгебраической.

Класс: Комплексное число в алгебраической форме a=x+y*i
Класс: Комплексное число в алгебраической форме a=x+y*i Члены класса: Действительная x и мнимая.

Источник