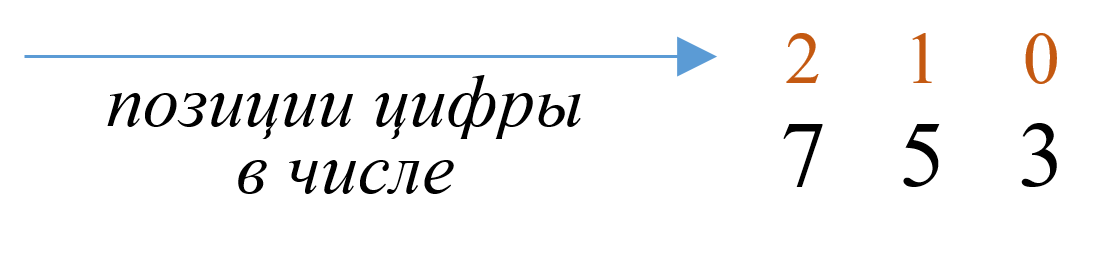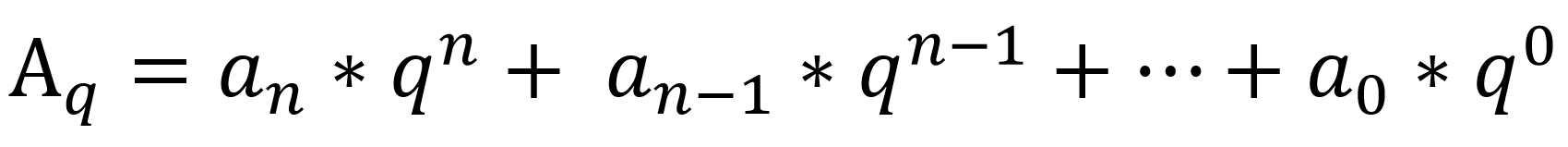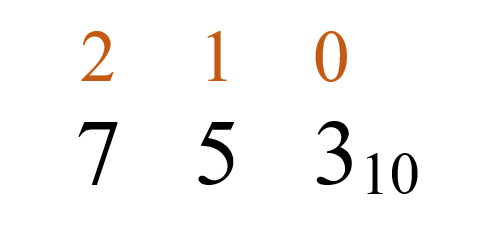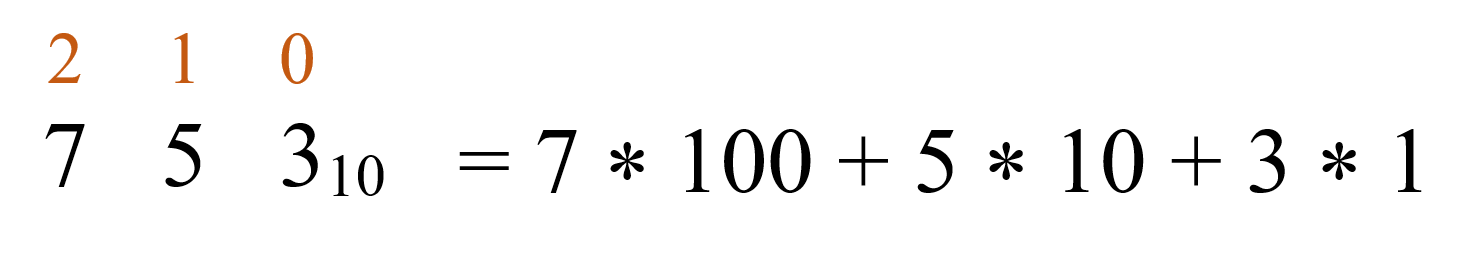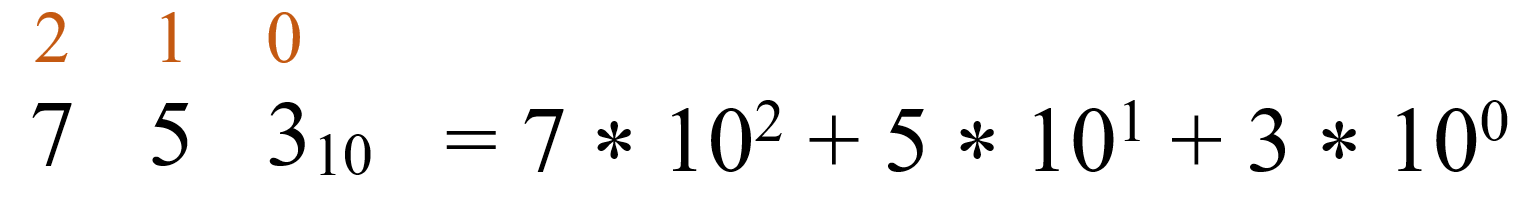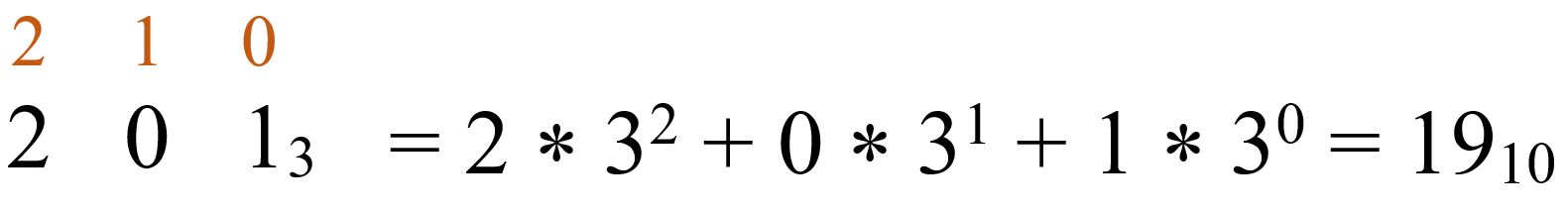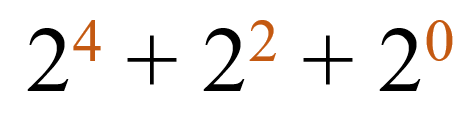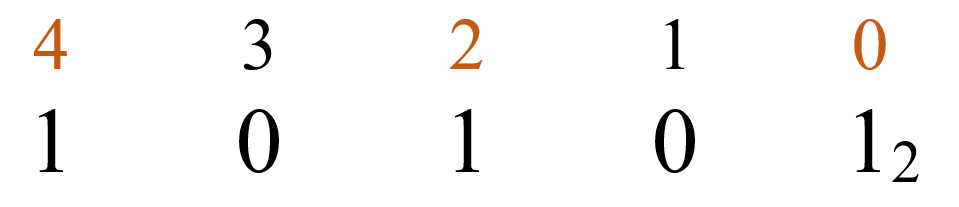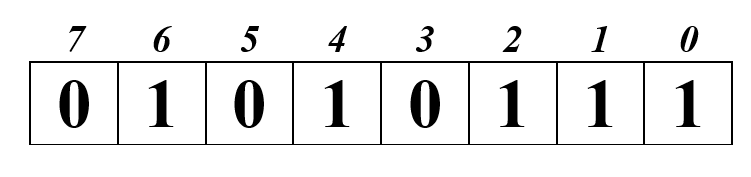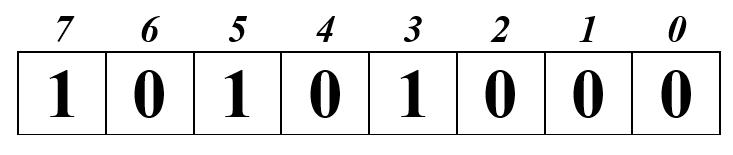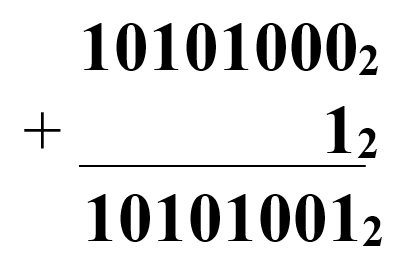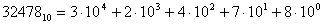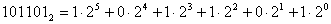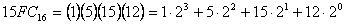как записать двоичное число в развернутой форме
Как записать двоичное число в развернутой форме
Любой вид информации можно представить в виде чисел. Кодирование информации с помощью чисел осуществляется по определённым правилам. Для понимания этих правил, разберём логику образования любого числа.
| Система счисления – это правила записи чисел с помощью знаков – цифр и операций над ними.
Любое число, в данной системе счисления, образуется путём повторения одинаковых элементов (палочка, камешек, ракушка и т.д.).
Данная система счисления позволяет записывать только натуральные числа и запись «большого» числа получается очень громоздкой.
В дальнейшем, у человечества возникла необходимость производить серьёзные подсчёты. Для этого были придуманы непозиционные системы счисления.
| Непозиционная система счисления – это система счисления, в которой цифра не изменяет своего значения, от изменения позиции в числе.
Египетская система счисления 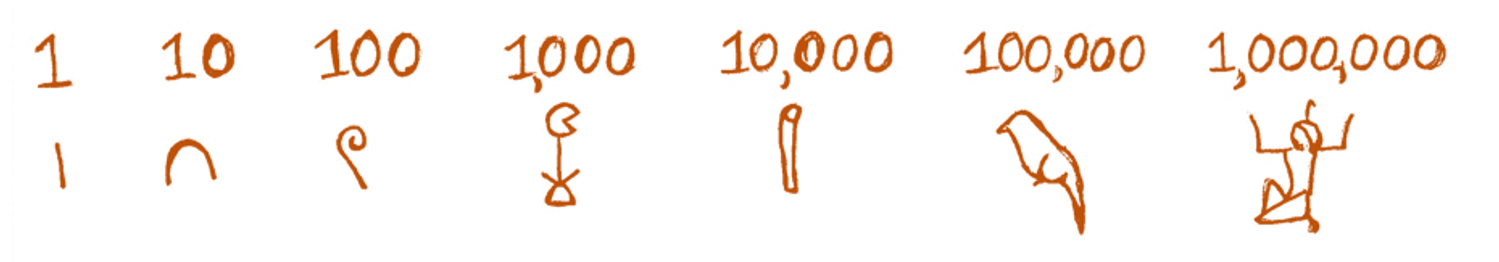
Кириллическая система счисления 
Римская система счисления 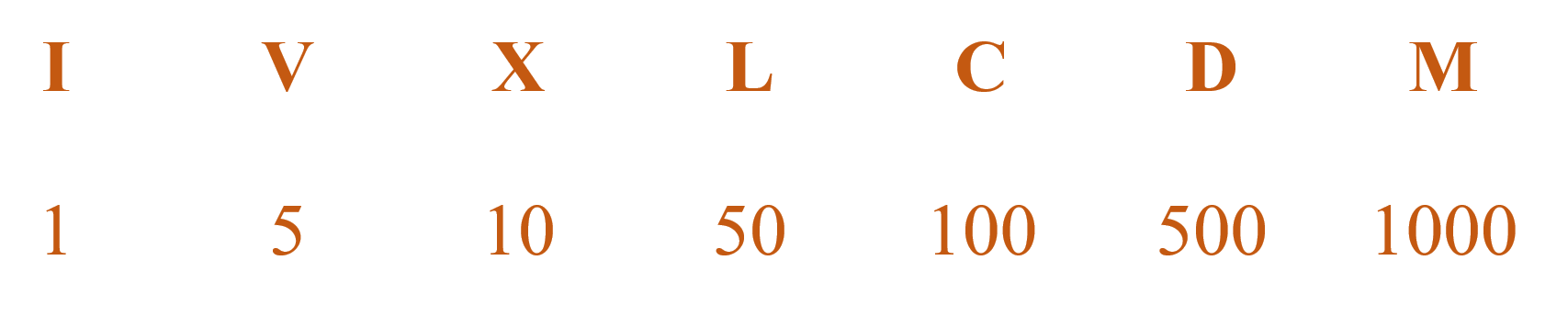
| Позиционная система счисления – это система счисления, в которой цифра изменяет своё значения, при изменении позиции в числе.
Вспомним, что любое число в десятичной (арабской) системе счисления можно разложить на разряды. Например, в числе 753 цифра 7 обозначает сотни (700), цифра 5 – десятки (50), цифра 3 – единицы. Таким образом, число можно представить, как:
753 = 7 * 100 + 5 * 10 + 3 * 1
| Алфавит системы счисления – совокупность всех её цифр.
| Основание системы счисления – указывает на количество цифр в данной системе счисления.
Алфавит десятичной системы счисления состоит из цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Следовательно, основанием данной системы счисления является 10.
Тогда, любое число будем записывать по правилу, с указанием основания данной системы счисления:
Число читается, как «семьсот пятьдесят три по основанию десять» или «семьсот пятьдесят три в десятичной системе счисления».
| Разряд – это позиция цифры в числе (нумерация в целых числах производится с права налево, начиная с нуля).
Укажем разряд каждой цифры в числе 753:
Развёрнутая форма представления чисел
В результате разбиения числа на разряды, любое такое число можно представить в развёрнутой форме.
Формула развёрнутой формы представления чисел:
q – основание системы счисления;
a – цифра данного числа;
n – число разрядов в числе.
Представим число 75310 в развёрнутой форме.
1) Определим позиции каждой цифры в числе:
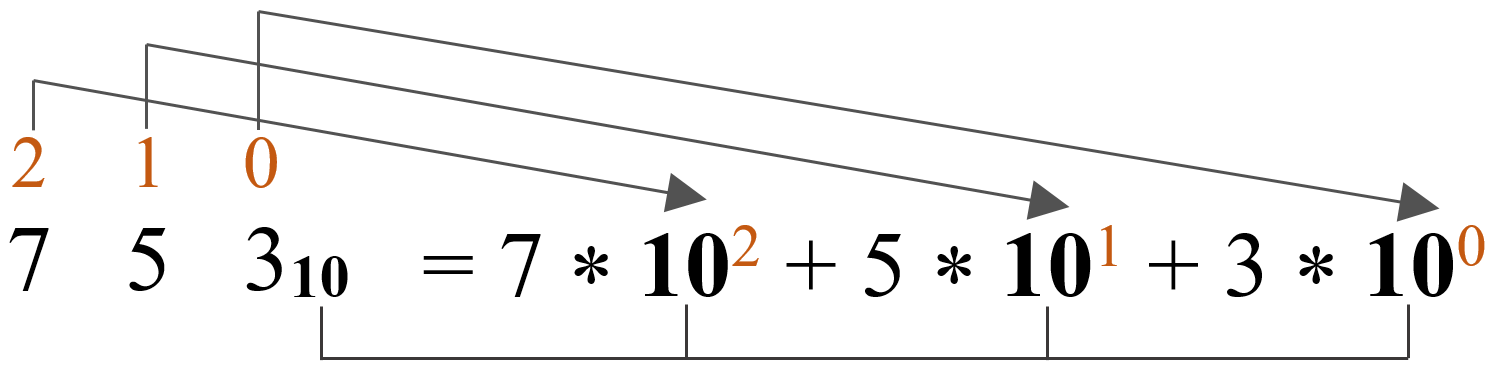
Каждую цифру в числе, умножим в соответствии занимаемой позицией:
Для упрощения данной записи, представим данное число, как основание 10 в степени n:
Запишем полученный результат.
Обратите внимание, что степень основания числа совпадает с позицией каждой цифры в числе!
Перевод числа в десятичную систему счисления
С помощью развёрнутой формы представления чисел можно перевести число из любой системы счисления в десятичную.
✒ Определение: каждую цифру числа нужно умножить на его основание, возведённое в степень, равную позиции цифры в числе.
Двоичная система счисления
Алфавит системы счисления: 0, 1.
Перевод десятичного числа в двоичную систему счисления методом подбора степеней числа 2
Для перевода двоичных чисел в десятичную систему счисления, используют метод подбора степеней двойки.
Пусть дано десятичное число 2110.
1) Подберём ближайшую наименьшую степень числа 2 к данному числу: 2 4 = 16;
3) Повторить, пока не достигнем нуля.
В результате, мы получим следующие степени:
Найденные нами степени – это позиции цифры 1 в двоичном числе, а отсутствующие степени – это нули:
Перевод целого десятичного числа в другую систему счисления методом деления на новое основание
✒ Определение: Для перевода целого десятичного числа в другую систему счисления, необходимо делить данное число на новое основание (той системы счисления, в которую необходимо осуществить перевод). Ответ складывается из остатков от деления.
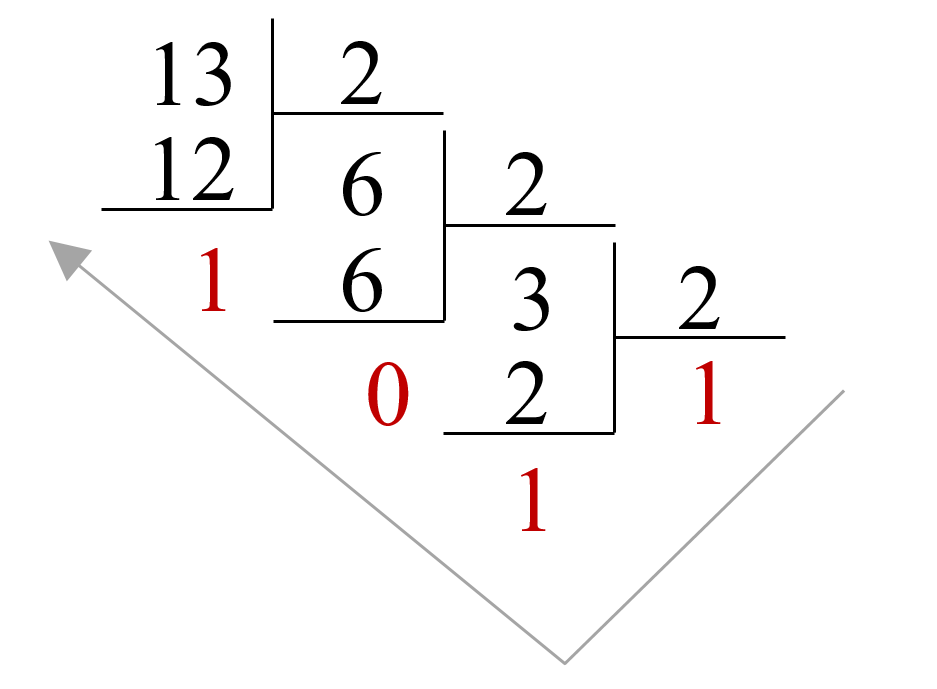
Переведите число 1310 в двоичную систему счисления.
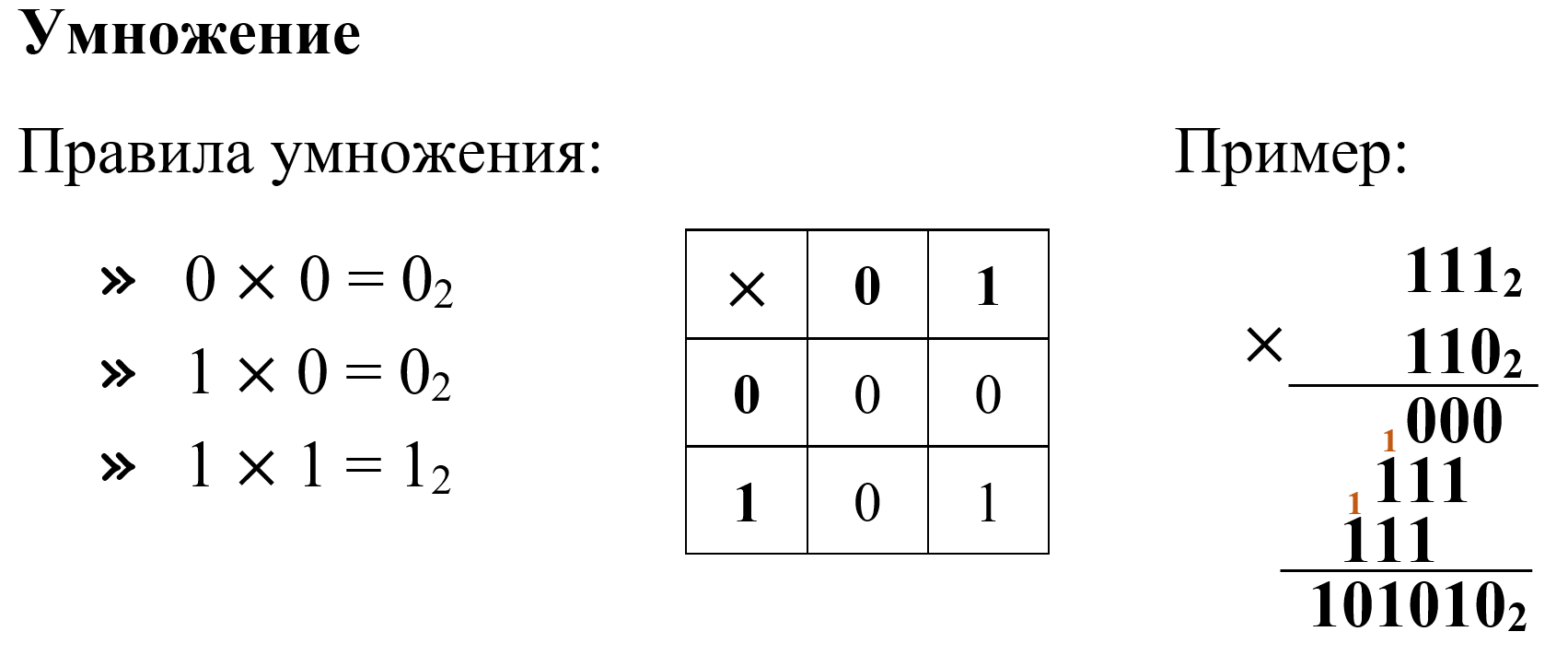
Арифметические операции в двоичной системе счисления
Все вычисления в компьютере выполняются в двоичной системе счисления.
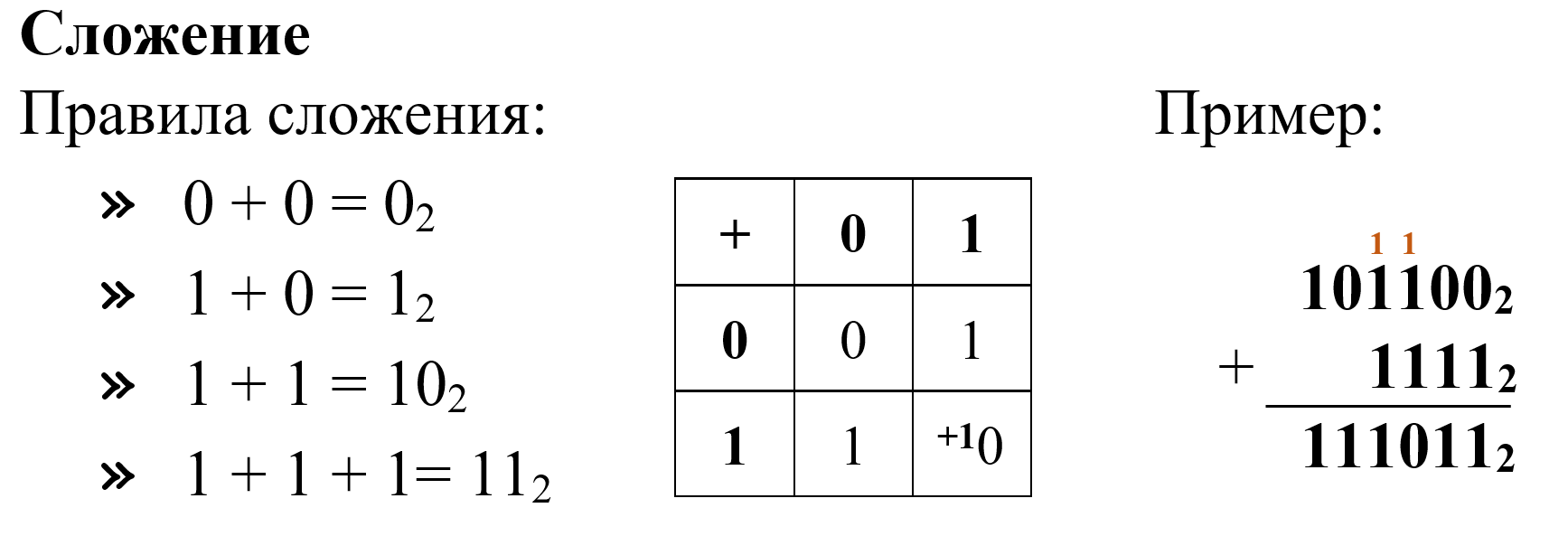
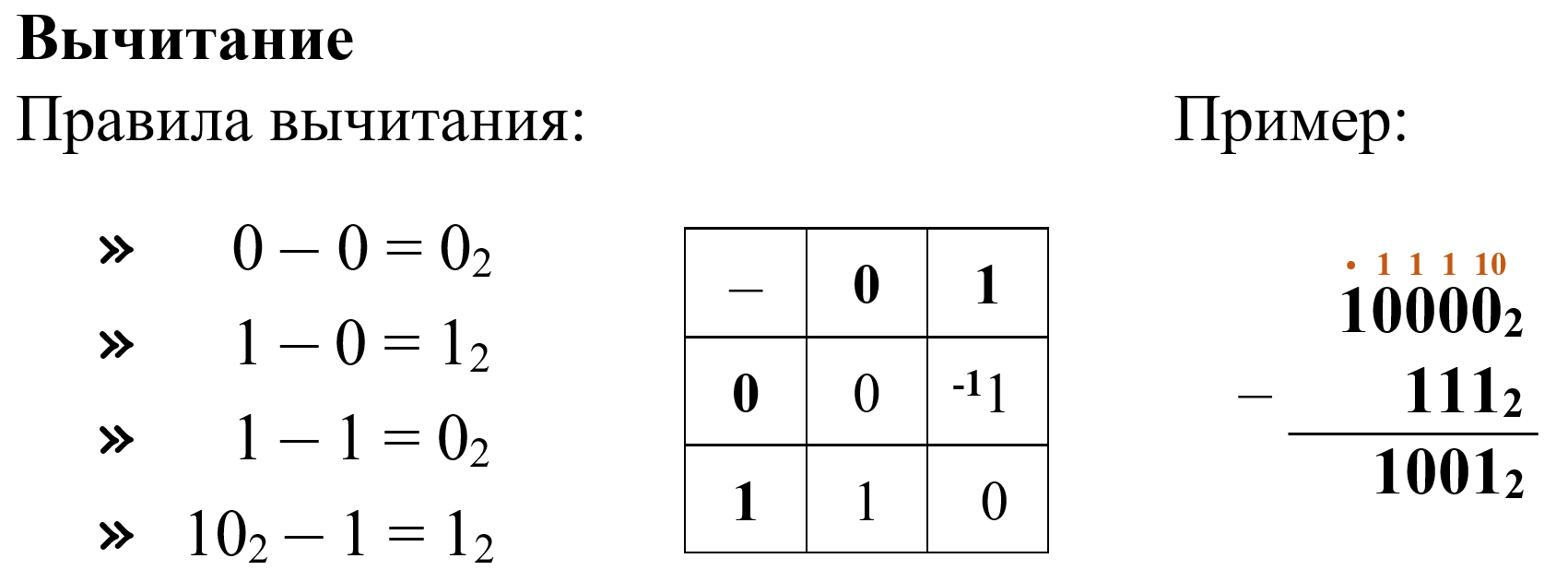
Рассмотрим базовые арифметические операции.
Кодирование числовой информации в памяти компьютера
Для представления целого числа без знака в памяти компьютера, необходимо:
1. перевести число в двоичную систему счисления;
2. поместить число в ячейку памяти компьютера;
3. заполнить пустые ячейки незначащими нулями.
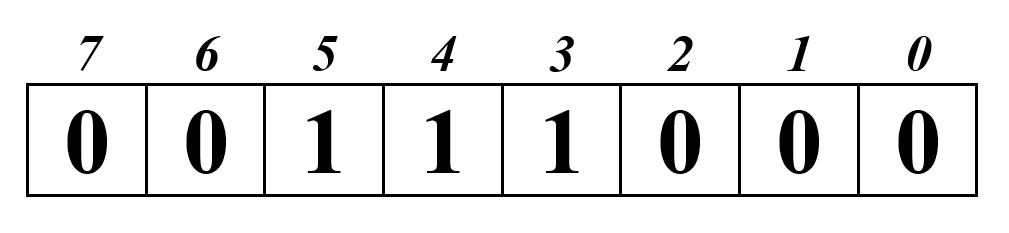
Представьте число 5610 в компьютерной форме.
1. переведём число в двоичную систему счисления:
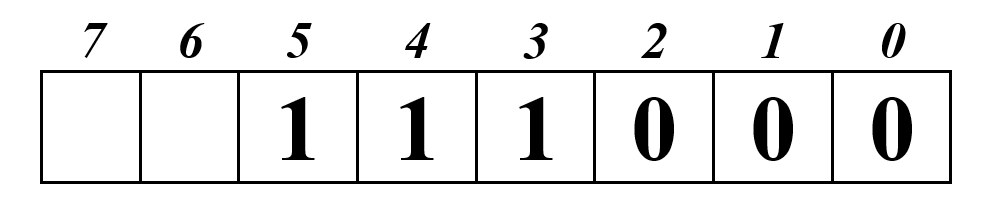
2. число состоит из 6 разрядов и помещается в одну ячейку:
3. дополним незначащими нулями:
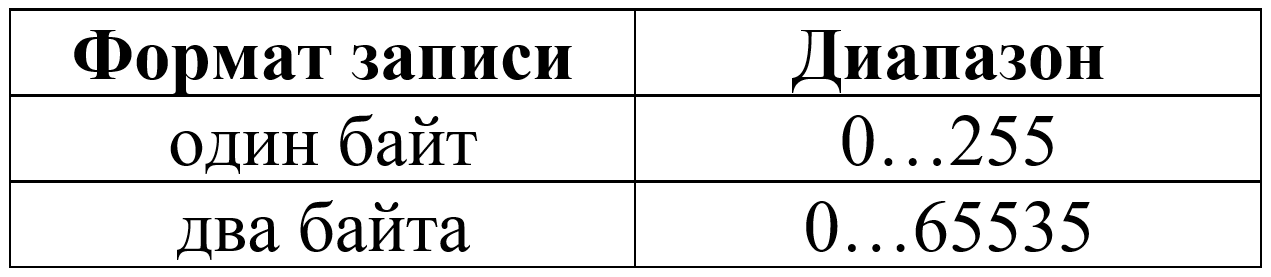
Диапазон значений целых чисел без знака
Хранение чисел со знаком отличается от беззнаковой формы.
Знак «+» принято обозначать за «0», а знак «–» за «1». Знак записывается в старший бит ячейки. Для хранения таких чисел выделяют 1, 2 или 4 байта.
Для представления целого числа со знаком «+» в памяти компьютера, необходимо:
1. перевести число в двоичную систему счисления;
2. поместить число в ячейку памяти;
3. выделить старший бит ячейки под знак и поставить на это место нуль.
4. заполнить оставшиеся биты незначащими нулями.
Представьте число +29210 в компьютерной форме.
1. переведём число в двоичную систему счисления:
2. число состоит из 9 разрядов и для хранения требует двух ячеек:
3. число положительное, значит в старший бит необходимо поместить нуль:
4. заполним оставшиеся биты незначащими нулями:
Для представления целого числа со знаком «–» в памяти компьютера применяют метод прямого и обратного кода:
1. перевести модуль данного числа в двоичную систему;
2. Прямой код: поместить число в ячейку памяти и дополнить его незначащими нулями;
3. Обратный код: выполнить инверсию (заменить нули на единицы и наоборот);
4. Дополнительный код: увеличить получившееся число на единицу.
Представьте число –8710 в компьютерной форме.
1. переведём модуль числа в двоичную систему счисления:
2. число состоит из 7 разрядов и помещается в одну ячейку. Поместим число в ячейку и дополним незначащими нулями:
4. прибавляем к числу единицу:
Обратите внимание на старший бит. Здесь 1 – это знак числа.
Переводы
1. Выполните перевод чисел из двоичной системы счисления в десятичную систему методом развёрнутой формы представления числа:
| а) 11002 | д) 11000112 | з) 10011101110002 |
| б) 110002 | е) 1001011012 | к) 10010000101112 |
| в) 1010102 | ж) 1011101102 | л) 1011101011112 |
| г) 11000112 | з) 1111112 | м) 11111112 |
2. Выполните перевод из десятичной системы счисления в двоичную методом подбора степеней числа 2:
| а) 42 | д) 232 | з) 400 |
| б) 97 | е) 286 | к) 405 |
| в) 111 | ж) 309 | л) 528 |
3. Выполните перевод из десятичной системы счисления в двоичную методом деления на новое основание:
| а) 20 | д) 100 | з) 568 |
| б) 31 | е) 102 | к) 443 |
| в) 49 | ж) 127 | л) 500 |
| г) 96 | з) 269 | м) 600 |
Арифметические операции в двоичной СС
4. Выполните сложение чисел:
| а) 10012 + 11002 | д) 1000012 + 110002 |
| б) 10102 + 10102 | е) 1011102 + 10101002 |
| в) 1110012 + 1101102 | ж) 10111112 + 10111112 |
| г) 1010102 + 1100112 | з) 11110112 + 11110012 |
5. Выполните вычитание чисел:
6. Выполните умножение чисел:
| а) 11002 × 1012 | д) 1011002 × 10112 |
| б) 10102 × 1112 | е) 1011112 × 11012 |
| в) 110112 × 10112 | ж) 1011012 × 11112 |
| г) 111102 × 10112 | з) 1010112 × 11102 |
7. Найти значение выражения:
Кодирование чисел
8. Представьте целое десятичное число со знаком в памяти компьютера. Сколько ячеек памяти нужно выделить для хранения данного числа?
| а) +25 | д) +204 | з) +512 |
| б) +64 | е) +212 | к) +4096 |
| в) +96 | ж) +256 | л) +32256 |
| г) +128 | з) +302 | м) +65536 |
9. Представьте целое десятичное число со знаком в памяти компьютера. Сколько ячеек памяти нужно выделить для хранения данного числа?
10. Дано внутреннее представление целого числа со знаком. Какому десятичному числу оно соответствует?
Как записать число в развернутой форме информатика
2.5. РАЗВЕРНУТАЯ ФОРМА ЧИСЛА
Развернутая форма записи числа – это запись в виде разрядных слагаемых, записанных с помощью степени соответствующего разряда и основания степени (основание счета).
1. Десятичная система:
Пронумеруем разряды, начиная с младшего:
Теперь запишем выражение:
2. Двоичная система:
Пронумеруем разряды, начиная с младшего:
3. Шестнадцатеричная система:
Пронумеруем разряды, начиная с младшего:
Другие системы счисления записываются аналогично вышеприведенным системам с тем лишь исключением, что основание степени будет соответствовать основанию счета.
В позиционной системе счисления число можно представить в развернутой форме (в виде суммы разрядных слагаемых) и в свернутой форме. Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.
Десятичное число А10= 4718,63 в развернутой форме будет имеет вид:
Рассмотрим еще примеры записи чисел в развернутом виде
58910 → 500 + 80 + 9 = 5*100 + 8*10 + 9*1 = 5*10 2 +8*10 1 + 9*10 0

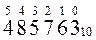
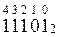

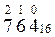
Задания для самостоятельной работы
Задание 1. Запишите числа в развернутой форме
| 1) | 11110102 | 6) | 111101,0012 | 11) | 1110,112 | 16) | 100011102 |
| 2) | 2174,55 | 7) | 5771,0015 | 12) | 89784515 | 17) | 514763175 |
| 3) | 6479118 | 8) | 1622,848 | 13) | 1114878 | 18) | 113874,3348 |
| 4) | 1214710 | 9) | 512001410 | 14) | 1874,59610 | 19) | 1554,01410 |
| 5) | 1247,032116 | 10) | 15789416 | 15) | 163201,9816 | 20) | 88541216 |
Перевод чисел в десятичную систему счисления
1. Записать число в развернутом виде
2. Выполнить вычисления как в десятичной системе счисления
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10571 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, программирование, полезный материал и многое другое.
Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
Ответ
Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
Переход от свернутой формы к развернутой
1. Посмотрите на данное вам число и определите количество его цифр.
Пример:
Напишите 5827 в развернутом виде.
Прочитайте число вслух: пять тысяч восемьсот двадцать семь.
Обратите внимание, что в этом числе есть четыре цифры. В результате развернутая форма будет содержать четыре слагаемых.
2. Перепишите число в виде суммы его цифр, оставив между ними некоторое расстояние, чтобы умножить каждую цифру на некоторую цифру (об этом далее).
Пример:
5827 перепишите так:
3. Цифры числа расположены в определенных позициях, которые соответствуют (справа налево) единицам, десяткам, сотням, тысячам и так далее. Определите название позиции и ее значение для каждой цифры (справа налево).
Пример:
Так как в данном числе четыре цифры, то вам нужно определить названия четырех позиций (справа налево).
7 соответствует единицам (значение = 1 = 10 0 ).
2 соответствует десяткам (значение = 10 = 10 1 ).
8 соответствует сотням (значение = 100 = 10 2 ).
5 соответствует тысячам (значение = 1000 = 10 3 ).
4. Умножьте каждую цифру данного числа на значение соответствующей ей позиции.
Пример:
5 · 10 3 + 8 · 10 2 + 2 · 10 1 + 7 · 10 0
Как записать двоичное число в развернутой форме
Электронные облака
Лекции
Рабочие материалы
Тесты по темам
Template tips
Задачи
Логика вычислительной техники и программирования
Лекция «Системы счисления»
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.
Символы, при помощи которых записывается число, называются цифрами.
В конце концов, самой популярной системой счисления оказалась десятичная система. Десятичная система счисления пришла из Индии, где она появилась не позднее VI в. н. э. В ней всего 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 но информацию несет не только цифра, но также и место позиция, на которой она стоит. В числе 444 три одинаковых цифры обозначают количество и единиц, и десятков, и сотен. А вот в числе 400 первая цифра обозначает число сотен, два 0 сами по себе вклад в число не дают, а нужны лишь для указания позиции цифры 4.
Классификация систем счисления
Системы счисления подразделяются на позиционные и непозиционные.
Позиционные системы счисления
Путем долгого развития человечество пришло к созданию позиционного принципа записи чисел, который состоит в том, что каждая цифра, содержащаяся в записи числа, занимает определенное место, называемое разрядом. Отсчет разрядов производится справа налево. Единица каждого следующего разряда всегда превосходит единицу предыдущего разряда в определенное число раз. Это отношение носит название основание системы счисления (у непозиционных систем счисления понятия «разряда» и «основания» отсутствуют).
Общее свойство всех позиционных систем счисления: при каждом переходе влево (вправо) в записи числа на один разряд величина цифры увеличивается (уменьшается) во столько раз, чему равно основание системы счисления.
Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. Например: Римская система счисления.
Из многочисленных представителей этой группы в настоящее время сохранила свое значение лишь римская система счисления, где для обозначения цифр используются латинские буквы:
| I | V | X | L | С | D | М |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
С их помощью можно записывать натуральные числа. Например, число 1995 будет представлено, как MCMXCV (М-1000,СМ-900,ХС-90 и V-5).
Правила записи чисел в римской системе счисления:
Например, запись XXX обозначает число 30, состоящее из трех цифр X, каждая из которых, независимо от места ее положения в записи числа, равна 10. Запись MCXX1V обозначает 1124, а самое большое число, которое можно записать в этой системе счисления, это число MMMCMXCIX (3999). Для записи еще больших чисел пришлось бы вводить все новые обозначения. По этой причине, а также по причине отсутствия цифры ноль, римская система счисления не годится для записи действительных чисел.
Таким образом, можно констатировать следующие основные недостатки непозиционных систем счисления:
Алфавит и основание системы счисления
Алфавитом системы счисления называется совокупность различных цифр, используемых в позиционной системе счисления для записи чисел. Например:
Десятичная система: <0, 1, 2, 3, 4, 5, 6, 7, 8, 9>
Двоичная система: <0, 1>
Восьмеричная система: <0, 1, 2, 3, 4, 5, 6, 7>
Шестнадцатеричная система:
Количество цифр в алфавите равно основанию системы счисления. Основанием позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
Позиция цифры в числе называется разрядом: разряд возрастает справа налево, от младших к старшим, начиная с нуля.
Развёрнутая форма представления числа
Системы счисления, используемые в вычислительной технике
Несмотря на то, что исторически человек привык работать в десятичной системе счисления, с технической точки зрения она крайне неудобна, так как в электрических цепях компьютера требовалось бы иметь одновременно десять различных сигналов. Тем не менее, такие схемы существуют в некоторых видах микрокалькуляторов.
Чем меньше различных сигналов в электрических цепях, тем проще микросхемы, являющиеся основой конструкции большинства узлов ЭВМ, и тем надежнее они работают.
Наименьшее основание, которое может быть у позиционных систем счисления это – двойка. Именно поэтому двоичная система счисления используется в вычислительной технике, а двоичные наборы приняты за средство кодирования информации. В компьютере имеются только два устойчивых состояния работы микросхем, связанных с прохождением электрического тока через данное устройство (1) или его отсутствием (0). Говоря точнее, (1) кодирует высокое напряжение в схеме компьютера, а (0) – низкое напряжение.
Если вспомнить, что двоичная система счисления обладает самыми маленькими размерами таблиц сложения и умножения, то можно догадаться, что этот факт должен сильно радовать конструкторов ЭВМ, поскольку обработка сигнала в этом случае будет также самой простой. Таким образом, двоичная система счисления, с точки зрения организации работы ЭВМ, является наилучшей.
Мы уже говорили о преимуществах двоичной системы счисления с технической точки зрения организации работы компьютера. Зачем нужны другие системы счисления, кроме, естественно, еще и десятичной, в которой человек привык работать? Чтобы ответить на него, возьмем любое число в десятичной системе счисления, например 255, и переведем его в другие системы счисления с основаниями, кратными двойке:
Чем меньше основание системы счисления, тем больше разрядов требуется для его записи то есть, тем самым мы проигрываем в компактности записи чисел и их наглядности. Поэтому, наряду с двоичной и десятичной системами счисления, в вычислительной технике применяют так же запись чисел в 8-и 16-ричных системах счисления. Поскольку их основания кратны двойке, они органично связаны с двоичной системой счисления и преобразуются в эту систему наиболее быстро и просто (по сути они являются компактными видами записи двоичных чисел). Все другие системы счисления представляют для вычислительной техники чисто теоретический интерес.
Решение задач
1. Какое число записано с помощью римских цифр: CLVI
Решение: Зная обозначения, запишем: С – 100; L – 50; V – 5; I – 1
Решение: Пользуемся формулой:
a1 = 3; a2 = B; a3 = F; a4 = A
Следовательно: 3ВFA16 = 3*16 3 + B*16 2 + F*16 1 + A*16 0
Ответ: 3ВFA16 = 3*16 3 + B*16 2 + F*16 1 + A*160
3. Запишите в свёрнутой форме число 1*8 2 + 4*8 1 + 7*8 0
Решение: Пользуемся формулой:
Следовательно: 1*8 2 + 4*8 1 + 7*8 0 = 1478
Ответ: 1*8 2 + 4*8 1 + 7*8 0 = 1478
Алгоритмы перевода в системы счисления по разным основаниям
Алгоритм перевода чисел из любой системы счисления в десятичную
Алгоритм перевода целых чисел из десятичной системы счисления в любую другую
Алгоритм перевода правильных дробей из десятичной системы счисления в любую другую
Алгоритм перевода произвольных чисел из десятичной системы счисления в любую другую
Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2 n
Решение задач
1. Переведём в 10-ую с.с. число: 0,1235
Решение: Действуем строго по алгоритму перевода чисел из любой системы счисления в десятичную:
Найдём сумму ряда: 0,2 + 0,08 + 0,024 = 0,30410
Ответ: 0,1235 = 0,30410
2. Переведём число 12610 в 8-ую с.с. и число 18010 в 16-ую с.с.
Решение: Действуем строго по алгоритму перевода целых чисел из 10-ой с.с. в любую другую:
Во втором примере процесс можно продолжать бесконечно. В этом случае деление продолжаем до тех пор, пока не получим нужную точность представления. Записываем числа сверху вниз.
Ответ: 0,6562510 = 0,А816; 0,910 = 1,1110012 с точностью до семи значащих цифр после запятой.
4. Переведём число 124,2610 в шестнадцатеричную с.с.
Решение: Действуем строго по алгоритму перевода произвольных чисел:
Переводим целую и дробную часть:
Записываем полученные числа справа налево (в целой части) и сверху вниз (в дробной части).
Ответ: 124,2610 = 7С,428А16
5. Переведём число: 11001010011010101112 в шестнадцатеричную систему счисления
Решение: Действуем строго по алгоритму перевода чисел из 2-ой с.с в с.с. с основанием 2 n :