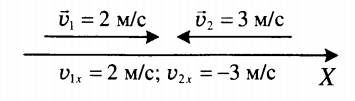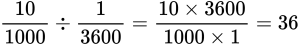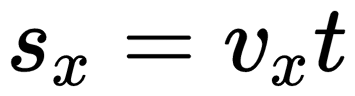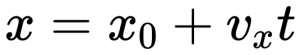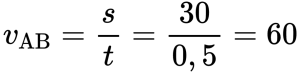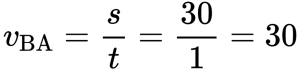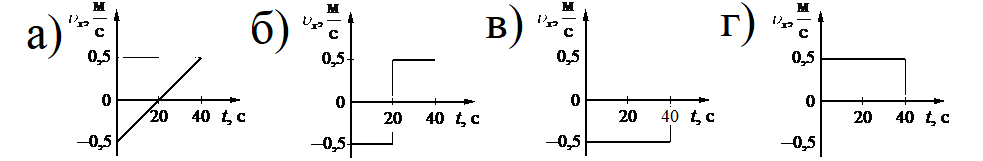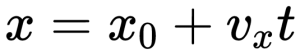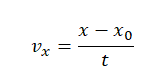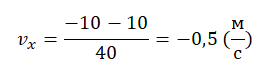как записывается в векторной форме уравнение равномерного

Как записывается в векторной форме уравнение равномерного

§ 12. Уравнения равномерного прямолинейного движения

1. Уравнение в векторной форме.

Знаем, что одна из основных задач механики заключается в нахождении положения точки в любой момент времени при движении. Знаем, что положение точки может быть определено радиус-вектором, и в любом движении конечный радиус-вектор имеет вид:

.

— задан, а наиболее просто находить в равномерном прямолинейном движении с помощью скорости и времени.

— это и есть уравнение равномерного прямолинейного движения в векторной форме.

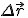
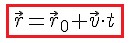
2. Уравнение в координатной форме.

Знаем, что векторы находят с помощью проекций на оси координат. Поэтому от векторного уравнения движения перейдём к проекциям векторных величин на оси координат.

Если , то:

.

Проекции радиусов равны соответствующим координатам. Поэтому:

.

Если траектория известна, то мы совмещаем траекторию с осью координат OX и пользуемся вместо трёх всего одним первым уравнением.

Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.

Источник

Физика. 10 класс

Равномерное прямолинейное

Равномерное прямолинейное движение материальной точки

Необходимо запомнить

Основная задача механики – определить положение тела в пространстве в любой момент времени.

Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени.

Закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение.

Материальная точка – тело, размерами которого в рассматриваемом случае можно пренебречь.

Тело, относительно которого рассматривается движение, – тело отсчёта.

Совокупность тела отсчёта, связанной с ним системы координат и часов называют системой отсчёта.

Траектория – линия, вдоль которой двигалось тело.

Длину траектории называют пройденным путём.

Перемещением тела (материальной точки) называют вектор, соединяющий начальное положение тела с его последующим положением.

Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.

Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Решение задачи

Из истории изучения движения

В истории человечества были и драматические случаи, связанные с выбором системы отсчета. Казнь Джордано Бруно, отречение Галилео Галилея – все это следствия борьбы между сторонниками геоцентрической системы отсчёта и гелиоцентрической системой отсчёта. Сложно было человечеству привыкнуть к мысли о том, что Земля вполне обычная планета, а вовсе не центр мироздания. А движение можно рассматривать не только относительно Земли, но и относительно Солнца, звёзд или любых других тел. Намного удобнее и проще описывать движение небесных тел в системе отсчёта, связанной с Солнцем, это убедительно показали сначала Кеплер, а потом и Ньютон. Свой знаменитый закон всемирного тяготения Ньютон вывел на основании рассмотрения движения Луны вокруг Земли.

Источник

Уравнение движения, графики равномерного прямолинейного движения

п.1. Прямолинейное равномерное движение на координатной прямой

Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.

Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:

Стартуя с точки x₀=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: \begin x=x_0+s=x_0+vt\\ x=20+10t \end

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:

В этом случае координата x в любой момент времени t имеет вид: \begin x=x_0-st=x_0-vt\\ x=20-10t \end Если же машина никуда не едет, её скорость v=0, и координата x=x₀ в любой момент времени t.

п.2. Уравнение прямолинейного равномерного движения

Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.

п.3. Удобная система отсчета для решения задачи о прямолинейном движении

При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.

При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.

Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.

п.4. График движения x=x(t)

Сравним полученное уравнение движения \(x(t)=x_0+v_x t\) с уравнением прямой \(y(x)=kx+b\) (см. §38 справочника по алгебре для 7 класса).

В уравнении движения роль углового коэффициента \(k\) играет проекция скорости \(v_x\), а роль свободного члена \(b\) – начальная координата \(x_0\).

Построим графики зависимости координаты от времени для нашего примера:

п.5. Как найти уравнение движения по графику движения?

п.6. График скорости v_x=v_x(t)

Для рассмотренного примера:

п.7. Как найти путь и перемещение по графику скорости?

Проекция перемещения может быть как положительной, так и отрицательной или равной 0.

п.8. Задачи

Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите \(x_0=0\) и запишите уравнение движения.
а) Постройте график движения \(x=x(t)\) и найдите с его помощью, сколько пробежит спортсмен за \(t_1=5\ с\), за \(t_2=10\ с\);
б) постройте график скорости \(v=v(t)\) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени \(\triangle t=t_2-t_1\)?

По условию \(x_0=0,\ v_x=8\).
Уравнение движения: \(x=x_0+v_x t=0+8t=8t\)
а) Строим график прямой \(x=8t\) по двум точкам:

Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?

б) В начальный момент времени корабль находился на расстоянии \(x_0=20\) тыс.км от астероида.

Источник

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

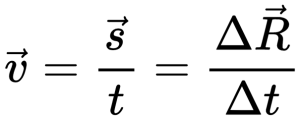
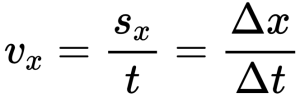
Векторный способ записи скорости при равномерном прямолинейном движении: s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

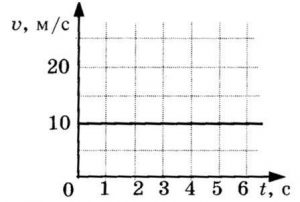
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

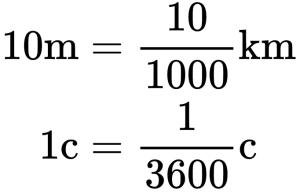
Перемещение и координаты тела при равномерном прямолинейном движении

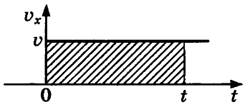
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

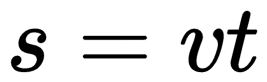
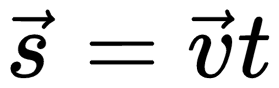
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

Пример №2. График зависимости координаты тела от времени имеет вид:

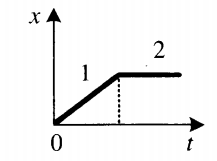
Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

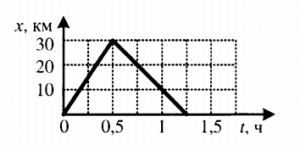
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Алгоритм решения

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁ и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁ и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

§ 4. Равномерное прямолинейное движение. Скорость. Уравнение движения (окончание)

Графическое представление равномерного прямолинейного движения

Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (рис. 1.11). Это прямая, параллельная оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть υ_x, а сторона ОС — время движения t, поэтому Δ_x = υ_xt.

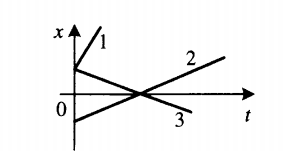
На рисунке 1.12 приведены примеры графиков зависимости координаты от времени для трёх различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х₀ = 0, υ_x1 > 0; прямая 2 — случаю х₀ 0, а прямая 3 — случаю х₀ > 0, υ_x3 Образцы заданий ЕГЭ

A1. Зависимость координаты точки от времени при равномерном прямолинейном движении выражается

1) линейной функцией 3) тригонометрической функцией
2) квадратичной функцией 4) показательной функцией

A3. В таблице приведены координаты корабля, плывущего по прямому каналу.

Согласно данным таблицы, движение корабля является

1) равномерным в течение всего времени наблюдения

2) неравномерным в течение всего времени наблюдения

3) равномерным первые 10 мин наблюдения и неравномерным с 10-й по 30-ю мин

4) неравномерным первые 10 мин наблюдения и равномерным с 10-й по 30-ю мин

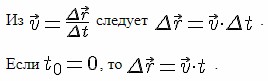
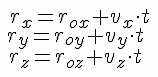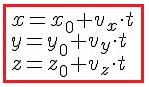Источник