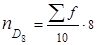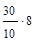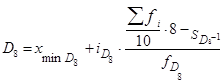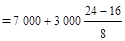Укажите что является структурной средней выберите 2 варианта
Структурные средние
Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака.
В качестве структурных средних чаще всего используют показатели моды и медианы.
1. Мода – наиболее часто повторяющееся значение признака в изучаемой совокупности.
Для дискретных рядов распределения модой будет то значение признака, у которого наибольший удельный вес. В интервальных рядах распределения с равными интервалами мода определяется по формуле:
Мо = 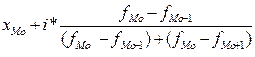
где 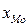
i – величина модального интервала;
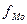

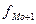
Мода широко применяется в коммерческой деятельности.
2. Медиана – величина признака, которая делит упорядоченную последовательность его значений на 2 равные по численности части.
Если ряд распределения дискретный и имеет нечетное число значений, то медианой будет значение признака, находящееся в середине упорядоченного ряда. Например, стаж пяти рабочих составил 2, 4, 7, 8 и 10 лет. В таком упорядоченном ряду медиана – 7 лет.
Если упорядоченный ряд состоит из четного числа значений, то медианой будет средняя арифметическая из 2 значений признака, расположенных в середине ряда. Пусть в бригаде не 5 человек, а 6, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В центре ряда стоят 6 и 7, т. е. средняя арифметическая этих значений и будет медианой ряда: Ме = (6+7)/2=6,5 лет.
В интервальном вариационном ряду медиана определяется по формуле:
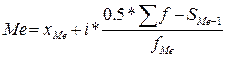
где 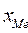
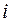

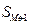
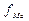
Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала, в котором находится медиана, т.е. медианного интервала – этот интервал характеризуется тем, что его кумулятивная частота равна полусумме или превышает полусумму всех частот ряда.
Медиана используется при контроле качества продукции и технологического процесса на промышленных предприятиях, а также при изучении распределения домохозяйств по величине дохода.
Мода и медиана являются дополнительными к средней величине характеристиками совокупности и используются в статистике для анализа формы рядов распределения.
Если значение средней величины совпадает с модой и медианой, то ряд является симметричным. На практике строго симметричные ряды встречаются довольно редко, чаще исследователю приходится иметь дело с асимметричными рядами. Простейшим показателем асимметрии может служить разность между средней арифметической величиной и модой.
Если AS = 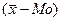
К структурным характеристикам исследуемой совокупности относятся также:
— квартили, делящие совокупность на 4 равные части,
— квинтили, делящие совокупность на 5 равных частей;
— децили, делящие совокупность на 10 частей,
— перцентили, делящие совокупность на 100 частей.
Вопросы для самоконтроля
1. Что такое статистический показатель? Какие виды статистических показателей Вы знаете?
2. Каково значение абсолютных величин в статистике? В каких единицах они измеряются? Приведите примеры.
3. Что характеризуют относительные статистические показатели? На какие виды они делятся?
4. Дайте определение средней величины.
5. Какие виды средних величин применяются в статистике?
6. В каких случаях применяются степенные средние?
7. Какие свойства средней арифметической Вы знаете?
8. Для чего используются структурные средние? На какие виды они подразделяются?
Глава 4. Вариация признака
Цель:усвоить и закрепить материал по теме, научиться проводить анализ вариационных рядов.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Структурные средние величины
Структурные (позиционные) средние – это средние величины, которые занимают определенное место (позицию) в ранжированном вариационном ряду.
Для дискретных вариационных рядов модой будет значение варианты с наибольшей частотой
Пример. Определить моду по имеющимся данным (табл. 7.5).
Таблица 7.5 – Распределение женской обуви, проданной в обувном магазине N, февраль 2013 г.
| Размер обуви | Число купленных пар |
| Итого |
По данным табл. 5 видно, что наибольшая частота fmax = 28, ей соответствует значение признака x = 37 размер. Следовательно, Mo = 37 размер обуви, т.е. именно этот размер обуви пользовался наибольшим спросом, наиболее часто покупали обувь 37-го размера.
В интервальном вариационном ряду сначала определяется модальный интервал, т.е. содержащий моду – интервал с наибольшей частотой (в случае интервального распределения с равными интервалами, в случае с неравными интервалами – по наибольшей плотности).
Модой приближенно считается середина модального интервала. Конкретное значение моды для интервального ряда определяется по формуле:
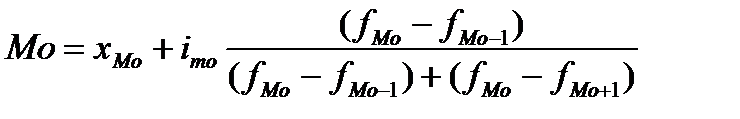
где xMo – нижняя граница модального интервала;
iMo – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Пример. Определить моду по имеющимся данным (табл. 7.6).
Таблица 7.6 – Распределение работников по стажу
| Стаж, лет | Число работников, чел. |
| до 2 2-4 4-6 6-8 8-10 свыше 10 | |
| Итого |
По данным табл. 6 видно, что наибольшая частота fmax = 35, ей соответствует интервал: 6-8 лет (модальный интервал). Определим моду по формуле:
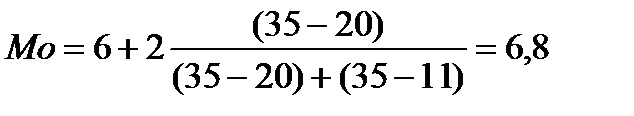
Следовательно, Mo = 6,8 лет, т.е. большинство работников имеют стаж 6,8 лет.
Название медианы взято из геометрии, где им именуется отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны и разделяющий, таким образом, сторону треугольника на две равные части.
Медиана(Mе) – это значение признака, приходящееся на середину ранжированной совокупности. Иначе медиана – это величина, которая делит численность упорядоченного вариационного ряда на две равные части – одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Пример. В ряду из 51 члена номер медианы (51+1)/2 = 26, т.е. медианой является вариант, стоящий в ряду 26-ым по порядку.
Дляранжированного ряда с четным числом членов (n=чет) – медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда. Порядковые номера двух центральных вариант определяются следующим образом:
Пример. При n=50; NMe1 = 50/2 = 25; NMe2 = (50/2)+1 = 26, т.е. медианой является средняя из вариант, стоящих в ряду 25-ой и 26-ой по порядку.
В дискретных вариационных рядах медиана находится по накопленной частоте, соответствующей порядковому номеру медианы или впервые его превышающей. Иначе по накопленной частоте равной или впервые превышающей половину суммы всех частот ряда.
Пример. Определить медиану по имеющимся данным (табл. 7.7).
Таблица 7.7 – Распределение женской обуви, проданной в обувном магазине N, февраль 2013 г.
| Размер обуви | Число купленных пар | Накопленные частоты | % к итогу |
| Итого | х | х |
По данным табл. 7 определим порядковый номер медианы: NMe=(67+1)/2=34. Накопленная частота, впервые превышающая это значение, S = 41, ей соответствует значение признака x = 37 размер. Следовательно, Me = 37 размер обуви, т.е. половина пар покупается меньше 37-го размера, а другая половина – больше.
В этом примере мода и медиана совпадают, но они могут и не совпадать.
В интервальном вариационном ряду определяются накопленные частоты, по данным о накопленных частотах находят медианный интервал – интервал, в котором накопленная частота составляет половину или впервые превышает половину всей суммы частот. Формула для определения медианы в интервальном ряду распределения имеет следующий вид:
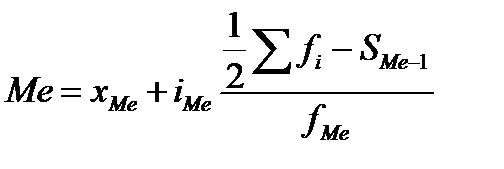
где xMe – нижняя граница медианного интервала;
iMe – величина медианного интервала;
SMe-1 – сумма накопленных частот интервала, предшествующего медианному;
fMe – частота медианного интервала.
Пример. Определить медиану по имеющимся данным (табл. 7.8).
Таблица 7.8 – Распределение работников по стажу
| Стаж, лет | Число работников, чел. | Накопленные частоты |
| до 2 2-4 4-6 6-8 8-10 свыше 10 | ||
| Итого | х |
По данным табл. 8 определим порядковый номер медианы: NMe=100/2=50. Накопленная частота, впервые превышающая это значение, S = 82, ей соответствует интервал 6-8 лет (медианный интервал). В этом примере модальный и медианный интервал совпадают, но они могут и не совпадать. Определим медиану по формуле:
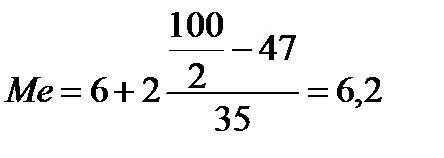
Следовательно, Me = 6,2 года, т.е. половина работников имеют стаж менее 6,2 года, а другая половина – более.
Мода и медиана находят широкое применение в разных областях экономики. Так, исчисление модальной производительности труда, модальной себестоимости и т.д. дает возможность экономисту судить о преобладающем в данный момент их уровне. Эта характеристика должна быть использована для выявления резервов нашей экономики. Мода имеет значение для решения практических задач. Так, при планировании массового выпуска одежды и обуви устанавливается размер продукции, который пользуется наибольшим спросом (модальный размер). Мода может быть использована в качестве приближенной характеристики уровня изучаемого признака вместо средней арифметической, если распределения частот близко к симметричному и имеет одну неплоскую вершину.
Медиану следует применять в качестве средней величины в тех случаях, где нет достаточной уверенности в однородности изучаемой совокупности. На медиану влияют не столько сами значения, сколько число случаев на том или ином уровне. Следует также отметить, что медиана всегда конкретна (при большом числе наблюдений или в случае нечетного числа членов совокупности), т.к. под Ме подразумевается некоторый действительный реальный элемент совокупности, тогда как арифметическая средняя часто принимает такое значение, которое не может принимать ни одна из единиц совокупности.
Главное свойство Ме в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины: 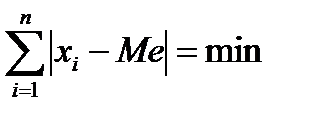
В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место в ранжированном вариационном ряду (каждое четвертое, пятое, десятое, двадцать пятое и т.д.). Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда.
Для расчета квартилей по интервальному ряду используют формулы:
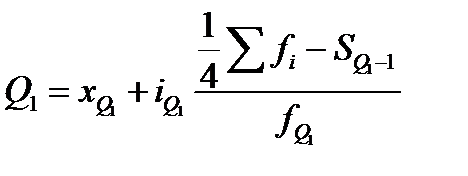
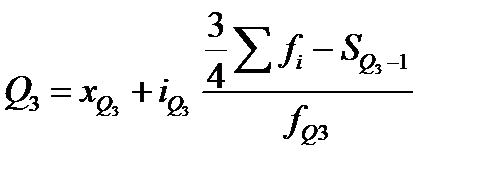
где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1 – частота интервала, содержащего нижний квартиль;
fQ3 – частота интервала, содержащего верхний квартиль.
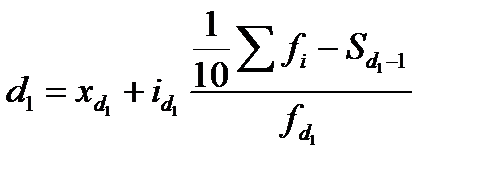
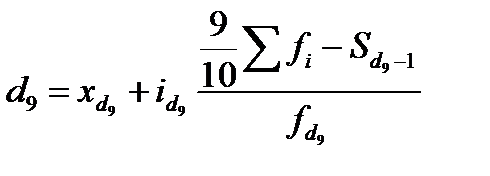
Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет глубоко и детально охарактеризовать изучаемую совокупность.
Статистика
Структурные средние
Структурные средние
Особый вид средних величин – структурные средние – применяются для изучения внутреннего строения рядов распределения значений признака. К таким показателям относятся мода и медиана.
Модой (Мо) называется чаще всего повторяющееся значение признака, а медианой (Ме) – величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части.
Мода широко используется в коммерческой практике при изучении покупательского спроса, например, при определении размеров одежды и обуви, которые пользуются широким спросом.
Если изучаемый признак имеет дискретные значения, то для определения моды достаточно подсчитать частоты отдельных значений и определить среди них наибольшую (на практике может быть несколько значений моды), а для определения медианы необходимо упорядочить ряд и найти средний по порядку элемент (при четном количестве отдельных единиц, можно вычислить медиану как полусумму двух средних элементов).
Пусть получены следующие значения признака:
12,5 14 13 11,5 12,5 16 12
Для этого ряда значений модой будет являться число – 12,5. Медианой будет являться число 12,5 (значения предварительно следует расположить по возрастанию).
Если изучаемый признак имеет дискретные значения, то для определения моды достаточно подсчитать частоты отдельных значений и определить среди них наибольшую (на практике может быть несколько значений моды), а для определения медианы необходимо упорядочить ряд и найти средний по порядку элемент (при четном количестве отдельных единиц можно вычислить медиану как полусумму двух средних элементов). Если же данные о значениях признака представлены в виде упорядоченных интервалов его изменения, т.е. интервальных рядов, то расчеты несколько усложняются. Для определения моды в этом случае находится так называемый модальный интервал, т.е. тот интервал, который имеет наибольшую частоту и мода вычисляется по формуле:
где X Мо – нижняя граница модального интервала; h – величина интервала; f Мо – частота, соответствующая модальному интервалу; f Мо-1 – частота предшествующего интервала; f Мо+1 – частота последующего интервала.
Для вычисления медианы в интервальных рядах сначала определяем медианный интервал по данным о накопленных частотах, а затем находим медиану по формуле:
где X Ме – нижняя граница медианного интервала, h – величина интервала; Sf/2 – половина от общего числа наблюдений; S Ме–1 – сумма накопленных частот, предшествующих медианному интервалу; f Ме – частота, соответствующая медианному интервалу.
К структурным средним относятся также следующие величины:
Структурные средние величины



Наиболее часто применяемыми структурными средними величинами являются: мода, медиана, квартили, децили, перцентили.
Все структурные средние являются именованными величинами.
Мода ( 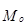
В дискретном вариационном ряду модой является варианта, имеющая наибольшую частоту (частость).
Пример 5.Используя распределение 25 работников по тарифному разряду (цифры условные) рассчитать моду.
Тарифный разряд, 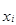 | Число работников, чел., 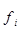 |
| Итого |
Решение. В данном примере наибольшей частоте ( 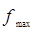
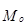
В интервальном вариационном ряду с равными интервалами моду рассчитывают по формуле
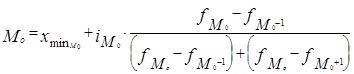
где 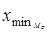
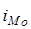
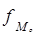
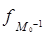
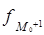
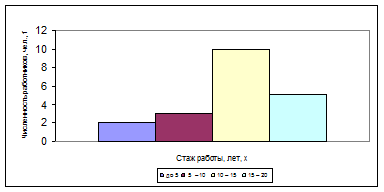
Пример 6. По приведенным условным данным о трудовом стаже 20 работников отдела вычислить моду (по формулам и графически).
| Стаж работы работников, лет | Численность работников, чел. |
| до 5 | |
| 5 –10 | |
| 10–15 | |
| 15–20 | |
| Итого |
Решение. По наибольшей частоте ( 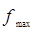
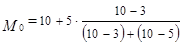
т. е. чаще встречаются работники, имеющие трудовой стаж примерно 13 лет.
В интервальном вариационном ряду моду можно вычислить графически по гистограмме (рис. 4).
В интервальном вариационном ряду с неравными интервалами моду рассчитывают по формуле
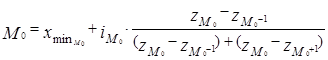
где z – плотности распределения 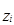
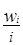
Пример 7. По приведенным условным данным вычислить моду
| Размер заработной платы, руб. / мес. | Численность работников, чел. |
| до 5000 | |
| 5 000–7 000 | |
| 7 000–10 000 | |
| 10 000–15 000 | |
| Итого |
Решение. В данном вариационном ряду интервалы группировки неравные, все предварительные расчеты представим в таблице:
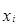 | 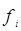 | 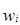 = = 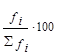 | 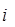 | 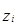 = = 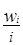 |
| до 5 000 | 2 000 | 0,0065 | ||
| 5 000–7 000 | 2 000 | 0,0200 | ||
| 7 000–10 000 | 3 000 | 0,0090 | ||
| 10 000–15 000 | 5 000 | 0,0040 | ||
| Итого |
Наибольшая плотность распределения 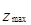
Это означает, что модальным является интервал 5 000 – 7 000 руб.
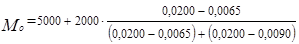
т. е. большинство сотрудников получают заработную плату в размере 6 102 руб. в месяц.
В интервальном вариационном ряду с неравными интервалами моду также можно вычислить графически по гистограмме (по аналогии с ее определением в интервальном вариационном ряду с равными интервалами, только по оси ординат вместо частот (частостей) откладывают соответствующие плотности распределения).
Медиана ( 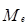
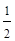
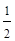
Квартиль (Q)–значение признака, которое делит исходную совокупность на 4 равные по числу единиц части. Например, при вычислении первого квартиля ( 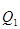
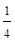
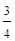
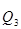
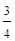
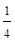

Дециль (D)–значение признака, который делит исходную совокупность на 10 равных частей. Например, при вычислении первого дециля ( 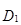
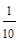
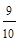
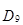
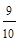
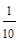
В дискретном вариационном ряду значениями медианы, квартилей и децилей являются варианты, соответствующие единицам совокупности, которые делят исходную совокупность в нужном соотношении.
Пример 8.По исходным данным примера 5 рассчитать медиану, третий квартиль и девятый дециль.
Решение. Вычислим накопленные частоты и определим порядковые номера соответствующих единиц совокупности.
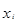 | 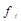 | S |
| Итого | – |
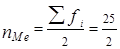
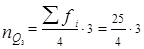
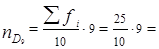
По накопленным частотам определяем, что 12,5-й единице совокупности соответствует значение признака, равное 4, т. е. 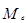
Аналогично определяем, что Q3 = 5 тарифный разряд, т. е. 75% работников имеют 5 тарифный разряд и ниже, а 25% работников – 5 тарифный разряд и выше.
D9 = 6 тарифный разряд, т. е. 90% работников имеют 6 тарифный разряд и ниже, а 10% работников – 6 тарифный разряд.
В интервальном вариационном ряду медиану вычисляют по формуле
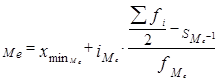
где 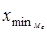
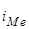
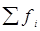
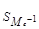
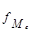
Расчет квартиля и дециля производится аналогично медиане. Например,
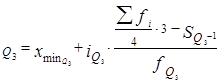
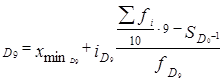
В интервальном вариационном ряду медиану, квартиль, дециль можно вычислить графически по кумуляте.
Пример 9. По исходным данным примера 7 вычислить 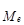
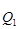
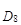
Решение. Рассчитаем накопленные частоты и определим порядковые номера единиц, делящих исходную совокупность в нужном нам соотношении:
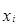 | 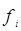 | S |
| до 5 000 | ||
| 5 000–7 000 | ||
| 7 000–10 000 | ||
| 10 000–15 000 | ||
| Итого |
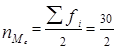
По накопленным частотам определяем, что 15-я единица совокупности содержится в интервале 5 000–7 000 руб. Этот интервал является медианным. Подставим значения в формулу
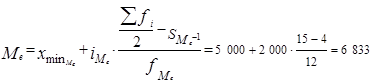
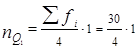
По накопленным частотам определяем, что первый квартиль находится в интервале 5 000 – 7 000 руб. Вычислим первый квартиль
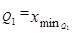
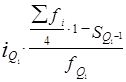
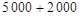
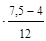
Значит, 25% работников имеют размер заработной платы менее 5 583 руб., а 75% – больше 5 583 руб.