Установить что является событием противоположным событию сегодня первый урок физика

Установить что является событием противоположным событию сегодня первый урок физика

Разработка урока по математике «Вероятность противоположных событий». 11 класс

Учитель: Федорова Ирина Александровна.

Цели: Обучающие: сформулировать понятие противоположного события, рассмотреть и доказать теорему о сумме вероятностей противоположных событий, продолжить формирование умения решать задачи теории вероятностей.

Развивающие: развивать логическое мышление, воображение память.

Воспитательные: воспитывать трудолюбие самостоятельность, аккуратность.

Тип урока: урок изучения новых знаний.

1. Колягин, Ю. М. Алгебра и начала анализа. 11 кл.: Учеб. для общеобразоват. учреждений / Ю. М. Колягин, Ю. В. Сидоров, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин. – 2-е изд. – М.: Мнемозина, 2002.- 240 с.

I. Организационный момент (1-2 ’ ).

II. Актуализация знаний (5-7 ’ ).

III. Введение новых знаний (12-15 ’ ).

IV. Закрепление нового материала (15-20 ’ ).

V. Подведение итогов (1-2 ’ ).

VI. Домашнее задание и его инструктаж (2-3’).

I. Организационный момент (1-2 ’ ).

— Здравствуйте, ребята, садитесь. Кто из учеников отсутствует на уроке? (Воспринимают информацию и отвечают на вопросы).

— Чему равна вероятность появления одного из двух несовместных событий? (Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий, т. е. P(A+B)=P(A)+P(B)).

III. Введение новых знаний (12-15 ’ ).

— А теперь откройте тетради и запишите тему сегодняшнего урока: «Вероятность противоположного события». (Записывают в тетрадях тему урока).

— Запишем определение противоположного события: Событие A’ называется событием, противоположным событию А, если оно происходит, когда не происходит событие А. (Записывают определение под диктовку).

— Пусть теперь в некотором испытании из п элементарных событий, событию A благоприятствуют m1 событий, а событию A’ благоприятствуют m 2 событий, то m 1 + m 2 = п. (Записывают формулу в тетрадях).

— Пример: при бросании игральной кости — 6 элементарных событий ( n=6 ), событию А — «выпало 6 очков» —благоприятствует одно событие ( m1 = 1 ), а событию A’ — «выпало не 6 очков» — благоприятствуют 5 элементарных событий (m 2 = 5): 1 + 5 = 6.

— Сформулируем т еорему: Сумма вероятностей противоположных событий равна 1. (Записывают теорему в тетрадях).

— Сложим вероятности противоположных событий:

— Рассмотрим следующую задачу: Вероятность попадания в мишень стрелком равна 0,6. Какова вероятность того, что он, выстрелив по мишени, промахнется? Пусть событие A — попадание в мишень, чему равна вероятность наступления этого события? (P(A)=0,6). Какое будут противоположное попаданию событие? (Промах). Чему равна вероятность промаха? (P(A’)=1-0,6=0,4).

— Молодцы! Решим следующую задачу: В роте из 100 солдат двое имеют высшее образование. Какова вероятность того, что в случайным образом сформированном взводе из 30 солдат будет хотя бы один человек с высшим образованием? (Записывают условие задачи в тетради).

— Что обозначим за событие A’? (Тогда событие A’ — ни один человек во взводе не имеет высшего образования).

— Сколькими способами можно составить взвод из 30 чел.? (C(30 из 100))

— Сколькими способами можно составить взвод из солдат, не имеющих высшего образования, в составе 30 чел.? (C(30 из 98))

— Тогда чему равна вероятность того, что во взвод попадут только те солдаты, которые не имеют высшего образования?

(P(A’)=C(30 из 98)/С(30 из 100)=(98!/(30!*(98-30)!)/(100!/(30!*(100-30)!)=(98!*30!*70!)/(30!*68!*100!)=(68*70)/(99*100)=161/330).

— Тогда чему равна вероятность того, что во взвод попадет хотя бы один солдат, имеющий высшее образование?

IV. Закрепление нового материала (15-20 ’ ).

— Откройте учебник на стр. 149. Решим № 386 устно: Что является событием, противоположным событию:

1) сегодня первый урок — физика;

2) экзамен сдан на «отлично»;

3) на игральной кости выпало меньше 5 очков;

4) хотя бы одна пуля при трех выстрелах попала в цель?

(Отвечают по очереди: 1) Сегодня первый урок – не физика;

2) Экзамен не сдан на отлично;

3) На игральной кости выпало больше 4 очков;

4) ни одна пуля не попала в цель.

— Молодцы! Дима, иди к доске и реши № 388. Все остальные решают в тетрадях.

(Дима: « Найти вероятность того, что наугад вынутая из полного набора домино (28 костей) одна кость домино не будет «дублем»».

— Лена, реши у доски № 389. Все остальные решают в тетрадях.

(Лена читает: « В ящике лежат 5 белых, 10 черных и 15 красных шаров. Какова вероятность того, что наугад вынутый шар не будет белым? »

Ответ: Вероятность того, что наугад вынутый шар из ящика не будет белым равна 5/6.

V. Подведение итогов (1-2 ’ ).

— На уроке все работали хорошо.

VI. Домашнее задание и его инструктаж (2-3’).

— Откройте дневники и запишите домашнее задание: § 34, №№ 387, 390. (Записывают дом. задание).

— Все эти номера того же вида, задания которого мы выполнили в классе).

Решение домашнего задания.

№ 387. Вероятность выигрыша главного приза равна 10 в (-8) степени. Какова вероятность не выиграть главный приз?

По условию задачи P(A)=10 в (-8) степени, тогда используя теорему о сумме вероятностей противоположных событий: P(A’)=0,9999999.

№ 390. В студенческой группе 22 чел., среди которых 4 девушки. Какова вероятность того, что среди троих случайным образом выбранных из этой группы студентов окажется по крайней мере одна девушка?

Решение: Пусть событие A — выбранный студент – девушка. Тогда событие A’ — выбранный студент – юноша.

22 – 4 = 18 чел. – столько в группе юношей.

Тогда вероятность того, что среди выбранных троих студентов из 22 чел. будет хотя бы одна девушка равна:

Ответ: вероятность того, что среди выбранных троих студентов из 22 чел. будет хотя бы одна девушка равна: 181/385.

Источник

Конспект урока по алгебре «Противоположное событие и его вероятность»(9 класс)

Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа № 38

Конспект урока по алгебре « Теория вероятностей и статистика» в 9 классе:

«Противоположное событие и его вероятность»

Учитель: Стародымова Г.Д.

Тема урока: Противоположное событие и его вероятность.

C оздание условий для овладения учащимися системой математических знаний и умений, необходимых для применения в практической деятельности, при изучении смежных дисциплин, продолжения образования .

Развивающая : способствовать формированию метапредметных умений, развивать познавательные процессы, память, воображение, наблюдательность, расширение кругозора.

Воспитательная : воспитание ответственного отношения к труду, воли и настойчивости в достижении конечных результатов, ответственного отношения к коллективной деятельности, умения оценивать свою работу и работу товарищей; воспитание культуры математической речи.

Оборудование: интерактивная доска, проектор, оценочный лист.

1.Организационный момент. Приветствие, проверка готовности учащихся к уроку.

— Здравствуйте, дети! Садитесь. Запишите в тетрадях число, классная работа.

Постановка целей и задач урока.

— Мы продолжаем изучать тему « Теория вероятностей и статистика ».

« Теория-это, когда все известно, но ничего не работает . Практика-это, когда все работает , но никто не знает почему. Мы объединяем теорию и практику: ничего не работает…и никто не знает почему!»

(Например, сколько нужно запасти порций рыбы и курицы в самолет, чтобы практически наверняка не было недовольных пассажиров?)

Я надеюсь, что вы вскоре приведете еще больше примеров задач, которые можно решить с помощью теории вероятностей.

2.Актуализация опорных знаний.

Какими можно назвать события «выигрыш» и «не выигрыш» в лотерее?

(обратными событиями, противоположными событиями ).

Приведите примеры других противоположных событий:

— студент сдаст зачет и что он его не сдаст;

— попадание и промах при выстреле;

— выпадение орла и решки при одном броске;

— отказ прибора в данном интервале времени и его исправная работа.

Решите задачу: на школьном вечере среди 100 присутствующих были распространены лотерейные билеты (каждому достался один билет), среди которых 5 выигрышных. Какова вероятность, что конкретному школьнику достался выигрышный билет? (Ответ: р=5/100=0,05) Какова вероятность, что конкретному школьнику достался невыигрышный билет? (Ответ: невыигрышных билетов 100-5=95, тогда вероятность равна 95/100=0,95)

Бросают две монеты. Чему равна вероятность появления хотя бы одного герба?

Решая эту задачу по известной схеме учащиеся приходят к выводу, что формула Р(С) = P(A) +P(B) не применима, т. к. события в этом испытании совместны. Для решения в сложившийся ситуации я рекомендую предложить учащимся избрать другой путь решения, а именно:

2) найти вероятность этого события Р(Ā) = 1/4.

-Какова же связь между вероятностями противоположных событий?

(сумма вероятности двух противоположных событий равна единице)

Сумма вероятностей противоположных событий равна 1:

Решим задачу: Вероятность того, что день будет дождливым, равна 0,7. Найдите вероятность того, что день будет ясным.

( События «день дождливый» и «день ясный» — противоположные, поэтому искомая вероятность 1 — 0,7 = 0,3)

С целью формирования нового понятия предлагаю решить задачи, для первой задачи прежде составить алгоритм решения:

Задача 1. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,05. Покупатель в магазине выбирает одну ручку. Найдите вероятность того, что эта ручка пишет хорошо.

1.Определим событие А – выбранная ручка пишет хорошо.

2.Противоположное событие .

3.Вероятность противоположного события Р( )=0,05.

4. Применяя формулу вероятности противоположных событий, получаем ответ: Р(А)=1-Р( )=1-0,05=0,95.

Задача 2. В магазине стоят два платежных автомата. Оба могут быть неисправны с вероятностью 0,0025. Найдите вероятность того, что хотя бы один автомат исправен.

Событие — исправны оба автомата. Тогда противоположное событие означает исправность хотя бы одного автомата. Следовательно,

Задача 3. При изготовлении подшипников диаметром 55 мм вероятность того, что диаметр будет отличаться от заданного не более чем на 0,01 мм, равна 0,925. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 54,99, или больше, чем 55,01 мм.

Обозначим через событие «диаметр подшипника отличается от заданного более, чем на 0,01 мм». Тогда — искомая величина. В условии нам дана вероятность противоположного события . Тогда

.

Учащиеся получают 1 балл за каждую верно решенную задачу, за составленный алгоритм – 1 балл.

Физкультминутка. Проводит физорг класса.

Задача: Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.

(Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,8 2 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128).

— Проверьте решение по образцу(слайд), исправьте допущенные ошибки, окажите взаимопомощь товарищу.

(Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,8 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128)

Учащиеся, справившиеся с заданием, получают 2 балла.

1 . Отметь событие, являющееся противоположным событию:

Выпало одно из чисел: 1,2,3,4,5,6

Выпало одно из чисел: 1,2,3,4,6

2. Выясни, является ли следующее высказывание истинным:

(Ответ запиши в виде десятичной дроби)

4. В ящике лежат 5 белых, 10 черных и 15 красных шаров. Какова вероятность того, что наугад вынутый шар не будет белым?»

(Ответ запиши в виде десятичной дроби, дробь округлите до сотых)

3. Подведение итогов. Рефлексия.

— Какой ответ вы дадите после этого урока?

— Я надеюсь, что сегодняшний урок будет для вас еще одним аргументом в пользу изучения теории вероятностей.

— Оцените свою деятельность в оценочном листе, отметьте в листе свое настроение.

4. Домашнее задание. Инструктаж по его выполнению.

— Составьте кроссворд с математическими терминами из темы «Вероятность». На следующем занятии мы разгадаем самые интересные кроссворды.

4 и меньше баллов – подойти к учителю для консультации.

Источник

Урок-лекция для 8-го класса «Вероятности случайных событий»

Разделы: Математика

Цель: ознакомить учащихся с правилами сложения и умножения вероятностей, понятием противоположных событий на кругах Эйлера.

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по иному.

Приведём примеры случайных событий: бросаются игральные кости, бросается монета, проводится стрельба по мишени и т.д.

Все приведённые примеры можно рассматривать под одним и тем же углом зрения: случайные вариации, неодинаковые результаты ряда опытов, основные условия которых остаются неизменными.

Совершенно очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной степени элементы случайности. Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали.

Случайные отклонения неизбежно сопутствуют любому закономерному явлению. Тем не менее, в ряде практических задач этими случайными элементами можно пренебречь, рассматривая вместо реального явления, его упрощённую схему «модель» и предполагая, что в данных условиях опыта явление протекает вполне определённым образом.

Однако существует ряд задач, где интересующий нас исход опыта зависит от столь большого числа факторов, что практически невозможно зарегистрировать и учесть все эти факторы.

Случайные события можно различным способом сочетать друг с другом. При этом образуются новые случайные события.

Для наглядного изображения событий используют диаграммы Эйлера. На каждой такой диаграмме прямоугольником изображают множество всех элементарных событий (рис.1). Все другие события изображают внутри прямоугольника в виде некоторой его части, ограниченной замкнутой линией. Обычно такие события изображают окружности или овалы внутри прямоугольника.

Рассмотрим наиболее важные свойства событий с помощью диаграмм Эйлера.

Объединением событий A и B называют событие C, состоящее из элементарных событий принадлежащих событию А или В (иногда объединения называют суммой).

Результат объединения можно изобразить графически диаграммой Эйлера (рис. 2).

Пересечением событий А и В называют событие С, которое благоприятствует и событию А, и событию В (иногда пересечения называют произведением).

Результат пересечения можно изобразить графически диаграммой Эйлера (рис. 3).

Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и то же опыта. Такие события называют несовместными, а их пересечение – пустое событие.

Разностью событий А и В называют событие С, состоящее из элементарных событий А, которые не являются элементарными событиями В.

Результат разности можно изобразить графически диаграммой Эйлера (рис.4)

Пусть прямоугольник изображает все элементарные события. Событие А изобразим в виде круга внутри прямоугольника. Оставшаяся часть прямоугольника изображает противоположное событию A, событие (рис.5)

Событием, противоположным событию А называют событие, которому благоприятствуют все элементарные события, не благоприятствующие событию А.

Событие, противоположное событию А, принято обозначать .

Примеры противоположных событий.

Объединением нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Например, если опыт состоит в пяти выстрелах по мишени и даны события:

А0- ни одного попадания;
А1- ровно одно попадание;
А2- ровно 2 попадания;
А3- ровно 3 попадания;
А4- ровно 4 попадания;
А5- ровно 5 попаданий.

Найти события: не более двух попаданий и не менее трёх попаданий.

Решение: А=А0+А1+А2 – не более двух попаданий;

В=А3+А4+А5 – не менее трёх попаданий.

Пересечением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Например, если по мишени производится три выстрела, и рассматриваются события:

то событие состоит в том, что в мишень не будет ни одного попадания.

При определении вероятностей часто приходится представлять сложные события в виде комбинаций более простых событий, при­меняя и объединение, и пересечение событий.

Например, пусть по мишени производится три выстрела, и рассматриваются следующие элементарные события:

— попадание при первом выстреле,
— промах при первом выстреле,
— попадание при втором выстреле,
— промах при втором выстреле,
— попадание при третьем выстреле,
— промах при третьем выстреле.

Рассмотрим более сложное событие В, состоящее в том, что в результате данных трёх выстрелов будет ровно одно попада­ние в мишень. Событие В можно представить в виде следующей комбинации элементарных событий:

Событие С, состоящее в том, что в мишень будет не менее двух попаданий, может быть представлено в виде:

На рис.6.1 и 6.2 показано объединение и пересечение трёх событий.

рис.6

Для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные. Позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Применяя эти косвенные методы, мы всегда в той или иной форме пользуемся основными правилами теории вероятностей. Этих правил два: правило сложения вероятностей и правило умножения вероятностей.

Правило сложения вероятностей формулируется следующим образом.

Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий:

Сумма вероятностей противоположных событий равна единице:

Р(А) + Р()= 1.

На практике весьма часто оказывается легче вычислить вероятность противоположного события А, чем вероятность прямого события А. В этих случаях вычисляют Р (А) и находят

Р (А) = 1-Р().

Рассмотрим несколько примеров на применение правила сложения.

Решение. Рассмотрим события:

Очевидно, А= А1 +А2+А3.

По правилу сложения вероятностей:

Р (А) = Р (А1) + Р (А2) + Р (А3) = 0,050 + 0,010 + 0,001 = 0,061.

Решение. Рассмотрим события:

Очевидно, А = А1 + А2 + А3.

Так как при сбрасывании одной бомбы события Al, А2, А3 несовместны, то

Р (А) = Р (A1) + Р(А2) +Р(А3) == 0,01 + 0,008 + 0,025 = 0,043.

Пример 3. Круговая мишень состоит из трёх зон: I, II и III. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. Найти вероятность промаха.

Тогда =А1+ А2 + А3,

Р() = Р (A1) + Р (А2) + Р (А3) = 0,15 + 0,23 + 0,17 = 0,55,

Р(А) = 1- Р() = 0,45.

Источник

Вопросы

Что является событием 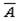, противоположным событию А?

Событие А	Событие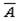
Сегодня первый урок — физика	Сегодня первый урок – не физика
Экзамен сдан на «отлично»	Экзамен не сдан на «отлично»
На игральной кости выпало меньше 5 очков	На игральной кости выпало больше 4 очков
Хотя бы одна пуля при трех выстрелах попала в цель	Ни одна пуля не попала в цель

Эта тема принадлежит разделу:

Основы теории вероятностей

Тема вероятности сложных событий.. лекция противоположное событие вероятность противоположного события.. независимые события..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Вопросы

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Противоположное событие
Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать

Вероятность противоположного события
Теорема. Сумма вероятностей противоположных событий равна единице:

Произведение событий
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно.

Сумма событий
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает, по крайней мере, одно из событий: А или В

Доказательство
Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В

Доказательство
Рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, А, В и С, равносильно наступлению одного из двух событий, A + В и С, поэт

Условная вероятность
Ранее случайное событие определено как событие, которое при осуществлении совокупности условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений

Теорема умножения вероятностей
Рассмотрим два события: А и В. Пусть вероятности Р(А) и РA(В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ

Доказательство
По определению условной вероятности, РA(B) = Р(АВ) / Р(A). Отсюда Р (АВ) = Р(А) РA (В). Замечание. Применив формулу (1) к

Теорема умножения для независимых событий
Для независимых событий теорема умножения Р(АВ) = Р(А) ·РA(В) имеет вид Р(АВ) = Р(А) ·Р (В), (5) т. е. вероятность совместного появления двух

Доказательство
Рассмотрим три события: А, В и С. Совмещение событий А, В и С равносильно совмещению событий АВ и С, поэтому Р(AВС) = Р (АВ·С). Так как события А, В и С независимы в совокупности,

Вероятность появления хотя бы одного события
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из со

Задачи для самостоятельного решения
Задача 26.Вероятность того, что стрелок при одном выстреле попадает в мишень, равна р = 0,9. Стрелок произвел 3 выстрела. Найти вероятность того, что все 3 выстрела

Вероятность суммы совместимых событий
Теорема. Вероятность суммы двух совместимых событий А и В равна сумме вероятностей этих событий минус вероятность их произведения:

Формула полной вероятности
Если событие А может произойти только при выполнении одного из событий

Источник