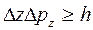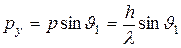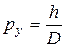Утверждение что произведение неопределенностей координаты и соответствующей ей проекции

Соотношение неопределенностей

В классической механике всякая частица движется по определенной тра­ектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микрочастицы из-за наличия у них волновых свойств существен­но отличаются от классических частиц. Одно из основных различий заключа­ется в том, что нельзя говорить о движении микрочастицы по определенной траттории и неправомерно говорить об одновременных точных значениях ее координаты и импульса. Это следует из корпускулярно-волнового дуализма. Так, понятие «длина волны в данной точке» лишено физического смысла, а поскольку импульс выражается через длину волны, то отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. И наоборот, если микрочастица находится в состоянии с точным значением координаты, то ее импульс является полностью неопределенным.

В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения вих поведении, пришел в 1927 г. к вы­воду, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, р_у, p_z), причем неопределенности этих величин удовлетворяют условиям

(224)

т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Следует отметить, что неравенство (224) не является точным. В литературе часто приводится формула . Она аналогична (224), но в её правой части стоит — постоянная Планка «с чертой», называемая приведённой постоянной Планка. Между двумя этими формами записи нет противоречия: они обе справедливы только по порядку величины и обе годятся для качественных оценок. Более точное выражение имеет вид:

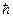
Здесь скобки обозначают дисперсию A.

В справочнике по физике это соотношение неопределенностей дается виде:

(225)

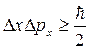
Из соотношения неопределенностей (225) следует, что, например, если мик­рочастица находится в состоянии с точным значением координаты (Dх = 0), то в этом состоянии соответствующая проекция ее импульса оказывается со­вершенно неопределенной (Dр —>¥), и наоборот. Таким образом, для микро­частицы не существует состояний, в которых ее координаты и импульс име­ли бы одновременно точные значения. Отсюда вытекает и фактическая не­возможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта.

Принцип неопределённости не просто налагает ограничения на возможные результаты измерений. Он имеет более глубокий смысл и вскрывает новые для нас внутренние свойства самого объекта микромира: электрон не может одновременно иметь определённые значения проекций импульса и координаты на одно направление. Это заключение справедливо, конечно, не только для электрона, но и для любой частицы, локализованной в атомных масштабах (порядка ангстрема) и масса которой сравнима с массой атома.

В квантовой теории рассматривается также соотношение неопределенностей для энергии W и времени t. Неопределенности этих величин удовлетворяют условию:

(226)

где — неопределенность энергии некоторого состояния системы, -промежуток времени, в течение которого оно существует. Система. Имеющая среднее время жизни , не может быть охарактеризована определенным значением энергии; разброс энергии возрастает с уменьшением среднего времени жизни. Из соотношения (226) также следует, что частота излучаемого фотона также должна иметь неопределенность , т.е. линии спектра должны характеризоваться частотой .

Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.

Дифракционные явления проявляются наиболее отчетливо, когда размеры препятствия, на котором происходит дифракция волн, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.

Рассмотрим, например, дифракцию электронов на одиночной щели ширины D (рисунок 77). На графике справа приведено распределение электронов на фотопластинке. Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ₁ этого максимума находится из условия

Это формула соответствует волновой теории.

С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение p_y поперечного импульса равно

где p – модуль полного импульса электрона, равный, согласно де Бройлю, h / λ. Величина p при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ. Из этих соотношений следует

Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δy = D. Величину Δy называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна p_y или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δp_y. Таким образом, величины Δy и Δp_y связаны соотношением

которое называется соотношением неопределенностей Гейзенберга. Величины Δy и Δp_y нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой двигался какой-то конкретный электрон после прохождения щели и до фотопластинки в рассмотренном мысленном эксперименте.

Рассмотрим еще один мысленный эксперимент – дифракцию электронного пучка на двух щелях (рис. 78). Схема этого эксперимента совпадает со схемой оптического интерференционного опыта Юнга.

Рисунок 78

Анализ этого эксперимента позволяет проиллюстрировать логические трудности, возникающие в квантовой теории. Те же проблемы возникают при объяснении оптического опыта Юнга, исходя из концепции фотонов.

Если в опыте по наблюдению дифракции электронов на двух щелях закрыть одну из щелей, то интерференционные полосы исчезнут, и фотопластинка зарегистрирует распределение электронов, продифрагировавших на одной щели (рисунок 77). В этом случае все электроны, долетающие до фотопластинки, проходят через единственную открытую щель. Если же открыты обе щели, то появляются интерференционные полосы, и тогда возникает вопрос, через какую из щелей пролетает тот или иной электрон?

Психологически очень трудно смириться с тем, что ответ на этот вопрос может быть только один: электрон пролетает через обе щели. Мы интуитивно представляем себе поток микрочастиц как направленное движение маленьких шариков и применяем для описания этого движения законы классической физики. Но электрон (и любая другая микрочастица) обладает не только корпускулярными, но и волновыми свойствами. Легко представить, как электромагнитная световая волна проходит через две щели в оптическом опыте Юнга, т. к. волна не локализована в пространстве. Но если принять концепцию фотонов, то мы должны признать, что каждый фотон тоже не локализован. Невозможно указать, через какую из щелей пролетел фотон, как невозможно проследить за траекторией движения фотона до фотопластинки и указать точку, в которую он попадет. Опыт показывает, что даже в том случае, когда фотоны пролетают через интерферометр поштучно, интерференционная картина после пролета многих независимых фотонов все равно возникает. Поэтому в квантовой физике делается вывод: фотон интерферирует сам с собой.

Все вышесказанное относится и к опыту по дифракции электронов на двух щелях. Вся совокупность известных экспериментальных фактов может найти объяснение, если принять, что дебройлевская волна каждого отдельного электрона проходит одновременно через оба отверстия, в результате чего и возникает интерференция. Поштучный поток электронов тоже дает интерференцию при длительной экспозиции, т. е. электрон, как и фотон, интерферирует сам с собой.

Поясним, что соотношение неопределенностей действительно вытекает из волновых свойств микрочас­тиц. Пусть поток электронов проходит через узкую щель шириной Dх, расположенную перпендикулярно направлению их движения (рис.77). Так как электроны обладают волновыми свойствами, то при их прохож­дении через щель, размер которой сравним с длиной волны де Бройля электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране (Э), характеризуется главным максимумом, расположен­ным симметрично оси Y, и побочными максимумами по обе стороны от главного (их не рассматриваем, так как основная доля интенсивности приходится на главный максимум).

Источник

Принцип неопределенности Гейзенберга

Невозможно одновременно с точностью определить координаты и скорость квантовой частицы.

В обыденной жизни нас окружают материальные объекты, размеры которых сопоставимы с нами: машины, дома, песчинки и т. д. Наши интуитивные представления об устройстве мира формируются в результате повседневного наблюдения за поведением таких объектов. Поскольку все мы имеем за плечами прожитую жизнь, накопленный за ее годы опыт подсказывает нам, что раз всё наблюдаемое нами раз за разом ведет себя определенным образом, значит и во всей Вселенной, во всех масштабах материальные объекты должны вести себя аналогичным образом. И когда выясняется, что где-то что-то не подчиняется привычным правилам и противоречит нашим интуитивным понятиям о мире, нас это не просто удивляет, а шокирует.

В первой четверти ХХ века именно такова была реакция физиков, когда они стали исследовать поведение материи на атомном и субатомном уровнях. Появление и бурное развитие квантовой механики открыло перед нами целый мир, системное устройство которого попросту не укладывается в рамки здравого смысла и полностью противоречит нашим интуитивным представлениям. Но нужно помнить, что наша интуиция основана на опыте поведения обычных предметов соизмеримых с нами масштабов, а квантовая механика описывает вещи, которые происходят на микроскопическом и невидимом для нас уровне, — ни один человек никогда напрямую с ними не сталкивался. Если забыть об этом, мы неизбежно придем в состояние полного замешательства и недоумения. Для себя я сформулировал следующий подход к квантово-механическим эффектам: как только «внутренний голос» начинает твердить «такого не может быть!», нужно спросить себя: «А почему бы и нет? Откуда мне знать, как всё на самом деле устроено внутри атома? Разве я сам туда заглядывал?» Настроив себя подобным образом, вам будет проще воспринять статьи этой книги, посвященные квантовой механике.

Принцип Гейзенберга вообще играет в квантовой механике ключевую роль хотя бы потому, что достаточно наглядно объясняет, как и почему микромир отличается от знакомого нам материального мира. Чтобы понять этот принцип, задумайтесь для начала о том, что значит «измерить» какую бы то ни было величину. Чтобы отыскать, например, эту книгу, вы, войдя в комнату, окидываете ее взглядом, пока он не остановится на ней. На языке физики это означает, что вы провели визуальное измерение (нашли взглядом книгу) и получили результат — зафиксировали ее пространственные координаты (определили местоположение книги в комнате). На самом деле процесс измерения происходит гораздо сложнее: источник света (Солнце или лампа, например) испускает лучи, которые, пройдя некий путь в пространстве, взаимодействуют с книгой, отражаются от ее поверхности, после чего часть из них доходит до ваших глаз, проходя через хрусталик, фокусируется, попадает на сетчатку — и вы видите образ книги и определяете ее положение в пространстве. Ключ к измерению здесь — взаимодействие между светом и книгой. Так и при любом измерении, представьте себе, инструмент измерения (в данном случае, это свет) вступает во взаимодействие с объектом измерения (в данном случае, это книга).

В классической физике, построенной на ньютоновских принципах и применимой к объектам нашего обычного мира, мы привыкли игнорировать тот факт, что инструмент измерения, вступая во взаимодействие с объектом измерения, воздействует на него и изменяет его свойства, включая, собственно, измеряемые величины. Включая свет в комнате, чтобы найти книгу, вы даже не задумываетесь о том, что под воздействием возникшего давления световых лучей книга может сдвинуться со своего места, и вы узнаете ее искаженные под влиянием включенного вами света пространственные координаты. Интуиция подсказывает нам (и, в данном случае, совершенно правильно), что акт измерения не влияет на измеряемые свойства объекта измерения. А теперь задумайтесь о процессах, происходящих на субатомном уровне. Допустим, мне нужно зафиксировать пространственное местонахождение электрона. Мне по-прежнему нужен измерительный инструмент, который вступит во взаимодействие с электроном и возвратит моим детекторам сигнал с информацией о его местопребывании. И тут же возникает сложность: иных инструментов взаимодействия с электроном для определения его положения в пространстве, кроме других элементарных частиц, у меня нет. И, если предположение о том, что свет, вступая во взаимодействие с книгой, на ее пространственных координатах не сказывается, относительно взаимодействия измеряемого электрона с другим электроном или фотонами такого сказать нельзя.

В начале 1920-х годов, когда произошел бурный всплеск творческой мысли, приведший к созданию квантовой механики, эту проблему первым осознал молодой немецкий физик-теоретик Вернер Гейзенберг. Начав со сложных математических формул, описывающих мир на субатомном уровне, он постепенно пришел к удивительной по простоте формуле, дающий общее описание эффекта воздействия инструментов измерения на измеряемые объекты микромира, о котором мы только что говорили. В результате им был сформулирован принцип неопределенности, названный теперь его именем:

математическое выражение которого называется соотношением неопределенностей Гейзенберга:

где Δx — неопределенность (погрешность измерения) пространственной координаты микрочастицы, Δv — неопределенность скорости частицы, m — масса частицы, а h — постоянная Планка, названная так в честь немецкого физика Макса Планка, еще одного из основоположников квантовой механики. Постоянная Планка равняется примерно 6,626 x Дж·с, то есть содержит 33 нуля до первой значимой цифры после запятой.

Термин «неопределенность пространственной координаты» как раз и означает, что мы не знаем точного местоположения частицы. Например, если вы используете глобальную систему рекогносцировки GPS, чтобы определить местоположение этой книги, система вычислит их с точностью до 2-3 метров. (GPS, Global Positioning System — навигационная система, в которой задействованы 24 искусственных спутника Земли. Если у вас, например, на автомобиле установлен приемник GPS, то, принимая сигналы от этих спутников и сопоставляя время их задержки, система определяет ваши географические координаты на Земле с точностью до угловой секунды.) Однако, с точки зрения измерения, проведенного инструментом GPS, книга может с некоторой вероятностью находиться где угодно в пределах указанных системой нескольких квадратных метров. В таком случае мы и говорим о неопределенности пространственных координат объекта (в данном примере, книги). Ситуацию можно улучшить, если взять вместо GPS рулетку — в этом случае мы сможем утверждать, что книга находится, например, в 4 м 11 см от одной стены и в 1м 44 см от другой. Но и здесь мы ограничены в точности измерения минимальным делением шкалы рулетки (пусть это будет даже миллиметр) и погрешностями измерения и самого прибора, — и в самом лучшем случае нам удастся определить пространственное положение объекта с точностью до минимального деления шкалы. Чем более точный прибор мы будем использовать, тем точнее будут полученные нами результаты, тем ниже будет погрешность измерения и тем меньше будет неопределенность. В принципе, в нашем обыденном мире свести неопределенность к нулю и определить точные координаты книги можно.

И тут мы подходим к самому принципиальному отличию микромира от нашего повседневного физического мира. В обычном мире, измеряя положение и скорость тела в пространстве, мы на него практически не воздействуем. Таким образом, в идеале мы можем одновременно измерить и скорость, и координаты объекта абсолютно точно (иными словами, с нулевой неопределенностью).

В мире квантовых явлений, однако, любое измерение воздействует на систему. Сам факт проведения нами измерения, например, местоположения частицы, приводит к изменению ее скорости, причем непредсказуемому (и наоборот). Вот почему в правой части соотношения Гейзенберга стоит не нулевая, а положительная величина. Чем меньше неопределенность в отношении одной переменной (например, Δx), тем более неопределенной становится другая переменная (Δv), поскольку произведение двух погрешностей в левой части соотношения не может быть меньше константы в правой его части. На самом деле, если нам удастся с нулевой погрешностью (абсолютно точно) определить одну из измеряемых величин, неопределенность другой величины будет равняться бесконечности, и о ней мы не будем знать вообще ничего. Иными словами, если бы нам удалось абсолютно точно установить координаты квантовой частицы, о ее скорости мы не имели бы ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы понятия не имели, где она находится. На практике, конечно, физикам-экспериментаторам всегда приходится искать какой-то компромисс между двумя этими крайностями и подбирать методы измерения, позволяющие с разумной погрешностью судить и о скорости, и о пространственном положении частиц.

На самом деле, принцип неопределенности связывает не только пространственные координаты и скорость — на этом примере он просто проявляется нагляднее всего; в равной мере неопределенность связывает и другие пары взаимно увязанных характеристик микрочастиц. Путем аналогичных рассуждений мы приходим к выводу о невозможности безошибочно измерить энергию квантовой системы и определить момент времени, в который она обладает этой энергией. То есть, если мы проводим измерение состояния квантовой системы на предмет определения ее энергии, это измерение займет некоторый отрезок времени — назовем его Δt. За этот промежуток времени энергия системы случайным образом меняется — происходят ее флуктуация, — и выявить ее мы не можем. Обозначим погрешность измерения энергии Δ Е. Путем рассуждений, аналогичных вышеприведенным, мы придем к аналогичному соотношению для Δ Е и неопределенности времени, которым квантовая частица этой энергией обладала:

Относительно принципа неопределенности нужно сделать еще два важных замечания:

он не подразумевает, что какую-либо одну из двух характеристик частицы — пространственное местоположение или скорость — нельзя измерить сколь угодно точно;

принцип неопределенности действует объективно и не зависит от присутствия разумного субъекта, проводящего измерения.

Иногда вам могут встретиться утверждения, будто принцип неопределенности подразумевает, что у квантовых частиц отсутствуют определенные пространственные координаты и скорости, или что эти величины абсолютно непознаваемы. Не верьте: как мы только что видели, принцип неопределенности не мешает нам с любой желаемой точностью измерить каждую из этих величин. Он утверждает лишь, что мы не в состоянии достоверно узнать и то, и другое одновременно. И, как и во многом другом, мы вынуждены идти на компромисс. Опять же, писатели-антропософы из числа сторонников концепции «Новой эры» иногда утверждают, что, якобы, поскольку измерения подразумевают присутствие разумного наблюдателя, то, значит, на некоем фундаментальном уровне человеческое сознание связано с Вселенским разумом, и именно эта связь обусловливает принцип неопределенности. Повторим по этому поводу еще раз: ключевым в соотношении Гейзенберга является взаимодействие между частицей-объектом измерения и инструментом измерения, влияющим на его результаты. А тот факт, что при этом присутствует разумный наблюдатель в лице ученого, отношения к делу не имеет; инструмент измерения в любом случае влияет на его результаты, присутствует при этом разумное существо или нет.

Источник

Гипотеза Де Бройля. Соотношение неопределенностей Гейзенберга.

Французский ученый Луи де Бройль, осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновой природе света, выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия Е и импульс р, а с другой – волновые характеристики – частота n и длина волны l. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

. (1)

Смелость гипотезы де Бройля заключалась именно в том, что соотношение (1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:

. (2)

Это соотношение справедливо для любой частицы с импульсом р.

Определим некоторые основные свойства волн де Бройля. Рассмотрим свободно движущуюся со скоростью v частицу массой m. Вычислим для нее фазовую и групповую скорости волн де Бройля. Итак, фазовая скорость:

, (3)

где и , – волновое число. Так как c>v, то фазовая скорость волн де Бройля больше скорости света в вакууме.

Групповая скорость : .

Для свободной частицы, согласно теории относительности Эйнштейна, справедливо , тогда

.

Следовательно, групповая скорость волн де Бройля равна скорости частицы.

Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства частиц и все свойства волн нельзя. Значит, необходимо внести некоторые ограничения в применении к объектам микромира понятий классической механики.

В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (x, y, z), и определенную соответствующую проекцию импульса (p_x, p_y, p_z), причем неопределенности этих величин удовлетворяют условиям

, , , (4)

т.е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Из соотношения неопределенностей (4) следует, что, например, если микрочастица находится в состоянии с точным значением координаты (Dx=0), то в этом состоянии (Dp_x®¥), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.

В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t, т.е. неопределенности этих величин удовлетворяют условию

. (5)

Подчеркнем, что DЕ – неопределенность энергии некоторого состояния системы, Dt – промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни Dt, не может быть охарактеризована определенным значением энергии; разброс энергии возрастает с уменьшением среднего времени жизни. Из выражения (5) следует, что частота излученного фотона также должна иметь неопределенность , т.е. линии спектра должны характеризоваться частотой, равной . Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.

43.уравнение шредингера для стационарных состояний

Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шрёдингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы.

Общее уравнение Шредингера имеет вид:

, (1)

где h = h / (2π), m – масса частицы, Δ – оператор Лапласа , i – мнимая единица, U(x, y, z, t) – потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x, y, z, t) – искомая волновая функция частицы.

Уравнение (1) справедливо для любой частицы (со спином, равным 0), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью υ«с.

Оно дополняется условиями, накладываемыми на волновую функцию:

1) волновая функция должна быть конечной, однозначной и непрерывной;

2) производные должны быть непрерывны;

3) функция |Ψ| 2 должна быть интегрируема (это условие в простейших случаях сводится к условию нормировки вероятностей ).

Уравнение (1) называют уравнением Шредингера, зависящим от времени.

Дли многих физических явлений, происходящих в микромире, уравнение (1) можно упростить, исключив зависимость Ψ от времени, т.е. найти уравнение Шредингера для стационарных состояний – состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функция U = U (х, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде

. (2)

Уравнение (2) называется уравнением Шредингера для стационарных состояний.

В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: вол новые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными.

Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями Ψ. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными.Решения, которые соответствуют собственным значениям энергии, называются собственнымифункциями.Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором – о дискретном спектре.

Источник