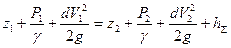зависимость чего показывает диаграмма бернулли

Диаграмма уравнения Бернулли

Диаграмма уравнения Бернулли является графическим представлением изменения различных слагаемых уравнения Бернулли по длине трубопровода. Диаграмма характеризует удельную механическую энергию потока и включает в себя три линии: линию полного напора, пьезометрическую линию и линию геометрического напора.

Линия полного напора характеризует полную удельную механическую энергию, то есть сумму кинетической и потенциальной энергий:

,

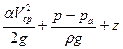
при этом удельная потенциальная энергия давления 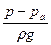при построении диаграммы определяется не абсолютным давлением, а избыточным.

Пьезометрическая линия характеризует удельную потенциальную энергию потока и представляет сумму двух слагаемых

.

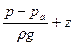
Геометрическая линия, или линия геометрического напора характеризует уклон трубопровода, т. е. изменение координаты z оси трубопровода.

На рис.47 приведена диаграмма Бернулли для трубы переменного сечения. В первом сечении (1-1) полная удельная механическая энергия характеризуется величиной О₁А₁. По мере движения жидкости в трубе ее энергия расходуется, вследствие чего линия полного напора А₁А₂ всегда понижается. Если бы жидкость была невязкой, то полная удельная механическая энергия потока не менялась бы (линия А₁В) из-за отсутствия потерь. Расстояние между линиями полного напора А₁А₂ и пьезометрической С₁С₂ равно 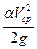и увеличивается по потоку, так как сечение трубы уменьшается, а это приводит к увеличению средней скорости и, следовательно, кинетической энергии. В сечении 2-2 полная удельная механическая энергия потока характеризуется величиной О₂А₂ и она меньше, чем полная энергия в сечении 1-1 на величину потерь h (А₂В).

Показанная на диаграмме Бернулли линия геометрических напоров D₁D₂ характеризует изменение удельной потенциальной энергии положения z, являясь, по существу осью трубопровода.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Диаграмма уравнения Бернулли

Диаграмма уравнения Бернулли представляет собой геометрическую интерпретацию, которая в графическом виде отображает изменения удельной энергии потока, то есть энергии, отнесенной к единице веса жидкости.

Диаграмма уравнения Бернулли состоит из пьезометрической линии P-P, отображающей изменение удельной потенциальной энергии и гидродинамической линии Е-Е, отображающей изменение удельной механической энергии.

Для двух любых контрольных сечений потока уравнение Бернулли записывается

Пьезометрическая линия расположена от плоскости сравнения 0-0 на расстоянии Z +P/γ;

Гидродинамическая линия расположена от плоскости0-0 на расстоянии Z+P/γ + £V 2 /2g

Величина Н= Z+ P/γ+ £V 2 /2g называется гидродинамическим напором.

Гидродинамическая линия имеет уклон вдоль потока, который называется гидродинамическим уклоном. Уклон пьезометрической линии, называется пьезометрическим уклоном.

Пьезометрическая и гидродинамическая линия на участках местных сопротивлений условно изображаются вертикальным уступом.

Высота уступа гидродинамической линии графически изображает местную потерю напора h_m, то есть ту часть энергии, которая вследствие местных сил трения обращается во внутреннюю, тепловую энергию и поэтому считается потерянной.

Источник

Зависимость чего показывает диаграмма бернулли

Уравнение Бернулли для реальной и идеальной жидкости

Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.

График Бернулли и уравнение Бернулли для идеальной жидкости:

График Бернулли и уравнение Бернулли для реальной жидкости:

Смысл уравнения Бернулли

Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.

Назначение уравнения Бернули

Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.

Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации

Задача. Пример решения уравнения Бернулли

По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.

Как понять уравнение Бернулли?

Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве

Точка 1 – это место где известно давление

Точка 2 – это место где нужно узнать давление

Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)

То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.

Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)

Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.

Сборка формулы уравнения Бернулли

Как избавится от минуса?

Как избавится от множителя (-1)?

Что такое идеальная жидкость?

Формула Бернулли для реальной жидкости

Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.

Потому что реальная жидкость движется не равномерно

У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.

Формула коэффициента Кориолиса

Что такое коэффициент Кориолиса?

Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.

Чему равен коэффициент Кориолиса?

Нд.п. – Это динамические потери. Это потери вызванные движением воды.

Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:

Посмотрите видеоурок по составлению уравнения Бернулли:

Как сделать гидравлический расчет погружного насоса?

Источник

Диаграмма уравнения Бернулли

Диаграмма уравнения Бернулли является графическим представлением изменения различных слагаемых уравнения Бернулли по длине трубопровода. Диаграмма характеризует удельную механическую энергию потока и включает в себя три линии: линию полного напора, пьезометрическую линию и линию геометрического напора.

Линия полного напора характеризует полную удельную механическую энергию, то есть сумму кинетической и потенциальной энергий:

,при этом удельная потенциальная энергия давления при построении диаграммы определяется не абсолютным давлением, а избыточным.

Пьезометрическая линия характеризует удельную потенциальную энергию потока и представляет сумму двух слагаемых

.

Геометрическая линия, или линия геометрического напора характеризует уклон трубопровода, т. е. изменение координаты zоси трубопровода.

На рис.47 приведена диаграмма Бернулли для трубы переменного сечения. В первом сечении (1-1) полная удельная механическая энергия характеризуется величиной О₁А₁. По мере движения жидкости в трубе ее энергия расходуется, вследствие чего линия полного напора А₁А₂ всегда понижается. Если бы жидкость была невязкой, то полная удельная механическая энергия потока не менялась бы (линия А₁В) из-за отсутствия потерь. Расстояние между линиями полного напораА₁А₂ и пьезометрической С₁С₂ равно и увеличивается по потоку, так как сечение трубы уменьшается, а это приводит к увеличению средней скорости и, следовательно, кинетической энергии. В сечении 2-2 полная удельная механическая энергия потока характеризуется величиной О₂А₂ и она меньше, чем полная энергия в сечении 1-1 на величину потерь h (А₂В).

Показанная на диаграмме Бернулли линия геометрических напоров D₁D₂ характеризует изменение удельной потенциальной энергии положения z, являясь, по существу осью трубопровода.

Понятие гидравлического и пьезометрического уклона. В гидравлике различают гидравлический I и пьезометрический I_Pуклоны.

(2.22)

где — длина участка, для которого определяем гидравлический уклон;

— потери напора на участке потока длиной .

Если напорная линия криволинейная, гидравлический уклон будет различен в любой точке кривой. Например, гидравлический уклон в точке 1 напорной линии

(2.23)

И если пьезометрическая линия является криволинейной, то пьезометрический уклон в точке 1

При равномерном движении жидкости гидравлический и пьезометрический уклоны равны между собой, так как при равномерном движении живое сечение и средняя скорость потока постоянны и, следовательно, , тогда

Следует отметить, что пьезометрический уклон может быть или положительным, или отрицательным. Гидравлический уклон всегда будет положительным, так как напорная линия всегда понижается по направлению движения потока, поэтому обратного уклона не может быть.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)

Источник

Формулировка закона Бернулли и его математическое выражение

Обновлено: 02 Июня 2021

Принцип Бернулли заложил основы знания о движении жидкости, которое впоследствии перешло в самостоятельную науку — гидродинамику.

Физическая сущность закона Бернулли

Швейцарский математик и физик Даниил Бернулли родился в 1716 году в Голландии. За свою научную карьеру он получил звания Почетного члена Берлинской, Петербургской и Парижской академии наук, являлся членом Лондонского королевского общества. Главным научным трудом ученого является работа «Гидродинамика, или изъяснение сил и движений жидкости», опубликованная в 1733 году. Именно в этой книге были описаны физические основы механики жидкости.

Закон, названный его именем, Бернулли сформулировал во время работы в России, изучая взаимосвязь давления жидкости с ее скоростью. В математическом выражении он определяется уравнением Бернулли. Давайте разберемся, в чем состоит сущность закона.

Для начала определим, что закон Бернулли рассматривает движение потока несжимаемой идеальной жидкости, на которую действуют только силы тяжести и силы упругости.

Идеальная жидкость — это жидкость, в которой полностью отсутствует внутреннее трение и теплопроводность, ввиду чего, она лишена касательных напряжений между соседними слоями.

Подобная идеализация применяется при рассмотрении течения в гидродинамике. В законе Бернулли рассматривается стационарное течение жидкости — это движение слоев жидкости относительно друг друга и относительно ее самой, при котором скорость потока в некой конкретной точке не меняется, сохраняя свое постоянное значение. Давление при стационарном течении идеальной жидкости одинаково во всех поперечных сечениях трубки тока.

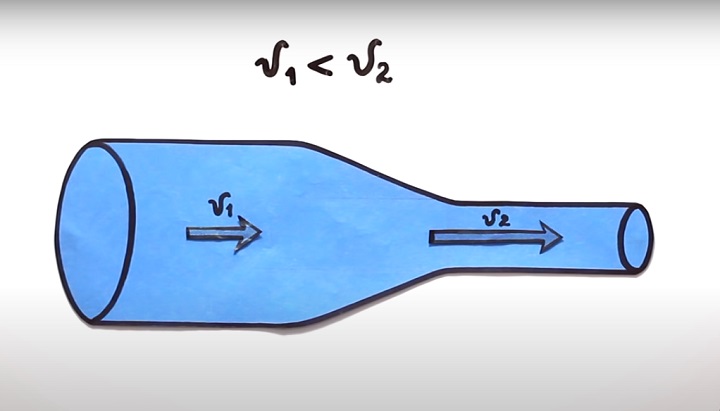
Для наглядности рассмотрим стационарное течение идеальной жидкости по трубе переменного сечения. В одном месте сечение этой трубки равно S1, а в другом — S2. При стационарном потоке через все сечения за определенный промежуток времени пройдет одинаковый объем жидкости, так как в ином случае, невозможность сжатия привела бы к ее разрыву. Таким образом, мы получаем уравнение неразрывности струи, определяющее соотношение между скоростью течения (v) и площадью сечения (S): S1v1=S2v2

При этом скорость давление в сечении S1 меньше, чем в сечении S2. Как вы думаете, в каком из сечений скорость течения жидкости будет больше? Казалось бы, что по логике, скорость должна увеличиваться в том месте, где больше давление. Однако, согласно закону Бернулли, скорость увеличивается с уменьшением площади сечения. В этом-то и состоит парадоксальность принципа.

Закон Бернулли гласит, в тех участках течения жидкости или газа, где скорость больше, давление меньше, и наоборот, с увеличением давления жидкости, протекающей в трубе, скорость ее движения уменьшается. То есть, где больше скорость (v), там меньше давление (p).

Чтобы убедиться в этом, достаточно провести небольшой опыт из подручных средств. Возьмите два шара одного размера и подвесьте их так, чтобы между ними сохранялось небольшое расстояние. Подуйте между шарами или пустите воздух из фена. Шары вместо того, чтобы отдалиться, притянутся друг к другу. Это прямое следствие описанного закона, так как в том месте, куда вы дули, давление стало уменьшаться, а скорость шаров возросла, приблизив их друг к другу.

Закон Бернулли как следствие закона сохранения энергии

Из уравнения неразрывности следует, что в идеальной жидкости сумма статистического и динамического давлений и скоростного напора постоянна в любом сечении вдоль трубы. Являясь следствием закона сохранения, вывод уравнение Бернулли для элементарной струйки жидкости выглядит так:

\rho\) — плотность жидкости, \(

v\) — скорость потока, \(

h\) — высота, на которой находится рассматриваемый элемент жидкости, \(

p\) — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, \(

g\) — ускорение свободного падения.

При этом давление P — это статическое давление, которое получается в результате взаимодействия соседних слоев жидкости. Величина ρv2/2 — это динамическое давление, обусловленное движением жидкости, а ρgh — это давление, образованное массой вертикального столба жидкости высотой h, создаваемое силой тяжести.

Все эти величины имеют специальные обозначения, где h — высота положения или геометрический напор, P / ρ∙g — пьезометрический напор, v2 / 2g — скоростной напор.

Сумма трех слагаемых уравнения называется полным напором (H), то есть для идеальной жидкости при стационарном течении сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.

Для трубы, расположенной горизонтально, где величина высоты остается неизменной, уравнение Бернулли упрощается и выглядит так:

Проявление закона Бернулли в жизни

Закон Бернулли описывает одно из основных свойств гидравлики. Эффект, описанный швейцарским ученым, широко проявляется в природе и быту. Также широко его применение в технике. На основе принципа Бернулли работают такие приборы, как пульверизатор, водоструйный насос, аэрограф.

Чтобы понять механизм устройства, рассмотрим строение пульверизатора, которое включает в себя вертикальную трубку и горизонтальное сопло. Вертикальную трубку опускают в жидкость, в то время как по соплу пропускают воздух. Атмосферное давление, которое больше давления в струе воздуха, заставляет жидкость подниматься по трубке. Следовательно, при попадании в струю воздуха, происходит распределение жидкости.

В повседневной жизни закон Бернулли можно наблюдать, сидя у камина. При сильном ветре скорость воздушного потока возрастает, и, соответственно, падает давление. И так как давление воздуха в комнате выше, пламя, уходит вверх по дымоходу.

Это свойство используется и в аэродинамике для объяснения того, как возникает подъемная сила самолета или другого летательного аппарата, которое тяжелее воздуха.

В истории имеются и случаи отрицательного проявления закона. В 1912 году произошло столкновение океанского парохода «Олимпик» с гораздо меньшим по масштабам крейсером «Гаук», который плыл параллельно пароходу на расстоянии около 100 метров. Вдруг «Гаук» резко двинулся прямо на «Олимпик» и протаранил его силой удара. Так как два корабля были друг к другу слишком близко, скорость воды между ними стала больше, чем с другой стороны, вызвав дополнительную силу. Следовательно, вместо того, чтобы отдалиться, корабли притянулись друг к другу, что и стало причиной катастрофы.

В природе закон Бернулли проявляется во время урагана, когда из-за сильного ветра с домов слетают крыши. Это происходит, потому что скорость, с которой движется воздух вверху, очень большая, тогда как на чердаке она равна нулю. Как вы уже узнаете, там, где скорость потока больше, давление меньше, а там, где скорость меньше, давление больше. В результате образовавшейся разности давлений ураган и срывает кровлю.

Существует еще большое количество интересных примеров, изучение которых во многом упрощает усвоение закона Бернулли. Если вам нужно определить проявление закона в каком-то конкретном явление, обращайтесь к специалистам сервиса Феникс.Хелп, которые помогут решить задачу любой сложности.

Источник