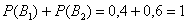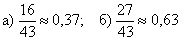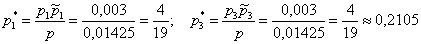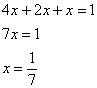завод делает детали шанс того что деталь будет плохой
Завод делает детали шанс того что деталь будет плохой
Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.
Откуда взяли цифру 0,94?Но ведь в задаче не написана эта цифра.
Батарейка либо бракованная, либо исправная. Вероятность того, что она бракованная по условию 0,06. Во всех остальных случаях она исправна. Вероятность того, что батарейка исправна равна 1-0,06=0,94
Можете ли объяснить, почему если умножить 0,06 на 0,06 — вероятность того, что обе батарейки бракованные, а после отнимаю её от единицы не получается тоже самое? Спасибо.
Умножая вероятности того, что батарейки неисправны, вы находите вероятность купить две неисправные батарейки. Вычитая из единицы найденную величину, вы получите вероятность противоположного события — покупки не двух неисправных батареек одновременно, а любой другой возможности: покупки двух исправных батареек или покупку одной исправной и одной неисправной батарейки.
Формулировка задания неверная. В первом предложении задачи говорится о бракованных батарейках. Во втором предложении говорят, что ТАКИХ батареек взято 2 штуки. Каких это таких? Должно быть объяснено слово ТАКИХ.
Таких — это таких батареек, которые могут быть бракованными с вероятностью 0,06. (А не других батареек, выпущенных на другом заводе и неисправных с вероятностью 0,1, например.)
1.8. Формулы Байеса
Материал тесно связан с содержанием предыдущего параграфа. Пусть событие 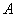
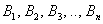
При условии, что событие 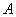
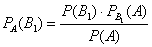
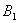
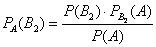
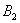
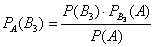
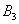
…
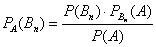
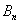
На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности гипотез, если они и так известны? Но на самом деле разница есть:
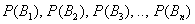
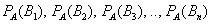
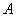
Рассмотрим это различие на конкретном примере:
Задача 60
На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии составляет 20%, а во второй – 10%. Наудачу взятое со склада изделие оказалось стандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии.
Первая часть решения состоит в использовании формулы полной вероятности. Иными словами, вычисления проводятся в предположении, что испытание ещё не произведено и событие «изделие оказалось стандартным» пока не наступило.
Рассмотрим две гипотезы:
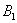
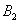
Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению: 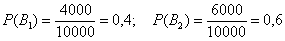
Контроль:
Рассмотрим зависимое событие: 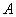
В первой партии 100% – 20% = 80% стандартных изделий, поэтому: 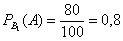
Аналогично, во второй партии 100% – 10% = 90% стандартных изделий и 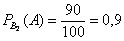
По формуле полной вероятности:
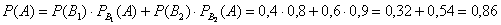
Часть вторая. Пусть наудачу взятое со склада изделие оказалось стандартным. Эта фраза прямо прописана в условии, и она констатирует тот факт, что событие 
а) 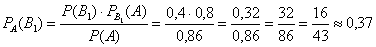
б) 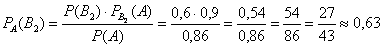
После переоценки гипотезы 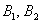
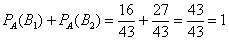
Ответ:
Понять смысл переоценки гипотез нам поможет Иван Васильевич, которой снова сменил профессию и стал директором завода. Он знает, что сегодня 1-й цех отгрузил на склад 4000, а 2-й цех – 6000 изделий, и приходит удостовериться в этом. Предположим, вся продукция однотипна и находится в одном контейнере. Естественно, Иван Васильевич подсчитал, что изделие, которое он сейчас извлечёт для проверки, с вероятностью 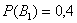
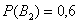
Но после того как выбранное изделие оказывается стандартным, он восклицает: «Какой же классный болт! – его скорее выпустил 2-й цех». Таким образом, вероятность второй гипотезы переоценивается в лучшую сторону 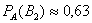
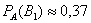
Вы скажете, чистый субъективизм? Отчасти – да, более того, сам Байес интерпретировал апостериорные вероятности как уровень доверия.
И, несмотря на то, что у байесовского подхода немало критиков, в нём есть и объективное зерно. Ведь вероятности того, что изделие будет стандартным (0,8 и 0,9 для 1-го и 2-го цехов соответственно) это предварительные (априорные) и средние оценки.
Но, выражаясь философски – всё течёт, всё меняется, и вероятности в том числе. Вполне возможно, что на момент исследования более успешный 2-й цех повысил процент выпуска стандартных изделий (и / или 1-й цех снизил), и если проверить бОльшее количество либо все 10 тысяч изделий на складе, то переоцененные значения 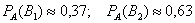
Кстати, если Иван Васильевич извлечёт нестандартную деталь, то наоборот – он будет больше «подозревать» первый цех и меньше – второй. Предлагаю убедиться в этом самостоятельно:
Задача 61
На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии 20%, во второй – 10%. Наудачу взятое со склада изделие оказалось нестандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии.
Условие отличатся двумя буквами, которые я выделил жирным шрифтом. Задачу можно решить с «чистого листа», или воспользоваться результатами предыдущих вычислений. В образце я провёл полное решение, но чтобы не возникло формальной накладки с предыдущей задачей, событие «наудачу взятое со склада изделие будет нестандартным» обозначено через 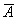
Байесовская схема переоценки вероятностей встречается повсеместно, причём её активно эксплуатируют и различного рода мошенники. Рассмотрим ставшее нарицательным АО на три буквы, которое привлекает вклады населения, якобы куда-то их инвестирует, исправно выплачивает 2% в день и т.д. Что происходит? Проходит день за днём, месяц за месяцем и всё новые и новые факты, донесённые путём рекламы и «сарафанным радио», только повышают уровень доверия к финансовой пирамиде (апостериорная байесовская переоценка в связи с произошедшими событиями!). То есть, в глазах вкладчиков происходит постоянное увеличение вероятности того, что «это серьёзная контора»; при этом вероятность противоположной гипотезы («это очередной лохотрон»), само собой, уменьшается и уменьшается. Дальнейшее, думаю, понятно. Примечательно, что заработанная репутация даёт организаторам время успешно скрыться от Ивана Васильевича, который остался не только без партии болтов, но и без штанов.
К не менее любопытным примерам мы вернёмся чуть позже, а пока на очереди, пожалуй, самый распространенный случай с тремя гипотезами:
Задача 62
Электролампы изготавливаются на трех заводах. 1-ый завод производит 30% общего количества ламп, 2-й – 55%, а 3-й – остальную часть. Продукция 1-го завода содержит 1% бракованных ламп, 2-го – 1,5%, 3-го – 2%. В магазин поступает продукция всех трех заводов. Купленная лампа оказалась с браком. Какова вероятность того, что она произведена 2-м заводом?
Заметьте, что в задачах на формулы Байеса в условии обязательно фигурирует некое произошедшее событие, в данном случае – покупка лампы.
Событий прибавилось, и решение удобнее оформить в «быстром» стиле.
Алгоритм точно такой же: на первом шаге находим вероятность того, что купленная лампа вообще окажется бракованной.
Пользуясь исходными данными, переводим проценты в вероятности:
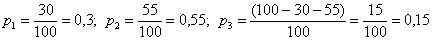
Контроль: 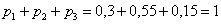
Аналогично:
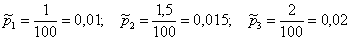
По формуле полной вероятности: 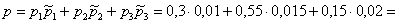
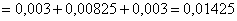
Шаг второй. Пусть купленная лампа оказалась бракованной (событие произошло)
По формуле Байеса:
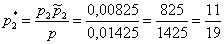
Ответ: 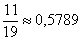
Почему изначальная вероятность 2-й гипотезы 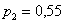
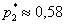
Интересно заметить, что вероятности 1-й и 3-й гипотез, переоценились в ожидаемых направлениях и сравнялись:
Контроль: 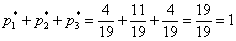
К слову, о заниженных и завышенных оценках:
Задача 63
В студенческой группе 3 человека имеют высокий уровень подготовки, 19 человек – средний и 3 – низкий. Вероятности успешной сдачи экзамена для данных студентов соответственно равны: 0,95; 0,7 и 0,4. Известно, что некоторый студент сдал экзамен. Какова вероятность того, что:
а) он был подготовлен очень хорошо;
б) был подготовлен средне;
в) был подготовлен плохо.
Проведите вычисления и проанализируйте результаты переоценки гипотез.
Предложенная задача приближена к реальности и особенно правдоподобна для группы студентов-заочников, где преподаватель практически не знает способностей того или иного студента. При этом результат может послужить причиной довольно-таки неожиданных последствий (особенно это касается экзаменов в 1-м семестре). Если плохо подготовленному студенту посчастливилось с билетом, то преподаватель с большой вероятностью сочтёт его хорошо успевающим или даже сильным студентом, что принесёт неплохие дивиденды в будущем (естественно, нужно «поднимать планку» и поддерживать свой имидж). Если же студент 7 дней и 7 ночей учил, «зубрил», повторял, но ему просто не повезло, то дальнейшие события могут развиваться в самом скверном ключе – с многочисленными пересдачами и балансировкой на грани «вылета».
Что и говорить, репутация – это важнейший капитал, не случайно многие корпорации носят имена-фамилии своих отцов-основателей, которые руководили делом 100-200 лет назад и прославились своей безупречной репутацией.
Да, байесовский подход в известной степени субъективен, но… так устроена жизнь!
Закрепим материал заключительным индустриальным примером, в котором я расскажу ещё об одном техническом приёме решения:
Задача 64
Три цеха завода производят однотипные детали, которые поступают на сборку в общий контейнер. Известно, что первый цех производит в 2 раза деталей, чем второй цех, и в 4 раза больше третьего цеха. В первом цехе брак составляет 12%, во втором – 8%, в третьем – 4%. Для контроля из контейнера берется одна деталь. Какова вероятность того, что она окажется бракованной? Какова вероятность того, что извлечённую бракованную деталь выпустил 3-й цех?
…таки Иван Васильевич снова на коне, должен же быть у фильма счастливый конец 🙂
Решение: в отличие от предыдущих задач здесь в явном виде задан вопрос, который разрешается с помощью формулы полной вероятности. Но с другой стороны, условие немного «зашифровано», и разгадать этот ребус нам поможет школьный навык составлять простейшие уравнения. За «икс» удобно принять наименьшее значение:
Пусть 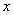
По условию, первый цех производит в 4 раза больше третьего цеха, поэтому доля 1-го цеха составляет 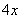
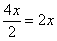
Составим и решим уравнение:
Таким образом: 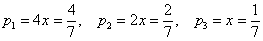
Контроль: 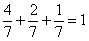
За «икс» изначально можно было принять долю 1-го либо долю 2-го цеха – вероятности выйдёт такими же. Но, так или иначе, самый трудный участок пройден, и решение входит в накатанную колею:
Из условия находим:
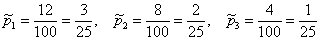
По формуле полной вероятности: 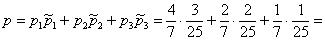
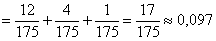
Вопрос второй: какова вероятность 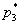
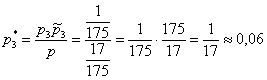
Коль скоро в условии нет пунктов «а» и «бэ», то ответ лучше снабдить текстовыми комментариями:
Ответ: 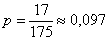
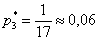
Как видите, задачи на формулу полной вероятности и формулы Байеса достаточно простЫ, и, наверное, по этой причине в них так часто пытаются затруднить условие, о чём я уже упоминал в начале параграфа.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин