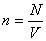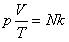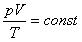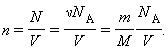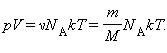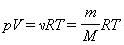что означает идеальный газ

Идеальный газ

Полезное

Смотреть что такое «Идеальный газ» в других словарях:

ИДЕАЛЬНЫЙ ГАЗ — теор. модель газа, в к рой не учитывается вз ствие ч ц газа (ср. кинетич. энергия ч ц много больше энергий их вз ствия). Различают классич. и квант. И. г. Св ва классического И. г. описываются законами классич. физики Клапейрона уравнением и его… … Физическая энциклопедия

идеальный газ — Невязкий нетеплопроводный газ, при движении которого возникают только нормальные напряжения. Примечание В идеальном газе вектор силы, действующей на любую выбранную в нем площадку, ортогонален к этой площадке. [ГОСТ 23281 78] Тематики… … Справочник технического переводчика

ИДЕАЛЬНЫЙ ГАЗ — идеализированная модель газа; в идеальном газе силы взаимодействия между частицами (атомами, молекулами) пренебрежимо малы. К идеальному газу близки разреженные реальные газы при температурах, далеких от температуры их конденсации. Зависимость… … Большой Энциклопедический словарь

Идеальный газ — Термодинамика Статья является частью одноименной сер … Википедия

идеальный газ — идеализированная модель газа; в идеальном газе силы взаимодействия между частицами (атомами, молекулами) пренебрежимо малы. К идеальному газу близки разреженные реальные газы при температурах, далёких от температуры их конденсации. Зависимость… … Энциклопедический словарь

идеальный газ — idealiosios dujos statusas T sritis fizika atitikmenys: angl. ideal gas; perfect gas vok. ideales Gas, n; vollkommenes Gas, n rus. идеальный газ, m; совершенный газ, m pranc. gaz idéal, m; gaz parfait, m … Fizikos terminų žodynas

Идеальный газ — понятие физики, в узком смысле, теоретическая модель газа, в которой пренебрегают размерами и взаимодействиями частиц газа и учитывают лишь их упругие столкновения. В широкой трактовке, идеальный газ состоит из частиц, представляющих собой… … Концепции современного естествознания. Словарь основных терминов

идеальный газ — idealiosios dujos statusas T sritis Standartizacija ir metrologija apibrėžtis Dujos, kurių dalelės nesąveikauja tarpusavyje. atitikmenys: angl. ideal gas; perfect gas vok. ideales Gas, n rus. идеальный газ, m pranc. gaz parfait, m … Penkiakalbis aiškinamasis metrologijos terminų žodynas

идеальный газ — idealiosios dujos statusas T sritis chemija apibrėžtis Dujos, kurių molekulės tarpusavyje nesąveikauja. atitikmenys: angl. ideal gas; perfect gas rus. идеальный газ … Chemijos terminų aiškinamasis žodynas

идеальный газ — idealiosios dujos statusas T sritis Energetika apibrėžtis Dujos, kurių dalelės nesąveikauja. Joms galioja idealiųjų dujų lygtis (Klapeirono lygtis). atitikmenys: angl. ideal gas vok. ideales Gas, n rus. идеальный газ, m pranc. gaz idéal, m … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

Идеальный газ — газ, в котором взаимодействием молекул можно пренебречь, а обмен энергией совершается только при упругих столкновениях молекул. К идеальному газу близки разреженные газы, вдали от температуры их конденсации … Начала современного естествознания

Источник

Как сказал.

Все знают, что это невозможно. Но вот приходит невежда, которому это неизвестно — он-то и делает открытие.

Альберт Эйнштейн

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Урок 15. Лекция 15. Идеальный газ

Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.

Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:

Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.

Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.

Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.

Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.

Модель идеального газа. Связь между давлением и средней кинетической энергией.

Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.

Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)

Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.

Свойства идеального газа:

Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.

Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.

До настоящего времени употребляются внесистемные единицы давления:

техническая атмосфера 1 ат = 9,81-104 Па;

физическая атмосфера 1 атм = 1,013-105 Па;

миллиметры ртутного столба 1 мм рт. ст.= 133 Па;

1 атм = = 760 мм рт. ст. = 1013 гПа.

Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени дей­ствует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.

Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.

Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.

В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υ_x скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υ_y скорости, параллельная стенке, остается неизменной.

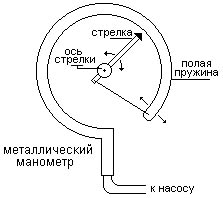
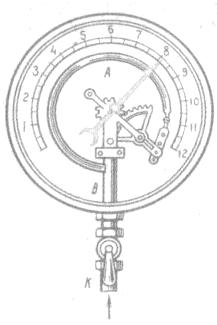
Приборы, измеряющие давление, называют манометрами. Манометры фиксиру­ют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.

Металлический манометр – для измерения больших давлений.

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.

Основное уравнение молекулярно-кинетической теории идеального газа.

Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул

n = N/V – число молекул в единице объема, или концентрация молекул;

Так как средняя кинетическая энергия поступательного движения молекул E = m₀*v 2 /2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m₀· v 2 )/2 = 2/3·E·n

Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.

Так как m₀·n = m₀·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v 2

Объединенный газовый закон.

Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.

Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.

Всякое изменение состояния газа называется термодинамическим процессом.

В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.

Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.

Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.

Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

где n – концентрация молекул, N – общее число молекул, V – объем газа

Тогда получим 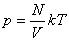или

Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит

При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.

Уравнение Клайперона можно записать в другой форме.

Здесь N – число молекул в сосуде, ν – количество вещества, N_А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.

Ее численное значение в СИ R = 8,31 Дж/моль·К

называется уравнением состояния идеального газа.

В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`

Для одного моля любого газа это соотношение принимает вид: pV=RT

Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.

Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)

ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:

pS = F – сила давления.

Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.

Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.

Источник

Идеальный газ

Содержание:

Идеальный газ – это модель разреженного газа, в которой пренебрегается взаимодействием между молекулами. Силы взаимодействия между молекулами довольно сложны.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Идеальный газ

Идеальный газ – это наиболее простая модель системы, состоящей из большого количества частиц. Это газ, который состоит из материальных точек, имеющих конечную массу, но не имеющих объема.

При изучении явлений в природе и технике практически невозможно учесть все факторы, влияющие на ход того или иного явления. Однако из опыта всегда можно установить важнейшие из них. Тогда всеми другими факторами, не имеющими решающего влияния на ход явления, можно пренебречь. На этой основе создается идеализированное (упрощенное) представление о таком явлении. Затем теоретически изучают ход явления в идеальных условиях, т. е. при действии только важнейших факторов. Созданная на этой основе модель явления помогает изучать реально происходящие процессы и предвидеть их ход в различных случаях. Рассмотрим одно из таких идеализированных понятий.

Выше говорилось (§ 3.1), что физические свойства газа определяются хаотическим движением его молекул, а взаимодействие молекул газа существенного влияния на его свойства не оказывает, причем это взаимодействие имеет характер столкновений, а притяжением молекул часто можно пренебречь. Силы отталкивания возникают при столкновении молекул на очень короткое время, и большую часть времени молекулы газа движутся как свободные частицы.

Это позволяет ввести понятие идеального газа, в котором силы притяжения между молекулами полностью отсутствуют и часто можно вообще не учитывать взаимодействия между молекулами, считая их совершенно свободными. Если такая модель газа приемлема, то свойства реальных газов не должны заметно зависеть от их природы. При невысоких давлениях и не очень низких температурах это действительно так.

Вспомним, что собственный объем молекул газа составляет ничтожную часть от объема, занятого газом (если газ не сильно сжат); это, кстати сказать, тоже соответствует тому, что природа молекул газа не влияет существенно на его свойства. Следовательно, молекулы идеального газа всегда должны иметь пренебрежимо малый объем по сравнению с общим объемом, занятым газом. В этом смысле молекулы одноатомного идеального газа можно представить в виде материальных точек, а молекулы многоатомного газа — в виде жестко связанных материальных точек.

Итак, под идеальным газом подразумевают такой газ, в котором можно пренебречь взаимодействием между молекулами, а молекулы принять за материальные точки. Поскольку молекулы идеального газа ни при каких условиях не притягиваются друг к другу, он должен оставаться в газообразном состоянии при любых внешних условиях.

Понятие идеального газа полезно в том отношении, что ‘все реальные газы при небольших давлениях и не очень низких температурах подчиняются простым общим законам, в точности справедливым лишь для идеального газа. Изучение свойств идеального газа позволило сделать ряд теоретических выводов, углубляющих наши представления о явлениях природы.

При высоких давлениях молекулы реального газа сближаются настолько, что силы притяжения начинают играть заметную роль. Существенное влияние на поведение молекул в этих условиях оказывает и собственный объем молекул. Поэтому при высоких давлениях свойства реальных газов зависят от природы газа и существенно отличаются от свойств идеального газа. Это же относится и к реальным газам при низких температурах. По своим свойствам ближе всего к идеальному газу подходят водород и гелий при не слишком больших давлениях и не очень низких температурах.

Основное уравнение молекулярно-кинетической теории газов

Вспомним, что давление газа на стенку сосуда обусловлено ударами молекул; Чем больше кинетическая энергия поступательного движения каждой молекулы, тем больше сила, возникающая при ее ударе о стенку. Кроме того, чем больше молекул в единице объема п₀, тем чаще они ударяются о стенку. Поэтому давление газа прямо пропорционально средней кинетической энергии поступательного движения молекул газа и их числу в единице объема:

Эту формулу можно вывести на основе молекулярно-кинетической теории. Формула (4.1) имеет очень большое значение и называется основным уравнением молекулярно-кинетической теории газов.

Покажем, как получается формула (4.1).

Возьмем сосуд в форме куба с ребром l. Допустим, что внутри куба в каждой единице объема Содержится одинаковых молекул газа. Так как молекулы движутся, то каждая из них обладает количеством движения (импульсом) (здесь т — масса одной молекулы, — скорость ее движения). Будем считать удары молекул о стенку абсолютно упругими. Тогда, если молекула движется перпендикулярно к стенке сосуда (рис. 4.1), при ударе она сначала останавливается, т. е. теряет импульс , а затем отскакивает от стенки и движется в противоположную сторону со скоростью — , т. е. приобретает противоположно направленный импульс —. Таким образом, изменение импульса молекулы в процессе удара равно , а стенка получает такой же по модулю импульс .

Пусть эта молекула беспрепятственно движется между левой и правой стенками куба. При каждом ударе она сообщает стенке импульс . В соответствии с вакоинами механики средняя сила воздействия молекулы на стенку , где — время движения молекулы от одной стенки до другой и обратно, т. е. , поскольку молекула наносит стенке удары с таким промежутком времени. Следовательно,

Сила давления газа на стенку сосуда равна сумме сил ударов отдельных молекул об эту стенку:

где N — общее число молекул, летающих между двумя противоположными стенками куба, а — средняя квадратичная скорость молекул (§ 2.4).

Поскольку число молекул в единице объема равно , суммарное число молекул в кубе равно . Из-за полной хаотичности движения молекул для каждой из них все направления движения равновероятны. Поэтому можно считать, что вдоль каждого из трех взаимно перпендикулярных направлений движется в среднем 1/3 общего числа молекул. Итак, при подсчете давления можно принять, что между двумя противоположными стенками куба по перпендикуляру к ним движется 1/3 общего числа молекул, т. е. . Таким образом,

Поскольку получаем . Так как

то окончательно имеем .

Зависимость давления газа от температуры при постоянном объеме

Рассмотрим, как зависит давление газа от температуры, когда его масса и объем остаются постоянными.

Возьмем закрытый сосуд с газом и будем нагревать его (рис. 4.2).

Температуру газа t будем определять с помощью термометра, а давление — манометром М. Сначала поместим сосуд в тающий снег и давление газа при 0°С обозначим , а затем будем постепенно нагревать наружный сосуд и записывать значения и для газа. Оказывается, что график зависимости от построенный на основании такого опыта, имеет вид прямой линии (рис. 4.3, а). Если продолжить этот график влево, то он пересечется с осью абсцисс в точке А, соответствующей нулевому давлению газа.

Из подобия треугольников на рис. 4.3, а можно записать:

Если обозначить постоянную через , то получим

По смыслу коэффициент пропорциональности в описанных опытах должен выражать зависимость изменения давления газа от его рода.

Величина , характеризующая зависимость изменения давления газа от его рода в процессе изменения температуры при постоянном объеме и неизменной массе газа, называется температурным коэффициентом давления. Температурный коэффициент давления показывает, на какую часть давления газа, взятого при (УС, изменяется его давление при нагревании на 1°С (4.2).

Выведем единицу температурного коэффициента в СИ:

Выясним, как можно определить давление любого газа при произвольной температуре t. Из рис. 4.3, а видно, что

Подставив эти значения и в формулу (4.2а), получим

Поскольку , то при решении задач формулу (4.3) можно использовать в следующем виде:

Абсолютный нуль

В предыдущем параграфе было отмечено, что точка А на рис. 4.3 соответствует р=0. Выясним, при каких условиях давление идеального газа должно равняться нулю. Поскольку давление газа определяется ударами хаотически движущихся молекул, то уменьшение давления при охлаждении газа объясняется уменьшением средней энергии поступательного движения молекул газа ; давление газа будет равно нулю, когда станет равна нулю энергия поступательного движения его молекул. Это видно также из формулы (4.1):

(в опытах, описанных в § 4.3, остается постоянным и не равным нулю).

Теперь видно, что для охлаждения газа должен быть предел, который соответствует отсутствию поступательного движения у молекул: температуру, при которой должно прекратиться поступательное движение молекул, называют абсолютным нулем.

Выясним теперь, при какой именно температуре должны остановиться молекулы идеального газа. Так как идеальный газ остается в газообразном состоянии при всех температурах, формула (4.4) справедлива и для абсолютного нуля. Поэтому

Поскольку , имеем

Напомним, что это же значение для получается из рис. 4.3, б. Более точное значение температуры абсолютного нуля —273,15°С. Выдающийся английский ученый В. Кельвин выдвинул идею о том, что полученное значение абсолютного нуля соответствует прекращению поступательного движения молекул всех веществ. Отметим, что температуры ниже абсолютного нуля в природе быть не может. Действительно, при температуре абсолютного нуля уже нельзя было бы отнимать энергию теплового движения у молекул тела и понижать далее температуру тела (энергия теплового движения не может быть отрицательной). Из теоретических соображений следует, что невозможно охладить какое-либо тело даже до температуры абсолютного нуля. Однако достичь температуры, очень близкой к абсолютному нулю, можно. В физических лабораториях получена температура, отличающаяся от абсолютного нуля всего на тысячные доли градуса.

Заметим, что при приближении к абсолютному нулю прекращается только тепловое движение молекул, а не всякое движение вообще: внутри молекул элементарные частицы продолжают движение.

Термодинамическая шкала температур

Абсолютная температура. Вспомним, что на практике за 0° условно принимается температура таяния льда при нормальном давлении, а за 100° — температура кипения воды при нормальном давлении. Одна сотая этого интервала температур является практической единицей температуры — градусом Цельсия (°С). Однако при делении интервала между 0°С и 100°С на сто равных частей у ртутных и спиртовых термометров их показания совпадают только при 0°С и при 100°С. Следовательно, расширение этих веществ при нагревании происходит неравномерно и получить единую температурную шкалу таким способом нельзя.

Чтобы создать единую температурную шкалу, нужно иметь величину, изменение которой при нагревании или охлаждении не зависело бы от рода термометрического вещества. Такой величиной может служить давление газа, так как температурный коэффициент давления для не слишком плотных газов не зависит от природы газа и имеет такое же значение, как и для идеального газа. Наилучшим термометрическим телом был бы идеальный газ. Поскольку свойства разреженного водорода ближе всего подходят к свойствам идеального газа, то целесообразнее всего измерять температуру по водородному термометру, который представляет собой закрытый сосуд с разреженным водородом, соединенный с чувствительным манометром. Так как давление и температура водорода связаны соотношением (4.3), то по показанию манометра можно определять температуру.

Шкалу температур, установленную по водородному термометру, у которой 0° соответствует температуре таяния льда, а 100° — температуре кипения воды, называют шкалой Цельсия.

Отметим, что нуль на шкале Цельсия определен условно. Размер градуса тоже определен произвольно. Это означает, что с научной точки зрения допустимо иное построение температурной шкалы.

Целесообразный выбор шкалы температур позволяет упростить формулы и глубже понять физический смысл наблюдаемых закономерностей. С этой целью по предложению Кельвина была введена новая температурная шкала, которая теперь называется термодинамичеекой шкалой температур. Иногда ее называют шкалой Кельвина. По этой шкале за начало отсчета принимается температура абсолютного нуля, а размер градуса определяют так, чтобы он по возможности точно совпадал с градусом Цельсия.

В СИ единица температуры является основной и называется Кельвином (К), а для отсчета температуры принимается термодинамическая шкала температур.

По международному соглашению размер кельвина определяется из следующего условия: температура тройной точки воды (§ 12.8) считается точно равной 273,16 К. Следовательно, если температурный интервал между абсолютным нулем н температурой тройной точки воды по шкале водородного термометра разделить на 273,16 части, то одна такая часть н определяет размер кельвина. Так как тройной точке воды соответствует температура 0,01°С, то температура таяния льда по новой шкале будет 273,15 К. Поскольку кельвин по величине равен градусу Цельсия, то температура-кипения воды при нормальном давлении будет 373,15 К. Для упрощения в дальнейшем температуры таяния льда н кипения воды соответственно будут считаться равными 273 и 373 К.

Температура, выраженная в Кельвинах по термодинамической шкале, называется абсолютной и обозначается Т. Связь между абсолютной температурой и температурой по стоградусной шкале выражается следующим образом:

Обычно пользуются приближенной формулой

На рис. 4.4 эта связь показана схематически. Из этой схемы видно, что абсолютная температура не может быть отрицательной.

Связь между температурой и кинетической энергией молекул газа. Постоянная Больцмана

Найденная Шарлем зависимость от изображена на рис. 4.3, а. Если перенести начало координат в точку А, то график будет проходить через начало координат. Все значения температуры увеличатся на 273°С, поскольку длина отрезка ОА равна 273°С (§ 4.3). Это соответствует формуле (4.6): Т=273+, т. е. по оси абсцисс теперь откладываются значения абсолютной температуры (рис. 4.5). В этом случае между и Т получается прямо пропорциональная зависимость. Действительно, из подобия треугольников на рис. 4.5 имеем

Итак, с одной стороны, давление газа прямо пропорционально его абсолютной температуре, а с другой стороны (см. (4.1)), прямо пропорционально средней кинетической энергии поступательного движения молекул газа (при постоянной массе и неизменном объеме). Это означает, что величина прямо пропорциональна абсолютной температуре газа Т. По предложению выдающегося немецкого ученого Л. Больцмана коэффициент пропорциональности в зависимости от Т. записывают в виде (3/2) :

Тогда, после подстановки этого значения в формулу (4.1) , получим простое выражение

Из (4.9) видно, что давление газа не зависит от его природы, а определяется только концентрацией молекул и температурой газа Т.

Постоянную величину в (4.8) и (4.9) принято называть постоянной Больцмана. В СИ она имеет следующее значение (§ 5.3):

Из формулы (4.8) следует, что среднее значение кинетической энергии поступательного движения молекул не зависит от природы газа, а определяется только его температурой.

Поскольку при заданной температуре Т средние значения энергии поступательного движения молекул для различных газов одинаковы, можно записать , откуда получаем

При одинаковой температуре средние квадратичные скорости движения молекул обратно пропорциональны корням квадратным из масс молекул.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник