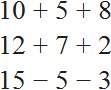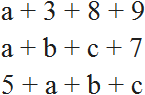что означает математическое выражение
Выражение (математика)
В математике, (математическое) выражение — конечная комбинация символов, которая правильно построена согласно правилам, зависящим от контекста.
Математические символы могут обозначать числа (константы), переменные, операции, функции, пунктуацию, группирование и другие аспекты логического синтаксиса.
Содержание
[править] Примеры
Синтаксис выражений варьируется от простого:
до сложного составного:
[править] Формы
Математические выражения включают арифметические, полиномиальные, алгебраические выражения, замкнутые формы, аналитические выражения. Таблица ниже показывает некоторые сходства и различия между ними.
| Арифметические выражения | Полиномиальные выражения | Алгебраические выражения | Замкнутые формы | Аналитические выражения | |
|---|---|---|---|---|---|
| Константа | Да | Да | Да | Да | Да |
| Переменная | Да | Да | Да | Да | Да |
| Арифметическая операция | Да | Да | Да | Да | Да |
| Факториал | Да | Да | Да | Да | Да |
| Целая экспонента | Нет | Да | Да | Да | Да |
| Корень N-ой степени | Нет | Нет | Да | Да | Да |
| Рациональная экспонента | Нет | Нет | Да | Да | Да |
| Иррациональная экспонента | Нет | Нет | Нет | Да | Да |
| Логарифм | Нет | Нет | Нет | Да | Да |
| Тригонометрич. функция | Нет | Нет | Нет | Да | Да |
| Обратная тригонометрич. функция | Нет | Нет | Нет | Да | Да |
| Гиперболическая функция | Нет | Нет | Нет | Да | Да |
| Обратная гиперболическая функция | Нет | Нет | Нет | Да | Да |
| Гамма функция | Нет | Нет | Нет | Нет | Да |
| Функция Бесселя | Нет | Нет | Нет | Нет | Да |
| Специальная функция | Нет | Нет | Нет | Нет | Да |
| Непрерывная функция | Нет | Нет | Нет | Нет | Да |
| Бесконечная последовательность | Нет | Нет | Нет | Нет | Да |
| Формальная степенная последовательность | Нет | Нет | Нет | Нет | Нет |
| Дифференциал | Нет | Нет | Нет | Нет | Нет |
| Предел | Нет | Нет | Нет | Нет | Нет |
| Интеграл | Нет | Нет | Нет | Нет | Нет |
[править] Синтаксис и семантика
[править] Синтаксис
Быть выражением является синтаксическим понятием.
Выражение должно быть правильно построенным: операторы должны иметь нужное количество входов в подходящих позициях, символы, подаваемые на эти входы, должны быть значимыми, и т. д. Цепочки символов, нарушающие правила синтаксиса, построены некорректно и не образуют приемлемого математического выражения.
Например, в обычной арифметической нотации выражение 2 + 3 построено правильно, но следующее выражение непригодно:
[править] Семантика
Семантика изучает значения. Формальная семантика занимается приложением значений к выражениям.
В алгебре выражение может использоваться для обозначения величины,, которая зависит от величин переменных, входящих в выражении. Определение этой величины зависит от семантики, присвоенной символам выражения. Эти семантические правила могут объявить, что некоторые выражения не определяют никакой величины (например, когда они включают деление на 0). Говорят, что такие выражения имеют неопределенное значение, но тем не менее. они — правильно построенные выражения. Вообще говоря, значение выражений не сводится только к обозначению величин; например, выражение может обозначать условие, или уравнение, которое должно быть решено, или может трактоваться как некоторый объект в своем собственном контексте, который управляется согласно определенным правилам. Определенные выражения, которые обозначают величину, одновременно фиксируют необходимое условие, которое считается принятым.
[править] Формальные языки и лямбда-исчисление
Формальные языки позволяют уточнить (формализовать) понятие правильно построенных выражений.
В 1930-х годах новый вид выражений, названных лямбда-выражениями, был введен А. Черчом и С. Клини для определения функций и их вычислений. Эти выражения формируют основание формальной системы лямбда-исчисление, используемой в математической логике и теории языков программирования.
Эквивалентность двух лямбда-выражений неразрешима. Неразрешимость также имеет место для выражений, представляющих действительные числа, построенные из целых чисел с использованием арифметических операций, логарифмов и экспоненциалов (теорема Ричардсона).
[править] Переменные
Многие математические выражения содержат переменные. Некоторая переменная может рассматриваться как свободная или связанная. Для данной комбинации величин свободных переменных выражение может быть вычислено, однако для некоторых других комбинаций значение выражения может остаться неопределенным. Например, выражение
вычисляемое для x = 10, y = 5, дает 2; но оно не определено для y = 0.
Таким образом выражение представляет функцию, входы (аргументы) которой составляют величины, присвоенные свободным переменным, и чей результат — вычисленная величина выражения. Результат вычисление выражения зависит от определения математических операторов и от системы величин, которая является её контекстом.
Говорят, что два выражения эквивалентны, если для каждой комбинации величин свободных переменных, оба выражения дают тот же самый результат, то есть они представляют одну и ту же функцию. Например, выражение
имеет свободную переменную x, связанную переменную n, константы 1, 2, и 3, два вхождения неявного (имплицитного) оператора умножения, и оператор суммирования. Выражение эквивалентно более простому выражению 12x. Значение для x = 3 и n=3 равно 36.
Числовые, буквенные выражения и выражения с переменными: определения, примеры
В математике принято использовать свои обозначения. Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.
Числовые выражения
Конечно, числовые выражения содержат не только знаки «плюс» и «минус». Они могут включать деление и умножение, содержать скобки, степени, корни, логарифмы и состоять из нескольких действий.
Учитывая все сказанное, дадим определение. Что такое числовое выражение?
Определение. Числовое выражение
Числовым выражением считается только та комбинация, которая составлена с учетом математических правил.
Поясним данное определение.
Во-первых, числа. Математическое выражение может содержать любые числа. Это значит, что в математическом выражении можно встретить:
деление в выражениях может присутствовать как в виде знака, так и в виде дробной черты.
Скобки в числовых выражениях
Согласно определению, числовые выражения могут содержать степени, корни, логарифмы, тригонометрические и обратные тригонометрическим функции. Приведем пример такого числового выражения:
В качестве примера использования в числовых выражениях специальных знаков, можно привести знак модуля.
Буквенные выражения
После знакомства с числовыми выражениями можно вводить понятие буквенных выражений. Интуитивно понятно, что в них вместо чисел используются буквы. Но обо всем по порядку.
Запишем числовое выражение, но вместо одного числа оставим пустой квадратик.
Определение. Буквенное выражение
Выражение, в котором буквы заменяняют некоторые цифры, называется буквенным выражением. Буквенное выражение должно содержать по крайней мере одну букву.
Приведем пример сложного буквенного выражения.
Выражения с переменными
В рассмотренных выше буквенных выражениях буква обозначала какое-то конкретное числовое значение. Величина, которая может принимать ряд различных значений, называется переменной. Выражение с такой величиной, соответственно, называются выражением с переменной.
Определение. Выражения с переменными
Вообще буквенные выражения и выражения с переменными позволяют посмотреть на задачу вне контекста конкретных чисел, то есть более широко. Они широко используются в математическом анализе для формулировок и доказательств.
Внешний вид буквенного выражения не позволяет узнать, являются входящие в него буквы переменными, или нет. Для этого нужно знать условия конкретной задачи, описываемой выражением. Вне контекста ничто не мешает считать входящие в выражение буквы переменными. Таким образом, разница между понятиями «буквенное выражение» и «выражение с переменными» нивелируется.
Числовые выражения и буквенные выражения — правила
При решении примеров и уравнений нужно четко отличать — что такое числовые выражение, а что такое буквенные выражения. Поэтому сегодня пройдем эту тему и посмотрим видео. Итак, выучите правила.
Правила математики о числовых и буквенных выражениях
Число, которое получается в результате выполнения математических операций, входящих в это числовое выражение, называется значением числового выражения.
Числа, которые заменяют букву, называются значениями этой буквы.
Чтобы запомнить правила, давайте обратимся к примерам. Примеры — самый простой наглядный способ запомнить утверждения, приведенные выше.
Примеры числовых выражений
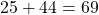
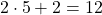
Посмотрите еще примеры числовых выражений:
Примеры буквенных выражений
Примеры буквенных выражений:
Буквенных выражений может быть множество. Для буквенных выражений каждая буква — это определенное число. Или множество разных чисел.
Когда применяются буквенные выражения
Буквенные выражения применяются тогда, когда нам надо, например, ввести формулу для нахождения той или иной величины. Например, вы знаете — что периметр прямоугольника, это сумма всех его сторон. Для периметра в общем виде можно записать буквенное выражение:
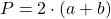

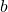
В правой части вы увидели буквенное выражение, значениями букв 
Математические выражения
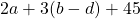
Число перед буквой в математическом выражении — это коэффициент, означающий, что это число умножается на букву, которая может иметь переменное значение.
Буквенные, числовые и математические выражения — необходимо различать, чтобы понимать условия задачи, например, вас могут попросить упростить математическое выражение или попросить найти значение числового выражения. Поэтому необходимо знать — что это такое.
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
Значение переменной a подставляется в исходное выражение.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
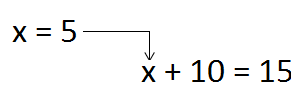
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b
Решение:
Значение выражения
Фраза « выполнить действие » означает выполнить одну из операций действия.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры: