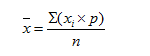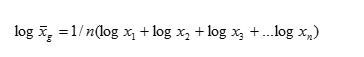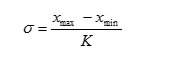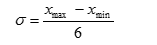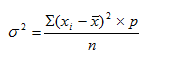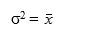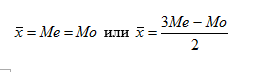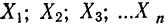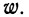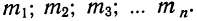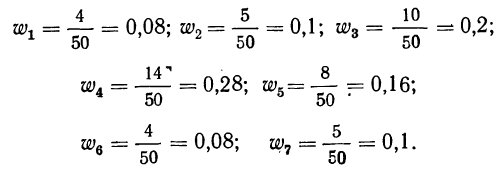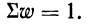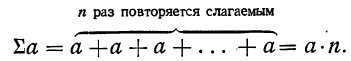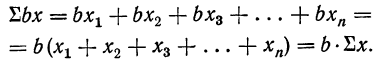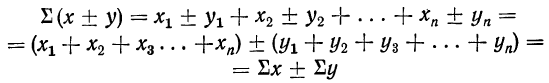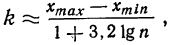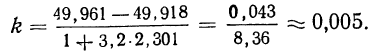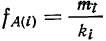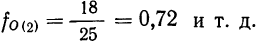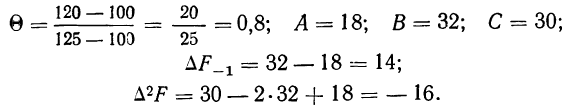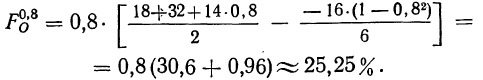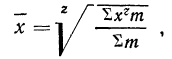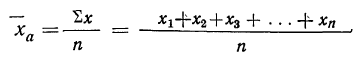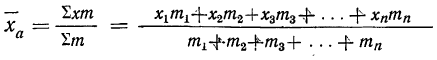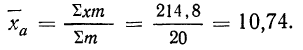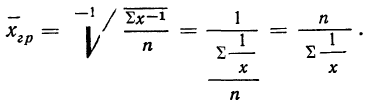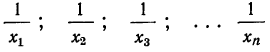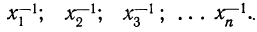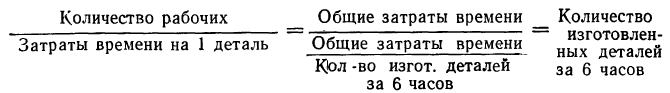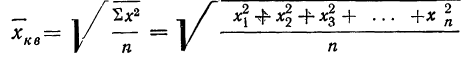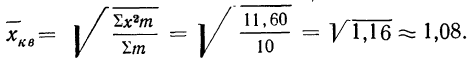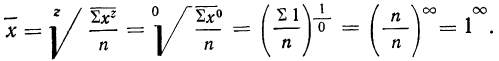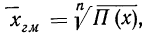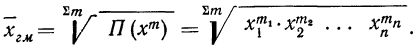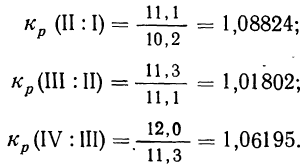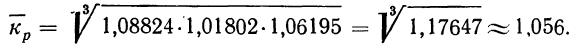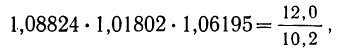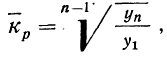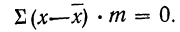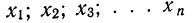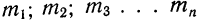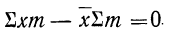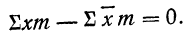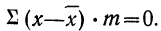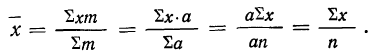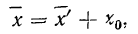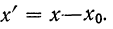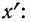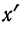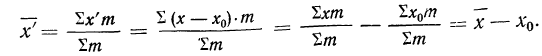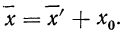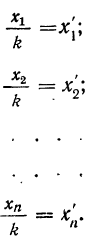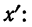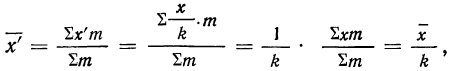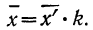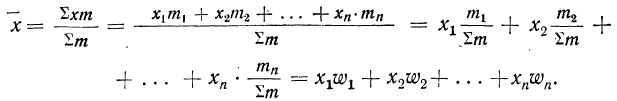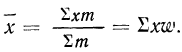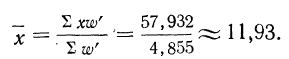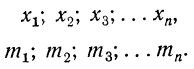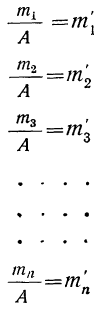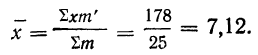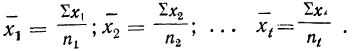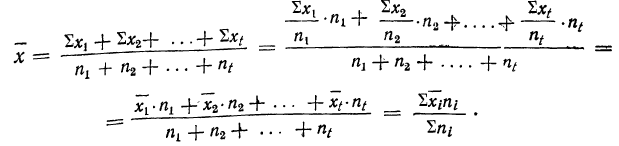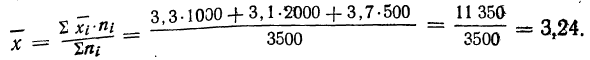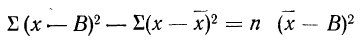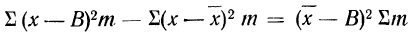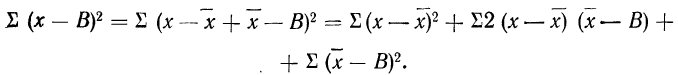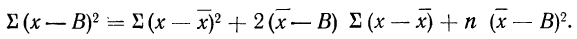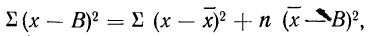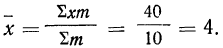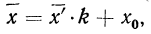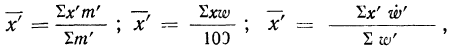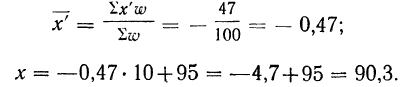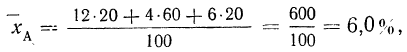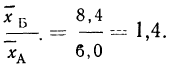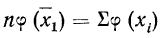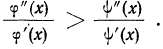что означает вариационный ряд

Вариационный ряд

Смотреть что такое «Вариационный ряд» в других словарях:

ВАРИАЦИОННЫЙ РЯД — последовательность значений наблюденной величины, расположенных в порядке возрастания. Напр., вариационный ряд значений 1, 3, 0, 5, 3, 4 имеет вид 3, 0, 1, 3, 4, 5 … Большой Энциклопедический словарь

ВАРИАЦИОННЫЙ РЯД — англ. variation distribution; нем. Variationreihe. Совокупность к. л. величин, расположенных в порядке их возрастания; полностью определяется указанием различных значений, входящих в него величин и числа членов ряда. см. СТАТИСТИКА. Antinazi.… … Энциклопедия социологии

вариационный ряд — упорядоченная выборка — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы упорядоченная выборка EN set of variate values … Справочник технического переводчика

вариационный ряд — последовательность значений наблюдаемой величины, расположенных в порядке возрастания. Например, вариационный ряд значений 1, –3, 0, 5, 3, 4 имеет вид –3, 0, 1, 3, 4, 5. * * * ВАРИАЦИОННЫЙ РЯД ВАРИАЦИОННЫЙ РЯД, последовательность значений… … Энциклопедический словарь

ВАРИАЦИОННЫЙ РЯД — Упорядоченное изображение реально существующего распределения особей в группе по величине признака. Вариационный ряд это двойной ряд чисел, состоящий из обозначения классов и соответствующих частот. Показывает, как изменяется признак от… … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных

вариационный ряд — variacinė eilutė statusas T sritis augalininkystė apibrėžtis Bet kurio kiekybinio požymio didėjimo ar mažėjimo tvarka išdėstyti variantai. atitikmenys: angl. variational series rus. вариационный ряд … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas

вариационный ряд — 3.3 вариационный ряд: Совокупность значений варьирующего признака [8]. Величина интервала (интервальная разность) разность между верхними и нижними границами интервала [8]. Источник: Р 52.24.661 2004: Оценка риска антропогенного воздейс … Словарь-справочник терминов нормативно-технической документации

ВАРИАЦИОННЫЙ РЯД — расположение значений случайной выборки с функцией распределения в порядке их возрастания: В. р. служит для построения эмпирич. функции распределения где число членов ряда, меньших х. Важными характеристиками В. р. являются его крайние члены и… … Математическая энциклопедия

ВАРИАЦИОННЫЙ РЯД — последовательность значений наблюдаемой величины, расположенных в порядке возрастания. Напр., В. р. значений 1, 3, 0, 5, 3, 4 имеет вид 3, 0, 1, 3, 4, 5 … Естествознание. Энциклопедический словарь

Источник

Вариационные ряды

Главная > Учебные материалы > Математика: Вариационные ряды

1.Вариационный ряд. 2.Числовые характеристики вариационного ряда.

1.Вариационный ряд.

Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.

Таб.1

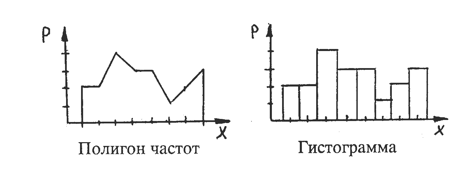
По данным таблицы построим полигон распределения частот (рис.1)

В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.

Таб. 2

По данным таблицы построим гистограмму распределения частот (рис.2)

Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.

2.Числовые характеристики вариационного ряда.

Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости.

Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической.

Дисперсией s 2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической.

Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии.

Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака.

Пример.

В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины.

Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен.

Как видно из таблицы сумма произведений x i n i = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда.

По данным таблицы построим гистограмму распределения частот.

Построим и эмпирическую функцию распределения случайной величины (кумуляту).

Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:

Источник

Вариационный ряд и методика его составления

Средние величины рассчитываются на основе вариационных рядов.

Вариационный ряд — это однородная в качественном отношении статистическая совокупность, отдельные единицы которой характеризуют количественные различия изучаемого признака или явления.

Цифровое значение, каждого отдельного признака или явления, входящего в вариационный ряд, называется вариантой и обозначается буквой V. Числа, показывающие, как часто встречается та или иная варианта в составе данного ряда, носят названия частот и обозначаются буквой — р. Общее число случаев наблюдений, из которых вариационный ряд состоит, обозначают буквой n.

Варианты, расположенные в порядке возрастания или убывания количественной характеристики признака, составляют ранжированный вариационный ряд.

Вариационный ряд
I Виды вари­а­ционных рядов	Простой	Сгруппирован­ный
II Характеристика вари­ационного ряда	Варианта V	Частота p	Общее число наблюдений n
III Этапы составления сгруппированного ряда	Опреде­ле­ние числа групп	Опреде­ление интервала	Определение границ и середины группы	Распределение наблюдений по группам	Графическое изображение
IV Практи­ческое применение	Для характеристики типа распределения признака в совокупности	Для вычисления среднего уровня (средней величины)

Различают два вида вариационных рядов:

— простой вариационный ряд;

— сгруппированный вариационный ряд,

Простым вариационным рядом называется такой ряд, где каждая варианта встречается лишь один раз. Вариационный ряд, где указано сколько раз встречается каждая варианта называется сгруппированным вариационным рядом.

Если исследователь имеет не более 30 наблюдений, то достаточно все значения признака расположить в нарастающем или в убывающем порядке (от минимальной варианты до максимальной или наоборот) и указать частоту каждой варианты. При большом числе наблюдений (более 30) рекомендуется варианты объединить в группы с указанием частоты встречаемости всех вариант, входящих в данную группу.

Основные требования к составлению вариационного ряда:

1. Расположить все варианты по порядку

2. Суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой единицы

3. Определить количество групп

4. Определить интервал между группами

5. Определить начало, середину и конец группы

6. Распределить данные наблюдений по группам

7. Графические изобразить вариационный ряд

Методику построения сгруппированного вариационного ряда рассмотрим на следующем примере:

Даны данные о частоте пульса (число ударов в минуту) у 54 студентов перед экзаменом: 60, 70, 70, 68, 70, 72, 64, 66, 66, 70, 76, 76, 80, 64, 6.2, 78, 78, 76, 70, 68, 64, 62, 70, 68, 72, 70, 72, 72, 70, 70, 76, 76, 76 74, 74, 74, 80, 80, 66, 72, 76, 76, 74, 74, 74, 72, 78, 78, 76, 74, 76, 76, 80, 78.

1. Строим вариационный ряд, последовательно располагая варианты в порядке возрастания: 60, 62, 62, 64, 64, 64, 66, 66, 66, 68, 68, 68, 70, 70, 70, 70, 70, 70, 70, 70, 70, 72, 72, 72, 72, 72, 72,74, 74, 74, 74, 74, 74, 74,76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 76, 78, 78, 78, 78, 78, 80, 80, 80, 80.

2. Распределение студентов в зависимости от частоты пульса перед экзаменом

частота пульса (V)

число студентов (p)

Всего студентов n =54

3. Определение количества групп.

Количество групп в вариационном ряду находим в специально разработанной таблице.

Число вариант (n)	31–45	46–101	101–200	201–500
Число групп (р)	6–7	8–10	11–12	13–17

В нашем примере число наблюдений — 54, поэтому в вариационном ряду следует иметь 8 групп.

3. Определение величины интервала (i) между группами. Интервал между группами определяют по формуле:

i=	Vmax–Vmin	=	80–60	=	=2,5
r (число групп)

Полученный интервал 2,5 рекомендуется округлять до целого числа — 3.

6. Разбиваем весь ряд на группы используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда

частота пульса (V)	середина группы вариант	число студентов
60–62
63–65
66–68
69–71
72–74
75–77
78–80
n = 54

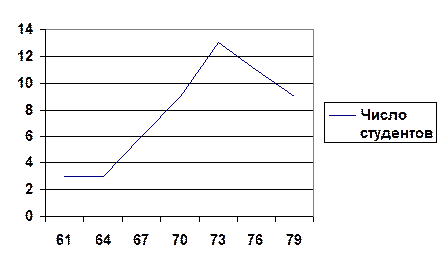
7. Строим графическое изображение вариационного ряда (по серединам групп)

Распределение студентов по частоте пульса перед экзаменом

Полученный ряд распределения (вариационный ряд) и графическое его изображение делают статистические данные обозримыми, доступными для анализа и дальнейшего изучения.

Источник

Вариационные ряды — помощь в оценке распределения явлений по величине признаков

Вариационный ряд (frequency table)- ранжированный ряд распределения по величине какого-либо признака. Этот признак носит название варьирующего, а его отдельные числовые значения называются вариантами и обозначаются через «х». Число, показывающее, сколько раз данная варианта встречается в вариационном ряду, называется частотой и обозначается через «р».

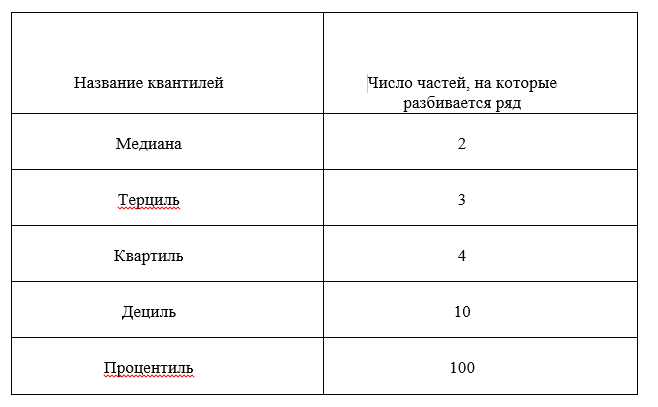
Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями (quantile). Наиболее часто употребляемые квантили представлены в таблице:

Рис. 1 Этапы описания (обобщения) количественного признака

Виды вариационных рядов

Вариационные ряды могут быть следующих видов:

Графическое изображение вариационных рядов

где х — варианты, р — частоты.

Основные характеристики вариационного ряда

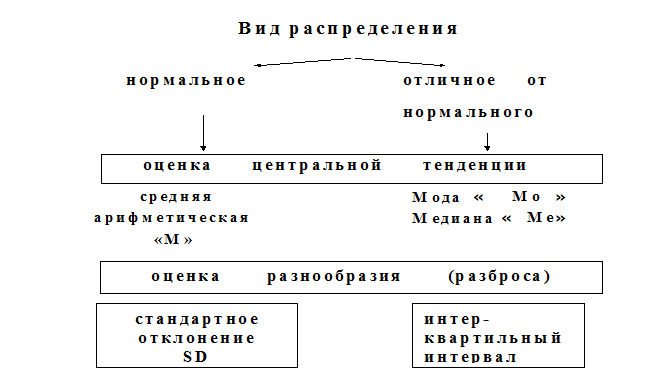
Такие характеристики зависят от оцениваемых показателей:

1). Показатели, характеризующие центральную тенденцию (central tendency) или уровень ряда: средние величины или меры расположения (собственно средние и структурные средние).

2). Показатели, характеризующие разнообразие (рассеяние, вариацию, разброс) (spread) признака: стандартное отклонение, дисперсия, размах, интерквартильный интервал.

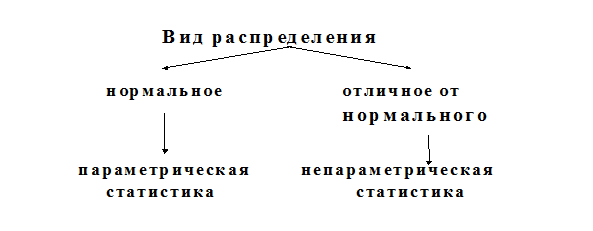
Выбор характеристик центральной тенденции и разнообразия признака прежде всего зависит от вида распределения. В случае нормального распределения используют показатели параметрической статистики, в случае распределения, отличного от нормального и при неизвестном виде распределения применяют показатели непараметрической статистики.

Средние величины

Средняя величина — обобщающий коэффициент, который характеризует наиболее типичный размер определенного признака в целом для совокупно­сти или для отдельных ее частей. Расчет средних величин имеет смысл только для качественно однородной совокупности, в связи с этим в одной совокупности может быть столько средних, на сколько однородных групп она может быть разбита.

Виды средних величин

Средняя арифметическая(mean) — применяется, если варианты возрастают (убывают) в арифметической прогрессии.

х — средняя арифметическая;

р — частота встречаемости варианты;

n — число наблюдений

Свойства средней арифметической:

— носит обобщающий характер;

— имеет абстрактное значение;

— алгебраическая сумма отклонений отдельных вариант от средней равна 0 (сущность средней и способ проверки правильности расчета средней);

— сумма квадратов отклонений отдельных вариант от средней меньше суммы квадратов отклонений вариант от любой другой величины, неравной средней;

— сумма произведений отдельных вариант на свои частоты равна произведению средней на число наблюдений (единство суммарного действия и способ провер­ки правильности расчета средней);

— если частоту всех вариант пропорционально изменить, то средняя арифметическая от этого не изменится.

Средняя геометрическая — вычисляется, если варианты возрастают (убыва­ют) в геометрической прогрессии.

На практике используют логарифмированную формулу:

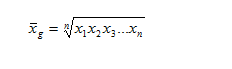
Структурные средние

Мода (Мо) (mode)- наиболее часто встречающаяся в вариационном ряду варианта.

Медиана (Me)(median) — варианта, которая делит вариационный ряд на две равные

части. Медиана используется:

Характеристики разнообразия вариационного ряда

— приблизительный расчет стандартного отклонения по амплитуде:

где К — коэффициент Ермолаева, рассчитывается по специальной таблице с учетом числа наблюдений (см. приложение).

При числе наблюдений больше 30:

Стандартное отклонение наиболее часто используется при определении нормы и патологии, в основе которого лежит «правило трех сигм», справедливое только для нормального распределения.

Сводная таблица формул

для нахождения средних значений и мер рассеяния

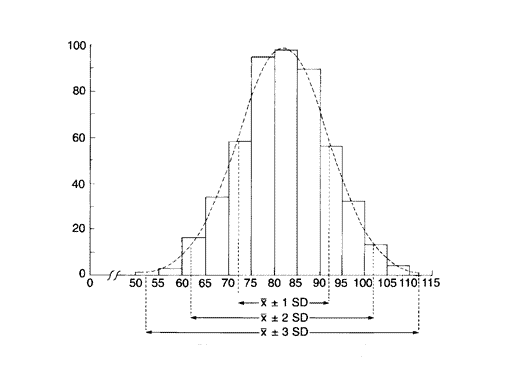
«Правило трех сигм»

68.3 % всех вариант отклоняются от своей средней не более, чем на s

95.4% вариант находятся в пределах X ± 2s

99.7% вариант находятся в пределах X ± 3s

Отклонение параметра от его средней арифметической в пределах s расценивается как норма, субнормальным считается отклонение в пределах ± 2s и патологическим — сверх этого предела, т.е. > ± 2s» (рис. )

Рис.3 Правило «трех сигм» ( SD – стандартное отклонение).

При распределении Пуассона дисперсия равна средней:

Коэффициент вариации используется при сравнении вариационных рядов, имеющих различную размерность, или одной размерности, но обладающими резкими различиями в своих значениях, затрудняющими их сопоставление.

Вариационный ряд разбивают на четыре интервала, получая, соответственно, 25%, 50% и 75% квантили; 25% и 75% квантили называют также нижним (low quartile) и верхним квартилями(high quartile). 50% квантиль – это медиана. Внутри интерквартильного интервала (между 25% и 75% квантилями) лежат 50% наиболее типичных (близких к центральному) значений.

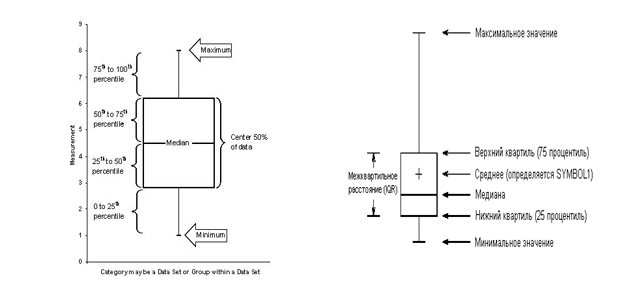
Таким образом, в случае нормального распределения вариационный ряд описывается средней величиной и стандартным отклонением, если распределение неизвестно или оно отлично от нормального, центральную тенденцию и разброс можно описать с помощью медианы, нижнего и верхнего квартиля (интерквартильным интервалом).

Рис.4 Графическое представление описательной статистики (коробчатый график, «коробка с усами», box-plot)

Проверка нормальности распределения

Соответствие экспериментального распределения нормальному проверяется следующими способами:

х ± 0.3 s находится 25 % всех единиц наблюдения;

х ± 0.7 s находится 50 % всех единиц наблюдения;

х ± l,l s находится 75 % всех единиц наблюдения;

х ± 3,0 s находится 99 % всех единиц наблюдения.

— при нормальном распределении, которое обладает симметричностью:

— правило «двух третей» Юла:

а). если распределение симметрично: Me = Mo;

б). если распределение обладает правосторонней асимметрией: Me > Mo;

в). если распределение имеет левостороннюю асимметрией Me 0

в) при левосторонней асимметрии: A _s s × f, то «выскакивающая» варианта исключается из исследования;

Источник

Содержание:

В результате статистической обработки материалов, полученных при измерении величины явления, можно подсчитать число единиц, обладающих конкретным значением того или иного признака.

Условились каждое отдельное значение признака обозначать

Если мы расположим отдельные значения признака (варианты) в возрастающем или убывающем порядке и укажем относительно каждого варианта, как часто он встречался в данной совокупности, то получим распределение признака, или вариационный ряд.

Вариационные ряды и их характеристики

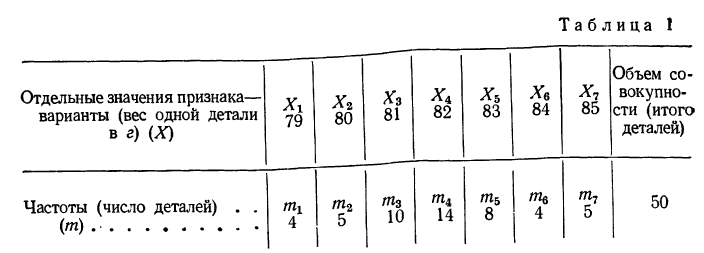
Построим вариационный ряд для приведенного выше примера. Для этого находим наименьший вариант, равный 79 г, и, располагая варианты в возрастающем порядке, подсчитываем их частоту. Так, вариант 79 г встречается 4 раза, вариант 80 г — 5 раз и т. д. Расположим полученные варианты следующим образом (см. табл. 1).

Такой ряд называется вариационным рядом; он характеризует изменение (варьирование) какого-нибудь количественного признака (в нашем примере варьирование веса деталей). Следовательно, вариационный ряд представляет собой две строки (или колонки). В одной из них приводятся варианты, а в другой частоты.

Виды вариации

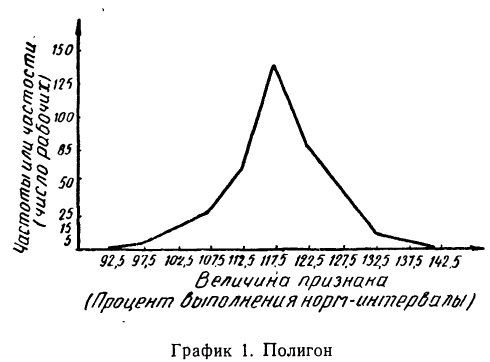
Вариация признака может быть дискретной и непрерывной. Дискретной вариацией признака называется такая, при которой отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число), т. е. даны в виде прерывных чисел. Непрерывной называется вариация, при которой значения признака могут отличаться одно от другого на сколь угодно малую величину. В качестве примера можно привести: для дискретной вариации признака — число станков, обслуживаемых одним рабочим, число семян в 1 кг и т. д.; для непрерывной вариации признака— процент выполнения рабочим нормы выработки, вес одного семени и т. д.

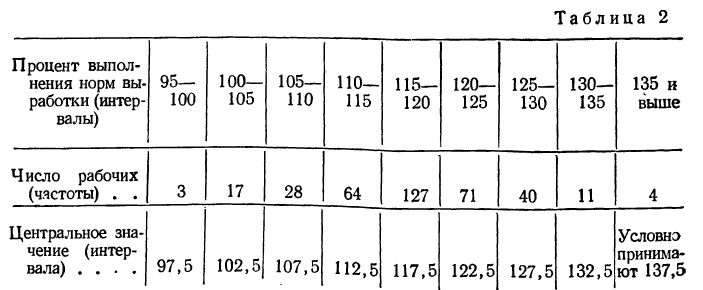
При непрерывной вариации распределение признака называется интервальным. Частоты относятся не к отдельному значению признака, как это бывает при дискретной вариации, а ко всему интервалу. Часто за значение интервала принимают его середину, т. е. центральное значение. В качестве примера можно привести интервальный вариационный ряд по проценту выполнения норм выработки.

Пример 1.

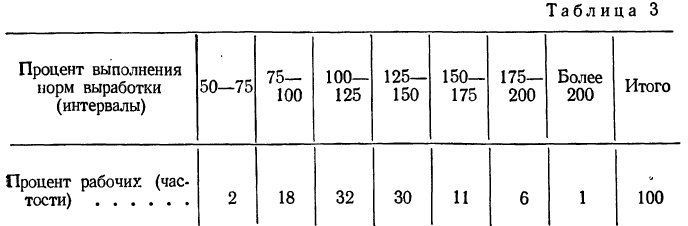
Распределение рабочих по проценту выполнения норм выработки.

Частость

Нередко вместо абсолютных значений. частот используют относительные величины. Для этой цели можно использовать долю частоты того или иного варианта (а также интервала) в сумме всех частот. Такая величина называется частостью и обозначается

Мы имеем частоты

Для получения суммы всех частот их нужно сложить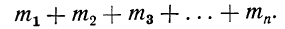

В математике используется знак 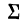(греческая буква сигма заглавная), означающий суммирование.

Следовательно, можно записать: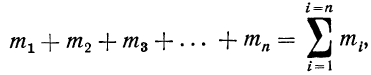

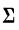
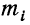
где значки 1=1 и i=n под и над показывают, что суммированию подлежат все при условии, что i принимает все целые значения от 1 до n.

В дальнейшем в подобных случаях (т. е. при суммировании по подстрочному номеру i) мы не будем записывать значения, принимаемые i, но будем помнить смысл записи 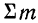(уже без указания значений, принимаемых i).

Для получения частости каждого варианта или интервала-нужно его частоту разделить на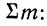
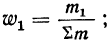
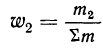
и т.д.,
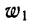
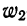
где — частость первого варианта или интервала, — второго и т. д.

Вычислим частости, используя данные табл. 1:

Сумма всех частостей равна 1:

В нашем примере
0,08+0,1+0,2+0,28+0,16+0,08+0,1 = 1,00.
Частости можно выражать и в процентах (тогда сумма всех частостей равна 100%).

Границы интервалов

В интервальном вариационном ряду в каждом интервале различают нижнюю и верхнюю границы интервала:

При построении интервальных вариационных рядов в каждый интервал включаются варианты, числовые значения которых больше нижней границы и меньше или равны верхней грани це. Так, в табл.12 в интервал 95—100% попадают все рабочие, выполнившие нормы выработки от 95 до 100% включительно. Рабочие, выполнившие план на 100,01%, попадают в следующий интервал. Разумеется надо стремиться строить интервалы так, чтобы избегать попадания значительного числа случаев на границы интервалов.

Интервальные вариационные ряды бывают с одинаковыми и неодинаковыми интервалами. В последнем случае чаще всего встречаются интервалы последовательно увеличивающиеся.

Пример 2.

Вариационный ряд с равными интервалами:

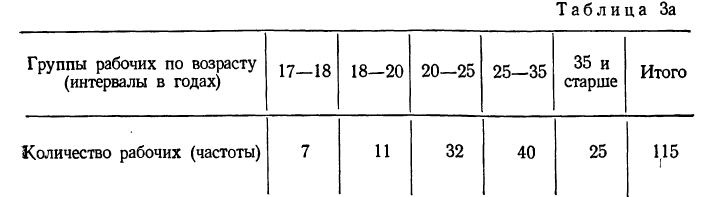
Пример 2а.

Вариационный ряд с последовательно увеличивающимися интервалами:

Свойства сумм

Как видно (и из дальнейшего изучения материала), нам приходится иметь дело с суммами. Рассмотрим некоторые свойства сумм.

1) Сумма ограниченного числа слагаемых, имеющих одну и ту же величину (сумма постоянной), равна произведению величины слагаемых на их число:

2) Постоянный множитель может быть вынесен из-под знака суммы и введен под знак суммы:

3) Сумма алгебраической суммы нескольких переменных равна алгебраической сумме сумм каждой переменной:

(легко обобщается на большее число слагаемых).

Величина интервала

Для выбора оптимальной величины интервала, т. е. такой величины интервала, при которой вариационный ряд не будет очень громоздким и в нем не исчезнут особенности явления, можно рекомендовать формулу:

где n — число единиц в совокупности.

Так, если в совокупности 200 единиц наибольший вариант равен 49,961, а наименьший — 49,918, то

Следовательно, в данном случае оптимальной величиной интервала может служить величина 0,005.

Плотность распределения

В качестве характеристики ряда распределения применяют плотность распределения, которую вычисляют как отношение-частот или частостей к величине интервала.

Различают абсолютную плотность распределения:

и относительную плотность распределения: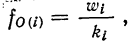

где 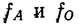-— плотности распределения, абсолютная (со значком А) и относительная (со значком О).

Пример 3.

По данным примера 2 вычислим относительную плотность распределения. Для первого интервала

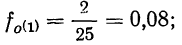
для второго интервала

Расщепление интервалов

Часто возникает необходимость в расщеплении интервалов. Для этой цели можно воспользоваться следующим методом для интервальных вариационных рядов с равными интервалами.

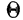
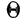
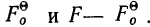
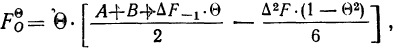
Расщепление производится при предположении, что плотность вариационного ряда изменяется по параболе второго порядка. Имеется в виду, что весь интервал разбивается на две части: первую, составляющую долю в величине интервала, и вторую 1—. Соответственно частость расщепляемого интервала F распадается на В этом случае:

где А — частость интервала, предшествующего расщепляемому;

В — частость расщепляемого интервала;

С — частость интервала, последующего за расщепляемым;

— приращение частости интервала, предшествующего расщепляемому ();

— второе приращение частостей — (В—А)=С—2В+А].

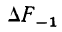
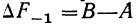
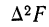
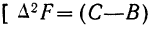
Пример 4.

По данным примера 2 произведем расщепление интервала 100—125% на две части, выделим часть интервала 100—120% и определим удельный вес рабочих, выполняющих норму выработки от 100 до 120%.

Имеем:

Получаем частость по соответствующей формуле:

В случае неравных интервалов вычисление усложняется.

Графические методы изображения вариационных рядов

Большое значение для наглядного представления вариационного ряда имеют графические методы его изображения. Вариационный ряд графически может быть изображен в виде полигона, гистограммы, кумуляты и огивы.

На оси абсцисс отмечаются точки, соответствующие, величине вариантов, и из них восстанавливаются ординаты (перпендикуляры), длина которых соответствует численности этих вариантов. Вершины ординат соединяются прямыми линиями. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но могут быть применены и для интервальных рядов. В этом случае ординаты, пропорциональные частоте или частости интервала, восстанавливаются перпендикулярно оси абсцисс в точке, соответствующей середине данного интервала. Для замыкания крайние ординаты соединяются с •серединой интервалов, в которых частоты или частости равны нулю.

Пример 5.

По данным примера 1 строим полигон.

Гистограмма распределения строится аналогично полигону в прямоугольной системе координат. В отличие от полигона при построении гистограммы на оси абсцисс берутся не точки, а отрезки, изображающие интервал, а вместо ординат, соответствующих частотам или частостям отдельных вариантов, строят прямоугольники с высотой, пропорциональной частотам или частостям интервала.

В случае неравенства интервалов гистограмма распределения строится не по частотам или частостям, а по плотности интервалов (абсолютной или относительной). При этом общая площадь гистограммы равна численности совокупности, если построение производится по абсолютной плотности, или единице, если гистограмма построена по относительной плотности.

Если соединить прямыми линиями середины верхних сторон прямоугольников, то получим полигоны распределения.

Разбивая интервалы на несколько частей и исходя из того, что вся площадь гистограммы должна остаться при этом неизменной, можно получить мелкоступенчатую гистограмму, которая в пределе (за счет уменьшения величины интервала) перейдет в плавную кривую, называемую кривой распределения.

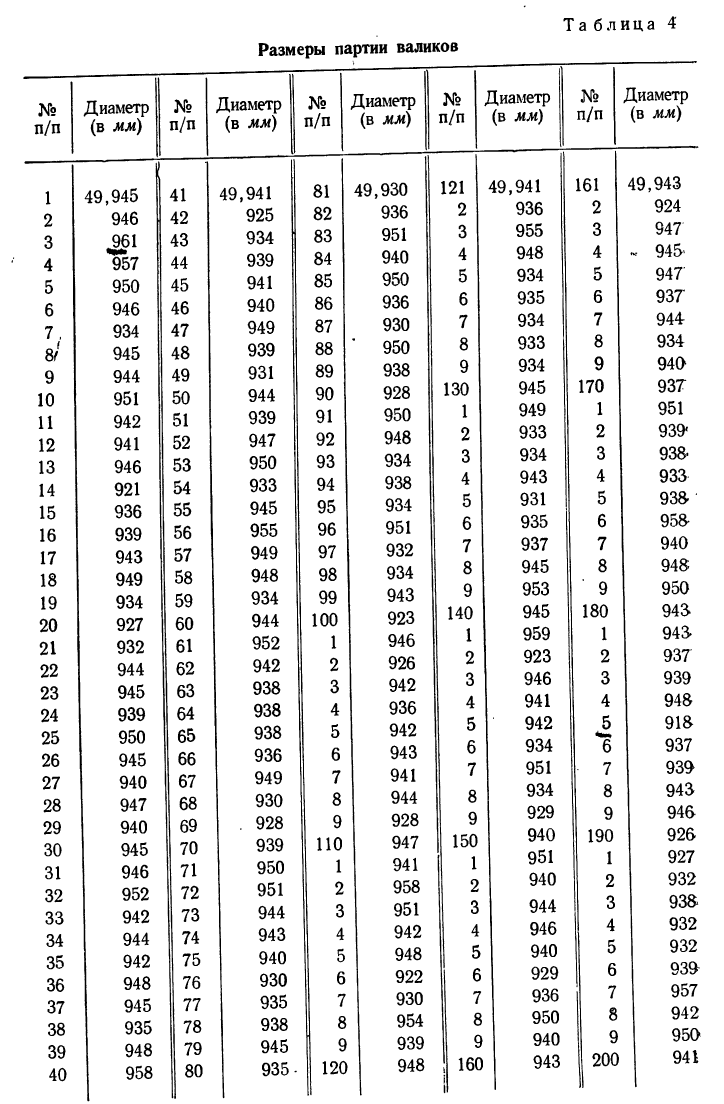
Пример 6.

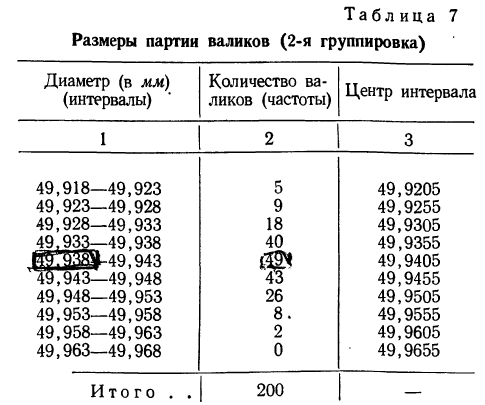
Имеются данные о диаметре 200 валиков (см. табл. 4).

Чтобы по этим данным построить вариационный ряд с равными интервалами, изобразить его с помощью гистограммы, а затем превратить ее в мелкоступенчатую, производим следующие действия:

а) Выбираем наименьший вариант, а затем наибольший и находим между ними разность. Делим полученную разность на число проектируемых интервалов и получаем величину каждого интервала.

Так, наименьший интервал 49,918, наибольший — 49,961. Разность 49,961—49,918=0,043.

Допустим, мы хотим получить пять интервалов, тогда величина каждого интервала равна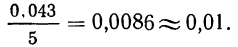

Следовательно, будем иметь такие интервалы:

49,918—49,928; 49,928—49,938 и т. д.

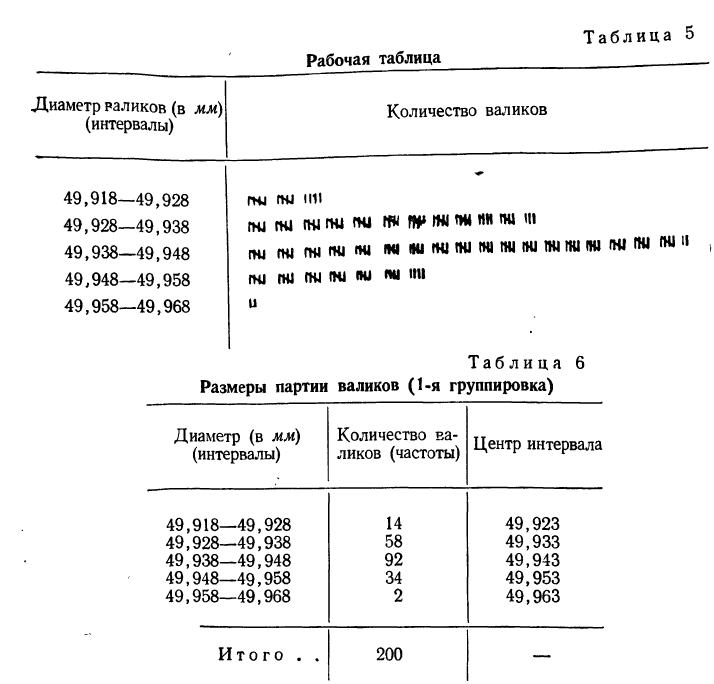
На основании рабочей таблицы получаем следующий вариационный ряд (см. табл. 6).

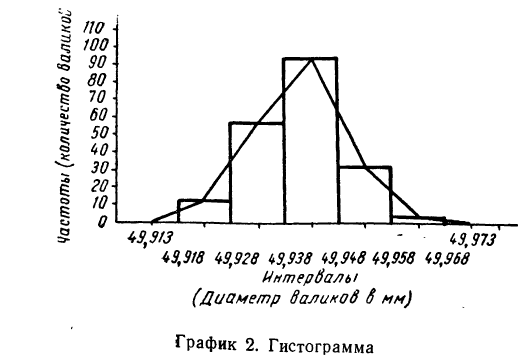
б) По полученному вариационному ряду строим гистограмму распределения: на оси абсцисс откладываем диаметры валиков, начиная с 49,918 до 49,968, а на оси ординат проставляем масштаб; далее строим прямоугольники с высотой, пропорциональной количеству валиков в каждом интервале.

Соединяем прямыми линиями середины верхних сторон прямоугольников и получаем полигон (см. график 2).

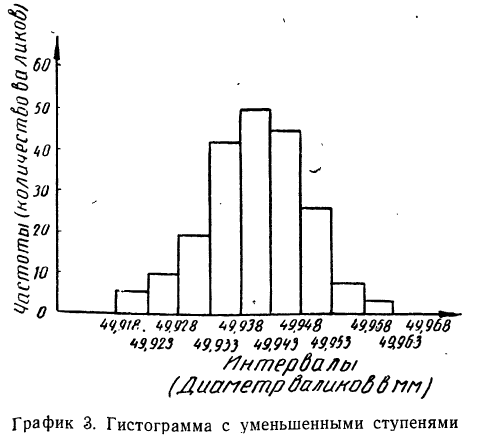
Для получения мелкоступенчатой гистограммы разбиваем интервалы на две равные части и получаем:

Если построить гистограмму по новому вариационному ряду, с уменьшенными интервалами, то получим гистограмму с более мелкими ступенями. Учет требования о неизменности площади гистограммы приводит к необходимости увеличить масштаб оси ординат вдвое.

Можно продолжить процесс расчленения интервалов и дальше, получая все более и более мелкоступенчатую гистограмму.

Кумулятивная кривая (кривая сумм — кумулята) получается при изображении вариационного ряда с накопленными частотами или частостями в прямоугольной системе координат. При построении кумуляты дискретного признака на ось абсцисс наносятся значения признака (варианты). Ординатами служат вертикальные отрезки, длина которых пропорциональна накопленной частоте или частости того или иного варианта. Соединением вершин ординат прямыми линиями получаем ломаную (кривую) кумуляту.

Пример 7.

По данным табл. 4 построить кумуляту.

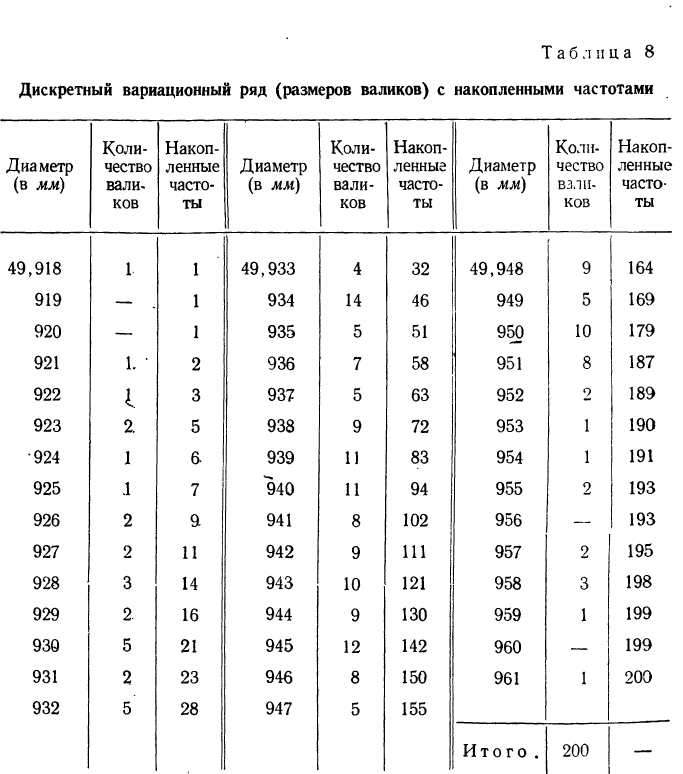
Составляем дискретный вариационный ряд с накопленными частотами (при наличии частостей можно для построения кумуляты пользоваться ими; см. табл. 8).

Накопленная частота определенного варианта получается суммированием всех частот вариантов, предшествующих данному, с частотой этого варианта.

Используя накопленные частоты, строим кумуляту.

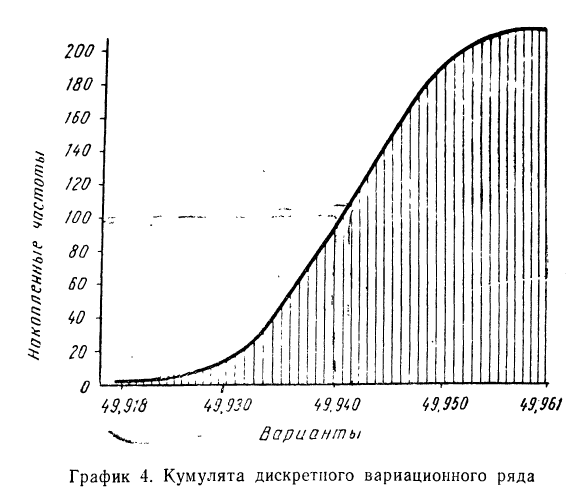
При построении кумуляты- интервального вариационного ряда нижней границе первого интервала соответствует частота, равная нулю, а верхней границе — вся частота интервала. Верхней границе второго интервала соответствует накопленная частота первых двух интервалов (т. е. сумма частот этих интервалов) и т. д. Верхней границе последнего (максимального) интервала соответствует накопленная частота, равная сумме всех частот.

Пример 8.

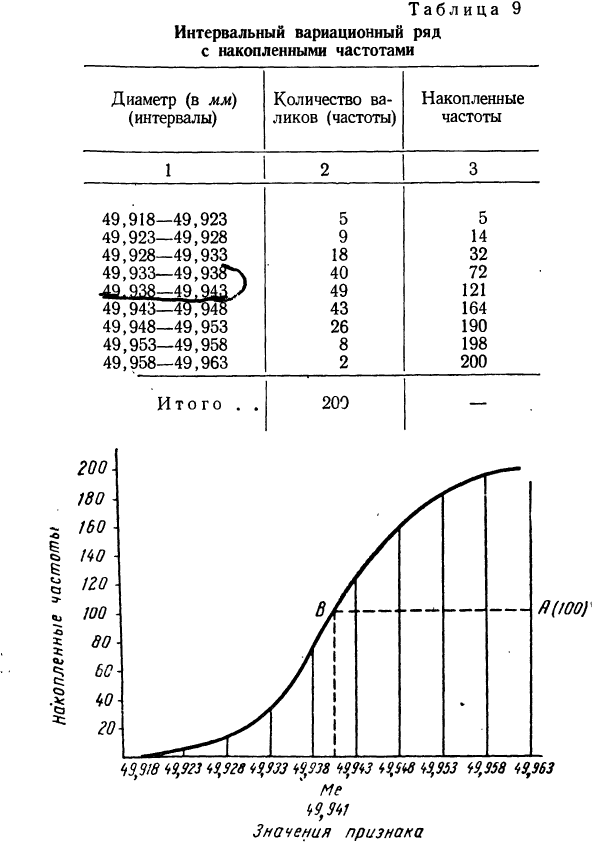
По данным табл. 7 построить кумуляту.

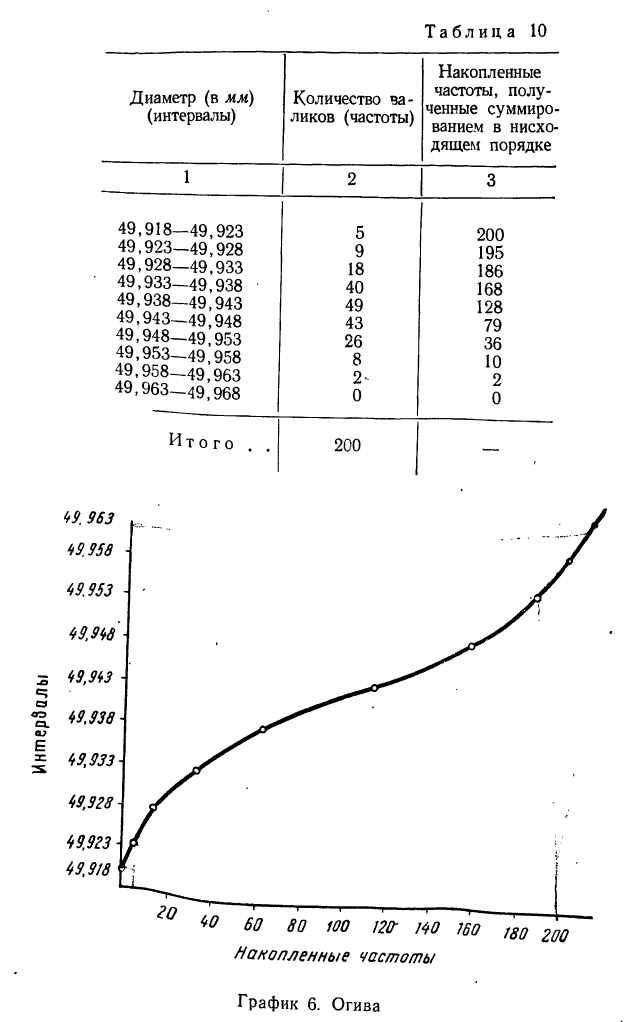
Составляем интервальный вариационный ряд с накопленными частотами (см. табл. 9). По полученным накопленным частотам строим кумуляту (см. график 5).

Огива строится аналогично кумуляте с той лишь разницей, что на ось абсцисс наносят накопленные частоты, а на ось ординат — значения признака. Если лист бумаги, на котором изображена кумулята, повернуть на 90° и посмотреть на него с обратной стороны на свет, то можно увидеть огиву.

График 5. Кумулята интервального вариационного ряда

Пример 9. По данным табл. 9 построим огиву (см. график 6)-

Накопленные частоты можно получать не только в восходящем порядке, но и в нисходящем, тогда частоты вариантов суммируются снизу вверх.

Пример 10.

По данным табл. 7. вычислить накопленные частоты в нисходящем порядке.

Средние величины

В качестве одной из важнейших характеристик вариационного ряда применяют среднюю величину. Математическая статистика различает ряд типов средних величин: арифметическую, геометрическую, гармоническую, квадратическую, кубическую и др. Все перечисленные типы средних могут быть исчислены для случаев, когда каждый из вариантов вариационного ряда встречается только один раз, — тогда средняя называется простой или невзвешенной, — и для случаев, когда варианты или интервалы повторяются различное число раз. При этом число повторений вариантов или интервалов называют частотой или статистическим весом, а среднюю, вычисленную с учетом статистического веса, —взвешенной средней.

Выбор одного из перечисленных типов средних для характеристики вариационного ряда производится не произвольно, а в зависимости от особенностей изучаемого явления и цели, для которой средняя исчисляется.

Практически при выборе того или другого типа средней следует исходить из принципа осмысленности результата при суммировании или при взвешивании. Только тогда средняя применена правильно, когда в результате взвешивания или суммирования получаются величины, имеющие реальный смысл.

Обычно затруднения при выборе типа средней возникают лишь в использовании средней арифметической или гармонической. Что же касается геометрической и квадратической средних, то их применение ограничено особыми случаями (см. далее).

Степенная средняя

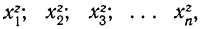
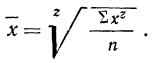
Все указанные типы средних величин могут быть получены из формул степенной средней. Если имеются варианты то средняя из вариант тов может быть исчислена по формуле простой невзвешенной степенной средней порядка z

При наличии соответствующих частот 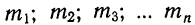средняя исчисляется по формуле взвешенной степенной средней

где 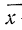— степенная средняя;

z — показатель степени, определяющий тип средней;

m — частоты или статистические веса вариантов.

Средняя арифметическая получается из формулы степенной средней при подстановке z=1

средняя арифметическая невзвешенная и

средняя арифметическая взвешенная.

Пример 11.

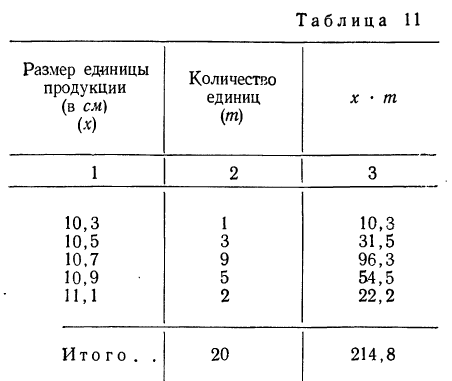
Измерения 20 единиц продукции дали следующие результаты (колонки 1 и 2):

Вычислить средний размер единицы продукции.

Находим среднюю арифметическую. Для этого исчисляем в табл. 11 колонку 3

Здесь умножение значения признака на вес и суммирование этих произведений дает общий размер продукции, т. е. имеет реальный смысл.

Средняя гармоническая получается при подстановке в формулу степенной средней значения z =—1.

Средняя гармоническая простая

Средняя гармоническая взвешенная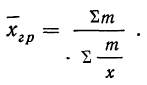

Средняя гармоническая вычисляется в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, т. е. когда суммированию подлежат не сами варианты, а обратные им величины

Пример 12.

По следующим данным о работе 22 рабочих в течение 6 часов вычислить среднюю гармоническую взвешенную.

В данном случае взвешивание состоит в делении по каждой группе количества рабочих (m) на затраты времени по изготовлению одной детали (х). Для проверки правильности выбора типа средней осмыслим результат взвешивания. Исходя из того, что все рабочие работали по 6 часов, количество рабочих можно рассматривать как величину, определяющую общие затраты времени. Тогда результат деления представит вполне осмысленную величину:

Таким образом, средняя гармоническая в данном примере применена правильно. При использовании средней гармонической для упрощения расчетов целесообразно пользоваться таблицами обратных чисел (см. приложение VIII).

Средняя квадратическая получается из формулы степенной средней при подстановке z=2

средняя квадратическая невзвешенная и

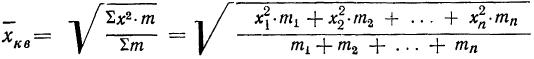
средняя квадратическая взвешенная.

Средняя квадратическая используется только в тех случаях, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы.

Пример 13.

Имеются результаты измерения отклонений фактической длины изделий от заданной нормы.

Вычислим среднюю величину отклонений.

Находим среднюю квадратическую взвешенную; для этого исчисляем в табл. 13 колонки 3 и 4:

Значит, средняя величина отклонений фактической длины изделий от заданной нормы составляет 1,08 мм. В данном случае средняя арифметическая была бы непригодна, так как в результате мы получили бы нуль

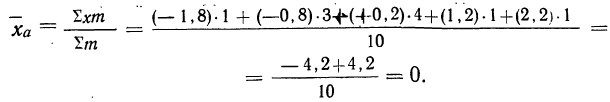
Средняя геометрическая получается из формулы степенной средней при подстановке z=0:

Для раскрытия неопределенности этого вида прологарифмируем обе части равенства: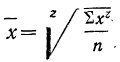

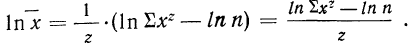
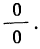
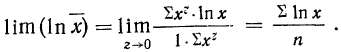
Теперь при подстановке z в правую часть равенства получаем неопределенность вида Используя правило Лопиталя и дифференцируя отдельно числитель и знаменатель по переменной z, получаем:

Таким образом:

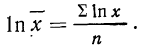
Потенцируя, находим среднюю: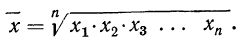

Это и есть формула средней геометрической невзвешенной, которая записывается сокращенно так:

где П — знак произведения;

n — число вариантов.

Если использовать частоты (m), то средняя геометрическая взвешенная примет следующий вид:

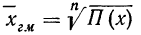
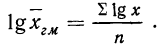
Вычисления средней геометрической в значительной мере упрощаются применением логарифмирования. Для невзвешенной средней геометрической получаем:

Для взвешенной средней геометрической: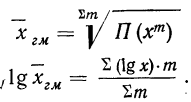

Таким образом, логарифм средней геометрической есть средняя арифметическая, из логарифмов вариантов (см. формулы средней арифметической).

Средняя геометрическая используется главным образом при изучении динамики (см. раздел II).

Расчет средних коэффициентов и темпов. роста производится по формулам средней геометрической.

Пример 14.

Выпуск промышленной продукции производился предприятием в следующих размерах:

Чтобы найти средний месячный коэффициент и темп роста промышленной продукции, определяем помесячные коэффициенты роста 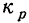, которые в данном случае и являются вариантами:

Из найденных трех помесячных коэффициентов роста (вариантов) определяем средний месячный коэффициент роста 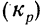по формуле средней геометрической. Для этого найденные коэффициенты роста перемножаются и из произведения извлекается корень третьей степени

Из разобранного примера можно сделать два вывода: во-первых, что произведение трех найденных коэффициентов роста можно получить без их предварительного исчисления путем деления апрельского объема продукции (12,0) на январский объем (10,2):

и, во-вторых, что показатель степени корня, равный трем (число коэффициентов роста), можно получить вычитанием единицы из числа приведенных в примере месяцев (четыре).

Таким образом, наиболее удобной для исчисления среднего коэффициента роста следует считать формулу:

где n — число приведенных дат или периодов;

— последний член ряда;

— первый член ряда.

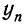
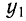
Математические свойства средней арифметической

Из вышеуказанных средних наиболее часто применяется средняя арифметическая. Знание свойств средней арифметической позволяет упрощенно ее вычислять.

Математические свойства средней арифметической:

1) Средняя постоянной величины равна этой же постоянной

2) Сумма отклонений от средней, умноженных на веса (частоты), равна нулю:

(если все веса равны единице)
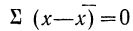
или

Докажем это свойство для средней взвешенной.

Имеем: варианты

частоты

откуда

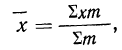
и

Подводя под общий знак суммы, получаем:

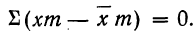
Следовательно,

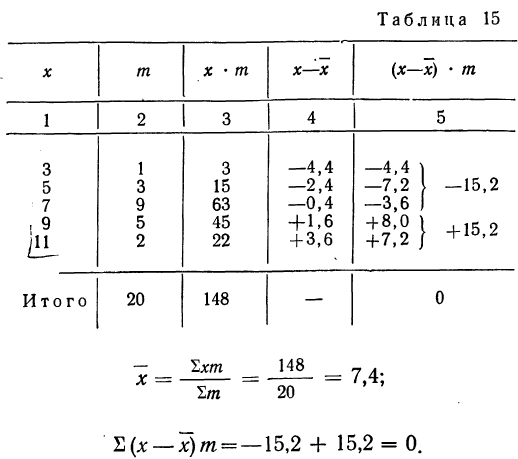
Пример 15.

Вычислить среднюю (по колонкам 1 и 2) и убедиться в правильности выведенной формулы.

3) Если у всех вариантов х частоты m равны друг другу, то средняя арифметическая взвешенная равна средней арифметической невзвешенной.

Имеем

4) Если из всех вариантов (х) вычесть постоянную величину и из результатов вычитания, т. е. из отклонений вариантов от этой постоянной величины вычислить среднюю то она окажется меньше искомой средней на эту постоянную величину Поэтому, чтобы получить среднюю из вариантов нужно к найденной средней прибавить ту же постоянную величину: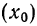

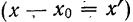
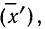
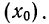
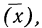
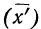
если

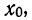
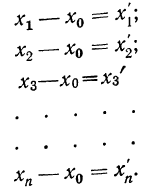
Имеем отклонения от постоянной величины обозначенные

Находим среднюю из

Откуда

Пример 16.

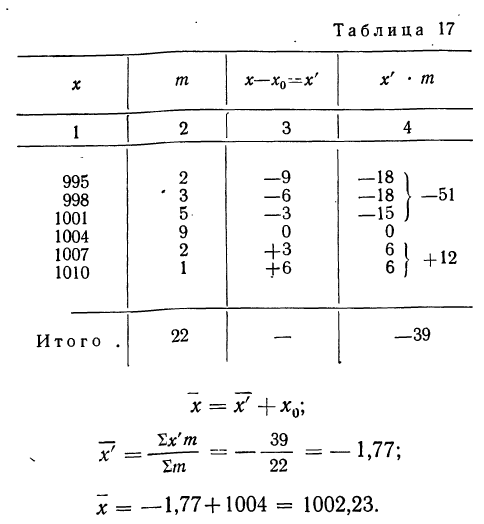
Вычислить среднюю путем вычитания 1000 из всех вариантов по следующим данным (колонки 1 и 2).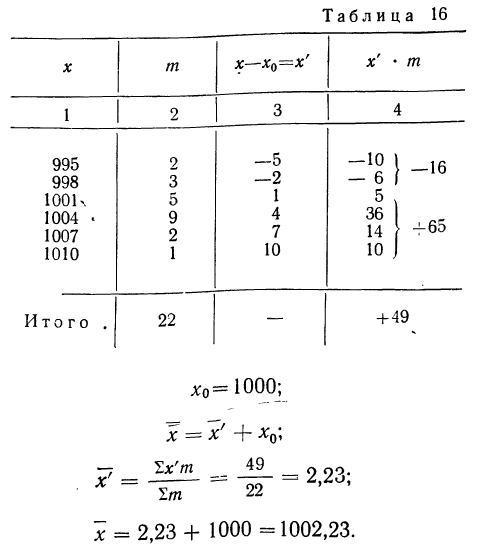
.

Пример 17.

Используя данные прёдыдущего примера, можно убедиться, что если за 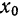взять не 1000, а 1004, то величина средней не изменится.

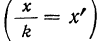
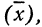
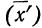
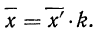
5) Если все варианты (х) уменьшить в одно и то же число раз, т. е. разделить на постоянную величину (k), и из частных вычислить среднюю, то онa окажется уменьшенной в такое же число раз, а поэтому, чтобы получить среднюю из вариантов нужно найденную среднюю умножить на ту же постоянную величину (k):

Доказательство.

Имеем частные от деления вариантов х на постоянную величину k, обозначенные х’:

Находим среднюю из

откуда

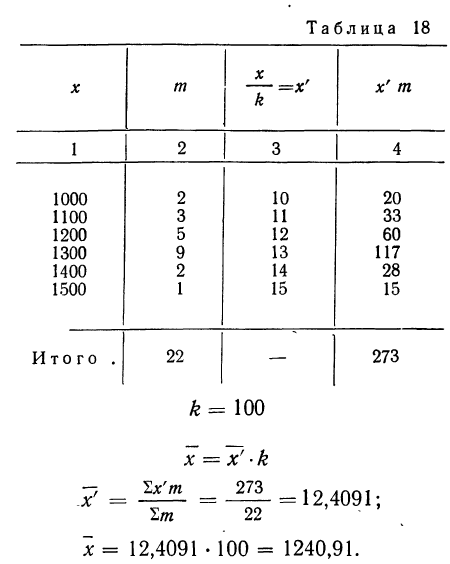
Пример 18.

Вычислить среднюю путем деления всех вариантов на 100 по следующим данным (колонки 1 и 2):

6) При вычислении средней вместо абсолютных значений весов (m) можно использовать относительные величины структуры (частости), т. е. удельные веса отдельных частот в общей сумме всех частот (см. § 4), или относительные величины координации, которые получаются путем отношения частот всех вариантов к одной из частот, принятой за единицу

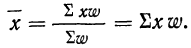
Если же удельные веса частот выражены в процентах, то

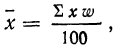
где 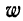— частость, т. е. доля частоты варианта в общей сумме частот.

Значит

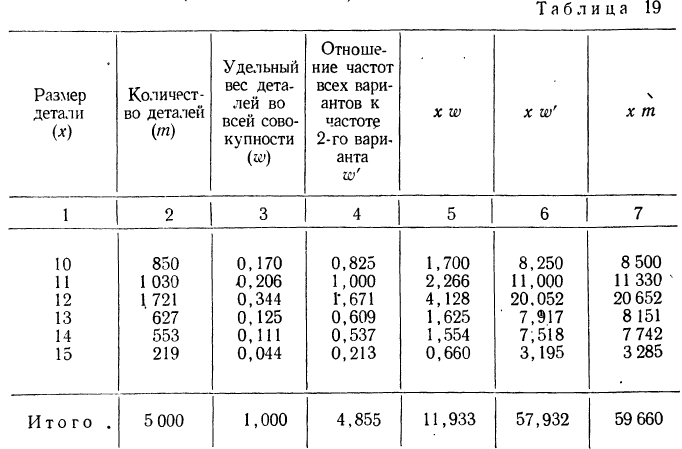
Пример 19.

Вычислить средний размер детали по следующим данным (колонки 1 и 2):

Предварительно найдем относительные величины структуры (колонка 3), а затем вычислим средний размер детали, используя их в качестве весов: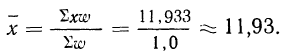

Если теперь вычислить средний размер детали, используя в качестве весов частоты, то получим: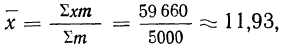

что согласуется с результатом, полученным ранее.

Для вычисления средней можно было использовать колонку 4 :

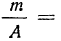
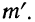
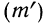
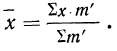
7) Если в частотах (m) имеется общий множитель (A), то его можно при вычислении средней не принимать во внимание т. е. взвешивание производить по сокращенным частотам Численное значение средней от замены частот (m) на сокращенные частоты не изменится

Доказательство.

Имеем:

Разделим частоты на общий множитель А, содержащийся в них:

Тогда

Пример 20.

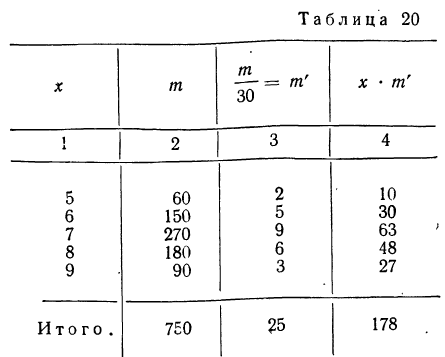
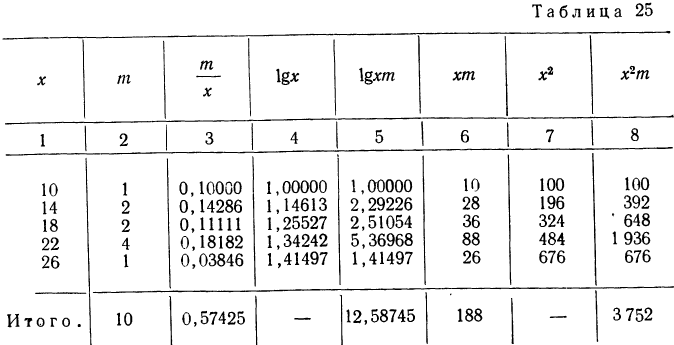
Вычислить среднюю по данным табл. 20 (колонки 1 и 2), произведя взвешивание вариантов по сокращенным весам.

Вычисляем среднюю по указанной формуле, предварительно сократив веса и заполнив колонки 3 и 4.

8) Общая средняя равна-.-взвешенной средней из частных средних: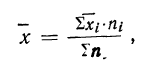

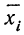
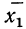
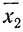
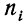
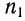
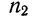
где — частные средние, т. е. средние для отдельных групп совокупности;

— средняя из вариантов первой группы;

— средняя из вариантов второй группы и т. д.;

— частоты отдельных групп;

— частота первой группы;

— частота второй группы и т. д.

Пусть имеются частные средние:

Найдем среднюю для всей совокупности:

Пример 21.

В трех, партиях продукции численностью 1000, 2000 и 500 единиц найден средний вес детали (в кг): 3,3; 3,1; 3,7. Вычислить средний вес детали во всех трех партиях

9) Сумма квадратов отклонений от средней меньше суммы квадратов отклонений от произвольной величины (В) на величину поправки С, равной произведению объема совокупности на квадрат разности между средней и данной произвольной величиной:

для случая невзвешенной средней или

для случая взвешенной средней.

Доказательство для случая невзвешенной средней.

Пользуясь свойствами сумм (см. стр. 11), производим преобразования:

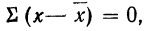
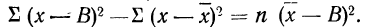
На основании второго свойства средней арифметической а поэтому

Пример 22.

По данным табл. 21 (колонки 1 и 2) убедиться в правильности указанных соотношений.

Вычисляем колонки 3, 4, 5, 6, 7, 8, 9 и находим:

Подставляя полученные результаты в формулу

имеем:

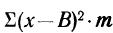
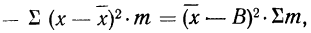
Метод отсчета от условного нуля

Упрощенное вычисление средней, состоящее в использовании ряда ее свойств, называется методом отсчета от условного нуля и предполагает:

Кроме того, в качестве весов используют сокращенные частоты 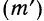или относительные величины (структуры или координации).

Формула исчисления средней методом отсчета от условного нуля:

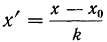
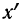
где , т. е. отклонение от начала отсчета делится на общий множитель, а исчисление средней из в зависимости от того, какими весами мы располагаем, производится по одной из следующих формул:

где 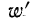— относительные величины координации (см. табл. 19).

Пример 23.

Вычислить средний вес зерен (на 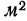) по данным колонок 1 и 2 табл. 22 (см. стр. 38), используя метод отсчета от условного нуля.

Используем формулу 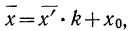предварительно заполнив колонки 3, 4, 5 и 6 табл. 22:

Метод стандартизации средних

Метод стандартизации средних наиболее разработан в статистике населения (демографической) и медицинской статистике, когда производится сравнение совокупностей с различными Структурами. Стандартизация достигается элиминированием (устранением) влияния различия в структурах совокупностей. Результат сравнения характеризует различие в средних при условии, что структура сравниваемых совокупностей одинакова.

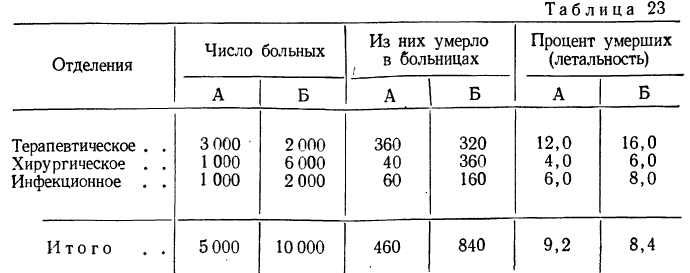
Рассмотрим применение метода стандартизации на примере из медицинской статистики. Имеются данные о двух больницах А и Б по отделениям и в целом.

Получается парадоксальное положение, при котором по больнице Б итоговая (общая) летальность (8,4%) ниже, чем в больнице А (9,2%), хотя по всем отделениям летальность в больнице Б выше (см. последние две колонки).

Причиной этого парадокса является отличие удельных весов разных отделений в больницах. Доля терапевтического отделения (по числу больных) с самой высокой летальностью составляет в больнице А 60%„ а в больнице Б — 20%, а доля хирургического отделения, с самой низкой летальностью, в больнице А — 20%, а в больнице Б — 60%.

Устраним влияние различия в структурах и стандартизуем распределение больных по отделениям. В качестве стандарта можно взять распределение больных по отделениям в любой больнице или привлечь данные о распределении больных нескольких других больниц. Возьмем за стандарт распределение больных в больнице А. Тогда по больнице А общая летальность (9,2%) останется без изменения. По больнице Б произведем пересчет.

Находим среднюю стандартизованную летальность больных больницы Б:

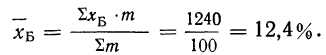
Таким образом, после стандартизации летальность в больнице Б оказалась значительно выше,, чем в больнице А: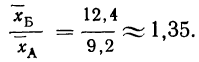

Следует иметь в виду, что полученное значение стандартизованной средней может служить только для сравнительных целей, абсолютное же ее значение принимать во внимание не следует.

Если за стандарт принять распределение больных в больнице Б, то получим следующую стандартизованную летальность для больницы А:

а отношение стандартизованных средних почти не изменится:

Мажорантность средних

Если вычислить различные типы средних для одного и того же вариационного ряда, то численные их значения будут отличаться друг от друга. При этом средние по своей величине расположатся в определенном порядке. Наименьшей из перечисленных средних окажется средняя гармоническая, затем геометрическая и т. д., наибольшей — средняя квадратическая. Порядок возрастания средних при этом определяется показателем степени z в формуле степенной средней и вытекает из «правила мажорантности».

Так,
при z= —1 получаем среднюю гармоническую,

при z= 0 »» геометрическую,

при z= 1 »» арифметическую,

при z= 2 »» квадратическую:

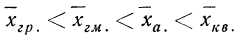
Подробное выяснение общего условия мажорантности впервые было произведено А. Я. Боярским, доказавшим, что если две средние должны удовлетворять соответственно уравнениям

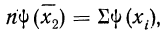
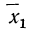
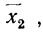
то первая из них мажорантна в отношении если при любом значении аргумента

Для степенной средней порядка z имеем: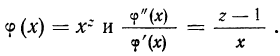

Это отношение для положительных значений с показателем x растет вместе с показателем z.

Пример 24.

Вычислить различные типы средних,по следующим данным (колонки 1 и 2) и убедиться в правильности порядка возрастания средних:

Заполняем колонки с 3-й по 8-ю и по соответствующим формулам исчисляем средние взвешенные:

Порядок средних определился в соответствии с правилом мажорантности:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник