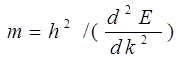Понятие об эффективной массе

При изучении поведения электронов в поле кристаллической решетки вводят понятие эффективной массы, выражаемой

Введение эффективной массы позволяет, пренебрегать взаимодействием электронов с решеткой, определять характер движения электрона под действием внешнего поля. В реальности, эффективная масса электрона никакого отношения к массе свободного электрона не имеет. Она является характеристикой системы электронов в кристалле в целом. Вводя понятие эффективной массы, реальному электрону в кристалле, связанному взаимодействиями с кристаллической решеткой и другими электронами, сопоставляют некую новую свободную “микрочастицу”, обладающую лишь двумя физическими параметрами реального электрона- его зарядом и спином. Все остальные параметры-квазиимпульс, эффективная масса, кинетическая энергии и т.д.- определяются свойствами кристаллической решетки. Такую частицу часто называют квазиэлетроном, электроном-квазичастицей, носителем отрицательного заряда или носителем заряда n-типа, чтобы подчеркнуть ее отличие от реального электрона.

Эффективная масса может быть как положительной, так и отрицательной. При положительной m электроны ведут себя во внешнем электрическом поле подобно свободным электронам: они ускоряются под действием внешнего электрического поля. Отличие таких электронов от свободных состоит лишь в том, что их эффективная масса может существенно отличаться от массы свободного электрона.

Для электронов, находящихся у вершины энергетической зоны, эффективная масса является величиной отрицательной. Такое поведение эффективной массы электрона объясняется тем, что он при своем движении в кристалле обладает не только кинетической энергией поступательного движения, но и потенциальной энергией его взаимодействия с кристаллической решеткой.

Источник

Содержание

Простой случай: параболическое, изотропное дисперсионное соотношение

E ( k ) = E 0 + ℏ 2 k 2 2 м ∗ < Displaystyle E ( mathbf ) = E_ <0>+ < frac < hbar ^ <2>mathbf ^ <2>> <2m ^ <*>>>>

Можно показать, что электроны, помещенные в эти зоны, ведут себя как свободные электроны, за исключением другой массы, до тех пор, пока их энергия остается в пределах применимости приведенного выше приближения. В результате масса электрона в таких моделях, как Модель Друде необходимо заменить на эффективную массу.

Одно замечательное свойство состоит в том, что эффективная масса может стать отрицательный, когда полоса изгибается вниз от максимума. В результате отрицательная массаэлектроны реагируют на электрические и магнитные силы, набирая скорость в противоположном направлении по сравнению с нормальным; хотя эти электроны имеют отрицательный заряд, они движутся по траекториям, как если бы они имели положительный заряд (и положительную массу). Это объясняет существование дыры валентной зоны, положительный заряд, положительная масса квазичастицы которые можно найти в полупроводниках. [1]

В любом случае, если ленточная структура имеет описанную выше простую параболическую форму, то значение эффективной массы однозначно. К сожалению, эта параболическая форма не подходит для описания большинства материалов. В таких сложных материалах нет единого определения «эффективной массы», а есть несколько определений, каждое из которых подходит для определенной цели. В остальной части статьи эти эффективные массы описаны подробно.

Промежуточный случай: параболическое, анизотропное дисперсионное соотношение.

В некоторых важных полупроводниках (в частности, в кремнии) зоны проводимости с самыми низкими энергиями несимметричны, так как поверхности с постоянной энергией теперь эллипсоиды, а не сферы в изотропном случае. Каждый минимум зоны проводимости можно аппроксимировать только

В этом случае движение электрона уже нельзя напрямую сравнивать со свободным электроном; скорость электрона будет зависеть от его направления, и он будет ускоряться в разной степени в зависимости от направления силы. Тем не менее, в кристаллах, таких как кремний, общие свойства, такие как проводимость, кажутся изотропными. Это потому, что есть несколько долины (минимумы зоны проводимости), каждый с эффективными массами, переставленными по разным осям. Долины вместе действуют вместе, обеспечивая изотропную проводимость. Можно каким-то образом усреднить эффективные массы различных осей вместе, чтобы восстановить картину свободных электронов. Однако оказывается, что метод усреднения зависит от цели: [4]

(Эта эффективная масса соответствует эффективной массе плотности состояний, описанной ниже.)

Общий случай

Тензор инерционной эффективной массы

где час = час/ 2π это приведенная постоянная Планка. Объединение этих двух уравнений дает

Извлечение я й элемент с обеих сторон дает

Обычно используется инерционное выражение для эффективной массы, но обратите внимание, что его свойства могут быть нелогичными:

Эффективная масса циклотрона

Классически заряженная частица в магнитном поле движется по спирали вдоль оси магнитного поля. Период Т его движения зависит от его массы м и зарядить е,

Для частиц в асимметричных ленточных структурах частица больше не движется точно по спирали, однако ее движение поперек магнитного поля все еще движется по замкнутому контуру (не обязательно по кругу). Более того, время завершения одной из этих петель по-прежнему изменяется обратно пропорционально магнитному полю, поэтому можно определить циклотронная эффективная масса от измеренного периода, используя приведенное выше уравнение.

Обычно эксперименты по измерению циклотронного движения (циклотронный резонанс, эффект де Хааса – ван Альфенаи т. д.) ограничиваются только движением зонда для энергий около Уровень Ферми.

Эффективные массы плотности состояний (слаболегированные полупроводники)

Эффективная масса плотности состояний в различных полупроводниках [6] [7] [8] [9]

Группа	Материал	Электрон	Дыра
IV	Si (4 K)	1.06	0.59
	Si (300 K)	1.09	1.15
	Ge	0.55	0.37
III-V	GaAs	0.067	0.45
	InSb	0.013	0.6
II-VI	ZnO	0.29	1.21
	ZnSe	0.17	1.44

В полупроводниках с низким уровнем легирования концентрация электронов в зоне проводимости обычно определяется выражением

В полупроводниках с непростой зонной структурой это соотношение используется для определения эффективной массы, известной как плотность состояний эффективная масса электронов. Название «эффективная масса плотности состояний» используется, поскольку приведенное выше выражение для N_C выводится через плотность состояний для параболической ленты.

На практике эффективная масса, извлеченная таким образом, не совсем постоянна по температуре ( N_C точно не меняется как Т 3/2 ). В кремнии, например, эта эффективная масса изменяется на несколько процентов между абсолютным нулем и комнатной температурой, потому что сама зонная структура немного меняет форму. Эти искажения зонной структуры являются результатом изменения энергий электрон-фононного взаимодействия, при этом тепловое расширение решетки играет незначительную роль. [6]

Точно так же количество дырок в валентной зоне и плотность состояний эффективная масса дырок определяются:

определение

Экспериментальный

Теоретическая

Разнообразие теоретических методов, включая теория функционала плотности, k · p теория возмущений, и другие используются для дополнения и поддержки различных экспериментальных измерений, описанных в предыдущем разделе, включая интерпретацию, подгонку и экстраполяцию этих измерений. Некоторые из этих теоретических методов можно также использовать для ab initio предсказания эффективной массы при отсутствии каких-либо экспериментальных данных, например, для изучения материалов, которые еще не были созданы в лаборатории.

Значение

Эффективная масса используется в транспортных расчетах, таких как перенос электронов под действием полей или градиентов носителей, но она также используется для расчета плотности носителей и плотность состояний в полупроводниках. Эти массы связаны, но, как объяснялось в предыдущих разделах, не одинаковы, потому что веса разных направлений и волновых векторов различны. Эти различия важны, например, в термоэлектрические материалы, где высокая проводимость, обычно связанная с малой массой, желательна одновременно с высокой Коэффициент Зеебека, обычно ассоциируется с большой массой. В этом контексте были разработаны методы оценки электронной структуры различных материалов. [12]

В апреле 2017 года исследователи из Университета штата Вашингтон заявили, что создали жидкость с отрицательной эффективной массой внутри Конденсат Бозе – Эйнштейна, разработав соотношение дисперсии. [14]

Источник

Эффективная масса электрона. Собственные и примесные полупроводники

Понятие эффективной массы электрона. Экспериментальное определение эффективной массы носителей. Зависимость энергии частицы от импульса, взаимосвязь эффективной массы и подвижности электронов. Основные внешние факторы, влияющие на электропроводность.

Рубрика	Физика и энергетика
Вид	реферат
Язык	русский
Дата добавления	27.04.2009
Размер файла	224,0 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

имени академика М.Ф. Решетнева

Кафедра технической физики

Реферат по курсу: Твердотельная электроника

Эффективная масса электрона. Собственные и примесные полупроводники

Красноярск 2008

Содержание

1. Понятие эффективной массы электрона

2. Эффективная масса и подвижность носителей

3. Расчет электропроводности полупроводниковых кристаллов на основе рассмотренных моделей

Библиографический список

1. Понятие эффективной массы электрона

Для свободной частицы закон дисперсии квадратичен, и таким образом эффективная масса является постоянной и равной массе покоя. В кристалле ситуация более сложна и закон дисперсии отличается от квадратичного. В этом случае только в экстремумах кривой закона дисперсии, там, где можно аппроксимировать параболой можно использовать понятие массы.

Эффективная масса зависит от направления в кристалле и является в общем случае тензором.

По определению эффективную массу находят из закона дисперсии :

где— волновой вектор,— символ Кронекера,— постоянная Планка.

Таб. 1. Эффективная масса для некоторых полупроводников

Эффективная масса электронов

Эффективная масса дырок

Эффективные массы могут также быть оценены, используя коэффициент и г из линейного слагаемого в низкотемпературного электронного вклада в теплоёмкость металла при постоянном объёме c_v. Теплоёмкость зависит от эффективной массы через плотность состояний на уровне Ферми.

Как показывает таблица, бинарные соединения III—V, основанные на GaAs и InSb имеют намного меньшие эффективные массы, чем материалы из четвёртой группы периодической системы, такие как кремний и германий. В самой простой картине электронного транспорта Друде, дрейфовая скорость носителей обратно пропорциональна эффективной массе:

2. Эффективная масса и подвижность носителей

Электрический ток в образце зависит не только от концентрации носителей заряда, но и от скорости с которой они переносятся под действием электрического поля. После того как мы научились рассчитывать концентрацию свободных носителей в твердом теле рассмотрим как ведут себя носители заряда в кристалле при наложении на него электрического поля.

Рассмотрение начнем с поведения единичного свободного заряда в нейтральной не взаимодействующей с зарядом среде (допустим в вакууме) при наличии электрического поля E, которое накладывается на среду в момент t=0. Электрическое поле приводит к возникновению силы электростатического взаимодействия F, под действием которой электрон начнет ускоряться.

Поскольку приобретаемая заряженной частицей энергия не зависит от направления электрического поля зависимость симметрична относительно импульса и волнового вектора (это параболоид выпуклость которого определяется массой частицы).

Измерив зависимость энергии частицы от импульса (или волнового числа), мы можем определить эффективную массу. Действительно, дважды продифференцировав вышестоящее уравнение получим.

Предположим, что на частицу действует некоторая тормозящая сила F* о существовании которой мы не знаем. Тогда уравнение можно переписать в следующем виде:

Соответственно, если для определения массы электрона (или любой другой заряженной частицы) в некоторой взаимодействующей с частицей среде воспользуемся формулой, то вместо массы электрона будет рассчитана некоторая другая величина, которую будем назвать эффективной массой электрона в данной среде.

Поскольку при движении электронов (или других заряженных частиц) в твердом теле внутренние поля неизвестны, то их характеристики используют понятие эффективной массы.

Рис. 1. Изменение скорости заряженной частицы в электрическом поле, при отсутствии взаимодействия со средой(1) и при торможении частицы средой

На рис. 1 показано как будет со временем изменяться скорость свободной частицы в электрическом поле, в соответствии формулами. Эти формулы справедливы для случая, когда заряженная частица не испытывает столкновений и в соответствии с ними частицу можно разогнать электрическим полем до бесконечной энергии. Именно этот принцип был использован в первых линейных ускорителях элементарных частиц.

По мере разгона частицы возрастает ее импульс и соответствующее ему волновое число (величина, характеризующая величину волнового вектора). На рис. 1.6. показаны соответствующие зависимости изменения энергии частицы от величины волнового числа (импульса).

Рис. 2. Зависимости энергии свободных зарядов от величины их волнового числа (импульса).

Как видно из рис. 1. и рис. 2 набираемая в электрическом поле энергия частицы зависит от скорости частицы (волнового числа) и массы. Поскольку выпуклость кривой характеризуется ее второй производной можно сделать вывод, что чем меньше эффективная масса частицы, тем больше выпуклость.

В кристалле энергия электрона (дырки) в разрешенной зоне не может превысить значение потолка разрешенной зоны, следовательно, импульс и волновой вектор так же имеют ограничения, причем максимальное значение волнового числа должно быть кратно постоянной решетки. На рис. 1.20 показана рассчитанное изменение энергии электрона от величины волнового числа (значения) импульса для кубического кристалла.

Из рисунка видно, что в электронном представлении у потолка валентной зоны знак эффективной массы изменяется (должно происходить отражение частицы). Следует отметить, что у дна зоны проводимости энергия имеет параболическую зависимость от импульса (волнового числа):

Если вести отсчет от дна зоны проводимости E_c = 0, то зависимость энергии электрона от импульса (волнового вектора) будет такая же как для свободного электрона см. (1.26). Это дает нам основание рассматривать электроны в зоне проводимости, находящиеся вблизи дна зоны проводимости как свободные частицы (иногда говорят квазисвободные или квазичастицы), считая, что они подчиняются тем же закономерностям, что и свободные частицы, но отличаются от них величиной эффективной массы, которую вблизи дна зоны можно считать постоянной (пока выполняется параболическое приближение).

Аналогичный подход справедлив и для дырки. Вводя дырку мы переходим от электронного представления к дырочному, т.е. мы принимаем, то масса дырки положительная, а заряд отрицательный и энергия ее отсчитывается от потолка валентной зоны к ее дну, тогда дырка будет вести себя так же как электрон у потолка валентной зоны. При этом энергия дырки у потолка валентной зоны так же изменяется по параболическому закону как и для электрона:

Таким образом, дырку, находящуюся потолка валентной зоны так же можно рассматривать как свободную частицу.

В реальной жизни электрон в электрическом поле не может набирать энергию до бесконечности, рано или поздно он столкнется с другой частицей и отдаст ей накопленную энергию. Вероятность столкновений частиц в газах и твердых телах характеризуется временем или длиной их свободного пробега. Эти же величины характеризуют движение носителей заряда в твердом теле.

Схема, приведенная на рис. 1 показывает изменение скорости электрона в образце, к которому приложено напряжение и поясняет физический смысл подвижности. Электрон участвует в хаотическом тепловом движении, причем в различные моменты времени его скорость имеет случайное направление так что смещение его в любом направлении равновероятно. В электрическом поле электрон приобретает дополнительную скорость под действием поля, так что продолжая участвовать в тепловом движении он постепенно смещается под действием поля. Средняя скорость тем выше, чем больше длина свободного пробега и чем меньше эффективная масса частицы.

Рис. 4. Диаграмма, поясняющая движение электрона в твердом теле

Поскольку электрон набирает энергию в поле за время свободного пробега и отдает ее при столкновении с решеткой или другими носителями заряда, то средняя скорость, которую приобретают носители в направлении поля, будем называть ее скоростью дрейфа зарядов v_др должна зависеть от средней длины свободного пробега ф.

Коэффициент пропорциональности между дрейфовой скоростью и напряженностью электрического поля обычно называют подвижностью носителей заряда и обозначают м:

Для единичной площади получится уравнение для плотности тока:

Поскольку в дифференциальной форме закон Ома имеет вид:

Сравнив предыдущиеформулы получим формулу для электропроводности:

таким борзом мы видим, что проводимость материала определяется двумя основными параметрами: подвижностью носителей заряда и их концентрацией.

Величина подвижности пропорциональна длине свободного пробега, которая зависит от частоты столкновений носителей заряда с решеткой или атомами примеси. Поскольку при столкновениях носители отдают энергию, а затем вновь набирают, т.е. энергия носителя релаксирует, то принято говорить о механизмах ее релаксации. За время релаксации принимают среднее время в течение которого электрон полностью отдает свою энергию.

Существует множество механизмов рассеяния (релаксации) энергии свободных носителей заряда. Однако, для полупроводников, наиболее существенные два: рассеяние на решетки и рассеяние на ионизованной примеси.

Для рассеяния на решетке справедливо:

Таким образом рост, в случае если доминирует рассеяние на решетке (примесей мало), то с ростом температуры подвижность падает и следовательно падает проводимость ( как это имеет место в металлах).

При рассеянии на заряженной примеси м_i

Таким образом, если в образце доминирует рассеяние на примесях, то с ростом температуры подвижность возрастает и соответственно возрастает проводимость.

Значения множителей м_r0 и м_i0 зависят от химического состава материала, наличия в нем дефектов и примесей, степени их ионизации (для разных образцов одного материала эти значения могут быть различными).

Характер изменения электропроводности полупроводников с температурой, в том случае, если не изменяется концентрация носителей заряда будет определяться температурной зависимостью подвижности и зависимости будут аналогичны показанным на рис. 2 (это может быть в примесной области температурной зависимости проводимости).

Рис. 5. Диаграмма, поясняющая температурную зависимость подвижности м_ef, при рассеянии на решетке м_r и ионизированной примеси м_iK.

3. Расчет электропроводности полупроводниковых кристаллов на основе рассмотренных моделей.

Электропроводность полупроводникового кристалла определяется электропроводностью электронов и дырок, поэтому для нее, используя полученные формулы, можно записать:

Как видно из электропроводность полупроводника зависит от концентрации носителей заряда и подвижности, значения которых зависят как от технологии так и температуры.

Для чистого бездефектного кристалла с проводимостью близкой к собственной справедливо n = p = n_i см. (1.19), тогда для электропроводности собственного полупроводника можно записать:

Поскольку у₀(T) слабо зависит от температуры в оценочных расчетах принимают предэкспонциальный множитель постоянным равным значению электропроводности при T>?. Формула хорошо описывает экспериментальную кривую электропроводности для чистых кристаллов с совершенной структурой (см. рис. 1. ) и из экспериментальной зависимости используя соотношение можно определить такие характеристические параметры материала как Eg и у₀.

Для легированного кристалла можно выделить несколько температурных областей как для изменения с температурой концентрации (см. п.п. 1.2.4 рис. 1.16 ), так и для изменения с температурой подвижности носителей заряда (см рис. 1). При этом в области, где доминирует примесная приводимость n_i(T) >n_пр полупроводник ведет себя как собственный (область I). В области низких температур (область III), там, где примесь не ионизована, уровень Ферми должен находиться выше донорного уровня (вероятность заполнения электронами больше 1/2). По мере того, как температура повышается, доноры отдают электроны в зону проводимости и постепенно полностью ионизуются (область II). Область II принято называть областью истощения примеси, поскольку все атомы доноров отдали свои электроны, а концентрация собственных электронов все еще очень мала, концентрация электронов в этой области остается постоянной и примерно равной концентрации примесных атомов. Именно эта температурная область и является основной областью работы значительной части полупроводниковых диодов и поскольку в области II концентрация носителей изменяется незначительно, то в электропроводности (кривая В) становится заметен вклад подвижности, что приводит к некоторому падению электропроводности с ростом температуры (что, вообще говоря, не характерно для полупроводников) в некотором интервале температур за счет доминирования рассеяния на колебаниях решетки. Затем с повышением температуры имеет место переход к собственной проводимости, концентрация электронов и электропроводность начинают возрастать экспоненциально с температурой.

Подводя итоги, можем сделать вывод, что в соответствии с рассмотренной моделью основными внешними факторами, влияющими на электропроводность, в рамках рассмотренных моделей являются: ширина запрещенной зоны, концентрация и тип примесей, глубина залегания примесных уровней.

В табл. 2 приведены параметры характеризующие кристаллы основных полупроводников с собственной проводимостью. В этой таблице так же приведены такие, параметры как работа выхода (расстояние от уровня Ферми в собственном полупроводнике до нулевого уровня в вакууме) и сродство к электрону расстояние от уровня Ферми в собственном полупроводнике до нулевого уровня в вакууме)

Таб.2. Параметры полупроводниковых материалов

Источник

Эффективная масса что такое

Вспомним, как вводился матричный элемент оператора импульса в форме

+ .

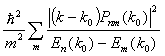
Если точка k₀ экстремальная, то линейный член по P_nm(k₀) исчезает, и закон дисперсии будет определяться квадратом матричного элемента оператора импульса:

E_n(k) = E_n(k₀) + 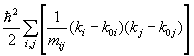, (i, j = x, y, z),

где под m_ij понимается эффективная масса, определяемая выражением

= + .

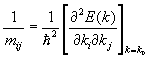
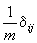
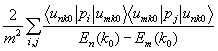
Понятие тензора эффективной массы, о котором говорилось с самого начала, когда вводились первые понятия о законе дисперсии, широко используется, так как компоненты тензора можно измерить в эксперименте по циклотронному резонансу. Матрица эффективной массы поддается диагонализации, что позволяет найти три собственных значения m_x, m_y, m_z. Тогда закон дисперсии вблизи экстремума запишется как

E_n(k) – E_n(k₀) = + + .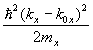

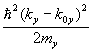
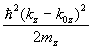
Часто два из трех компонентов эффективной массы одинаковые, и тогда говорят о продольной и поперечной массе. Физический смысл эффективной массы состоит в том, что направление ускорения электрона ( dv/dt ) под действием кристаллического поля V(r) не совпадает с направлением силы ( F ). Если в изотропном пространстве движение электрона описывается уравнением

или ,

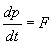
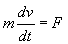
то в анизотропном пространстве кристалла масса зависит от направления движения (рис. 49):

.

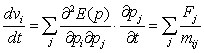
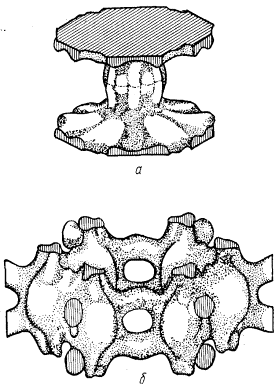
Физический смысл квадратичной зависимости закона дисперсии тоже понятен: в экстремальных точках энергетические уровни можно аппроксимировать параболами, вдали от этих точек линии уровней спрямляются и их можно аппроксимировать прямыми или, если речь идет о k-пространстве, плоскостями. При поиске параметров импульса возникает потребность опереться на какую-то, пусть грубую, модель всех энергетических уровней в целом. Эту модель не может дать зонная структура пустой решетки (рис. 44а), поскольку вблизи запрещенной зоны кристаллический потенциал слишком сильно искривляет общую картину энергетических состояний (см. рис. 44б). Значит, требуется более адекватная пространственная модель уровней, дающая наглядное представление о расположении энергетических зон. Такая модель может быть получена за счет линейной аппроксимации закона дисперсии, когда ее квадратичный компонент опускается, а линейный удерживается:

Этот линейный закон описывает положение плоскостей в четырехмерном пространстве энергии и волнового вектора (E, k_x, k_y, k_z). В следующем пункте ставится задача получения числовых значений коэффициентов уравнений плоскости для уровней германия и кремния. Но прежде, чем мы приступим к решению этой линейной задачи, необходимо рассмотреть вопрос с противоположной стороны, а именно: как выглядят максимально искривленные поверхности вблизи точек экстремума.

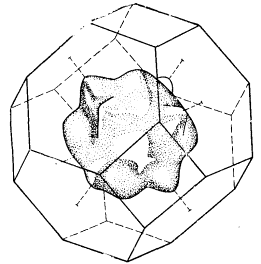
Закон дисперсии E_n(k) — функция четырехмерного пространства; чтобы ее отобразить в трехмерном k-пространстве, требуется прибегнуть к небольшой хитрости. Первый способ состоит в том, чтобы выбрать определенное направление в k-пространстве и вдоль него вычертить значения энергии (этим способом мы до сих пор пользовались). Второй способ состоит в том, чтобы вычертить в трехмерном объеме k-пространства одну-единственную энергетическую поверхность постоянного значения. Возникает вопрос: какую поверхность постоянной энергии нужно вычертить, чтобы она наиболее полно характеризовала изучаемый материал? Здесь и появляется понятие о поверхности Ферми, которое потребует от нас некоторых разъяснений.

Число значений волнового вектора k внутри зоны Бриэллюэна (ЗБ) равно числу элементарных ячеек в кристалле, которое мы обозначим N. Так как в каждом состоянии могут находиться два электрона с противоположными спинами, то число разрешенных состояний, приходящихся на одну энергетическую зону, равно 2N. Если полное число электронов проводимости, отдаваемых всеми атомами, находящимися в каждой элементарной ячейке кристалла, равно n, то полное число электронов проводимости, которые нужно разместить в различных возможных состояниях, характеризуемых величинами k и E_i(k), равно nN. Значит, эти электроны заполнят nN/2N = n/2 зон в ЗБ. Какие именно из 2N состояний будут заняты электронами, определяется законом распределения Ферми — Дирака. Вероятность того, что состояние с волновым вектором k в зоне E_i(k) при температуре Т будет занято, определяется формулой:

,

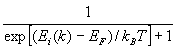
где E_F — энергия Ферми и k_B — постоянная Больцмана. При Т = 0 зоны E_i(k) E_F окажутся свободными; при температуре Т > 0 часть электронов перейдет в зону проводимости (ЗП), которая для проводников, где нет запрещенной зоны (ЗЗ), находится сразу же выше уровня Ферми. Таким образом, энергия E_F играет ключевую роль, особенно для металлов; поверхность постоянной энергии, определяемая уравнением E_i(k) = E_F и называется поверхностью Ферми. Для полупроводников понятие энергия Ферми существенно девальвирует: для этого класса материалов более важными энергиями являются величины, соответствующие потолку и дну ЗЗ. Поскольку в ЗЗ располагаются энергетические уровни примесей, то для сравнения этих уровней иногда оказывается полезно ориентироваться на Фреми-уровень, как некий порог, с которого начинается движение акцепторов и доноров в полупроводнике.

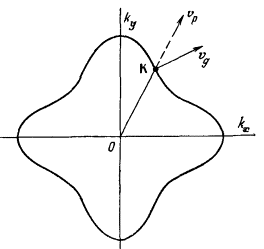
Ферми-поверхность может представлять собой сфероид, эллипсоид, односвязанную или многосвязанную поверхность. Причем эти поверхности не обязательно должны быть целиком замкнуты в первой ЗБ, поскольку они могут иметь продолжение в соседние ЗБ. Физические свойства материалов в значительной степени зависят от топологии поверхности Ферми. В общем виде кривизна зоны E_i(k) записывается

,

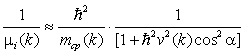
где m_ср — средняя эффективная масса, v(k) — скорость электрона, α — угол между направлениями групповой (v_g) и фазовой (v_p) скорости для деформированных изоэнергетических поверхностей (рис. 50). Более точное аналитическое выражение, связывающее эффективную массу с кривизной поверхности Ферми, выглядит более сложно.

Расчетная топология изоэнергетических поверхностей вообще и поверхность Ферми в частности существенно зависит от метода приближения, по которому ведется расчет. Предположим, что электрон в основном s-состоянии (для p, d и других состойний формулы будут сложнее) движется в поле V(r) изолированного атома. Тогда, как было сказано выше, волновая функция одного электрона в кристалле ψ_k(r) может быть записана в виде линейной комбинации атомных функций φ(r – r_j):

.

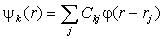
Функция ψ_k(r) является блоховской, а это значит, что коэффициенты в линейной комбинации имеют вид

Отсюда проистекает, что

.

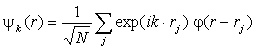
Энергия ищется как диагональный матричный элемент гамильтониана H:

;

.

и .

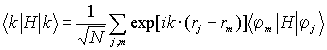
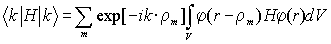
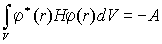
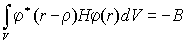
Знак минус говорит, что за счет сближения атомов, потенциальный барьер для туннелированния электрона от одного атома к другому снижается.

Таким образом, для энергии в первом приближении сильной связи имеем следующее выражение:

.

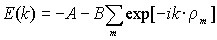
В ПК решетке с периодом а каждый атом окружен шестью соседями (±a, 0, 0), (0, ±a, 0), (0, 0, ±a). Если оси координат x, y, z направлены по ребрам куба, то сумма распишется как

= exp(ik_xa) + exp(–ik_xa) +

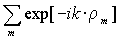
После преобразования суммы, закон дисперсии для ПК решетки приобретет вид

В ОЦК решетке число ближайших атомов равно 8 и закон дисперсии выглядит иначе

В ГЦК решетке число ближайших атомов равно 12 и закон дисперсии имеет вид

Для ПК решетки при условии k_x = k_y = k_z = 0,

Следовательно, ширина разрешенной энергетической зоны равна

Аналогичные рассуждения, проведенные для ОЦК решетки, дают

и такое же значение для ГЦК:

Вблизи дна ЗП энергия не зависит от направления движения и эффективная масса электрона будет равны

Отсюда видно, что при большом значении интеграла перекрытия соседних атомов (т.е. параметра B) разрешенная зона энергии для электрона (т.е. параметр ΔE) увеличивается, но его эффективная масса уменьшается и наоборот.

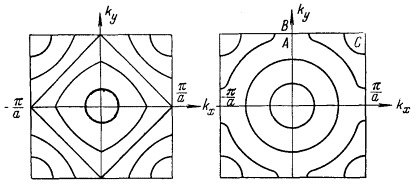
На рис. 51а приведены изоэнергетические уровни, рассчитанные по упрощенной методике, которая была продемонстрирована только что. Здесь энергии E = – A + 2B соответствуют прямые типа k_x + k_y = π/a, соединяющие середины ЗБ ПК решетка. На рис. 51б приведены изоэнергетические уровни, полученные в приближении слабой связи. Их сравнение показывает, что в центре и вблизи вершин квадрата ЗБ энергетические уровни схожи, но на осях k_x и k_y, а также в средней части ЗБ ПК решетки уровни сильно отличаются.

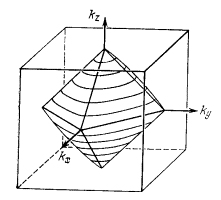
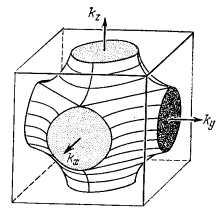
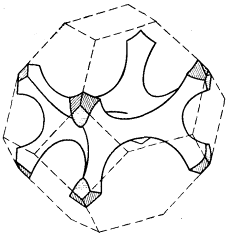
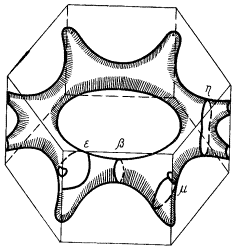
На рис. 52а показан изоэнергетический октаэдр ЗБ ПК решетки, отвечающий всё той же энергии E = –A + 2B; при другом значении энергии, а именно, при E = –A, поверхность становится криволинейной (рис. 52б). Внутренний объем обеих фигур, показанных на рис. 52а и 52б, заключают в себе электронные состояния. На рис. 52в показано дополнение к поверхности, которая изображена на рис. 52б; внутренний объем этой фигуры отделяет уже дырочные состояния.

а)

б)

в) .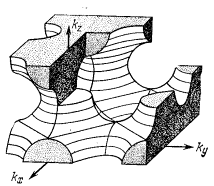

Изоэнергетические линии и поверхности, изображенные на рис. 51 и рис. 52, носят грубо-теоретический, качественный характер. В реальных полупроводниках дело обстоит намного сложнее. Впрочем, вблизи точки k = 0 всё-таки допустимо пользоваться приближенной формулой для закона дисперсии в виде

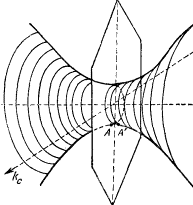
где A, B, C — экспериментальные параметры конкретных полупроводников. Два знака перед корнем дают две поверхности: минус для тяжелых дырок, плюс для легких.

Для Ge и Si имеют место следующие значения эффективной массы: m_l /m — продольная масса электронов; m_t/m — поперечная масса электронов; m_h1/m — эффективная масса тяжелых дырок; m_h2/m — эффективная масса легких дырок; m_h3/m — эффективная масса дырок отщепленной зоны. В табл. 40 приведены параметры в единицах ћ 2 /2m и эффективные массы в единицах массы свободного электрона m.

–A	| B |	| C |	ml /m	mt/m	mh1/m	mh2/m	mh3/m
Ge	13.3	8.6	12.5	1.64	0.082	0.28	0.044	0.077
Si	4.0	1.1	4.1	0.98	0.19	0.49	0.16	0.245

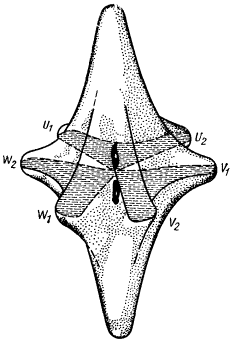
Три дырочных массы определяются трехкратно вырожденным состоянием Г ‘₂₅ валентной зоны. От него отходят две относительно крутые долины Δ‘₂ и Λ₁ (рис. 47) с малой кривизной вблизи точки k = 0, определяющие массу тяжелых дырок m_h1. От Г ‘₂₅ отходят также две пологие двукратно вырожденные долины Δ₅ и Λ₃, которые определяют массу легких дырок. В результате спин-орбитального взаимодействия двукратное вырождение слегка снимается, почему и возникают две разновидности легких дырок m_h2 и m_h3. Параметры закона дисперсии вблизи точки k = 0 связаны формулами:

, , .

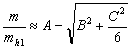
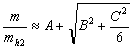
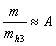
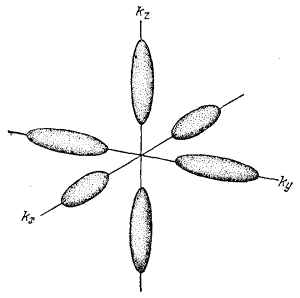
Минимум зоны проводимости у кремния находится в Δ-направлении ЗБ, т.е. на осях k_x, k_y, k_z. Отношение между продольной и поперечной массами электронов, равное m_l/m_t = 5, определит степень вытянутости шести эллипсоидов постоянной энергии (рис. 53). Минимум зоны проводимости у германия находится в Λ-направлении около точки L, а это означает, что изоэнергетическая поверхность вблизи минимума у него представляется восемью половинками эллипсоидов, обрезанных гексагональной гранью первой ЗБ. Отношение малой оси эллипсоида к большой равно 1 : 2.

.

В табл. 41 по материалам [47], [56], [57] приведены параметры A, B, C, эффективные массы электронов m_e, тяжелых m_hh и легких m_lh дырок. C увеличением ширины ЗЗ E_g (измеряется в эВ) эффективная масса электронов и легких дырок растет.

–A	| B |	| C |	me /m	mhh/m	mlh/m	Eg
InSb	26.5	24.1	13.9	0.015	0.4	0.016	0.23
InAs	17.1	14.9	10.9	0.024	0.41	0.026	0.36
GaSb	11.2	7.9	10.2	0.042	—	0.052	0.81
GaAs	7.39	4.93	5.06	0.065	0.68	0.07	1.52
GaP	4.72	2.52	2.70	0.135	—	—	2.3
InP	8.13	5.81	5.11	0.078	—	—	1.42
AlSb	5/51	2.84	3.65	0.121	—	—	1.6

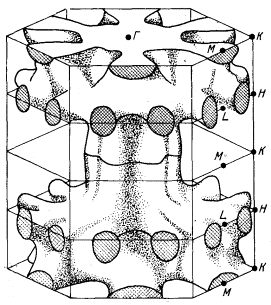
Далее приводятся рисунки ферми-поверхности для реальных металлов, взятые из работы [58].

Топология поверхности Ферми для меди, серебра и золота приблизительно одинаковая и представляет собой гофрированный сфероид, который через узкие трубки соединяется со сфероидами соседних ЗБ. На рис. 54а показан сфероид меди; на рис. 54б изображено соединение двух сфероидов в плоскости гексагональной грани, а на рис. 54в дана общая картина соединения нескольких ферми-сфероидов.

а)

б)

в) .

На рис. 55 показана многосвязанная ферми-поверхность дырочного типа для кальция (а), магния (б) и цинка (в)

а)

б)

в) .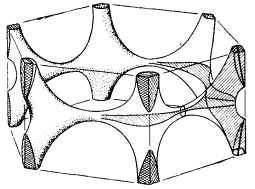

Электронная поверхность Ферми для родия и палладия схожи (рис. 56а), но их дырочные ферми-поверхности различаются: для родия она показана на рис. 56б, для палладия — на рис. 56в.

а)

б)

в) .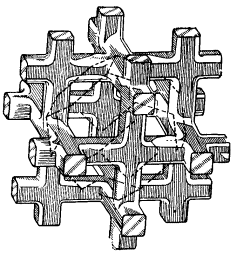

На рис. 57а показана электронная поверхность Ферми кадмия. Энергия Ферми в хроме, молибдене и вольфраме отвечает нескольким замкнутым электронным и дырочным поверхностям (рис. 57б). На рис. 57в изображена многосвязанная электронная поверхность Ферми β-латуни (CuZn), имеющая дырочные «карманы».

а)

б)

в) .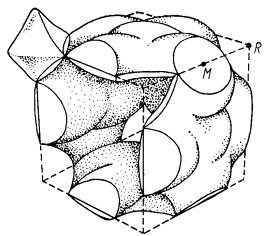

На рис. 58а представлена сложная многосвязанная ферми-поверхность скандия (электронная область заштрихована). На двух следующих рисунках приведены поверхности лантаноидов: б) тербия (вверху дырочная область, внизу электронная) и в) тулий (дырочная область заштрихована).

а)

б)

в) .

Источник