если плюс умножить на минус что получится
Почему минус на минус всегда даёт плюс?
Польза натуральных чисел
Для начала немного окунёмся в историю арифметики. Совершенно естественно, что в самом начале люди пользовались только натуральными числами — один, два, три и так далее. Их использовали для того, чтобы посчитать реальное количество предметов. Просто так, в отрыве от всего, цифры были бесполезны, поэтому стали появляться и действия, с помощью которых стало возможно оперировать числами. Абсолютно логично, что самым необходимым для человека стало сложение. Эта операция проста и естественна — подсчитать количество предметов становилось проще, теперь не нужно было каждый раз считать заново — «один, два, три». Заменить счёт теперь стало возможным с помощью действия «один плюс два равно три». Натуральные числа складывались, ответ тоже был натуральным числом.
Умножение представляло собой, по сути, такое же сложение. На практике мы и сейчас, например, совершая покупки, так же используем сложение и умножение, как это делали давным-давно наши предки. Однако порой приходилось совершать операции вычитания и деления. И числа не всегда были равнозначны — иногда число, от которого отнимали, было меньше числа, которое вычитали. То же и с делением. Таким образом и появились дробные числа.
Появление отрицательных чисел
В документах Индии записи об отрицательных числах появились в VII веке нашей эры. В китайских документах существуют более древние отметки об этом математическом «факте».
В жизни мы чаще всего отнимаем от большего числа меньшее. Например: у меня есть 100 рублей, хлеб и молоко стоят 65 рублей; 100 — 65 = 35 рублей сдачи. Если же я захочу купить ещё какой-то товар, стоимость которого превышает мои оставшиеся 35 рублей, например ещё одно молоко, то как бы я ни хотел его приобрести, а больше денег у меня нет, следовательно, отрицательные числа мне ни к чему.
Практически для таких же целей и начали впервые использовать отрицательные числа. Китайцы первыми использовали их для записи долгов или в промежуточных решениях уравнений. Но использование это было всё равно лишь для того, чтоб прийти к положительному числу (впрочем, как и наше погашение кредитки). Долгому отвержению отрицательных чисел способствовало то, что они не выражали конкретных предметов. Десять монет — это десять монет, вот они, их можно потрогать, на них можно купить товар. А что значит «минус десять монет»? Они предполагаются, даже если это долг. Неизвестно, вернётся ли этот долг, и превратятся ли «записанные» монеты в реальные. Если при решении какой-нибудь задачи получалось отрицательное число, считалось, что вышел неверный ответ или ответа вообще не существует. Такое недоверчивое отношение сохранялось у людей достаточно долго, даже Декарт (XVII век), совершивший прорыв в математике, считал отрицательные числа «ложными».
Формирование правил действий с отрицательными числами
Рассмотрим уравнение 9х-12=4х-2. Для решения уравнения нужно перенести члены с неизвестным в одну сторону, а известные числа — в другую. Это можно выполнить двумя способами.
Переносим часть уравнения с неизвестным в левую сторону, а другие числа — в правую. Получается:
Ответ найден. За все действия, что нам потребовалось выполнить, мы ни разу не прибегнули к использованию отрицательных чисел.
Теперь переносим часть уравнения с неизвестным в правую сторону, а остальные слагаемые — в левую. Получаем:
Чтобы найти решение, нам нужно одно отрицательное число разделить на другое. Однако верный ответ мы уже получили в предыдущем решении — это х, равное двум. Следовательно, остаётся вывести, что (-10)/(-5)=2.
Что доказывают нам эти два способа решения одного уравнения? Первое, что становится ясно – это то, каким образом выводилась адекватность оперирования отрицательными числами — полученный ответ должен быть таким же, что и при решении с использованием только натуральных чисел. Второй момент — это тот факт, что не нужно больше задумываться над величинами, чтобы получать непременно неотрицательное число. Можно выбирать наиболее удобный способ решения, особенно это касается сложных уравнений. Действия, которые позволили не задумываться над некоторыми операциями (что нужно сделать, чтоб были только натуральные числа; какое число больше, чтоб вычитать именно от него и т.д.), стали первыми шагами к «абстракцианизации» математики.
Естественно, не все правила действий с отрицательными числами сформировались единовременно. Копились решения, обобщались примеры, на основе чего и стали понемногу «вырисовывать» основные аксиомы. С развитием математики, с выделением новых правил, появлялись новые уровни абстракции. Например, в девятнадцатом веке стало доказано, что целые числа и многочлены имеют много общего, хотя внешне отличаются. Все их можно складывать, вычитать и перемножать. Правила, которым они подчиняются, влияют на них одним образом. Что же касается деления одних целых чисел на другие, то здесь «поджидает» занимательный факт — ответом не всегда будет целое число. Этот же закон распространяется и на многочлены.
Затем было выявлено множество других совокупностей математических объектов, над которыми возможно было производить такие операции: формальные степенные ряды, непрерывные функции. Со временем математики установили, что после исследования свойств операций результаты станет возможно применять ко всем этим совокупностям объектов. Точно так же работают и в современной математике.
Больше интересных материалов:
Сугубо математический подход
С течением времени математики выявили новый термин — кольцо. Под кольцом подразумевают множество элементов и операции, которые можно над ними производить. Основополагающими становятся правила (те самые аксиомы), которым подчиняются действия, а не природа элементов множества. Для того, чтоб выделить первостепенность структуры, возникающую после введения аксиом, как раз обычно и употребляют термин «кольцо»: кольцо целых чисел, кольцо многочленов и т. п. Используя аксиомы и исходя из них, можно выявлять новые свойства колец.
Сформулируем правила кольца, похожие на аксиомы операций с целыми числами, и докажем, что в любом кольце при умножении минуса на минус выходит плюс.
Под кольцом понимается множество с двумя бинарными операциями (в каждом действии участвуют два элемента кольца), традиционно именуемыми сложением и умножением, и следующими аксиомами:
— сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (—A)), что A + (—A) = 0;
— умножение подчиняется сочетательному закону: A · (B · C) = (A · B) · C;
— сложение и умножение связаны следующими правилами раскрытия скобок:
(A + B) · C = A · C + B · C
A · (B + C) = A · B + A · C.
Уточним, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (операция деления не всегда возможна), ни существования единицы — нейтрального элемента по умножению. Если ввести данные аксиомы, получим другие алгебраические структуры, однако со всеми действующими теоремами, доказанными для колец.
Из этого получим утверждения про единицы:
Далее следует доказать некоторые моменты. Во-первых, нужно установить существование лишь одной противоположности для каждого элемента. Допустим, наличие у элемента А два противоположных элемента: B и С. То есть A + B = 0 = A + C. Разберём сумму A + B + C. Используя переместительный и сочетательный законы, а также свойства нуля, получим, что сумма равна:
B: B = B + 0 = B + (A + C) = A + B + C
C: A + B + C = (A + B) + C = 0 + C = C.
Следовательно, B = C.
Отметим, что и A, и (-(-A)) противоположны к элементу (-A). Отсюда заключаем, что элементы A и (-(-A)) должны быть равны.
Далее, 0 = 0 · B = (A + (-A)) · B = A · B + (-A) · B,
Заметим, что 0 · B = 0 для любого элемента B.
0·B = (0 + 0) B = 0·B + 0·B,
таким образом, прибавление 0·B не изменяет сумму. Получается, это произведение равно нулю.
Как умножать отрицательные числа
Основные определения
Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.
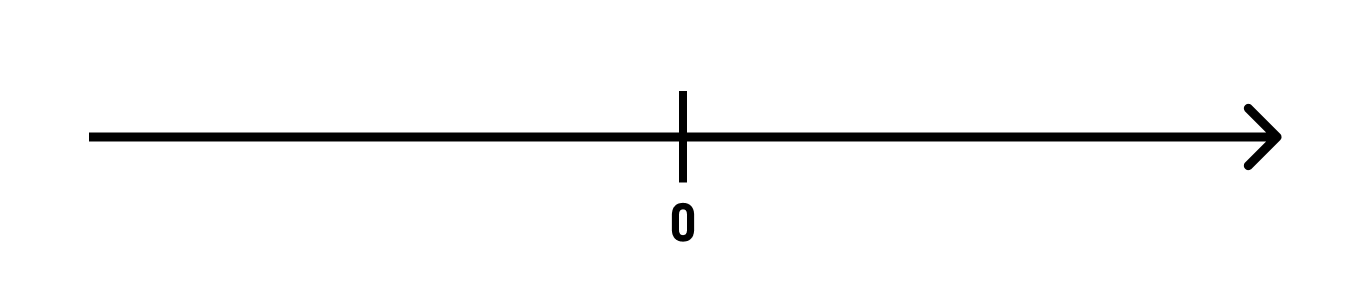
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:
Два главных определения:
Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.
Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».
Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!
Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).
Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.
Умножение отрицательных чисел
А вот как умножить два числа с разными знаками:
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
Примеры умножения отрицательных чисел
Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)
Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:
Пример 2. Вычислить: (-11)∗11 и (-20)∗2
Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:
Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)
Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:
Пример 4. Вычислить произведение: (-0,125 ) * (-6)
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
А давайте зададимся.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа.
Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3.
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции. Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами:
-сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (–A)), что A + (–A) = 0;
-умножение подчиняется сочетательному закону: A·(B·C) = (A·B)·C;
сложение и умножение связаны такими правилами раскрытия скобок: (A + B)·C = A·C + B·C и A·(B + C) = A·B + A·C.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1.
Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Значит, B = C.
Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны.
Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B).
Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Почему минус на минус дает плюс?
1) Почему минус один умножить на минус один равно плюс один?
2) Почему минус один умножить на плюс один равно минус один?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции. Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
умножение отрицательных
Умножить отрицательные в отличии от некоторых других действий с отрицательными, например сложение и вычитание существует только два варианта:
Об умножении отрицательных чисел.
Правила умножения отрицательных чисел.
Для умножения отрицательных чисел существует только два пункта в правилах «умножения отрицательных чисел» :
Первый пункт правил умножения звучит так : «если два множителя отрицательные, то при умножении минус на минус дает плюс, т.е. умножение двух отрицательных чисел равно умножению этих же чисел без минуса.»
1.2.) Если у множителей противоположные знаки.
Второй пункт правил умножения звучит так : «если из двух множителей только один отрицательный, то при умножении, минус на плюс, дает минус, т.е. у произведения знак будет отрицательным.»
Умножить отрицательные числа.
Пример умножения двух отрицательных чисел
У нас два отрицательных числа и мы их должны умножить :
У множителей два минуса, а как мы знаем из правил, минус на минус дает плюс. Значит, убираем у наших множителей два минуса.
(-12) * (-15) = 12 * 15 = 180
Умножить отрицательное и положительное число.
Рассмотрим пример умножения отрицательных чисел по второму пункту правил.
Для этого нам понадобятся цифры :
Как мы знаем из правил, в случае, если отрицательное число только одно, то результат умножения будет отрицательным:
Умножить отрицательные числа на калькуляторе.
Мы уже умножали два отрицательных числа, теперь сделаем умножение отрицательных чисел на калькуляторе!
Набираем первый множитель 12.
Набираем второй множитель : 15.
Меняем знак на отрицательный, кнопкой плюс/минус : «±».
Получаем результат умножения двух отрицательных чисел.
Умножить отрицательное и положительное число на калькуляторе.
Нам осталось разобрать умножение отрицательных на калькуляторе если одно из множителей отрицательное.
Набираем первый множитель 12.
Набираем второй множитель : 15.
Получаем результат умножения двух отрицательных чисел, где лишь один из множителей отрицательный.



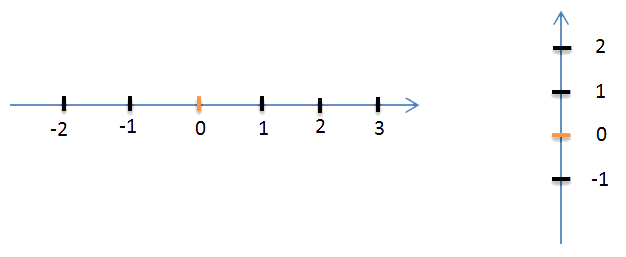
 masterok
masterok






