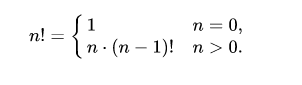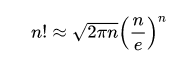Факториал 2020 чему равен
Факториал числа
Факториал числа — математическое понятие, которое означает произведение всех натуральных чисел от 1 до этого числа. Обозначается факториал просто — n!
Калькулятор факториалов
Рассмотрим понятие факториала более подробно. Факториал числа можно найти следующим образом. Допустим, что мы хотим найти факториал 7. Для этого нам необходимо перемножить все натуральные число от 1 до 7:
7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
Факториал 3 будет находится аналогично — 3! = 1 * 2 * 3 = 6.
Факториал 0
Существует особая договоренность — правило, по которому факториал нуля = 1. Т. е.
Это необходимо запомнить.
Таблица факториалов
Для удобства вычисления факториалов чисел от 0 до 10 можно использовать следующую таблицу. Если же вам необходимо рассчитать значение факториала числа, которое больше 10, то воспользуйтесь онлайн калькулятором, который находится выше на странице.
| Число | Факториал числа (n!) |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
Факториал широко применяется в комбинаторике и теории вероятностей для расчета числа сочетаний. Вы также можете познакомиться с двойным факториалом.
Калькулятор факториалов онлайн
Добро пожаловать на сайт Pocket Teacher
Наш искусственный интеллект решает сложные математические задания за секунды
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
начать
Факториалы
Что такое факториалы и как их решать
Факториал имеет математический смысл, только тогда, когда если это число целое и положительное (натуральное). Этот смысл следует из самого определения факториала, т.к. все натуральные числа неотрицательные и целые. Значения факториалов, а именно результат умножения последовательности от единицы до числа n можно посмотреть в таблице факториалов. Такая таблица возможна, по причине того, что значение факториала любого целого числа известно заранее и является, так сказать, табличным значением.
По определению 0! = 1. То есть если имеется ноль факториал, то мы ничего не перемножаем и результат будет первым натуральным существующим числом, то есть один.
Рост функции факториала можно отобразить на графике. Это будет дуга, похожая на функцию икса в квадрате, которая будет стремиться быстро вверх.
Факториал – является быстрорастущей функцией. Она растет по графику быстрее, чем функция многочлена любой степени и даже экспоненциальная функция. Факториал растет быстрее многочлена любой степени и экспоненциальной функции (но при этом медленнее двойной экспоненциальной функции). Именно поэтому, чтобы посчитать факториал вручную могут быть сложности, так как результатом может получиться очень большое число. Чтобы не считать факториал вручную, можно воспользоваться калькулятором подсчёта факториалов, с помощью которого вы можете быстро получить ответ. Факториал применяется в функциональном анализе, теории чисел и комбинаторике, в которой имеет большой математический смысл, связанный с числом всевозможных неупорядоченных комбинаций объектов (чисел).
Чтобы быстро рассчитать число комбинаций n чисел, нужно всего лишь посчитать n!. После подсчёта значения факториала калькулятором, искомое значение можно использовать в решении более сложных задач. Вы можете посмотреть необходимый факториал в таблице: «Таблица факториалов»
Бесплатный онлайн калькулятор факториалов
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Факториал
ЧТО ТАКОЕ ФАКТОРИАЛ
Для нахождения факториала нужно умножить все целые числа от выбранного нами числа до 1.
Факториал обозначается символом «!»
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1 = 120
Обычно говорят 4! как «факториал четырех».
ВЫЧИСЛЕНИЕ ФАКТОРИАЛА
Можно легко рассчитать факториал, зная значение факториала предыдущего числа:
Можно это записать в виде таблицы:
| n | n! | ||
| 1 | 1 | 1 | 1 |
| 2 | 2 x 1 | = 2 x 1! | = 2 |
| 3 | 3 x 2 x 1 | = 3 x 2! | = 6 |
| 4 | 4 x 3 x 2 x 1 | = 4 x 3! | = 24 |
| 5 | 5 x 4 x 3 x 2 x 1 | = 5 x 4! | = 120 |
| 6 | и так далее | и так далее |
Для точного определения факториала любого числа следует воспользоваться таблицей факториалов
9! равно 362.880. Попробуйте посчитать 10!
10! = 9!х10
10! = 362.880 х 10 = 3.628.800
ФОРМУЛА ФАКТОРИАЛА
Существует правило как найти n факториал:
ФАКТОРИАЛ 0
Это очень интересная тема. Принято, что 0! = 1. А почему?
Никакое умножение чисел не приводит к 1, но давайте проследим факториалы в обратном порядке, скажем, от 4!:
И во многих задачах 0! = 1 просто имеет смысл.
ФАКТОРИАЛ ОТРИЦАТЕЛЬНОГО ЧИСЛА
Можем ли мы найти факториалы для чисел меньших нуля?
Нет. Факториалы для таких чисел не определены.
Почему? Легко объяснить на примере.
Начнем с 3! = 3 × 2 × 1 = 6 и спускаемся вниз:
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(поэтому 0! = 1)
(−1)! = 0! / 0 = 1 / 0 = ой, деление на ноль не определено
И с этого момента все целочисленные факториалы не определены.
ФАКТОРИАЛ ДРОБНОГО ЧИСЛА
Можем ли мы найти факториалы для таких чисел, как 0,4 или −8,116?
Да мы можем! Но нам нужно углубиться в тему под названием Гамма-функция, которая выходит за рамки этой страницы.
И они могут быть отрицательными (кроме целых чисел).
Вот несколько значений дробных факториалов:
| (-1/2)! | √π |
| (1/2)! | (1/2)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
ПРИМЕНЕНИЕ ФАКТОРИАЛА
Факториалы незаменимы для вычисления количества перестановок, сочетаний и размещений.
Что такое 100! / 98!
Используя наши знания из предыдущего примера, мы можем сразу перейти к следующему:
100!/98! = 100 × 99 = 9900
Другие примеры задач с факториалом и их решение на странице решение факториалов.
ИНТЕРЕСНЫЕ ФАКТЫ
100 факториал: 100! приблизительно 9,3326215443944152681699238856 x 10 157
200 факториал: 200! приблизительно 7,8865786736479050355236321393 x 10 374
Факториалы натуральных чисел
Факториал натурального числа n (обозначение – “n!“) равен произведению всех натуральных чисел от 1 до n включительно.
n! = 1 * 2 * 3 * 4 … * n
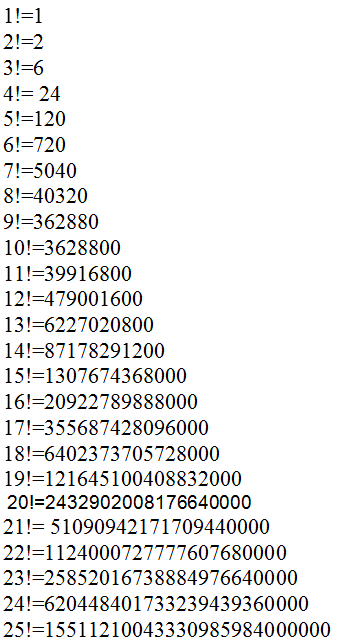
Ниже представлены таблицы с факториалами чисел от 1 до 20 (точные значения) и от 21 до 100 (приближенные значения).
1. Факториалы чисел от 1 до 20
| Значение | |
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40320 |
| 9! | 362880 |
| 10! | 3628800 |
| 11! | 39916800 |
| 12! | 479001600 |
| 13! | 6227020800 |
| 14! | 87178291200 |
| 15! | 1307674368000 |
| 16! | 20922789888000 |
| 17! | 355687428096000 |
| 18! | 6402373705728000 |
| 19! | 121645100408832000 |
| 20! | 2432902008176640000 |
2. Факториалы чисел от 21 до 100
Факториал – это быстрорастущая функция, и начиная с определенного n значения достаточно велики. Поэтому в математических вычислениях удобнее пользоваться приближенными значениями для больших чисел.
Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел. Формула факториала:
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.