Фигуры хладни что это
Фигуры Хладни
Published date 28.04.2015
Last modified date 14.01.2019
Существует несколько способов демонстрации стоячей волны, один из них – фигуры Хладни:
Согласно принципу Арнольда Эрнст Хладни – не первооткрыватель, впервые появление узоров наблюдал Роберт Гук. Но тем не менее в историю рисунок образующийся из-за стоячей волны в пластинке носит имя Хладни. Узор получали посыпая пластинку песком и проводя по краю смычком (википедия):
Движения смычка заставляли пластинку колебаться на некоторой резонансной частоте. Пластинка колеблется волнами, волна добегая до края отражается от него и бежит обратно, интерферируя сама с собой. В установке на фото пластинка колеблется под действием электромагнита. Если подобрать частоту так, чтобы на ней укладывалось целое число полуволн, то сформируется рисунок:









Образуется стоячая волна – на пластинке есть участки где прямая и отраженная волна вместе складываются усиливаясь – там песок всегда скачет, а есть там где они друг друга гасят – это узлы, в них песок лежит неподвижно. В зависимости от формы пластинки – фигуры могут быть различной формы. Взять пластинку произвольной формы, посыпать песком, подобрать частоту – и готовы логотипы для брендов)
Так как я видео красивое не сниму, приведу чужое:
А вот еще одно, с другими красивыми опытами:
Разумеется образование стоячей волны важно в конструировании музыкальных инструментов. Вот пример фигур Хладни на корпусе гитары (википедия):
Тут важно отметить, что на видео и на рисунках для простоты указаны частоты округленные до целых, в то время как для образования фигуры важны даже доли герца! Вращая ручку генератора не так просто поймать момент с устойчивым рисунком, особенно когда частота довольно высока.
Ну и для любителей загадок есть такая история. В Шотландии есть рослинская капелла св. Матвея, которая содержит множество тайн и загадок, и еще больше легенд связано с ее именем. В частности на одной из арок есть 213 резных каменных кубов, с вырезанных на них геометрическим рисунком. Многие исследователи пытались понять что зашифровано в рисунках на кубах. Отставной генерал ВВС Томас Митчел, со своим сыном пианистом Стюартом Митчелом предложили оригинальный способ расшифровки послания. Они сопоставили геометрические рисунки с фигурами Хладни, и пришли к выводу что на кубах записаны частоты – ноты.
Собрав ноты воедино и творчески обработав их они представили миру произведение – “Рослинский Мотет”
Если вы хотите поразвлекаться с фигурами Хладни, показать опыт на вечеринке – то вам нужно раздербанить динамик (инструкция) и закрепить на нем пластинку. В качестве генератора можно использовать любой программный генератор сигналов, а вот усилитель придется временно позаимствовать из активной акустики или собрать самостоятельно (можно даже обнаглеть и просто включить динамик в питание через mosfet транзистор, на выходе будет не синусоида, но фигуры Хладни получатся. В установке что на фото в начале поста – выход меандр, а не синус).
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Фигуры Хладни. О чём это?
О влиянии звука на тело и сознание человека сегодня уже слышали многие. Даже существует мнение, что западная низкочастотная музыка специально была создана для того, чтобы воздействовать на тело и сознание человека. И поведение людей на концертах такой музыки говорит само за себя – отмечается возбуждение нервной системы, раздражённость, агрессивность и так далее. Именно так воздействуют на человека низкие частоты, чего нельзя сказать о классической музыке, в которой преобладают высокочастотные звуки. И такая музыка исцеляюще воздействует на человека.
Звук – своего рода живая энергия, которую можно не только услышать, но и… увидеть. Да, именно так. Благодаря изобретению одного талантливого учёного это стало возможным.
Немецкий учёный, Хладни Эрнст Флоренс Фридрих ещё в 18-ом веке изобрёл способ, благодаря которому звук можно увидеть. Надо сказать, что немецкий физик не был первооткрывателем в этой области. Впервые особенность звука оказывать воздействие на окружающие предметы отметил английский учёный Роберт Гук ещё в 1680-ом году. Его исследования, которые он проводил в Оксфордском университете, показали, что предметы способны менять свою форму под воздействием колебаний.
Как именно это произошло? Роберт Гук отметил, что если воздействовать смычком на край металлической пластины, которая покрыта мукой, то мука начинает движение и постепенно формирует узоры.
Немецкий физик Эрнст Хладни продолжил работать в этом направлении. По мере того, как он накопил определённый опыт в этой сфере, он издал книгу «Теория Звука», в которой подробно описал свои эксперименты.
Эксперимент Хладни
В чём же важность и ценность проведённых Эрнстом Хладни исследований? Во-первых, как говорил сам Хладни, благодаря его исследованию появилась возможность «звук не только слышать, но и видеть».
Во-вторых, он эмпирическим путём доказал существование стоячей звуковой волны, которая собственно и формирует все эти диковинные узоры. Но самое главное, эксперимент Эрнста Хладни наглядно показывает, как сильно отличаются низкие и высокие звуковые вибрации.
Суть эксперимента в том, что при низких вибрациях формируются самые грубые простые узоры – геометрические фигуры: квадраты, кресты, круги и иже с ними. Но по мере повышения вибрации звука происходит настоящее чудо: на пластинах вырисовываются всё более сложные узоры – звёзды, орнаменты и так далее.
И это яркий пример того, как разные звуковые вибрации могут воздействовать на окружающий мир. И значит, воздействие звука на человека – это вовсе не миф. Ведь если под действием вибраций песок перемещается по пластине, образуя те или иные узоры, значит, некие процессы также проходят и на клеточном уровне в теле человека – клетки также реагируют на те или иные вибрации. И совершенно очевидно, что низкие и высокие вибрации действуют на человека не одинаково. Именно этим объясняется такая разница ощущений на концерте рок-музыки и на концерте классической музыки.
Фигуры Хладни в домашних условиях
Всё это может показаться какой-то фантастикой. Но главное преимущество науки в том, что любой желающий может повторить тот или иной эксперимент и убедиться в том, что это не миф, а реально существующий факт. Эксперимент с фигурами Хладни можно повторить в домашних условиях. Что нам для этого потребуется?
Как сделать фигуры Хладни в домашних условиях? Для этого нам потребуется металлическая пластина, закреплённая по центру, а также скрипичный смычок. Скрипичный смычок в данном случае будет наиболее удобным, но может подойти альтовый, виолончельный и контрабасовый. Также нам потребуется некий мелкодисперсный порошок, в классическом варианте используется песок, но проще будет использовать то, что найдётся на кухне – манную крупу, соль или соду. Сахар, скорее всего, не подойдёт, так как имеет слишком крупные кристаллы.
Для проведения эксперимента нам необходимо будет насыпать на поверхность пластины песок, манку или соль, а затем проводить по торцу пластины смычком. Пластина будет издавать звуковые вибрации, и на наших глазах под воздействием этих вибраций будет формироваться рисунок.
Важно отметить, что пластины квадратной формы при воздействии смычка будут издавать низкие вибрации, а вот пластины круглой формы – более высокие. Поэтому, если есть желание и возможность увидеть именно разницу между низкими и высокими вибрациями, необходимо повторить эксперимент на квадратной и на круглой пластине. Звук, издаваемый квадратной пластиной, будет формировать более примитивные узоры, а звуки на круглой пластине – более замысловатые.
В классическом варианте в лабораторных условиях уже не используется смычок, как это делал сам Эрнст Хладни. С начала 20-го века для эксперимента с фигурами Хладни стали использовать громкоговоритель с генератором звука под самой пластиной. Это позволяет механизировать процесс, а самое главное – чётко регулировать частоты воспроизводимого звука и наблюдать за переменами в рисунке при минимальных изменениях в воспроизводимых частотах.
Эксперимент Хладни даёт ответы на вопросы
Помимо того, что фигуры Хладни наглядно демонстрируют тот факт, что звук способен влиять на окружающий мир и в том числе на человека, это открытие позволяет по-новому взглянуть на археологические находки. Учёные много лет ищут ответ на вопрос: как древним людям, которые согласно официальной исторической версии были дикарями и кроме каменного топора сделать ничего не могли, всё же удавалось строить такие удивительные сооружения. Примерами могут быть гробницы, древние храмы и так далее.
Эксперимент Хладни приоткрывает завесу тайны в этом вопросе. Не исключено, что уже задолго до открытия немецкого физика наши предки знали о чудодейственных
способностях звука и его возможности воздействовать на материю. Возможно, они нашли способ с помощью звуковых вибраций гравировать те сложные рисунки, которые часто вводят в недоумение археологов. В самом деле, уж явно не с помощью пресловутого каменного топора или «палки-копалки» были сделаны эти диковинные узоры. И эксперимент Хладни позволяет задуматься о том, что, возможно, наши предки были гораздо более развитыми, чем мы привыкли думать.
Ну и самое главное, эксперимент Хладни позволяет увидеть, что низкие и высокие звуковые вибрации действуют на материю по-разному. И это ещё раз доказывает, что низко-вибрационная музыка, которая сейчас как раз таки наиболее популярна, огрубляющим образом воздействует как на материю, так, очевидно, и на сознание. А музыка с высокими вибрациями, способная создавать сложные узоры, скорее всего, на тело и сознание действует исцеляющим образом.
Фигуры хладни что это
Звук имеет формирующую силу.
Звук вдребезги разбивает стаканы и формирует узоры на песке.
Формирующую силу звука можно легко продемонстрировать. Необходимо рассыпать немного тонкого песка на корпус скрипки (или гитары) и слегка, так чтобы песок не рассыпался, провести смычком по одной из струн (дернуть струну). Вы сразу увидите, что вибрация имеет формирующий эффект, поскольку как только тронутая струна зазвучит, и звук взятой ноты станет усиливаться, песок начнет собираться, образуя различные геометрические формы, например квадрат, который будет виден вполне отчетливо, или треугольник, или эллипс; возможно появление какого-либо замысловатого, необычайно красивого узора, напоминающего снежинку.
Аналогичный эксперимент можно провести, используя лист стекла, на котором рассыпанный песок также начнет собираться и образовывать фигуры, формы которых будут зависеть от силы движения смычка и силы, с какой смычок прижимается к краю стекла. Причем формы получаемых фигур будут разные; если взять на скрипке глубокую мягкую ноту, получится одна фигура, если визгливую или похожую на долгий пронизывающий крик — другая; стаккато ведет к появлению одной формы, медленное вибрато — другой.
ХЛАДНИ Эрнст Флоренс Фридрих (1756-1827)
ХЛАДНИ (Chladni) Эрнст Флоренс Фридрих (1756-1827), немецкий физик, основатель экспериментальной акустики, иностранный член-корреспондент Петербургской АН (1794). Исследовал формы колебаний различных тел; описал фигуры, названные его именем. Указал на космическое происхождение метеоритов.
Хладни первым предпринял экспериментальные исследования различных акустических явлений, многие из которых получили теоретическое объяснение значительно позже.
В 1787 году описал фигуры, образующиеся на посыпанной песком поверхности упругой колеблющейся пластинки (фигуры Хладни)
Хладни фигуры, фигуры, образуемые скоплением мелких частиц сухого песка вблизи узловых линий на поверхности упругой колеблющейся пластинки или подобной ей механической системы; каждому собственному колебанию пластинки соответствует своё расположение узловых линий. Х. ф. названы по имени обнаружившего их Э. Ф. Ф. Хладни.
В случае круглой пластинки узловые линии могут быть круговыми или радиальными; в случае прямоугольной или треугольной пластинки они имеют направление, параллельное сторонам или диагоналям. Меняя точки закрепления и места возбуждения, можно получить разнообразные Х. ф., соответствующие различным собственным колебаниям пластинки. Х. ф. применяются для изучения собственных частот диафрагм телефонов, микрофонов, громкоговорителей.
Влияние звука на сознание.
Использование звука и музыки для исцеления возникло в самом начале истории человечества. Документально подтверждено, что шаманы и целители аборигенных народов, использующие такие инструменты, как человеческий голос, флейты, барабаны и другие ударные, способны изменять состояние мозга (то есть менять нейрологическую активность мозга). Опыты показали, например, что некоторые ритмы барабанов усиливают тета-активность, связанную с гипнотическими и близкими к сновидению состояниями сознания, а также с вдохновением и повышенным уровнем творческой активности.
Изучение нейрологического влияния звука показало, что человеческий мозг реагирует на чистые звуки вполне определенным образом. Позитронная томография, измеряющая уровень поглощения глюкозы на клеточном уровне, показала, что чистые звуки и музыка без слов стимулируют повышение клеточной активности в правом или «недоминантном» полушарии.
При стимуляции недоминантного полушария (например, с использованием чистого звука) часто возникают необычные состояния сознания. Это происходит от того, что недоминантное полушарие включает пространственный и интуитивный аспекты нашего сознания. В таких нейрологических состояниях наше восприятие реальности (как внутренней, так и внешней) может сильно отличаться от нашего повседневного восприятия. Наши чувства могут обостриться, их восприятие становится более живым и утонченным. Довольно часто люди испытывают прямое переживание своей внутренней ментальной и эмоциональной жизни через прямое восприятие своих психических мотивов (то есть глубинных эмоций, фантазий и архетипичных конфликтов и драм). Они могут проявляться как внутренние видения (похожие на сновидения картинки) или даже как внутренний диалог.
Хотя наша западная культура в основном не интересуется такими глубокими эмоциональными и ментальными состояниями, многочисленные случаи из жизни великих ученых и людей искусства указывают, что такие состояния сознания являются вратами нашего прирожденного гения.
Букварь волн мозга.
От тета мы поднимаемся к альфа, частоте, связанной с легким расслаблением. Диапазон альфа 8-14 Hz, и ее часто используют в методах ускоренного обучения, а также некоторых разновидностях техник селф-хелпа.
Использование определенных состояний мозга позволяет улучшить внутреннюю активность, например обучение, самоисцеление, изучение измененных состояний сознания и т.д. Хотя измерение активности мозга крайне важно для понимания нейрофизиологии, собственно ментальные, эмоциональные и духовные переживания человека важны для нашего понимания взаимодействия мозга и разума.
Азы акустики.
Ниже изложен базовый минимум информации о звуковых частотах в том смысле, в каком этот термин используется в психоакустике. Любая звуковая вибрация состоит из волновых форм. На диаграмме изображена синусоида (это самая типичная форма волны, используемой в психоакустике).
Есть несколько возможных вариантов использования определенных частот для «приведения» мозга в измененное состояние. Важно помнить, что большинство людей не слышат низкие частоты, типичные для волн мозга. Например, низкая альфа (и соответствующее ей расслабление) находится в диапазоне 8-9 Hz, за пределами порога слышимости (20 Hz).
Говоря о работе мозга и восприятии тела, один из аспектов работы с частотами крайне интересен для психоакустики. Используя различные частоты, можно вызвать резонанс в различных частях тела, таким образом активизируя эмоциональную/ментальную активность, связанную с этим местом. Этому можно найти очень интересное применение в психотерапии и дисциплинах, занимающихся связью ума и тела.
Теоретические схемы технологии акустического изучения мозга (Acoustic Brain Research, ABR)
Что такое психоаккустика?
Звук и музыка.
Музыка и звуки веками использовались для целительства и трансформации. От гортанных заговоров шаманов древности до возвышенного григорианского пения в кафедральных соборах, звук и музыка играли важную роль в человеческой культуре. Мы только недавно начали понимать физиологическое воздействие звука и музыки на мозг. Далее мы поговорим о его основе и различных применениях в технологии психоакустики.
Мы знаем, что музыка может сильно влиять на работу мозга. Это подтверждают работы д ра Лозанова (Dr. Lozanov) из Болгарии. Он обнаружил, что музыка с темпом 60 ударов в минуту (как, например, Largo в музыке периода барокко) на 6% усиливает альфа-активность (связанную с расслаблением), при этом на 6% процентов уменьшая бета-активность (связанную с нормальным бодрствующим сознанием). При этом пульс замедляется в среднем на 4 деления ртутного столбика, и люди говорят о «состоянии расслабленного сознания».
Затем д-р Лозанов обнаружил, что может ускорить процесс обучения, используя музыку в таком ритме. В Америке его метод стал известен как Суперобучение (Superiearning). Д-ру Лозанову стало ясно, что ритм музыки оказывает мощное влияние на мозг. В процессе работы он обнаружил, что тембр, или тональность музыки, также оказывает сильное влияние на работу мозга. Мы в ABR используем этот принцип; на каждой кассете записана музыка с ритмом и тембром, подходящими для получения желаемого эффекта.
Д-р Сью Чапмэн (Dr. Sue Chapman) провела эксперимент в Городской больнице Нью Йорка, изучая влияние музыки на младенцев, родившихся недоношенными. Одна группа младенцев слушала Колыбельную Брамса (вариацию для струнных инструментов) шесть раз в день, а другая группа (контрольная) не слушала никакой музыки. Новорожденные, слушавшие Брамса, быстрее набирали вес, меньше страдали от осложнений и были выписаны из больницы в среднем на неделю раньше тех, кто не слушал музыку.
Что произошло?
Эти исследования показали, что музыка действительно создает некую разновидность языка. Как в любом языке, здесь сесть свой синтаксис. Как правило, понятие синтаксиса применяется к записанной или устной речи и означает порядок построения предложения. Изменив порядок слов в предложении, вы измените и смысл. Эту концепцию можно применить и к музыке. Если вы переставите местами ноты, вы измените произведение. Порядок информации (нот) в музыке так же важен, как порядок информации (слов) в речи. Если считать музыку языком, или информацией, то это откроет новые возможности для понимания ее влияния на мозг.
Сам того не подозревая, аббат отнял у монахов важную форму стимуляции мозга. Лишившись слуховой стимуляции григорианского пения, центральная нервная система монахов подверглась депрессии. Когда д-р Томатис уговорил настоятеля вернуть песнопения, депрессия прекратилась, и монахи выздоровели. Этот случай заставил д-ра Томатиса начать изучать влияние звука на мозг. В процессе работы он обнаружил влияние высоких частот на работу мозга, эмоциональные проблемы и трудности в обучении.
С помощью звука, например, известный исследователь, музыкант, певец, целитель и писатель Том Кенион, создал методы, которые ускоряют лечебную терапию и положительные изменения в организме.
ТЕХНОЛОГИИ, ИНЖИНИРИНГ, ИННОВАЦИИ
Измеритель диаметра, измеритель эксцентриситета, автоматизация, ГИС, моделирование, разработка программного обеспечения и электроники, БИМ
Хаос: эффект бабочки, фигуры Хладни и тайны мироздания

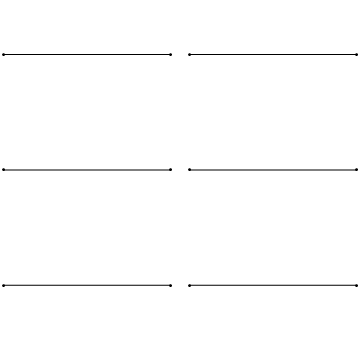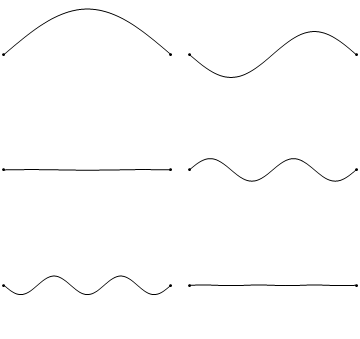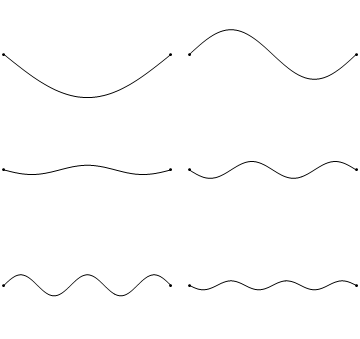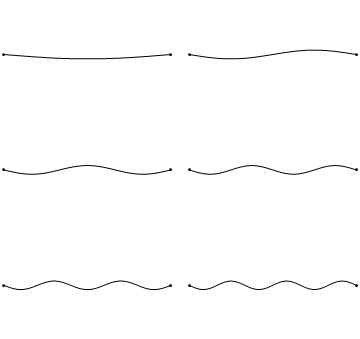
Тем не менее, колебания любого упругого тела можно представить как комбинацию накладывающихся друг на друга более простых нормальных колебаний. Вот так выглядят несколько нормальных колебаний простейшего упругого тела – одномерной натянутой струны.
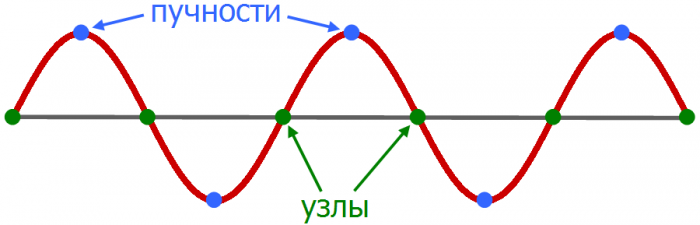
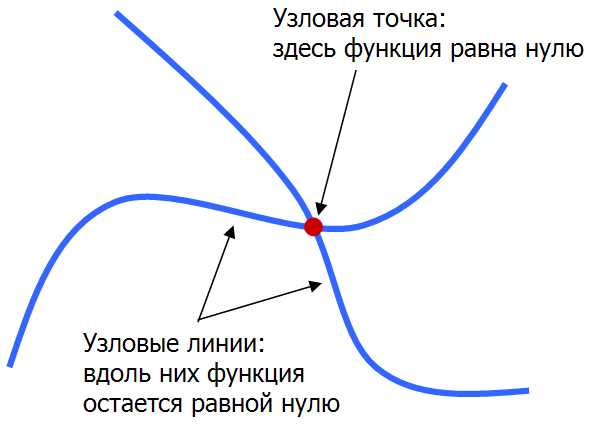
Каждое нормальное колебание представляется стоячей волной, которая, в отличие от бегущей волны, стоит на месте и обладает своим рисунком распределения амплитуд колебаний по пространству. На этом рисунке можно выделить пучности – точки, где амплитуда колебаний достигает максимумов, и узлы – неподвижные точки, в которых амплитуда колебаний равна нулю.
Кроме того, каждая такая волна колеблется со своей собственной частотой. В случае струны, как можно заметить, частота колебаний стоячей волны увеличивается с ростом числа узлов и пучностей.
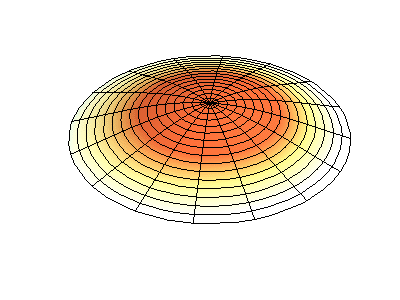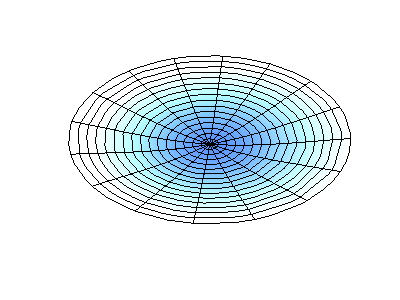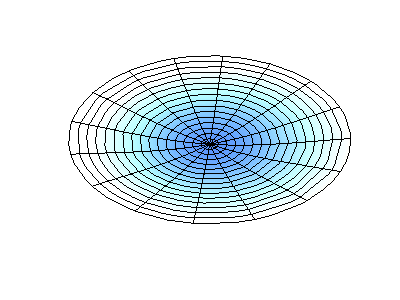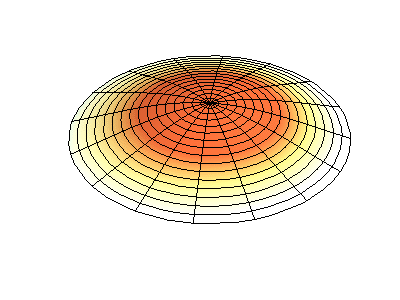
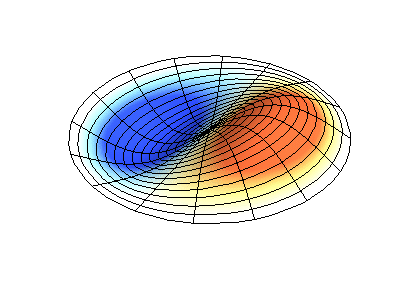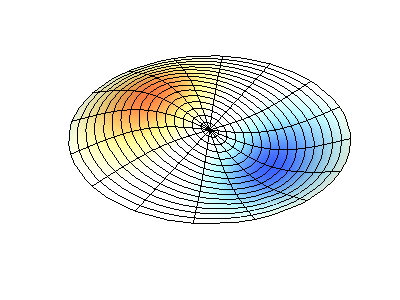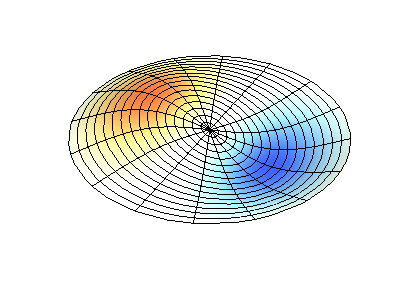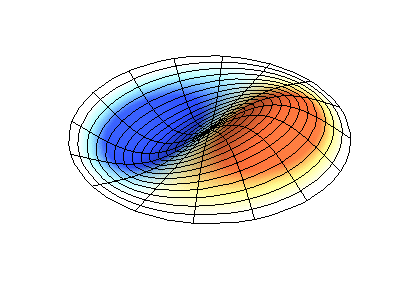
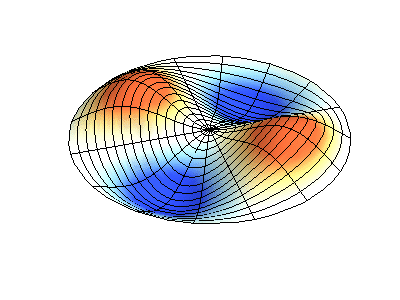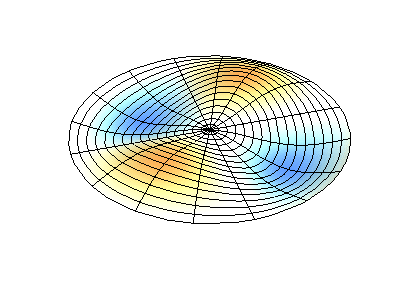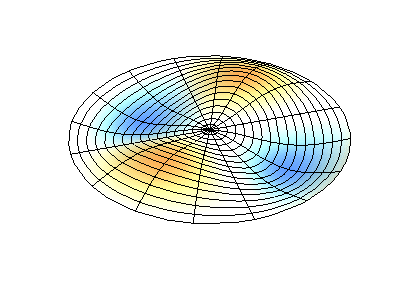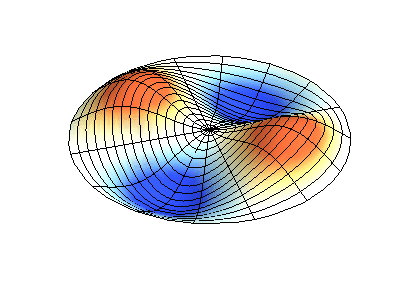
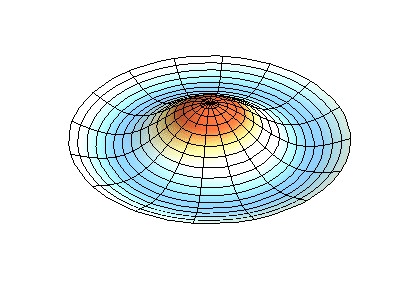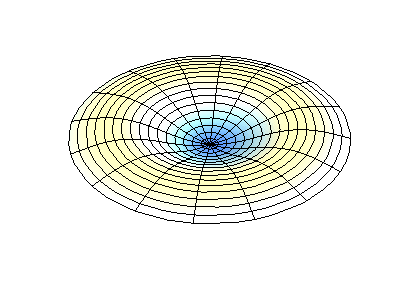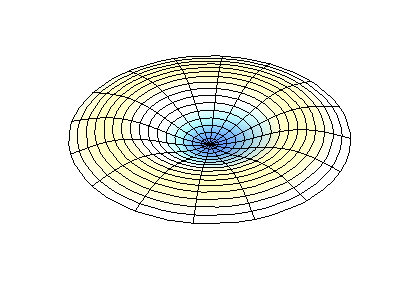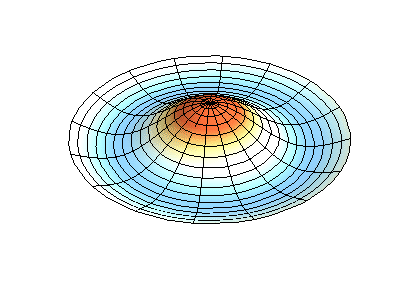
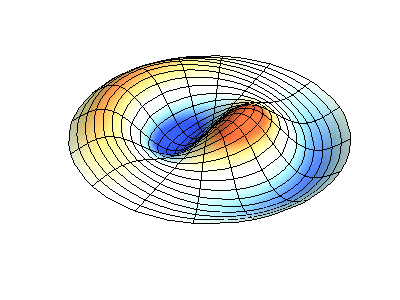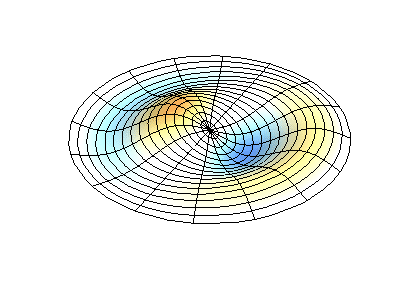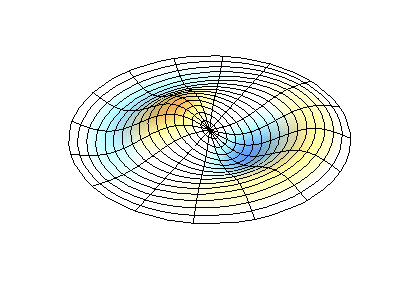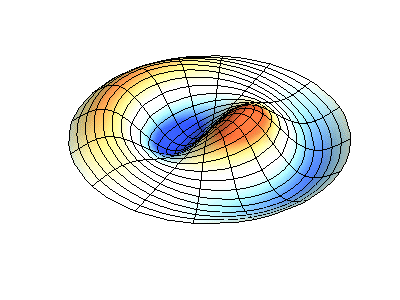
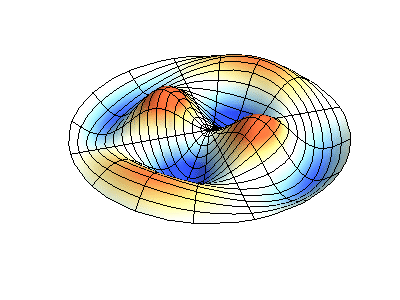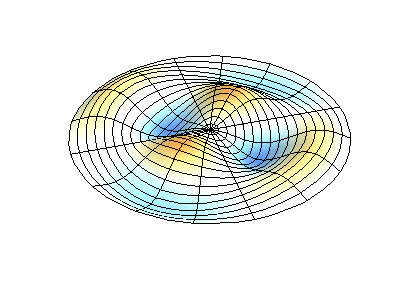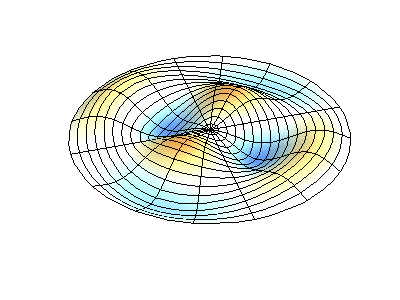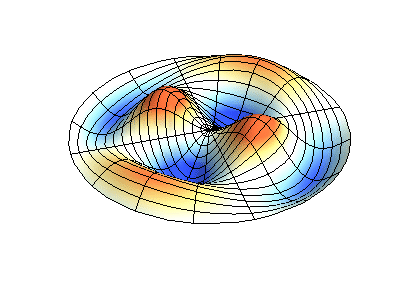
Посмотрим теперь на двумерную систему, примером которой может служить тонкая упругая мембрана, натянутая на жесткую рамку. Нормальные колебания круглой мембраны выглядят сложнее, чем в случае струны, а вместо отдельных точек-узлов имеются узловые линии, вдоль которых мембрана неподвижна.
Нормальные колебания круглой мембраны с закрепленными краями. Источник.
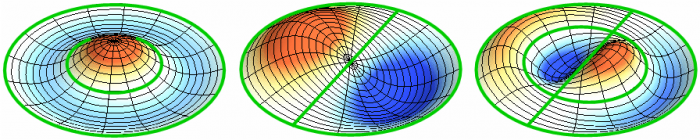
У круглой мембраны узловые линии, представляющие собой окружности и отрезки вдоль радиусов, могут пересекаться под прямыми углами. Если же края мембраны имеют произвольную форму, нахождение частот нормальных колебаний и картин их узлов и пучностей превращаются в задачу, решаемую только с помощью компьютера.
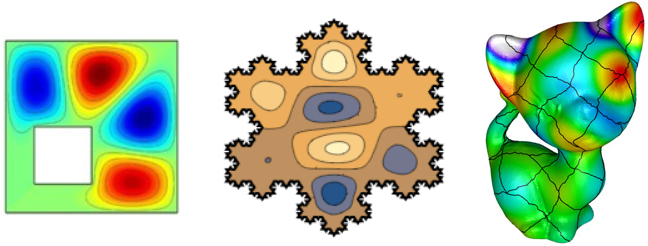
Уравнения, описывающие колебания тонкой упругой пластинки, отличаются от уравнений колебания мембраны, поскольку пластинка обладает собственной жесткостью, в то время как мембрана мягкая и пружинит лишь за счет натяжения внешними силами. Однако здесь тоже существуют наборы нормальных колебаний, рисунки которых существенным образом зависят от формы границ.
Фигуры Хладни
Как было сказано выше, в общем случае колебания тела представляют собой комбинацию целого набора возбужденных в нем нормальных колебаний. Явление резонанса позволяет выборочно возбудить какое-то одно нужное нам нормальное колебание – для этого следует раскачивать тело при помощи внешней силы с частотой, равной собственной частоте нормального колебания.
На двух видео ниже показана типичная схема получения фигур Хладни: упругая пластинка прикрепляется в центре к генератору механических колебаний, частоту которых плавно увеличивают. Нормальные колебания пластинки со своими картинами узлов и пучностей возбуждаются при резонансном совпадении частоты генератора с собственными частотами этих колебаний (собственные частоты показаны на видео в левом нижнем углу).
Здесь версия этого же видео, на которой частоты нормальных колебаний можно оценить на слух.
А здесь немного красивее.
Картины узлов и пучностей мы видим благодаря тому, что воздушные потоки вблизи колеблющейся пластинки сдувают песчинки к узловым линиям стоячей волны (*). Таким образом, фигуры Хладни показывают нам картины узловых линий нормальных колебаний упругой пластинки.
(*) Если размер частичек, насыпанных на пластинку, достаточно мал, то их будет сдувать уже не к узлам, а к пучностям стоячей волны, как было показано в этой экспериментальной работе.

Еще пример нормальных волн – это стоячие волны на поверхности воды. Они описываются уравнением, отличающимся от уравнений колебания пластинок и мембран, но следуют таким же качественным закономерностям, и с их помощью можно получать аналоги фигур Хладни.
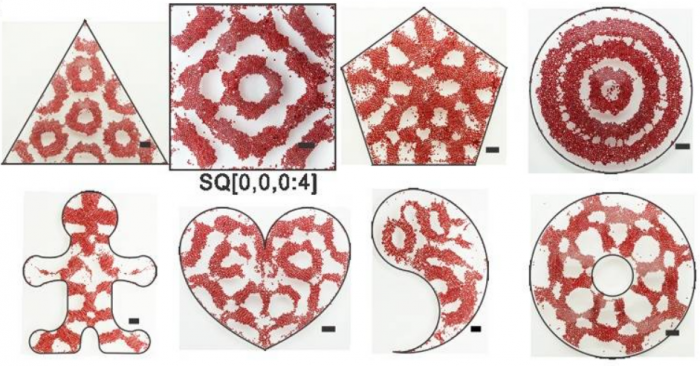
Классический хаос
Итак, мы видели, что в случае круглой мембраны узловые линии – теоретически! – замечательно пересекаются, в то же время на фигурах Хладни на квадратных или более сложных пластинках узловые линии избегают пересечений. Чтобы понять причину этих закономерностей, нам придется сделать небольшой экскурс в теорию хаоса.
Классический хаос – это свойство механических систем, заключающееся в чрезвычайно сильной зависимости траектории их движения от изменений начальных условий. Эта зависимость известна также как «эффект бабочки». Яркий пример хаотического поведения можно встретить при попытках предсказания погоды: система уравнений, описывающая движение атмосферы и океанов, не позволяет дать достаточно точные прогнозы на больших временах из-за экспоненциально нарастающих ошибок, обусловленных малыми неточностями исходных данных.
(**) Хотя на обывательском уровне слова «хаотичный» и «случайный» часто используются как синонимы, на уровне физики эти понятия существенно отличаются: хаотические системы являются детерминированными – это системы, движение которых описывается строго определенными уравнениями, не подвержено воздействию случайных факторов и потому предопределено начальными условиями. Однако трудность предсказания движения хаотических систем делает их на практике похожими на случайные.
Явление хаоса было открыто и популяризовано метеорологом и математиком Эдвардом Лоренцем, обнаружившим, что два расчета прогноза погоды, начинающиеся с очень близких начальных условий, сначала почти неотличимы друг от друга, но с какого-то момента начинают кардинально расходиться.
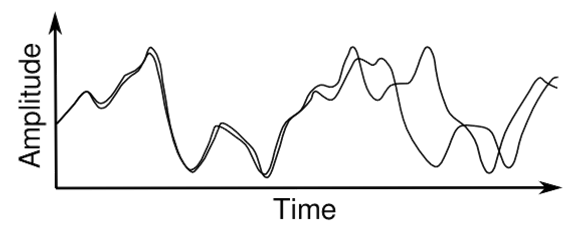
Простейшими системами, на примере которых удобно изучать хаос, являются бильярды – участки плоской поверхности, по которым без трения может катиться шарик, абсолютно упруго отскакивающий от жестких стенок. В хаотических бильярдах траектории движения шарика, имеющие незначительные отличия в самом начале, в дальнейшем существенно расходятся. Пример хаотического бильярда – изображенный ниже бильярд Синая, представляющий собой прямоугольный бильярд с круговым препятствием в центре. Как мы увидим, именно за счет этого препятствия бильярд становится хаотическим.
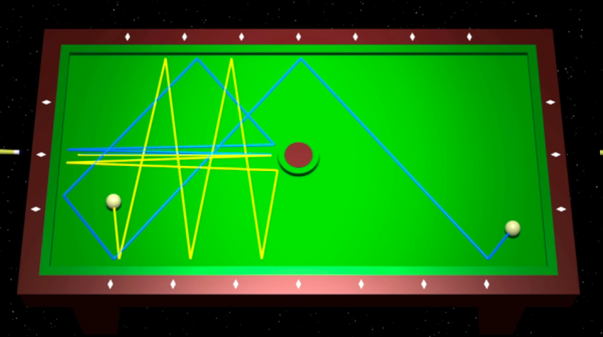
Интегрируемые и хаотические системы
Механические системы, не являющиеся хаотическими, называются интегрируемыми, и на примере бильярдов можно наглядно увидеть разницу между интегрируемыми и хаотическими системами.
Прямоугольный и круглый бильярды являются интегрируемыми благодаря своей симметричной форме(***). Движение шарика в таких бильярдах – это просто комбинация двух независимых периодических движений. В прямоугольном бильярде это движения с отскоками от стенок по горизонтали и по вертикали, а круглом это движение вдоль радиуса и угловое движение по окружности вокруг центра. Такое движение легко просчитываемо и не показывает хаотического поведения.
(***) Еще один пример интегрируемого бильярда – это бильярд в форме эллипса. В этом случае симметрия, делающая его интегрируемым, уже не столь очевидна, как в случае круга и прямоугольника.
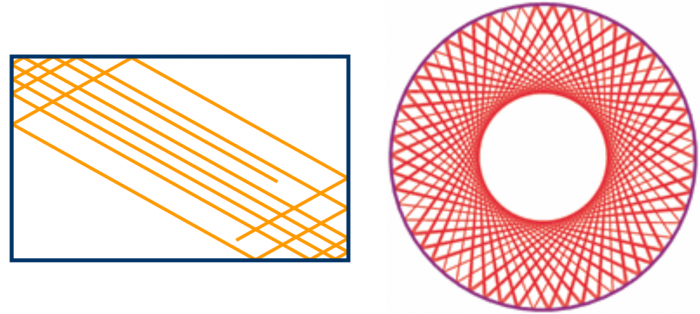
Бильярды более сложной формы, не обладающие столь высокой симметрией, как у круга или прямоугольника, являются хаотическими(****). Один из них мы видели выше – это бильярд Синая, в котором симметрия прямоугольника разрушается круговым включением в центре. Также часто рассматриваются бильярд «стадион» и бильярд в форме улитки Паскаля. Движение шарика в хаотических бильярдах происходит по весьма запутанным траекториям и не раскладывается на более простые периодические движения.
(****) Если выражаться более точно, то принадлежность бильярда к интегрируемым или хаотическим зависит от числа независимых интегралов движения – сохраняющихся с течением времени величин. Интегрируемые бильярды обладают двумя интегралами движения, в двумерной системе этого достаточно для точного аналитического решения уравнений движения. Хаотический бильярд имеет только один интеграл движения – кинетическую энергию шарика.
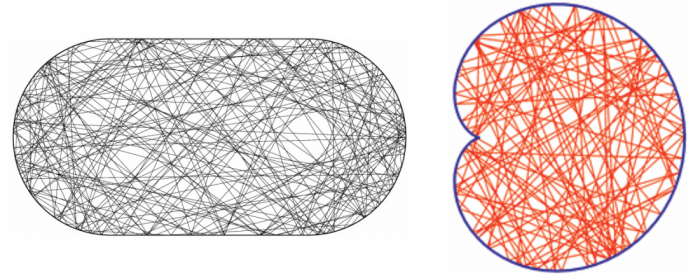
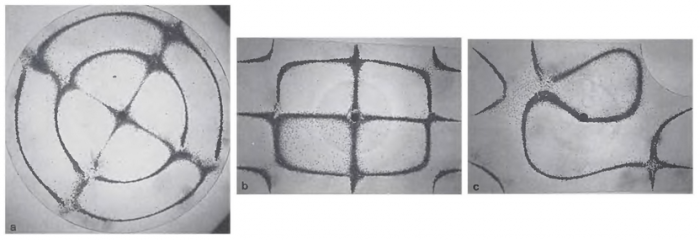
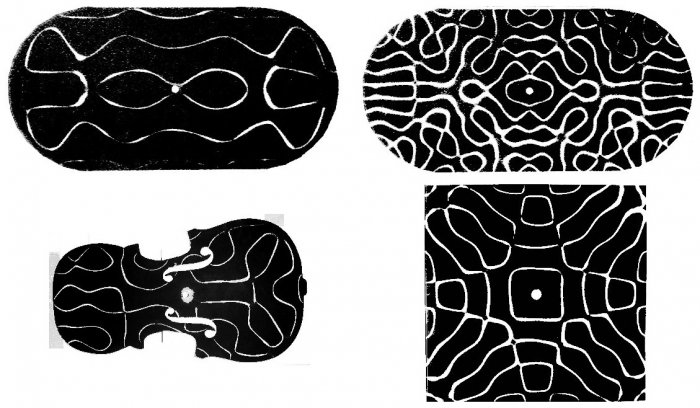
Здесь можно уже догадаться, что наличие пересечений между линиями на фигурах Хладни определяется тем, имеет ли пластинка форму интегрируемого или хаотического бильярда. Это наглядно видно на фотографиях ниже.

Квантовый хаос
Как же понять, почему наличие пересечений между узловыми линиями обусловлено интегрируемостью бильярда? Для этого нужно обратиться к квантовой теории хаоса, объединяющей теорию хаоса с механикой колебаний и волн.
Если в классической механике шарик в бильярде описывается в виде материальной точки, движущейся вдоль определенной траектории, то в квантовой механике его движение описывается как распространение волны, подчиняющейся уравнению Шредингера и отражающейся от стенок бильярда.
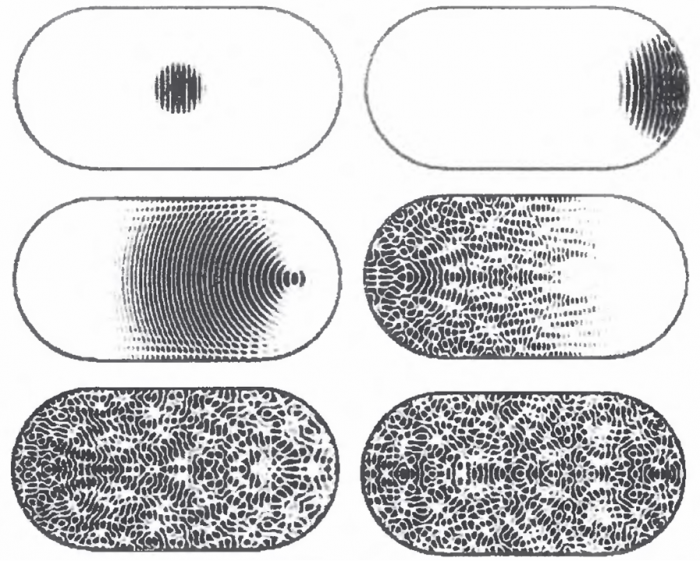
То же самое в виде анимации, но с немного другими начальными условиями.
Как и в случае колебаний мембран и пластинок, описывающее квантовый бильярд уравнение Шредингера позволяет найти нормальные колебания в виде стоячих волн, обладающие характерным рисунком узловых линий и пучностей, индивидуальным для каждого колебания и зависящим от формы границ.
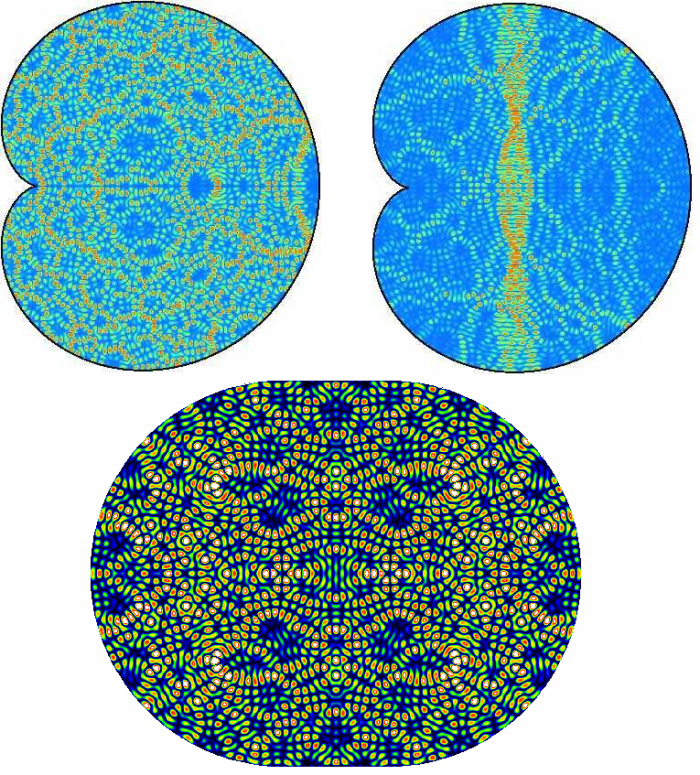
Рисунки стоячих волн в интегрируемых и хаотических квантовых бильярдах качественно отличаются: интегрируемые бильярды показывают симметричные, упорядоченные картины стоячих волн, в то время как в хаотических бильярдах рисунки стоячих волн весьма запутанные и не показывают никаких видимых закономерностей (в конце статьи будет показано, что некоторые интересные закономерности там все-таки существуют).

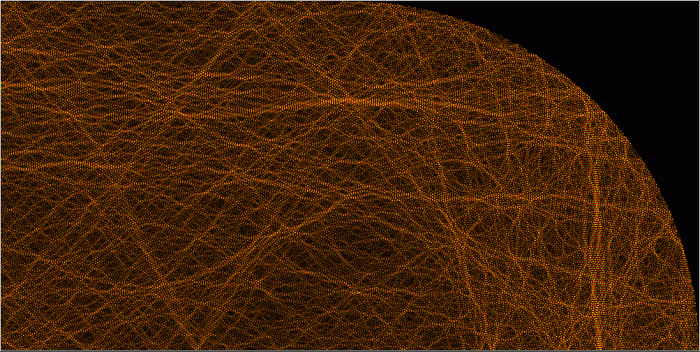
Качественное отличие видно и в картинах узловых линий: в случае интегрируемого квантового бильярда мы видим упорядоченные семейства взаимно пересекающихся линий, а в хаотических бильярдах эти линии, как правило, не пересекаются.
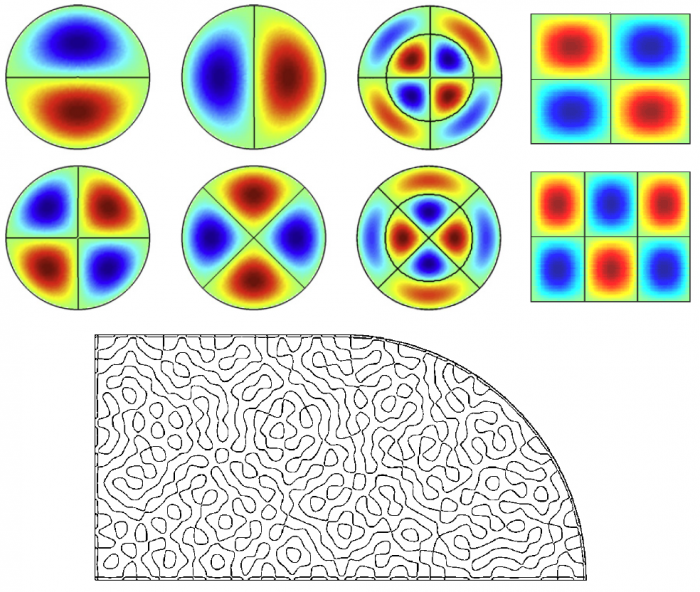
Пересекаться или не пересекаться?
Почему же узловые линии в хаотических бильярдах не пересекаются? В 1976 году математик Карен Уленбек доказал теорему, согласно которой узловые линии стоячих волн квантовых бильярдов, вообще говоря, и не должны пересекаться.
В упрощенном виде это можно показать следующим образом: допустим, что две узловые линии пересекаются в точке (x0,y0). Чтобы такое произошло, функция f(x,y), задающая зависимость амплитуды стоячей волны от координат, должна одновременно удовлетворять трем условиям:
Итого имеем три условия (или три уравнения), наложенные на функцию двух переменных f(x,y). Как мы знаем, одного уравнения недостаточно для полного нахождения двух неизвестных x и y, двух уравнений для этого уже достаточно, а три уравнения – это слишком много. Система трех уравнений для двух неизвестных, вообще говоря, решений иметь не будет, если только нам случайно не повезет. Поэтому точки пересечения узловых линий могут существовать только в порядке исключения.
В интегрируемых бильярдах такие исключения как раз и возникают. Как мы видели выше, их особые свойства – предсказуемость движения, отсутствие хаоса, регулярные рисунки стоячих волн – являются следствием их высокой симметрии. Эта же симметрия обеспечивает и одновременное выполнение трех условий, необходимое для пересечений узловых линий.
Давайте теперь более внимательно посмотрим на примеры фигур Хладни, типичных для интегрируемых и хаотических бильярдов. На рисунке ниже показаны три характерных случая. Слева пластинка имеет форму круга, поэтому соответствующий квантовый бильярд является интегрируемым, и узловые линии пересекаются между собой. В центре пластинка прямоугольная, что тоже соответствует интегрируемой системе, однако круглое крепление в центре слегка нарушает симметрию прямоугольника, поэтому узловые линии пересекаются не везде. Справа показан пример чисто хаотической системы: пластинка в форме четверти бильярда Синая (в верхнем правом углу есть круговой вырез), узловые линии на которой уже не пересекаются.
Таким образом, чем сильнее форма пластинки – с учетом ее крепления – отличается от формы интегрируемого бильярда (такого как круг или прямоугольник), тем меньше на ней пересечений узловых линий.
Получить красивые фигуры Хладни с пересекающимися линиями на круглой пластинке не так-то просто. При возбуждении колебаний с центральным креплением круговая симметрия всей системы запрещает формирование радиальных узловых линий, поэтому мы увидим лишь скучный набор окружностей (эту трудность можно обойти, возбуждая колебания не с центра, а с края пластинки при помощи смычка от скрипки). Если же пластинку закрепить не по центру, фигуры Хладни станут интереснее, но из-за нарушения круговой симметрии система перестанет быть интегрируемой.
Круглая пластинка, крепление по центру.
Круглая пластинка, крепление сдвинуто из центра.
А здесь разные варианты с круглыми и некруглыми пластинками.
Наконец, внимательный читатель может заметить: а я вижу, что иногда узловые линии пересекаются даже на «хаотических» пластинках. Как же так, если их пересечение запрещено теоремой Уленбека?
Во-первых, узловые линии могут избегать пересечения, но перед этим сближаться так сильно, что из-за конечной ширины дорожки песка нам будет казаться, что пересечение есть. Во-вторых, между интегрируемыми и хаотическими системами на самом деле не существует резкой границы.

В классической теории хаоса этому вопросу посвящена знаменитая теория Колмогорова-Арнольда-Мозера. Она говорит о том, что если слегка нарушить симметрию интегрируемой системы, то она не станет сразу же проявлять хаотическое поведение, а, по большей части, сохранит свое свойство предсказуемости движения. На уровне квантовой теории хаоса и фигур Хладни это проявляется в том, что в некоторых местах пересечения узловых линий сохраняются. Это происходит либо в особо симметричных точках бильярда, либо далеко от источника возмущения, нарушающего симметрию интегрируемой системы.
Что еще?
Чем еще интересна квантовая теория хаоса? Для заинтересованного читателя упомяну о трех дополнительных вопросах, уже не связанных непосредственно с фигурами Хладни.
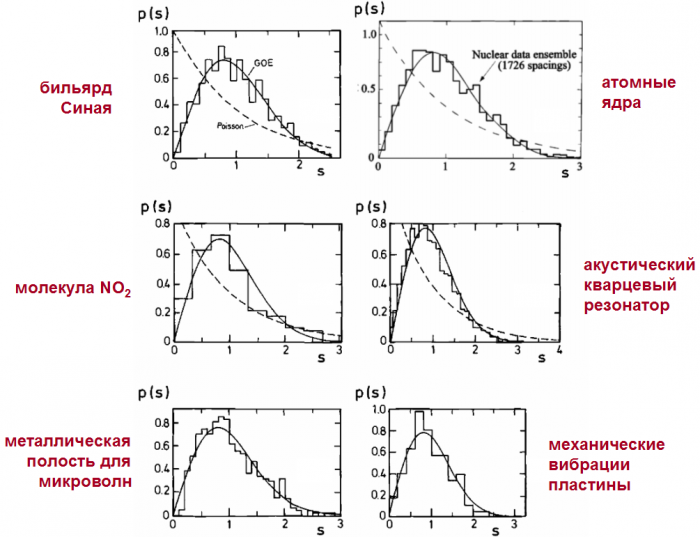
1) Важное явление, изучаемое этой теорией – универсальность хаотических систем. Подавляющее большинство систем, в которых могут возникать нормальные колебания, являются хаотическими, и все они – независимо от своей физической природы! – подчиняются одинаковым закономерностям. Феномен универсальности, при котором совершенно разные системы описываются одними и теми же формулами, сам по себе очень красив и служит нам напоминанием о математическом единстве физического мира.
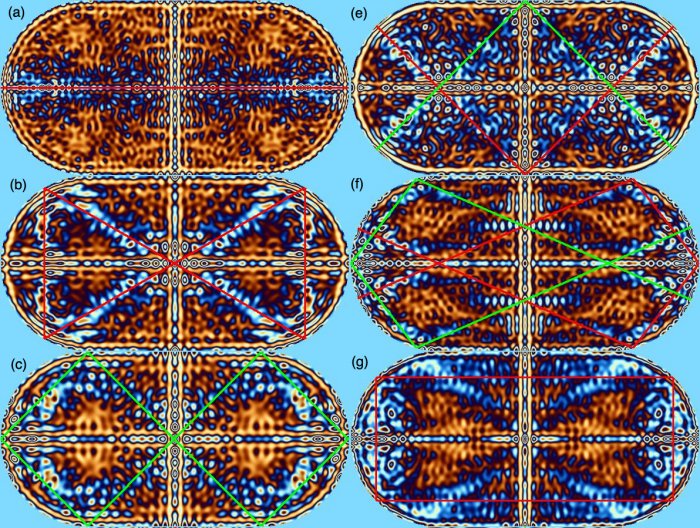
2) Рисунки нормальных колебаний хаотических бильярдов обладают интересной особенностью, называемой «квантовыми шрамами». Мы видели, что траектории движения шарика в хаотическом бильярде обычно выглядит весьма запутанными. Но есть и исключения – это периодические орбиты, достаточно простые и короткие замкнутые траектории, вдоль которых шарик совершает периодическое движение. Квантовыми шрамами называются резкие сгущения стоячих волн вдоль периодических орбит.
3) До сих пор мы говорили о двумерных системах. Если же рассматривать распространение волн в трехмерном пространстве, то здесь тоже могут возникать узловые линии, вдоль которых амплитуда колебаний равна нулю. Особенно важно это при изучении бозе-конденсации и сверхтекучести, где тысячи атомов движутся как единые «волны материи». Анализ структуры узловых линий волн материи в трехмерном пространстве необходим, например, для понимания того, как возникает и развивается квантовая турбулентность в сверхтекучих системах.

Если размер частичек, насыпанных на пластинку, достаточно мал, то их будет сдувать уже не к узлам, а к пучностям стоячей волны, как было показано в этой экспериментальной работе.
Хотя на обывательском уровне слова «хаотичный» и «случайный» часто используются как синонимы, на уровне физики эти понятия существенно отличаются: хаотические системы являются детерминированными – это системы, движение которых описывается строго определенными уравнениями, не подвержено воздействию случайных факторов и потому предопределено начальными условиями. Однако трудность предсказания движения хаотических систем делает их на практике похожими на случайные.
Еще один пример интегрируемого бильярда – это бильярд в форме эллипса. В этом случае симметрия, делающая его интегрируемым, уже не столь очевидна, как в случае круга и прямоугольника.
Если выражаться более точно, то принадлежность бильярда к интегрируемым или хаотическим зависит от числа независимых интегралов движения – сохраняющихся с течением времени величин. Интегрируемые бильярды обладают двумя интегралами движения, в двумерной системе этого достаточно для точного аналитического решения уравнений движения. Хаотический бильярд имеет только один интеграл движения – кинетическую энергию шарика.
Понравилась статья? Тогда поддержите нас, поделитесь с друзьями и заглядывайте по рекламным ссылкам!