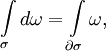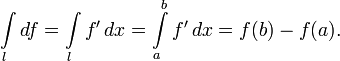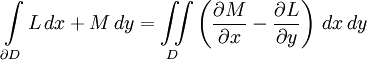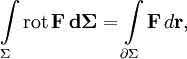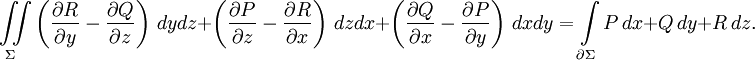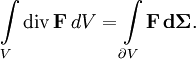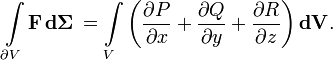Формула стокса что описывает

Как определить вязкость жидкости методом Стокса?

Формулу определения вязкости Стокс вывел ещё в 1851 году.

Он получил выражение, описывающее действие силы трения (лобового сопротивления) на круглый объект, движущийся в вязкой жидкости с небольшим числом Рейнольдса.

Чтобы понять, как определять вязкость жидкости методом Стокса необходимо узнать теоретическое описание процесса, вывод формулы и сам описание самого метода.

Всё это и конкретные методы описаны далее в статье.

Содержание статьи

Что такое вязкость

Сама по себе вязкость это свойство жидкости сопротивляться сдвигу слоев. Такой сдвиг выражается в том, что при относительном перемещении слоёв жидкости тот слой, что движется медленнее тормозит слой, который движется быстрее и наоборот.

Вязкость проявляется в наличии между молекулами жидкости сил притяжения, которые пытаются сдерживать движение слоев при перемещении одной части жидкости относительно другой.

По природе все жидкости являются вязкими, потому что между молекулами существуют силы притяжения и отталкивания. Если один слой жидкости вывести из равновесия и сдвигать его относительно другого с некоторой скоростью, то силы взаимного притяжения молекул будут пытаться тормозить это движение.

Движение тела в жидкой среде

Когда твердое тело попадает в жидкость, оно сталкивается с некоторым сопротивлением. Происхождение сил сопротивления жидкости в этом случае может быть объяснено двумя разными механизмами.

Если скорость движения твердого тела маленькая и за ним не образовывается завихрений, то силы сопротивления жидкости характеризуются только вязкостью.

В таком случае слои жидкости, которые прилегают к этому твердому телу, движутся вместе с ним. Но слои жидкости, граничащие с первыми слоями, тоже приходят в движения из-за сил молекулярного притяжения (сцепления).

Таким образом образуются силы, которые затормаживают относительное движение твердого тела в жидкости.

Завихрения вокруг твердого тела образуются из-за различия скоростей движения жидкости перед телом и за ним. При этом давление в стационарном потоке жидкости изменяется таким образом, что в области вихрей оно существенном меньше.

Разность давлений в областях перед твердым телом и за ним создает противоположную по направлению движения силу лобового сопротивления жидкости. Эта сила тормозит движение твердого тела.

Сила сопротивления

В случае, когда движение твердого тела в жидкости происходит без образования вихрей, т.е. медленно, сила сопротивления образуется по первому из двух описанных механизмов.

Для тел круглой формы, согласно формуле Стокса, сила сопротивления будет равна:

где μ – вязкость жидкости;
r – радиус шарика;
υ – скорость равномерного движения шарика.

Условие использования формулы

Существует несколько ограничений для применения формулы Стокса.
1. вязкая среда не ограничена стенками и находится в покое
2. скольжений на границах с твердым телом нет
3. движение жидкости ламинарное
4. радиус круглого тела намного больше, чем длина среднего пробега молекул жидкой среды

Формула вязкости

Рассмотрим конкретный случай, когда на шар, движущийся в жидкости действуют три силы:
F_T – сила тяжести;
F_A – сила Архимеда (выталкивающая сила);
T_C – сила лобового сопротивления.

Для круглого шарика сила тяжести будет:

где r –радиус шара;
ρ – плотность шара;
ρ₀ – плотность жидкости;
g – ускорение свободного падения;
υ – скорость равномерного движения шарика;
μ – вязкость жидкости.

В жидкости выталкивающая сила и сила тяжести постоянны. Сила лобового сопротивления пропорциональна скорости движения шарика и на первых этапах она существенно меньше силы тяжести.

При дальнейшем движении шарика наступает момент, когда все три силы уравновешиваются и тогда:

или подставляя формулы

таким образом, определение коэффициента вязкости жидкости методом Стокса сводится к формуле

Определение вязкости методом Стокса

Для того чтобы определить вязкость методом Стокса используют высокий сосуд цилиндрической формы.

На сосуд наносят метки А и В. Такие метки располагаются на заведомо известном расстоянии l друг от друга.

Затем в сосуд наливают исследуемую жидкость выше верхней метки А на 4 – 5 сантиметров. Это необходимо для того, чтобы во время прохождения шариком первой метки его скорость можно было считать установившейся.

Далее шарик бросают в сосуд и секундомером определяют время за которое он проход расстояние от метки А до метки В.

Учитывая, что скорость это отношения длины пути ко времени, т.е.:

и заменяя радиус шарика его диаметром d и определяет коэффициент вязкости жидкости методом стокса

Указанная выше формула применимо в тех случаях, когда шар падает в безграничной среде. Если он падает вдоль оси трубки диаметром R0 (как в этом случае) необходимо ввести поправки на радиус сосуда.

При падении шара радиусом r в трубе радиусом R₀ и высотой h формула будет выглядеть

Исходя из всего вышесказанного получаем, что определение вязкости жидкости методом Стокса требует значения таких параметров, как:
плотность материала шарика;
плотность жидкости;
радиус шарика;
радиус сосуда;
скорость движения шарика.

Видео про методы определения вязкости

Вязкость – это важная характеристика жидкой среды. Её необходимо учитывать при перекачке жидкостей и газов по трубопроводам, смазке машин и механизмов, разливке расплавленных металлов.

Для определения вязкости используют специальные приборы вискозиметры и специальные методы определения. Каждый из методов определения вязкости характеризуется своим набором условий применения.

Но независимо от метода общими остаются:
1. результат измерение не должен зависеть от линейных размеров вискозиметра.
2. не должно быть пристеночного скольжения жидкости.
3. поток жидкости в используемом вискозиметре должен быть ламинарным.

Источник

Формула Стокса

Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса.

Содержание

Общая формулировка

Пусть на ориентируемом многообразии M размерности n заданы ориентируемое p-мерное подмногообразие σ и дифференциальная форма ω степени p−1 класса C 1 (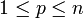). Тогда если граница подмногообразия ∂σ положительно ориентирована, то

Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия M.

Частные случаи

Формула Ньютона — Лейбница

Пусть дана кривая l, соединяющая две точки a и b (одномерная цепь) в многообразии произвольной размерности. Форма ω нулевой степени класса C 1 — это дифференцируемая функция f. Формула Стокса тогда записывается в виде

Формула Грина

Пусть M — плоскость, а D — некоторая её ограниченная область с кусочно-гладкой жордановой границей. Форма первой степени, записанная в координатах x и y — это выражение 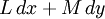, и для интеграла этой формы по границе области D верно

Формула Кельвина — Стокса

Пусть Σ — кусочно-гладкая поверхность (p = 2) в трёхмерном евклидовом пространстве (n = 3), F — дифференцируемое векторное поле. Тогда циркуляция векторного поля вдоль замкнутого контура ∂Σ равна потоку ротора (вихря) поля через поверхность Σ, ограниченную контуром:

или в координатной записи

Формула Остроградского

Пусть теперь ∂V — кусочно-гладкая гиперповерхность (p = n−1), ограничивающая некоторую область V в n-мерном пространстве. Тогда интеграл дивергенции поля по области равен потоку поля через границу области ∂V:

Что эквивалентно записи:

Литература

См. также

Полезное

Смотреть что такое «Формула Стокса» в других словарях:

ФОРМУЛА СТОКСА — формула скорости оседания частицы в жидкости: где v скорость оседания, g ускорение силы тяжести, r радиус частицы, ρ плотность вещества частицы, ρ плотность жидкости, μ коэф. вязкости жидкости. Коэф. К зависит от формы частицы и… … Геологическая энциклопедия

формула Стокса — Stokso formulė statusas T sritis fizika atitikmenys: angl. Stokes formula vok. Stokessche Formel, f rus. формула Стокса, f pranc. formule de Stokes, f … Fizikos terminų žodynas

Формула Стокса-Эйнштейна — В физике (главным образом в молекулярно кинетической теории) соотношением Эйнштейна (также называемое соотношением Эйнштейна Смолуховского) называется выражение, связывающее подвижность молекулы (молекулярный параметр) с коэффициентом диффузии и… … Википедия

Формула конечных приращений — У этого термина существуют и другие значения, см. Теорема Лагранжа. Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что если функция непрерывна на отрезке и … Википедия

Формула Гаусса—Остроградского — Формула Остроградского математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью: то есть интеграл от дивергенции векторного… … Википедия

Формула Гаусса-Остроградского — Теорема Остроградского Гаусса утверждение интегрального исчисления функций многих переменных, устанавливающее связь между n кратным интегралом по области и (n − 1) кратным интегралом по её границе. Пусть V = (v1,v2. vn) есть векторное поле… … Википедия

Стокса формула — сопротивления сферы формула, определяющая силу сопротивления X сферы диаметра d, движущейся в покоящейся вязкой несжимаемой жидкости с постоянной скоростью V( ) при малых Рейнольдса числах Re Энциклопедия техники

СТОКСА ТЕОРЕМА — обобщение Стокса формулы, утверждениео равенстве интеграла от внеш. дифференциала dw дифференциальной формы поориентированному компактному многообразию М интегралу от самой формыпо ориентированному (согласованно с ориентацией многообразия М )краю … Физическая энциклопедия

Источник

Формула Стокса

Формула Стокса для простой гладкой поверхности.

Пусть в ориентированном евклидовом пространстве задана простая поверхность \(\Sigma\) уравнением
$$
\boldsymbol = \boldsymbol(u, v),\ (u, v) \in \Omega \subset \boldsymbol^<2>.\label
$$
Здесь \(\Omega\) — замкнутая область, граница которой есть положительно ориентированный гладкий (или кусочно гладкий) контур (при обходе границы \(\partial\Omega\) область \(\Omega\) остается слева). Пусть \(\partial\Omega\) задается уравнениями
$$
u = u(t),\ v = v(t),\ \alpha \leq t \leq \beta.\label
$$
Образ кривой \(\partial\Omega\) при отображении \eqref мы назвали положительно ориентированным краем поверхности \(\Sigma\) и обозначили \(\partial\Sigma\).

Напомним, что ориентация поверхности \(\Sigma\), создаваемая полем нормалей \(\boldsymbol = [\boldsymbol_, \boldsymbol_]\), называется согласованной с положительной ориентацией края. Было показано, что такое согласование совпадает с известным правилом правого винта.

Итак, формула Стокса доказана для простой гладкой поверхности, натянутой на кусочно гладкий контур. \(\bullet\)

Формула Стокса для кусочно гладкой поверхности.

Разрежем кусочно гладкую поверхность на конечное число гладких кусков и запишем формулу Стокса для каждого куска. Если эти формулы сложить, то криволинейные интегралы по разрезам взаимно уничтожатся, так как разрезы входят в ориентированные границы кусков с противоположными ориентациями. Останется только криволинейный интеграл по краю поверхности \(\partial \Sigma\). Сумма потоков через куски даст, в силу аддитивности поверхностного интеграла, поток через всю поверхность \(\Sigma\), следовательно, формула Стокса справедлива и для кусочно гладкой поверхности.

Инвариантность ротора в ориентированном евклидовом пространстве.

При изменении ориентации пространства на противоположную нормаль к площадке и направление обхода контура \(\partial C_<\varepsilon>\) уже нужно согласовывать по правилу левого винта, и вместо формулы \eqref мы получим формулу со знаком минус. Таким образом, при изменении ориентации пространства вектор \(\operatorname\boldsymbol\) меняет знак.

Потенциальные векторные поля.

Условимся называть область \(G\) поверхностно односвязной, если на любой простой кусочно гладкий контур \(\Gamma \subset G\) можно натянуть кусочно гладкую поверхность \(\Sigma \subset G\). Например, пространство, из которого удалена одна точка, — поверхностно односвязная область, но то же пространство, из которого удалена целая прямая, не является поверхностно односвязной областью.

Как и в плоском случае, индукцией по числу звеньев ломаной теперь можно доказать, что \(\int\limits_ (\boldsymbol, d\boldsymbol) = 0\) по любой ломаной \(L\) (не обязательно простой). В силу теоремы 2 существует потенциал \(U(M)\). \(\bullet\)

Формула Стокса в некоторых случаях может упростить вычисление криволинейного интеграла.

Вычислить криволинейный интеграл
$$
J = \int\limits_<\Gamma_> (x^<2>-yz)\ dx + (y^<2>-xz)\ dy + (z^<2>-xy)\ dz,\nonumber
$$
взятый по отрезку винтовой линии (рис. 57.1) \(x = a \cos t\), \(y = a \sin t\), \(z = \displaystyle\frac<2\pi>\) от точки \(A(a, 0, 0)\) до точки \(B(a, 0, h)\).

Рис. 57.1

Таким образом,
$$
J = \int\limits_<\Gamma_> (\boldsymbol, d\boldsymbol) = \int\limits_<\Gamma’_> (\boldsymbol, d\boldsymbol) = \frac><3>.\ \blacktriangle\nonumber
$$

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Формула стокса что описывает

Математическое изучение движения тел в вязкой жидкости сопряжено со столь большими трудностями, что до сих пор такому изучению оказались доступными только предельные случаи, а именно, случай очень большой вязкости, т.е. очень малого числа Рейнольдса, и случай очень малой вязкости, т.е. очень большого числа Рейнольдса.

Если в потоке преобладают силы вязкости, что имеет место, с одной стороны, в очень вязких жидкостях (например, в моторном масле), а с другой стороны, также в обычных жидкостях при весьма малых размерах, определяющих движение, то можно пренебречь силами инерции по сравнению с силами вязкости и считать, что перепад давления и силы трения, приложенные к любой части жидкости, уравновешивают друг друга. Согласно сказанному в § 2, в геометрически подобных потоках силы трения, отнесенные к единице объема, пропорциональны Так как силы давления уравновешиваются с силами трения, то и они должны быть пропорциональны Следовательно, в рассматриваемом случае геометрическое подобие влечет за собой всегда и механическое подобие. Так как сравниваемые объемы относятся как 13, то полные силы сопротивления относятся как произведения

Для некоторых тел простой формы удалось произвести расчет потока и определить сопротивление при движении тела. Наиболее известным является решение Стокса для движения шара. Для величины сопротивления Стоке получил формулу

где а есть радиус шара, скорость его движения. Эта формула, называемая формулой Стокса, имеет важное значение для расчета падения маленьких капель. Так как в этом случае сопротивление следует принять равным весу капли за вычетом поддерживающей силы, то мы можем написать:

где есть плотность падающей капли, а плотность окружающей среды. Отсюда мы получаем скорость падения:

Эта формула применима только для таких движений, при которых число Рейнольдса мало по сравнению с единицей. Для падения водяных капель в воздухе формула (11) принимает вид:

причем а следует брать в сантиметрах. Из условия, что получается, что формула (11) верна только для капель, радиус которых меньше Из таких капель состоит туман.

Движения жидкости, при которых число Рейнольдса меньше единицы, называются ползущими течениями.

При движениях с очень большими числами Рейнольдса влияние трения делается совершенно ничтожным. Такие движения совпадали бы с движениями жидкости без трения, рассмотренными в §4-12 гл. II, если бы не было условия прилипания к стенкам, которому жидкость, лишенная трения, не может удовлетворять. Более детальное исследование показывает, что жидкость, обладающая малым трением, при движениях с большими числами Рейнольдса ведет себя вдали от стенок совершенно так же, как жидкость, лишенная трения; но около стенок она образует вследствие трения тонкий пограничный слой, в котором скорость изменяется от значения, соответствующего движению без трения, до значения, соответствующего условию прилипания. Пограничный слой тем тоньше, чем меньше вязкость. Так как внутри пограничного слоя в направлении, перпендикулярном к движению, скорость изменяется довольно быстро, то даже при очень малой вязкости здесь получаются такие силы трения, которые сравнимы с силами инерции и поэтому не могут быть отброшены, как вдали от стенок, где они ничтожно малы по сравнению с силами инерции.

Рис. 92. Распределение скоростей вблизи стенки

На рис. 92 показано распределение скоростей в пограничном слое. Если толщина пограничного слоя представляет собой величину порядка а размер тела в направлении течения — величину порядка I, то сила трения на единицу объема, равная, согласно сказанному в конце § 1, (направление у нормально к поверхности тела), будет иметь порядок а сила инерции на единицу объема, как и раньше, — порядок Так как в пограничном слое обе эти силы представляют собой величины

одного и того же порядка, то величины и пропорциональны друг другу, т. е.

означает «пропорционально»), откуда получается формула:

дающая оценку для толщины пограничного слоя.

Рис. 93. Течение вдоль пластинки

Этот же результат можно получить, применяя теорему о количестве движения к потоку вдоль плоской пластинки. Пусть пластинка имеет длину I и ширину 6; скорость течения пусть равна наконец, толщина пограничного слоя пусть приближенно равна (рис. 93). Тогда масса, входящая за одну секунду в пограничный слой, будет пропорциональна величине Эта масса, вступающая в пограничный слой со скоростью теряет здесь некоторую долю своей скорости, что приводит к соответствующей потере количества движения, которая будет пропорциональна величине Изменение количества движения должно быть равно силе, действующей на жидкость вследствие трения около стенки. Эта сила, согласно равенству (1), пропорциональна , следовательно,

откуда по-прежнему получаем:

Таким образом, отношение является функцией только числа Рейнольдса. Такая зависимость имеет место для всех пограничных слоев с установившимся движением.

В формулу (12) можно ввести время которое требуется отдельным частицам жидкости для того, чтобы пройти вдоль тела. Для частиц, двигающихся не слишком близко от поверхности тела, этот промежуток времени пропорционален поэтому формулу (12) можно переписать в следующем виде:

Формулу (13) можно применять также к движениям, которые только что начались из состояния покоя. В этом случае из нее следует, что толщина пограничного слоя возрастает в первый период движения пропорционально корню квадратному из времени.

Итак, всякое тело, движущееся в жидкости, обладающей небольшим трением, увлекает за собой тонкий слой жидкости. Такой же тонкий слой образуется и при движении жидкости в коротком канале около его стенок, но теперь этот слой отстает от общего потока жидкости. В длинных каналах пограничный слой постепенно, по мере удаления от входа в канал, увеличивается в толщине [согласно формуле (12) пропорционально корню квадратному из расстояния от входа] и в конце концов заполняет весь просвет канала. Это означает, что в длинных каналах влияние трения распространяется на все поперечное сечение. Такое увеличение толщины пограничного слоя во многих случаях происходит значительно быстрее, чем это следует из формулы (12); причиной этого является процесс перемешивания жидкости, называемый турбулентностью (см. § 4).

Касательные напряжения, возникающие на стенке при ее обтекании (рис. 92), складываясь по всей поверхности стенки, дают сопротивление трения. Для случая пластинки, обтекаемой жидкостью с двух сторон (рис. 93), легко получить приближенную оценку величины этого сопротивления. В самом деле, касательное напряжение равно

следовательно, имеет место пропорциональность

или, на основании формулы (12),

Если ширина пластинки равна то полная площадь соприкосновения с потоком будет Умножая эту площадь на мы получим искомое сопротивление:

Подробнее о сопротивлении пластинок будет сказано в §5 (стр. 180).

В существовании пограничного слоя можно убедиться при помощи следующего простого опыта. Поместим в не слишком быстрый поток воды какое-нибудь тело (пластинку, цилиндр, шар и т. п.) и подведем через заостренную стеклянную трубочку немного окрашенной жидкости к какому-нибудь месту обтекаемого тела. Убрав трубочку, мы увидим, что около поверхности тела еще долгое время остается тонкий окрашенный слой жидкости. Очевидно, что этот слой возникает вследствие прилипания частиц окрашенной жидкости к поверхности тела.

Математическое дополнение. Движение жидкости в пограничном слое может быть исследовано при помощи точных математических приемов. Как уже было сказано, в жидкости с исчезающе малой вязкостью пограничный слой получается очень тонким. Поэтому вполне допустимо внутри пограничного слоя пренебрегать разностью давлений в различных точках нормалей к стенке. В противоположность этому разности скоростей в отдельных точках нормалей весьма значительны, так как переход от скорости слоя, прилипающего к стенке, к скорости потока за пределами пограничного слоя совершается на очень коротком отрезке. Ввиду этого в выражении (7) для силы трения, отнесенной к единице объема, члены будут значительно меньше члена следовательно, могут быть отброшены (мы предполагаем, что ось х проведена в направлении потока, а ось у — в направлении нормали).

Для двухмерного потока можно пренебречь также кривизной пограничного слоя и поэтому считать, что координата х совпадает с длиной дуги линии

тока вдоль стенки. В таком случае для движения жидкости в пограничном слое получается следующая система диференциальных уравнений:

причем давление следует рассматривать как функцию от определяемую внешним потоком, т. е. потоком, лежащим вне пограничного слоя. На стенке имеют место граничные условия:

Кроме того, на стенке

как это следует из уравнения (15) после подстановки в него значений Решение этой системы уравнений может быть получено путем разложения в ряд. Для случая пластинки коэффициент пропорциональности в формуле (12) получается равным поэтому приближенно можно положить, что

Источник