как найти жорданову нормальную форму матрицы

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Жорданова нормальная форма

Жорданова нормальная форма над полем комплексных чисел

Общая схема

Аннулирующий полином

Теорема 5. Минимальный аннулирующий полином оператора является делителем его характеристического полинома. Два минимальных аннулирующих полинома оператора различаются, разве лишь, постоянным множителем.

Следствиями теорем 4 и 5 является следующий результат.

Корневое подпространство

Рассмотрим теперь пример, разобранный в ☞ ПУНКТЕ.

Пример 3. Найти корневые векторы матрицы

Доказательство. Следствие теоремы 2. ♦

Алгоритм построения базиса корневого подпространства

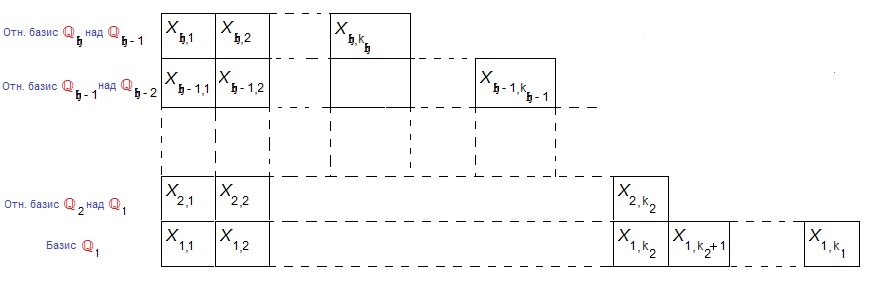
Для визуализации последующего алгоритма построения канонического базиса удобно представить результаты этого этапа в виде схемы:

Мы наблюдаем разноэтажное здание, число квартир на каждом этаже которого не превосходит числа квартир на предыдущем. В ходе дальнейшего алгоритма, часть «жильцов» останется на месте, а часть может быть замещена другими.

4. Продолжаем процесс…

Структура соответствующего канонического базиса

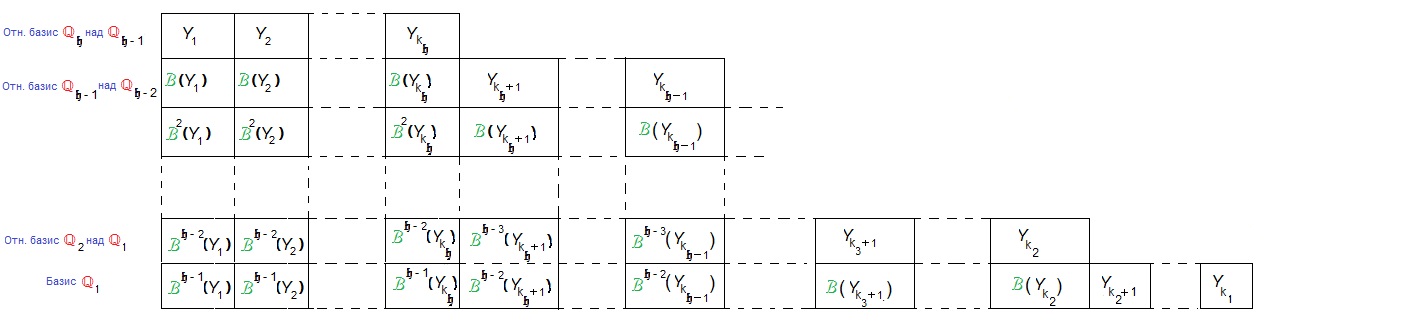
В каноническом базисе корневые векторы, соответствующие указанной последовательности клеток, следует упорядочить по следующему правилу:

Объяснение необходимости перестановки векторов канонического базиса — почему они нумеруются по правилу «сверху вниз», а не поэтажно — дается в следующем ПУНКТЕ.

Пример 3 (окончание). Построить ЖНФ и канонический базис пространства для оператора из примера 3.

Циклическое подпространство

Построить ЖНФ и канонический базис для оператора из примера 2.

Жорданова нормальная форма над полем вещественных чисел

Источник

Жорданова нормальная форма матриц

Вот тут уже пошла Высшая Алгебра. Как студент Мех-Мата я могу сказать, что это чуть ли не самая важная теорема (о жордановой нормальной форме) в годовом курсе линейной алгебры. Сегодня для меня важно вспомнить алгоритм нахождения жордановой нормальной формы (далее ЖНФ) для матриц. Этот интерес не случаен, а связан он с тем, что скоро мне, как и всему четвёртому курсу Мех-Мата, предстоит пройти письменный государственный экзамен. Даже если у вас не такая весомая мотивация, то всё равно предлагаю остаться и посмотреть, что происходит, поверьте, алгебра — это интересно! Давайте начинать)

Всё объяснять сам я не буду по двум причинам. Лень, во-первых) Во-вторых, возможно у меня не хватит компетентности. Но взамен я предлагаю вам обращаться вместе со мной к другим уважаемым алгебраистам и перенимать их опыт и знания. А я, подобно барду, буду управлять сюжетом этой баллады.

Для начала нам нужно понять, что такое ЖНФ, из чего она состоит, и зачем она, вообще, нужна. Сходим на пару ВШЭ и узнаем.

Здесь нам Ирина Кузьмина рассказала теорему Фробениуса-Перрона, и мы должны понять, что не каждая квадратная матрица может быть записана в диагональном виде…

Т.е. когда некоторые из собственных значений спектра матриц могут совпадать. Напомню, что спектром называется множество всех собственных чисел матрицы.

Ирина ответила на главный вопрос — зачем нужна ЖНФ. Ответ: чтобы брать функции от матриц. Если мы хотим найти sin(A), cos(A), exp(A), A², A^(sqrt(2)) и др., то нам может помочь ЖНФ.

Ещё важно понять, что ЖНФ может состоять из нескольких жордановых клеток (в том числе и одной), где каждая из них будет отвечать за своё собственное число λ (греческая буква «лямбда»). Оно как раз будет располагаться по диагонали, а выше диагонали будут идти единички. Если ЖК (жорданова клетка) у нас будет размера 1х1, то тогда это будет просто λ. Все остальные элементы ЖК равны нулю. В общем виде выглядит ЖК вот так:

Для примера рассмотрим такую жорданову матрицу, которая состоит из трёх ЖК. Спектр матрицы будет содержать числа 2, 0, 3. Третья ЖК состоит только из λ = 3.

В общем виде, если мы найдём ЖНФ, то она будет выглядеть так:

Теперь пойдём по пути теории и ответим на вопрос, как так вышло, что ЖНФ существует. Для этого заглянем на мини-лекцию Алексея Савватеева, который нам расскажет как же строить жорданов базис, векторы в котором можно собрать, и получить матрицу перехода к ЖНФ.

Это непростая теория, так что приготовьтесь к таким терминам, как векторы, ядро линейного оператора, инвариантное подпространство… Всё это нужно, если вы хотите понять, как и что получилось, а также почему это, вообще, можно делать. Но если вы не хотите углубляться в теорию, то нужно найти какой-то простой способ нахождения ЖНФ. Ведь должны же быть другие способы нахождения этого важного математического объекта. Существуют ли другие способы. Ответ: да, существует множество способов. Более того, мы даже можем угадать ЖНФ, а потом доказать, что это именно она, но это уже высший пилотаж. Что же делать нам, простым смертным? Нужен понятный и относительно простой алгоритм.

Однако если вы на этом этапе не до конца поняли, что значит «найти жорданов базис», что такое ЖНФ, как это всё работает, и зачем мы делаем то, что делаем, то предлагаю вам ознакомиться с суперподробным видео Екатерины Пелипенко (рекомендую смотреть на скорости 1,5).

Кстати, Екатерина рассказывает про миноры (определители меньшей размерности, чем исходная матрица А), а также находит НОД (наибольший общий делитель) полиномов второй степени, полученных как миноры характеристической матрицы для А. Ещё попутно можно вспомнить, что такое ФСР (фундаментальная система решений). Для кого-то это может быть полезным.

PPS: Евгения в своём видео также находит трансформирующую матрицу (тоже самое, что и матрица перехода). Она обозначила её за U, но обычно (как было на моих лекциях) она обозначается как T (transition matrix). Принципиально это ничего не меняет.

3PS: Если вы до конца посмотрели видео Евгении и захотели сделать проверку, то выкладываю её, дабы не тратить ваше время на перемножение матриц.

При просмотре видео вы могли заметить, что Евгения решает систему из 9 линейных уравнений. Это может показаться сложноватым, но не пугайтесь. Все действия просты, нужно лишь сконцентрироваться! Поэтому алгебра и читается на первом курсе вуза, а не в школе.

Я хотел бы рассказать про ещё один способ нахождения ЖНФ через ниль-слои. Хорошего и подробного видео, к сожалению, мне найти не удалось. В такой ситуации я могу сделать ссылку на очень хорошую методичку В. А. Чуркина, кандидата физико-математических наук. Здесь подробно изложено нахождение ЖНФ данным методом. Кроме того, данное пособие стоит прочесть тем, кто хочет глубже погрузиться в курс линейной алгебры.

Ладно, для закрепления всего этого материала предлагаю посмотреть ещё несколько примеров на популярном сайте Math Help Planet. Надеюсь, что всё это было достаточно подробно.

Я старался сделать статью математически формальной, насколько это было возможно, но и в то же время доступной для широкого круга читателей нашей группы ВК. Надеюсь, вы приятно и продуктивно потратили время. Сегодня мы затронули тему из линейной алгебры, вы поняли как и зачем искать ЖНФ, а я имел удовольствие написать данную статью. Если остались вопросы, вы можете задавать их в комментариях.

Желаю вам успехов в дальнейшем изучении математики, всего вам наилучшего!

5PS: Статья была отредактирована, добавлены ссылки к ключевым определениям, которые лучше позволяют понять материал.

Источник

СОДЕРЖАНИЕ

Обзор

Обозначение

В некоторых учебниках есть поддиагональ ; то есть непосредственно под главной диагональю, а не на наддиагонали. Собственные значения по-прежнему находятся на главной диагонали.

Мотивация

Комплексные матрицы

где каждый блок J _i представляет собой квадратную матрицу вида

Предполагая этот результат, мы можем вывести следующие свойства:

Пример

Пример: получение нормальной формы

В этом примере показано, как вычислить нормальную форму Жордана данной матрицы.

о котором упоминается в начале статьи.

Вычисление показывает, что уравнение P −1 AP = J действительно выполняется.

Обобщенные собственные векторы

Доказательство

В противном случае, если

Уникальность

Можно показать, что жорданова нормальная форма данной матрицы A единственна с точностью до порядка жордановых клеток.

равно удвоенному количеству жордановых блоков размера k ₁ плюс количество жордановых блоков размера k ₁ −1. Общий случай аналогичен.

Реальные матрицы

и описать умножение на в комплексной плоскости. Наддиагональные блоки представляют собой единичные матрицы 2 × 2 и, следовательно, в этом представлении размерности матрицы больше, чем у комплексной жордановой формы. Полный реальный блок Джордана дается формулой λ я <\ displaystyle \ lambda _ >

Эта вещественная жорданова форма является следствием комплексной жордановой формы. Для действительной матрицы невещественные собственные векторы и обобщенные собственные векторы всегда можно выбрать для образования комплексно сопряженных пар. Взяв действительную и мнимую части (линейную комбинацию вектора и сопряженного с ним), матрица имеет такой вид относительно нового базиса.

Матрицы с записями в поле

Последствия

Можно видеть, что нормальная форма Жордана является, по сути, результатом классификации квадратных матриц, и поэтому несколько важных результатов линейной алгебры можно рассматривать как ее следствия.

Теорема о спектральном отображении

Характеристический полином

Теорема Кэли – Гамильтона

Минимальный многочлен

Инвариантные разложения подпространств

Можно также получить несколько иное разложение с помощью жордановой формы. Для заданного собственного значения λ _i размер его наибольшего соответствующего жорданова блока s _i называется индексом λ _i и обозначается ν (λ _i ). (Следовательно, степень минимального многочлена равна сумме всех индексов.) Определим подпространство Y _{i следующим} образом:

Это дает разложение

Здесь может быть интересно отметить некоторые свойства индекса ν ( λ ). В более общем смысле, для комплексного числа λ его индекс может быть определен как наименьшее неотрицательное целое число ν (λ) такое, что

Плоская (плоская) нормальная форма

Жорданова форма используется для нахождения нормальной формы матриц с точностью до сопряжения, такой что нормальные матрицы составляют алгебраическое многообразие низкой фиксированной степени в пространстве объемлющих матриц.

Множества представителей классов матричной сопряженности для жордановой нормальной формы или рациональных канонических форм в общем случае не составляют линейных или аффинных подпространств в объемных матричных пространствах.

Для алгебраически замкнутых полей она была решена Петерисом Даугулисом. Построение однозначно определенной плоской нормальной формы матрицы начинается с рассмотрения ее жордановой нормальной формы.

Матричные функции

Итерация цепочки Джордана мотивирует различные расширения к более абстрактным параметрам. Для конечных матриц получаются матричные функции; это может быть распространено на компактные операторы и голоморфное функциональное исчисление, как описано ниже.

В следующем примере показано приложение к степенной функции f ( z ) = z n :

Компактные операторы

Голоморфное функциональное исчисление

Нам потребуются следующие свойства этого функционального исчисления:

Конечномерный случай

Теорема о спектральном отображении говорит нам

имеет спектр <0>. По свойству 1 f ( T ) может быть непосредственно вычислено в жордановой форме, и, проверив, мы видим, что оператор f ( T ) e _i ( T ) является нулевой матрицей.

Поляки оператора

Точка λ называется полюсом оператора T порядка ν, если резольвентная функция R _T, определенная равенством

имеет полюс порядка ν в точке λ.

Мы покажем, что в конечномерном случае порядок собственного значения совпадает с его индексом. Результат верен и для компактных операторов.

Согласно предыдущему обсуждению функционального исчисления,

Но мы показали, что наименьшее натуральное число m такое, что

в точности индекс λ, ν (λ). Другими словами, функция R _T имеет полюс порядка ν (λ) в точке λ.

Числовой анализ

Если матрица A имеет несколько собственных значений или близка к матрице с несколькими собственными значениями, то ее жорданова нормальная форма очень чувствительна к возмущениям. Рассмотрим, например, матрицу

Если ε = 0, то нормальная форма Жордана просто

Однако при ε ≠ 0 жорданова нормальная форма имеет вид

Источник

10.2. Жорданова нормальная форма

Определение 10.5. Жордановой клеткой порядка k, относящейся к числу ₀, называется матрица порядка k, 1 ≤ k ≤ n, имеющая вид

,

на ее главной диагонали стоит одно и то же число ₀, а на параллельной ей сверху диагонали стоят единицы, все же остальные элементы равны нулю. Например: (₀), , – жордановы клетки первого, второго и третьего порядков соответственно.

Определение 10.6. Жордановой матрицей порядка n называется матрица порядка n, имеющая вид: J = . В ней вдоль главной диагонали идут жордановы клетки J₁, J₂, …, J_s некоторых порядков, не обязательно различных, и относящиеся к некоторым числам, тоже не обязательно различным. Все места вне этих клеток заняты нулями. При этом s ≥ 1, то есть одна жорданова клетка порядка n так же считается жордановой матрицей и s ≤ n.

Замечание. Говорят, что матрица J имеет нормальную жорданову форму. Диагональная матрица является частным случаем жордановой матрицы, у нее все клетки имеют порядок 1.

10.3.Приведение матрицы к жордановой (нормальной) форме

Теорема 10.3. Жорданова нормальная форма определяется для матрицы однозначно с точностью до порядка расположения жордановых клеток на главной диагонали.

Приведем матрицу A(λ) = A – λE к каноническому виду с помощью элементарных преобразований.

A – λE = .

Отличные от единицы многочлены e_n–j+1(λ), …, e_n–1(λ), e_n(λ) называют инвариантными множителями матрицы A(λ). Среди них нет многочленов равных нулю, сумма степеней всех этих многочленов равна n, и все они раскладываются на линейные множители над множеством комплексных чисел. Пусть e_n–j+1(λ) раскладывается в произведение следующих множителей: , , …, . Назовем эти множители элементарными делителями многочлена e_n–j+1(λ).

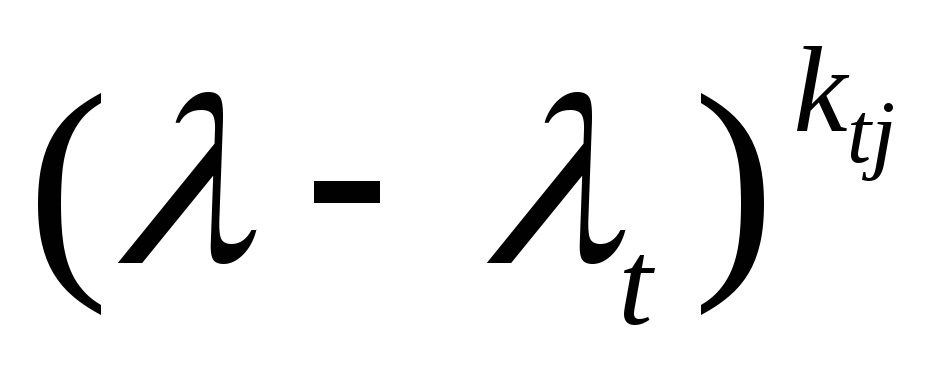
Выпишем жорданову матрицу J порядка n, составленную из жордановых клеток определяемых следующим образом: каждому элементарному делителю матрицы A(λ) ставим в соответствие жорданову клетку порядка k_ij, относящуюся к числу _i.

Пусть для некоторой матрицы порядка 9 характеристическая матрица A – λE приведена к каноническому виду.

A – λE = .

Алгоритм приведения матрицы a к жордановой форме

Составить характеристическую матрицу A – λE.

Привести эту матрицу к канонической форме с помощью элементарных преобразований.

Разложить диагональные многочлены на линейные множители.

Найти элементарные делители и по ним выписать жорданову форму матрицы A.

Для того чтобы заданная матрица была подобна диагональной матрице, необходимо и достаточно, чтобы все элементарные делители ее характеристической матрицы были первой степени.

Пример 10.4. Привести к жордановой форме матрицу A = .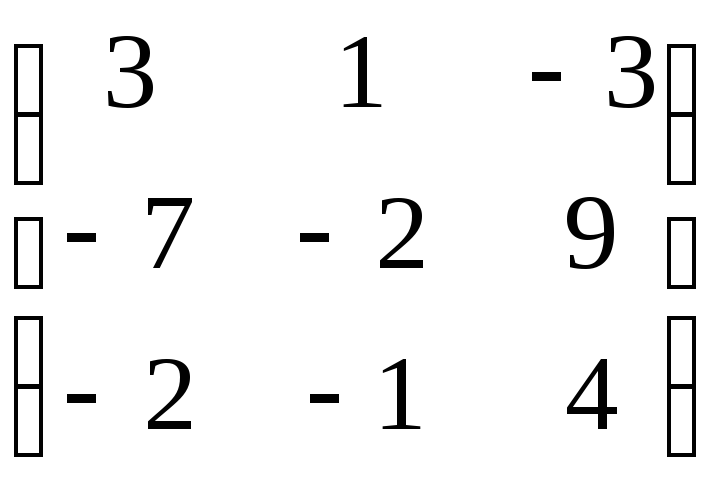

По найденным элементарным делителям выписываем жорданову форму исходной матрицы .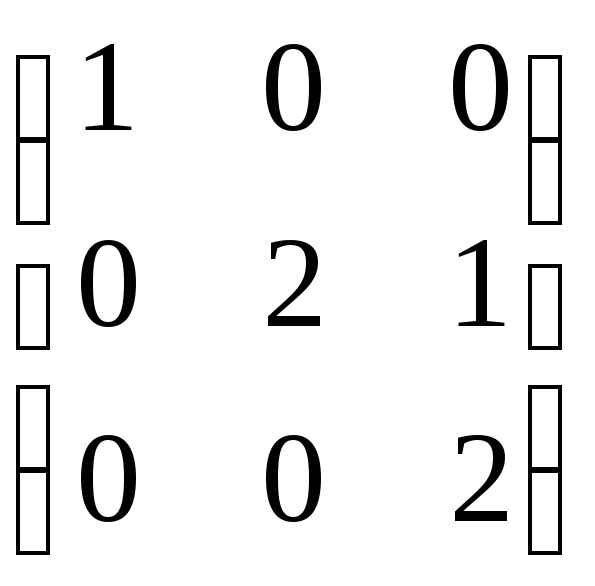

Источник

Нормальная форма Джордана

содержание

определение

Форма матрицы преобразования

Алгоритм определения сложной иорданской нормальной формы

Определение собственных значений

попарно различные собственные значения вычисляются из его нулей

Поэтому собственные значения здесь не перечислены в соответствии с их кратностью.

Определение размера жордановых блоков

вычислять. Он также дает общее количество жордановых блоков, принадлежащих этому собственному значению. а 1 <\ displaystyle a_ <1>>

Комплексная иорданская нормальная форма

Жорданова нормальная форма определяется однозначно, за исключением порядка жордановых блоков. Если все собственные значения находятся в, две матрицы с одинаковой жордановой нормальной формой похожи друг на друга. K <\ Displaystyle \ mathbb >

пример

Определение основного преобразования к комплексной иорданской нормальной форме

Теперь нужно определить базовую матрицу преобразования, которая П. ∈ грамм Л. ( п ; С. ) <\ Displaystyle P \ in <\ rm > (п; \ mathbb )>

Стандартная процедура

пример

В качестве наглядного примера рассмотрим матрицу

как указано выше. Это относится

Его нормальная жорданова форма

Начнем с первого жорданового блока размерности 2. Для этого выберите

Реальная иорданская нормальная форма

Если рассматривать вещественные матрицы, их характеристический многочлен больше не распадается полностью на линейные множители, а только на неприводимые множители, которые в этом случае всегда являются линейными или квадратичными множителями. Теперь возникает вопрос о нормальной форме, если разрешены только реальные преобразования базиса.

Мы называем количество строк (или столбцов) размером этого блока. Затем обозначают

Один из способов получить базовое преобразование заключается в следующем:

пример

Чтобы вычислить базовую матрицу преобразования, начните с первого действительного собственного значения, а затем с (первого) жорданового блока размерности 1. Выберите

Теперь перейдите к первому неприводимому множителю (комплексному собственному значению), а затем к жордановой клетке размера 4. Для этого выберите

Жорданова нормальная форма в твердых телах общего вида

Благодаря представлению в нормальной форме Вейерштрасса структура минимального многочлена сразу распознается, а характеристический многочлен может быть легко вычислен.

Приложение к системам линейных дифференциальных уравнений первого порядка с постоянными коэффициентами

y ( Икс 0 ) знак равно y 0 ∈ С. п <\ displaystyle y (x_ <0>) = y_ <0>\ in \ mathbb ^ >

Источник