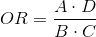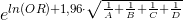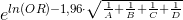как посчитать отношение шансов в spss
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
ОТНОШЕНИЕ ШАНСОВ
1. История разработки показателя отношения шансов
2. Для чего используется показатель отношения шансов?
Отношение шансов позволяет оценить связь между определенным исходом и фактором риска.
Отношение шансов позволяет сравнить группы исследуемых по частоте выявления определенного исхода. Важно, что результатом применения отношения шансов является не только определение статистической значимости связи между фактором и исходом, но и ее количественная оценка.
Отношение шансов при сравнении двух групп рассчитывается как частное от деления шансов развития исхода в основной группе к шансам развития исхода в контрольной группе. В свою очередь, шансами называют отношение числа исследуемых с наличием исхода к числу исследуемых с отсутствием исхода. Также для рассчитанного ОШ рассчитывается 95% доверительный интервал (95% ДИ).
3. Условия и ограничения применения отношения шансов
4. Как рассчитать отношение шансов?
Отношение шансов – это значение дроби, в числителе которой, находятся шансы определённого события для первой группы, а в знаменателе шансы того же события для второй группы.
Шансом является отношение числа исследуемых, имеющих определенный признак (исход или фактор), к числу исследуемых, у которых данный признак отсутствует.
Например, была отобрана группа пациентов, прооперированных по поводу панкреонекроза, число которых составило 100 человек. Через 5 лет из их числа в живых осталось 80 человек. Соответственно, шанс выжить составил 80 к 20, или 4.
Удобным способом является расчёт отношения шансов со сведением данных в таблицу 2х2:
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | A | B | A + B |
| Фактор риска отсутствует (0) | C | D | C + D |
| Всего | A + C | B + D | A + B + C + D |
Для данной таблицы отношение шансов рассчитывается по следующей формуле:
Очень важно оценить статистическую значимость выявленной связи между исходом и фактором риска. Связано это с тем, что даже при невысоких значениях отношения шансов, близких к единице, связь, тем не менее, может оказаться существенной и должна учитываться в статистических выводах. И наоборот, при больших значениях OR, показатель оказывается статистически незначимым, и, следовательно, выявленной связью можно пренебречь.
Для оценки значимости отношения шансов рассчитываются границы 95% доверительного интервала (используется абрревиатура 95% ДИ или 95% CI от англ. «confidence interval»). Формула для нахождения значения верхней границы 95% CI:
Формула для нахождения значения нижней границы 95% CI:
5. Как интерпретировать значение отношения шансов?
Дополнительно в каждом случае обязательно оценивается статистическая значимость отношения шансов исходя из значений 95% доверительного интервала.
6. Пример расчета показателя отношения шансов
1. Составим четырехпольную таблицу сопряженности:
| ВПР плода диагностирован | ВПР плода отсутствует | Всего | |
| Курящие | 50 (А) | 10 (В) | 60 |
| Некурящие | 150 (С) | 90 (D) | 240 |
| Всего | 200 | 100 | 300 |
2. Рассчитаем значение отношения шансов:
OR = (A * D) / (B * C) = (50 * 90) / (150 * 10) = 3.
Таким образом, исследование показало, что шансы встретить курящую женщину среди пациенток с диагностированным ВПР плода в 3 раза выше, чем среди женщин без признаков ВПР плода. Наблюдаемая зависимость является статистически значимой, так как 95% CI не включает 1, значения его нижней и верхней границ больше 1.
Как посчитать отношение шансов в spss
Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования зависимостей между социально-экономическими переменными. Эту задачу мы рассмотрим в рамках самой распространенной в статистических пакетах классической модели линейной регрессии.
Специфика социологических исследований состоит в том, что очень часто необходимо изучать и предсказывать социальные события. Вторая часть данной главы будет посвящена логистической регрессии, целью которой является построение моделей, предсказывающих вероятности событий.
Линейная модель связывает значения зависимой переменной Y со значениями независимых показателей X k (факторов) формулой:
Y=B 0 +B 1 X 1 +:+B p X p + e
Традиционные названия «зависимая» для Y и «независимые» для X k отражают не столько статистический смысл зависимости, сколько их содержательную интерпретацию.
Кроме того, с учетом дисперсии остатка могут быть вычислены доверительные границы значений Y (не средних, а индивидуальных!).
Это далеко не полный перечень переменных, порождаемых SPSS.
Например, в приведенном примере на достаточно больших данных можно оценить дисперсию для каждой возрастной группы и вычислить необходимую весовую переменную. Увеличение влияния возрастных групп с меньшим возрастом в данном случае вполне оправдано.
— Назначаются независимые и зависимая переменные,
— Имеется возможность отбора данных, на которых будет оценена модель (Selection). Для остальных данных могут быть оценены прогнозные значения функции регрессии, его стандартные отклонения и др.
— Задаются графики рассеяния остатков, их гистограммы (Plots)
— Назначаются сохранение переменных(Save), порождаемых регрессией.
— Если используется пошаговая регрессия, назначаются пороговые значимости для включения (PIN) и исключения (POUT) переменных (Options).
— Если обнаружена гетероскедастичность, назначается и весовая переменная.
Обычно демонстрацию модели начинают с простейшего примера, и такие примеры Вы можете найти в Руководстве по применению SPSS. Мы пойдем немного дальше и покажем, как получить полиномиальную регрессию.
REGRESSION /DEPENDENT lnv14m /METHOD=ENTER v9 v9_2
/SAVE PRED MCIN ICIN.
*регрессия с сохранением предсказанных значений и доверительных интервалов средних и индивидуальных прогнозных значений.
Таблица 5.1 показывает, что уравнение объясняет всего 4.5% дисперсии зависимой переменной (коэффициент детерминации R 2 =.045), скорректированная величина коэффициента равна 0.042, а коэффициент множественной корреляции равен 0.211. Много это или мало, трудно сказать, поскольку у нас нет подобных результатов на других данных, но то, что здесь есть взаимосвязь, можно понять, рассматривая таблицу 6.2.
Таблица 6.1. Общие характеристики уравнения
Std. Error of the Estimate
a Predictors: (Constant), V9_2, V9 Возраст
b Dependent Variable: LNV14M логарифм промедианного дохода
Результаты дисперсионного анализа уравнения регрессии показывает, что гипотеза равенства всех коэффициентов регрессии нулю должна быть отклонена.
Таблица 6.2. Дисперсионный анализ уравнения
Иллюстрированный самоучитель по SPSS 10/11
Другие меры связанности
Теперь вычислим статистику Кохрана и Мантеля-Хэнзеля.
Из полученных результатов ниже приводится только статистика Кохрана и Мантеля-Гензеля.
Test of Homogenity of the Odds Ratio (Тест на гомогенность отношения шансов). Statistics
| Statistics | Chi-Squared (Хи-квадрат) | df | Asymp. Sig. (2-sided) | |
| Conditional (Условная независимость) | Cochran (Кохран) | 44.665 | 1 | 0.000 |
| Mantel-Haenszel (Мантель-Гензель) | 43.724 | 1 | 0.000 | |
| Homogeneity (Гомогенность) | Breslow-Day (Бреслоу-Дэй) | 1.522 | 1 | 0.217 |
| Tarone (Тарой) | 1.522 | 1 | 0.217 | |
Under the conditional independence assumption, Cochran’s statistic is asymptotically distributed as a 1 df chi-squared distribution, only if the number of strata is fixed, while the Mantel-Haenszel statistic is always asymptotically distributed as a 1 df chi-squared distribution. Note that the continuity correction is removed from the Mantel-Haenszel statistic when the sum of the differences between the observed and the expected is 0. (При гипотезе условной независимости статистика Кохрана дает распределение, асимптотически приближающееся к распределению хи-квадрат с 1-ой степенью свободы, только при фиксированном количестве слоев, в то время как статистика Мантеля-Хэнзеля при той же гипотезе всегда дает такое распределение. Обратите внимание, что в статистике Мантеля-Хэнзеля опускается коррекция на непрерывность, если сумма разностей наблюдаемых и ожидаемых величин равна 0.)
Mantel-Haenszel Common Odds Ratio Estimate (Оценка общего отношения шансов Мантеля-Гензеля)
| Estimate (Оценка) | 2.503 | ||
| ln(Estimate) | 0.918 | ||
| Std. Error of (Стандартная ошибка) In(Estimate) | 0.141 | ||
| Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя) | 0.000 | ||
| Asymp. 95% Confidence Interval (Асимптотический 95% доверительный интервал) | Common Odds Ratio (Общее отношение шансов) | Lower Bound (Нижняя граница) | 1.901 |
| Upper Bound (Верхняя граница) | 3.297 | ||
| ln(Common Odds Ratio) | Lower Bound (Нижняя граница) | 0.642 | |
| Upper Bound (Верхняя граница) | 1.193 | ||
The Mantel-Haenszel common odds ratio estimate is asymptotically normally distributed under the common odds ratio of 1.000 assumption. So is the natural log of the estimate. (Оценка общего отношения шансов Мантеля-Хэнзеля при условии, что общее отношение шансов равно 1.000, имеет асимптотически нормальное распределение. То же распределение сохраняется и для натурального логарифма оценки.)
Результаты тестов Кохрана и Мантеля-Хэнзеля очень близки; в обоих случаях для весовых групп наблюдается максимально значимое отличие отношения шансов от 1 (р
СОДЕРЖАНИЕ
Определение и основные свойства
Убедительный пример в контексте предположения о редком заболевании
Определение с точки зрения групповых шансов
Определение в терминах совместной и условной вероятностей
Таким образом, отношение шансов
Симметрия
мы получили бы тот же результат
Отношение к статистической независимости
Если X и Y независимы, их совместные вероятности могут быть выражены через их предельные вероятности p x = P ( X = 1) и p y = P ( Y = 1) следующим образом
Восстановление вероятностей ячеек из отношения шансов и предельных вероятностей
Пример
Предположим, что в выборке из 100 мужчин 90 пили вино на предыдущей неделе (значит, 10 не пили), в то время как в выборке из 80 женщин только 20 пили вино за тот же период (то есть 60 не пили). Это формирует таблицу непредвиденных обстоятельств:
Отношение шансов (OR) можно напрямую рассчитать из этой таблицы как:
В качестве альтернативы, шансы мужчины, пьющего вино, составляют 90 к 10, или 9: 1, в то время как шансы женщины, пьющей вино, составляют всего 20 к 60, или 1: 3 = 0,33. Соотношение шансов, таким образом, составляет 9 / 0,33, или 27, что показывает, что мужчины гораздо чаще пьют вино, чем женщины. Подробный расчет:
Статистические выводы
Было разработано несколько подходов к статистическому выводу для отношений шансов.
Один из подходов к выводу использует приближения большой выборки к выборочному распределению логарифмического отношения шансов ( натуральный логарифм отношения шансов). Если мы используем обозначение совместной вероятности, определенное выше, логарифмическое отношение шансов популяции будет
то вероятности в совместном распределении можно оценить как
L знак равно бревно ( п ^ 11 п ^ 00 п ^ 10 п ^ 01 ) знак равно бревно ( п 11 п 00 п 10 п 01 ) <\ displaystyle > _ <00>> <<\ hat > _ <10>) <\ hat > _ <01>>> \ right) = \ log \ left ( <\ dfrac Распределение логарифмического отношения шансов приблизительно нормальное при: Стандартная ошибка для логарифмического отношения шансов приблизительно S E знак равно 1 п 11 + 1 п 10 + 1 п 01 + 1 п 00 <\ displaystyle <<\ rm Этот факт используется в двух важных ситуациях: В обеих этих настройках отношение шансов может быть рассчитано на основе выбранной выборки без смещения результатов по сравнению с тем, что было бы получено для выборки населения. Если доступен абсолютный риск в неэкспонированной группе, конверсия между ними рассчитывается следующим образом: Если предположение о редком заболевании неприменимо, отношение шансов может сильно отличаться от относительного риска и вводить в заблуждение. Рассмотрим уровень смертности пассажиров-мужчин и женщин, когда затонул Титаник. Из 462 женщин 154 умерли и 308 выжили. Из 851 мужчины 709 умерли, 142 выжили. Очевидно, что у мужчины на «Титанике» больше шансов умереть, чем у женщины, но насколько больше? Поскольку более половины пассажиров погибли, предположение о редкой болезни сильно нарушается. Чтобы вычислить отношение шансов, обратите внимание, что для женщин шансы умереть были 1: 2 (154/308). У мужчин шансы были 5 к 1 (709/142). Отношение шансов составляет 9,99 (4,99 / 0,5). У мужчин в десять раз больше шансов умереть, чем у женщин. Для женщин вероятность смерти составила 33% (154/462). Для мужчин вероятность составила 83% (709/851). Относительный риск смерти составляет 2,5 (0,83 / 0,33). Вероятность смерти мужчины в 2,5 раза выше, чем у женщины. Какое число правильно представляет, насколько опаснее было находиться на Титанике? Относительный риск имеет то преимущество, что его легче понять и лучше представить, как думают люди. В медицинской литературе отношение шансов часто путают с относительным риском. Для нестатистиков понятие отношения шансов является трудным для понимания, и оно дает более впечатляющую цифру для эффекта. Однако большинство авторов считают, что относительный риск легко понять. В одном исследовании члены национального фонда борьбы с болезнями на самом деле были в 3,5 раза чаще, чем не члены, слышали об общем лечении этого заболевания, но отношение шансов составляло 24, и в документе говорилось, что члены были более чем в 20 раз более вероятны. слышать о лечении. Исследование статей, опубликованных в двух журналах, показало, что 26% статей, в которых использовалось отношение шансов, интерпретировали его как отношение рисков. Это может отражать простой процесс, когда непонимающие авторы выбирают наиболее впечатляющую и пригодную для публикации фигуру. Но в некоторых случаях его использование может быть заведомо вводящим в заблуждение. Было высказано предположение, что отношение шансов следует представлять как меру величины эффекта только в том случае, если отношение рисков невозможно оценить напрямую. Это снова то, что называется «инвариантностью отношения шансов», и почему RR для выживания не то же самое, что RR для риска, в то время как OR имеет это симметричное свойство при анализе либо выживаемости, либо неблагоприятного риска. Опасность клинической интерпретации OR возникает, когда частота нежелательных явлений не является редкой, что приводит к преувеличению различий, когда предположение OR редкого заболевания не выполняется. С другой стороны, когда заболевание встречается редко, использование RR для выживаемости (например, RR = 0,9796 из приведенного выше примера) может клинически скрыть и скрыть важное удвоение неблагоприятного риска, связанного с лекарством или воздействием. Следующие четыре таблицы непредвиденных обстоятельств содержат наблюдаемое количество клеток, а также соответствующее отношение шансов выборки ( OR ) и отношение шансов журнала выборки ( LOR ): Следующие совместные распределения вероятностей содержат вероятности ячеек популяции, а также соответствующее отношение шансов популяции ( OR ) и логарифмическое отношение шансов популяции ( LOR ): Отношение вероятности того, что событие произойдет,к вероятности того, что оно не произойдет,P / (1 –P),называется отношением шансов. В связи с этим отношение шансов может быть записано в следующем виде: P/(1–P) = Отсюда получается, что, если модель верна, изменение x k на единицупри независимых x 1 , …, x p вызывает изменение отношения шансов в Решение такого уравнения упрощенно можно представить следующим образом Получаются агрегированные данные по переменным x, в которых для каждой группы, характеризуемой значениямиxj = Еще одна особенность состоит в том, что в реальных данных очень часто группы по xоказываются однородными поy, поэтому оценки В некоторых статистических пакетах такие группы объектов просто-напросто отбрасываются. В настоящее время в статистическом пакете для оценки коэффициентов используется метод максимального правдоподобия, лишенный этого недостатка. Тем не менее проблема, хотя и не в таком остром виде,остается: если оценки вероятности для многих групп оказываются равными0или1, оценки коэффициентов регрессии имеют слишком большую дисперсию. Поэтому, имея в качестве независимых переменных такие признаки, как душевой доход в сочетании с возрастом, их следует укрупнить по интервалам, приписав объектам средние значения интервалов. Если в обычной линейной регрессии для работы с неколичественными переменными нам приходилось подготавливать специальные индикаторные переменные, то в реализации логистической регрессии в SPSS это делается автоматически. Для этого в диалоговом окне специально предусмотрены средства, сообщающие пакету, что ту или иную переменную следует считать категориальной. При этом, чтобы не получить линейно зависимых переменных, максимальный код ее значения (или минимальный, в зависимости от задания процедуры) не перекодируется в дихотомическую (индексную) переменную. Впрочем, средства преобразования данных позволяют не учитывать любой код значения. Имеются другие способы перекодирования категориальных (неколичественных) переменных в несколько переменных, но мы будем пользоваться только указанным способом как наиболее естественным.

Роль в логистической регрессии
Нечувствительность к типу отбора проб
Использование в количественных исследованиях
Отношение к относительному риску
Замешательство и преувеличение
Обратимость и инвариантность
Оценщики отношения шансов
Отношение шансов выборки
Альтернативные оценщики
Числовые примеры
Числовой пример
Связанная статистика
6.2.1.Отношение шансов и логит


6.2.2. Решение уравнения с использованием логита




6.2.3. Неколичественные данные
6.2.4. Взаимодействие переменных