Эконометрика с чего начать

Используются и другие типы кривых:

; ; ;

; ; .

Аналитический метод выбора типа уравнения регрессии основан на изучении материальной природы связи исследуемых признаков.

Пусть, например, изучается потребность предприятия в электроэнергии y в зависимости от объема выпускаемой продукции x. Все потребление электроэнергии можно подразделить на 2 части:

— не связанное с производством продукции a;

— непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска bx;

Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида

Разделив на x, получим удельный расход электроэнергии на единицу продукции :

Это равносторонняя гипербола.

Аналогично затраты предприятия могут быть условно-переменные, изменяющиеся пропорционально изменению объема продукции (расход материала, оплата труда и др.) и условно-постоянные, не изменяющиеся с изменением объема производства (арендная плата, содержание администрации и др.). Соответствующая зависимость затрат на производство y от объема продукции x характеризуется линейной функцией.

,

а зависимость себестоимости единицы продукции zx от объема продукции – равносторонней гиперболой:

Экспериментальный метод используется при обработке информации на компьютере путем сравнения величины остаточной дисперсии , рассчитанной на разных моделях. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии факторов:

Чем меньше , тем меньше наблюдается влияние прочих факторов, тем лучше уравнение регрессии подходит к исходным данным. При обработке данных на компьютере разные математические функции перебираются в автоматическом режиме, и из них выбирается та, для которой является наименьшей.

Если примерно одинакова для нескольких функций, то на практике выбирают более простую, так как она в большей степени поддается интерпретации и требует меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной x. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений. Для рядов динамики, ограниченных по протяженности – 10, 20, 30 лет – предпочтительна модель с меньшим числом параметров при x.

Оценка параметров линейной регрессии.

Линейная регрессия сводится к нахождению уравнения вида

(или)

Первое выражение позволяет по заданным значениям фактора x рассчитать теоретические значения результативного признака, подставляя в него фактические значения фактора x. На графике теоретические значения лежат на прямой, которая представляют собой линию регрессии.

МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений от теоретических минимальна:

или

(5)

Преобразуем, получаем систему нормальных уравнений:

(6)

В этой системе n— объем выборки, суммы легко рассчитываются из исходных данных. Решаем систему относительно а и b, получаем:

(7)

. (8)

Выражение (7) можно записать в другом виде:

(9)

где ковариация признаков, дисперсия фактора x.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.

Формально a— значение y при x=0. Если x не имеет и не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать его могут привести к абсурду, особенно при a 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Сравним эти относительные изменения:

0, > 0

Иногда линейное уравнение парной регрессии записывают для отклонений от средних значений:

, (10)

где , . При этом свободный член равен нулю, что и отражено в выражении (10). Этот факт следует из геометрических соображений: уравнению регрессии отвечает та же прямая (3), но при оценке регрессии в отклонениях начало координат перемещается в точку с координатами . При этом в выражении (8) обе суммы будут равны нулю, что и повлечет равенство нулю свободного члена.

Рассмотрим в качестве примера по группе предприятий, выпускающих один вид продукции, функцию издержек

Выпуск продукции тыс. ед.()

производство, млн. руб.()

Источник

Эконометрика

Эконометрика — это наука, в которой строятся, анализируются и совершенствуются математические модели социально-экономических явлений.

Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью статистических и других математических методов и моделей. Современное определение предмета эконометрики было выработано в уставе Эконометрического общества, которое главными целями назвало использование статистики и математики для развития экономической теории. Теоретическая эконометрика рассматривает статистические свойства оценок и испытаний, в то время как прикладная эконометрика занимается применением эконометрических методов для оценки экономических теорий. Эконометрика даёт инструментарий для экономических измерений, а также методологию оценки параметров моделей микро- и макроэкономики. Кроме того, эконометрика активно используется для прогнозирования экономических процессов как в масштабах экономики в целом, так и на уровне отдельных предприятий. При этом эконометрика является частью экономической теории, наряду с макро- и микроэкономикой. wikipedia.org/wiki/Эконометрика

Основные понятия эконометрики и принципы моделирования социально-экономических систем

Поскольку экономическая практика объясняется высоким уровнем развития производительных сил, глубокой специализацией производства, ускорением темпов научно-технического прогресса, то предъявляются дополнительные требования к эффективности использования природных ресурсов и экологическим последствиям хозяйственной деятельности. Для учета вышеназванных факторов при принятии решений в народном хозяйстве широко используется эконометрика.

Что такое «модель», «моделирование» в эконометрике

Математической моделью называется система математических соотношений (уравнений, неравенств, формул, и др.), описывающих реальный объект, составляющие его характеристики и взаимосвязи между ними.

Моделирование — это изучение объектов исследования не непосредственно, а косвенным путем, с помощью анализа моделей.

Классификацию методов моделирования и моделей можно проводить по различным признакам: по сфере приложения, характеру моделируемых объектов, степени подробности моделей и т.д.

В зависимости от средств моделирования различают методы материального и идеального моделирования.

При исследовании экономических процессов и явлений, выявляются закономерные связи и отношения между ее элементами. Закономерность, будучи закономерностью массовых явлений и процессов, проявляется в статистической совокупности.

Принцип, согласно которому закономерность массового явления может проявиться только в достаточно большем числе случаев, когда совокупное действие множества случайных причин приводит к результату, уже почти не зависящему от случая, носит название закона больших чисел. Закон больших чисел отражает диалектическую связь между необходимостью и случайностью. Например, рассматривая сферу обращения в рыночных условиях, можно увидеть, что это сфера конкуренции, где, если рассматривать каждый отдельный случай, господствует случайность, в которой, следовательно, внутренний закон, прокладывающий себе дорогу через эти случайности и регулирующий их, становится видимым лишь тогда, когда они проявляются в больших массах.

На основании закона больших чисел закономерные связи между элементами экономической системы обнаруживаются в массовых явлениях с использованием идеального моделирования. При этом применяется аппарат теории вероятностей и математической статистики. Такое идеальное моделирование называют вероятностным.

Отметим, что дальнейшее развитие математического моделирования и прогнозирования пойдет по пути использования достижений экспертных систем (ЭС) — пакетов программного обеспечения, предназначенных для имитации деятельности человека (эксперта). Они позволяют делать логические выводы из знаний в конкретной предметной области и обеспечивают решение специфических задач.

Главный объект математического моделирования — социально-экономические явления и процессы производства, которые обладают свойством сохранять присущие им тенденции и закономерности в будущем. Устойчивость социально-экономических явлений обусловливается постоянством воздействия определяющих факторов в течение длительных периодов времени.

Целью математического моделирования является разработка адекватной модели объекта, которую можно использовать и для прогнозирования. Для построения такой модели используется информация о состоянии объекта в данный момент и о его прошлом состоянии

Математические модели должны удовлетворять следующим требованиям:

Классификация математических методов и моделей

Математические модели социально-экономических явлений и процессов можно классифицировать так, как показано на рис. В.1.

Модели структуры выражаются рядами и кривыми распределения. Модели структуры на основе группировок используются для изучения структуры народного хозяйства и его отраслей, для контроля за выполнением народнохозяйственных планов. Моделирование на основе группировок не связано с законами распределения и характеризует социально-экономические явления в «чистом» виде. Такие модели не позволяют делать количественные оценки, строить прогнозы, в них завуалированы тенденции развития социально-экономических явлений.

Модели структуры, выражающие сходство, строят с помощью мер близости (метрик), которые предполагают использование математического понятия расстояния (Евклидового, Хеммингова, Махаланобиса и т.д.). Меры близости позволяют выделять качественно однородные группы одновременно по большему числу признаков. Модели структуры, основанные на мерах близости (сходства), должны удовлетворять следующим условиям:

Модели структуры на основе кривых распределения характеризуют структуру социально-экономических явлений. Используя такие модели, можно сравнивать структуру социально-экономических явлений, имеющих различное происхождение, но относящихся к одному и тому же виду, и интерполировать распределение для значений, которые не были получены в результате наблюдений. Отметим, что выбор кривых распределения должен опираться на предварительный качественный анализ исследуемого явления. Кроме того, кривые распределения по возможности должны иметь более простое уравнение, и соответствующее уравнение должно содержать возможно меньшее число параметров.

Модели взаимосвязи описываются уравнениями регрессии. Построенное уравнение регрессии, проверенное на адекватность, становится статистической моделью, обладающей определенными прогнозными свойствами. Для учета всей системы сложных причинных связей и взаимосвязей результативных и факторных признаков строится регрессионная модель вида

Такая модель может быть развернута в систему регрессионных уравнений, каждое из которых будет отражать одну из зависимостей исследуемого сложного объекта.

Все признаки, входящие в регрессионную модель, можно разделить на эндогенные и экзогенные. Эндогенные (результативные) признаки — это показатели, описываемые уравнениями модели. Их значения зависят от внутренней структуры объекта. Эндогенные признаки можно получить из решения системы. Экзогенные (факторные) признаки задаются извне и не зависят от структуры модели.

Если система разрешима относительно эндогенных показателей, то регрессионная модель сложного вида записывается в виде системы структурных уравнений:

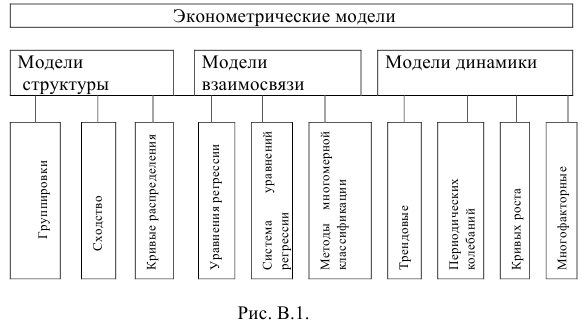
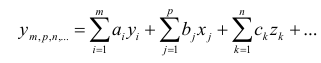
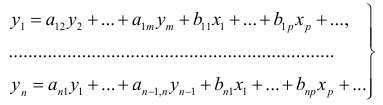
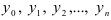Модели динамики описываются функциями времени на основе трендовых моделей. Параметры трендовых моделей определяются методом наименьших квадратов. При этом предполагается, что тенденция, описываемая исходным динамическим рядом, остается неизменной. Динамический ряд образует числовая последовательность наблюдений , характеризующих изменение экономического явления во времени, т.е. зарегистрированных в последовательные моменты времени 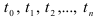. Единственным независимым признаком в трендовых моделях является время .

Многофакторное моделирование динамики осуществляется на основе связных рядов. Модель может быть выражена многофакторным уравнением регрессии, в котором время является дополнительным факторным признаком.

Для выявления главных черт моделей рассмотрим пример.

Пример: (предложение и спрос на конкурентном рынке).

Разделение труда в рыночных условиях сопровождается многочисленными обменами, благодаря которым производимые ценности распределяются по различным каналам. Каждый обмен — это результат свободного соглашения между продавцом и покупателем товара по согласованной между ними цене.

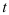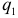Пусть — запрашиваемые, 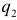— предложенные количества какого-либо продукта в некоторый день на рынке, а 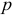— цена, по которой заключаются сделки. Ясно, что и 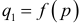зависят от цены , так как участники рынка, совершающие сделки, решают не покупать или не продавать, если цена их не устраивает. Следовательно, и 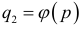функции спроса и предложения, которые определяют соответственно 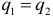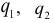и , если задана цена . Равновесие на рынке определяется равенством .

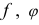Итак, формально модель рынка устанавливает между тремя неотрицательными числовыми переменными и две зависимости: и где — заданные функции. Статистическая модель в случае равновесия имеет вид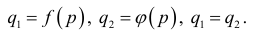

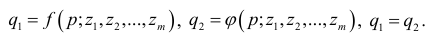
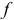Эта модель отражает лишь зависимость предложения и спроса от цены данного продукта, хотя в действительности они в различной степени зависят от множества цен и системы снабжения в рассматриваемой экономической системе. Поэтому модель вида (В.1) можно записать так:

Здесь функции и 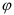зависят от стольких переменных, сколько их требуется для достаточно адекватного представления факторов, влияющих на предложение и спрос.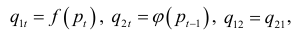

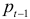Модели (В.1) и (В.2) предполагают мгновенную адаптацию предложения и спроса при изменениях цен в связи с тем, что в них не учитывается влияние времени. Если же предложение и спрос зависят от времени года, то предпочтительнее следующая модель:

в которой цена , года 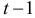определяет предложение года .

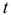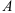Если цена равна , то точка на кривой предложения 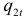определяет , равное 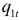. Соответствующая точка 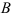на кривой спроса 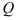определяет .

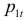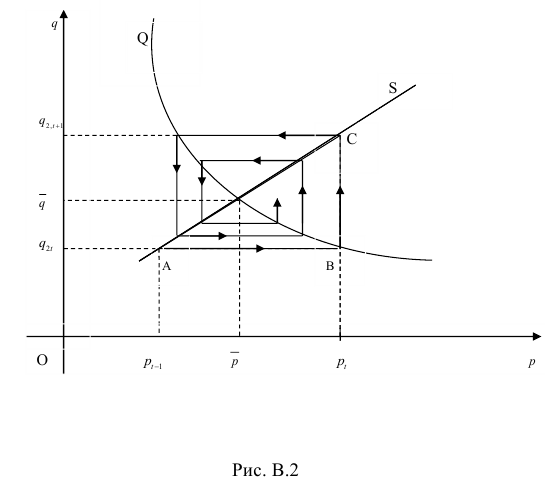
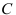Точка на кривой предложения 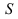определяет 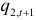и т.д. Двигаясь по ломаной спирали, находим цену, спрос и предложение. Ясно, что в зависимости от вида кривых 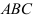и ломаная линия … имеющая вид паутины, может сходиться к точке равновесия модели (В.З) или нет.

Рассмотренная модель взята из экономической теории и достаточно хорошо иллюстрирует характерные общие формы модели. Из этой модели видно, какие логические проблемы возникают при изучении фактических данных.

Этапы построения математических моделей для эконометрики

Первый этап состоит в проведении качественного анализа экономической системы: вскрытие и обоснование причинно-следственных связей, оценка основных составляющих экономической системы, выявление объективно существующих причинно-следственных связей между факторами, установление существенных черт, свойств, отношений, закономерностей развития моделируемых явлений, которые должны быть абстрагированы от второстепенных, несущественных случайных связей и факторов. Экономические показатели, выступающие в роли результативных признаков, выбирают исходя из цели исследования. Независимые переменные (признаки-факторы) выбирают в процессе последовательного уточнения первоначальной гипотезы. В этом процессе выделяются следующие этапы: 1) формирование первичной гипотезы о наборе независимых переменных; 2) экспертная оценка сформированного набора; 3) анализ структурных связей; 4) сужение круга и отбор существенных для моделирования переменных. Затем качественная информация переводится на язык математики, т.е. формируется статистическая совокупность данных, представляющих собой зафиксированные результаты измерения признаков, выражающих свойства исследуемой экономической системы.

На втором этапе выбирается и формируется тип модели. Выбор модели основывается на обобщении результатов первого этапа. Формирование ее заключается в описании зависимостей в символах и знаках, в переводе качественной информации на язык математики. Модель получают в виде группировки, ряда распределения, уравнения, системы уравнений и т.д. Таким образом, второй, собственно моделирующий, этап включает непосредственный вывод общего вида модельных соотношений, связывающих между собой факторные и результативные признаки. Этот вывод опирается на принятие и частично экспериментально подтвержденные исходные допущения. На данном этапе подтверждается лишь структура модели, ее символьная аналитическая запись, в которой наряду с известными числовыми значениями присутствуют неизвестные параметры, модели, подлежащие статистическому оцениванию. Этот этап называется этапом спецификации модели.

На четвертом этапе (этапе верификации) — проверяется адекватность модели при помощи статистических критериев по схеме проверки статистических гипотез.

После этого модель используется для прогнозирования или для объяснения внутренних механизмов исследуемых процессов.

Целью математико-статистического моделирования является получение такого инструмента, который позволит глубже проникнуть в суть исследуемого экономического процесса.

Источник

• ← если шоркнул машину и уехал что за это будет
• загорелся чек на автомобиле в чем причина →